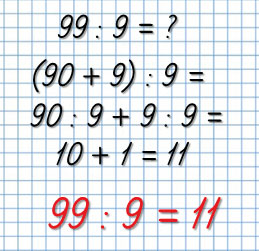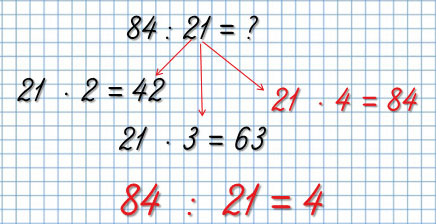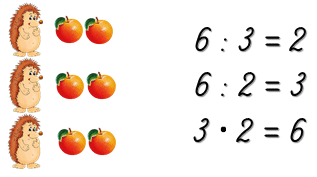Что такое внетабличное деление
Внетабличное деление
Внетабличное деление на однозначное число
В числе 99 – 9 десятков и 9 единиц; делю 9 десятков на 9, получаю 1 десяток, или это число 10; далее делю 9 единиц на 9 и получаю число 1. Теперь к 10 прибавляю 1 и получаю 11. Тогда,
В числе 84 – 8 десятков и 4 единицы; делю 8 десятков на 4, получаю 2 десятка, или это число 20; далее делю 4 единицы на 4 и получаю число 1. Теперь к 20 прибавляю 1 и получаю 21. Тогда,
Нахождение частного подбором
Пробуем в частном 2 и проверяем: 29 • 2 = 58, 58
Пробуем в частном 3 и проверяем: 29 • 3 = 87, 87 = 87, значит, 87 : 29 = 3.
Внетабличное деление на двузначное число
Если ты еще не умеешь решать такие примеры столбиком, то можно решать при помощи умножения.
Деление суммы на число
Чтобы разделить сумму на число, можно вычислить сумму и разделить её на число или разделить на число каждое слагаемое и полученные результаты сложить.
Случай 1:
Рассуждай так:
Нахожу сумму чисел 15 и 25, получаю 40. Теперь 40 делю на 5 и получаю 8.
(15 + 25) : 5 = 40 : 5 = 8
Каждое из слагаемых делю на 5 и результат складываю. Сначала делю первое слагаемое 15 на 5, получу 3, потом на 5 разделю второе слагаемое 25, получу 5, теперь полученные результаты 3 и 5 сложу и получу 8. Запишу так:
(15 + 25) : 5 = 15 : 5 + 25 : 5 = 3 + 5 = 8
Значит, (15 + 25) : 5 = 8
Случай 2:
Число 36 представлю в виде суммы слагаемых, которые легко делятся на 2, например, 20 и 16. Эту сумму надо разделить на 2.
Сначала делю первое слагаемое 20 на 2, получу 10, потом на 2 разделю второе слагаемое 16, получу 8, теперь полученные результаты 10 и 8 сложу и получу 18.
32 : 2 = (20 + 16) : 2 = 20 : 2 + 16 : 2 = 10 + 8 = 18
Поделись с друзьями в социальных сетях:
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
Ребята, ответьте на вопрос. Что находится в начале числовой линейки?
Правильно, нуль. Здравствуйте, ребята! Сегодня на уроке мы отправимся по математическому маршруту, где познакомимся с внетабличным делением и умножением.
В умноженье и деленье!
Примеры внимательно читайте –
Быстро, правильно считайте!
За старанье, прилежание
Цветную ленту получайте!
В конце урока вас ждет яркий сюрприз, но сейчас откройте тетради, возьмите ручки, начинайте выполнять задания.
Умножение и деление круглых чисел
Обратите внимание: круглым называется число, которое оканчивается нулем — 10, 20, 30, 40, 50, 60, 70, 80, 90, 100. Круглые числа похожи на десятки. Разряд единиц круглых десятков равняется нулю.
Прочитайте таблицу круглых чисел:
Умножение и деление круглого двухзначного числа на однозначное выполняется по определенным правилам. Познакомьтесь с этими правилами.
Деление круглых чисел
Рассмотрим пример внетабличного деления:
В примерах деления круглого числа делим количество десятков и дописываем в ответе нуль.
Делим на 10 — убираем в ответе нуль.
В частном не пишем нули, если делимое, делитель — круглые числа.
Умножение круглых чисел
А знаете ли вы, что за тысячелетия развития математики было придумано много вариантов умножения. Считалось, что для овладения искусством вычисление нужен талант. Итальянский математик 15 века Лука Пачоли приводит 8 способов. Познакомимся с некоторыми из них.
Рассмотрите прием внетабличного умножения.
Двадцать умножить на три равно шестидесяти.
Воспользуемся правилом перестановки множителей, получим пример, который умеем решать.
Прочитайте правило внимательно.
При умножении круглого числа на однозначное, надо умножить десятки на второй множитель, в ответ справа добавить нуль.
Увеличить в десять раз — это значит написать в значение произведения первый множитель и добавить к нему 0 справа.
Произведение семи и десяти равно семидесяти.
Воспользуйтесь правилами математики внетабличного умножения и деления для решения примеров:
Проверьте:
Ошибок нет, молодцы. Ваша первая награда — красная ленточка.
Впереди ждут новые открытия, не отставайте, думайте, решайте.
Умножение суммы на число
Задание. Посчитайте и запишите решение на вопрос: сколько квадратов в прямоугольнике?
Вариант 1. Рассуждайте так: в ряду шесть синих квадратов плюс три красных квадрата. Рядов 4. Значит, запишите решение:
Сумма в скобках равна девяти. 9 ∙ 4 = 36. Это табличное умножение.
Вариант 2. Количество квадратов подсчитайте другим способом. Узнайте, сколько синих, потом, сколько красных, полученные результаты сложите.
Таким способом удобно умножать большие величины.
Любое двузначное число легко записать как сумму разрядных слагаемых: круглых десятков и единиц.
Умножайте сначала десятки, потом единицы, произведения складывайте.
Как это сделать, рассмотрите на примере.
Сумму десяти и пяти умножим на шесть.
Это распределительное свойство умножения суммы на число.
Правило умножения суммы на число запишите буквенным выражением.
За внимание награждаю вас оранжевой лентой.
Идите по маршруту дальше.
Умножение двузначного числа на однозначное
Сейчас будем решать вот такие примеры:
Они такие легкие, что мы разделаемся с ними на раз, два, три.
Устное умножение чисел двузначного на однозначное
Считать устно — это просто замечательно, я сам стараюсь обходиться без калькулятора. Но для того, чтобы это делать, нужно знать приемы устного счета. Это чудесная разминка для мозга.
Мы разберемся с примерами, когда двузначное число умножается на однозначное. Вы научились записывать сумму разрядных слагаемых, поэтому воспользуемся этим умением.
Давайте тренироваться:
Пример сложнее.
89 умножить на семь.
Ну как, простые примеры? По способу решения — да. А вот, если не знаете таблицу умножения, то не такие уж простые.
Умножение столбиком двузначного числа на однозначное
Это письменный прием вычислений. Такие примеры мы привыкли называть примеры в столбик или примеры столбиком. Давайте научимся правильно записывать такое решение.
Пусть надо 58 умножить на семь.
А теперь начните решать. Последовательно умножьте слева направо все цифры первого множителя на 7, пока они не закончатся. Умножаем 8 на 7, это 56. Что нам с ним делать? Смотрите, то, что единицы, мы так и записываем.
Процесс умножения закончен. Читаем ответ — четыреста шесть.
Давайте посмотрим другой пример.
Проверьте, как записали.
Выполните вычисления. 5 ∙ 9 = 45. Пять записываем под девяткой. Четыре в уме.
4 ∙ 9 = 36. Да 4 в уме. 36 + 4 = 40. Записываем значение произведения. Читаем ответ — 405.
Проверьте свою запись.
Деление суммы на число
Прочитайте рассказ «Из истории символов».
Люди сначала умножали, делить научились позднее. В десятом веке ученый Герберт в математических трудах упомянул сложные правила «железного деления». Старинная итальянская поговорка гласила: «Трудное дело — деление». Оно и в самом деле было трудно, если принять во внимание утомительные методы, какими выполнялось тогда это действие.
В середине 18 века в странах Европы начали делить привычным для нас простым способом, который изобрели арабы. Он получил название «золотое деление».
Для записи действия применяются разные знаки:
В 17 веке в Англии и США чаще всего использовался обелюс. Символ в виде двух точек придумал немецкий математик Г. Лейбниц в 1684 году. На письме он очень похож на двоеточие.
Познакомимся со способом деления. Выполните задание.
Какие числа нужно вставить в «окошки», чтобы получились верные равенства?
Решение.
Рассуждаем: первое слагаемое — круглое число. В окошко нужно подставить слагаемое, которое делится на три без остатка.
Подсказка: вспомните результаты табличного умножения на 3. Например, 27.
Деление суммы чисел 30 и 27 на данное число 3 вычисляется так: каждое слагаемое делится на три и результаты складываются.
Запишите подробное решение:
Сформулируйте правило деления суммы на число:
Деление двузначного числа на однозначное
Ребята, вы меня узнали? Люблю наряжаться на маскарад. Вот прицепил такие усы, думал, что буду похож на фокусника. Чудеса начинаются.
Такие задания называют примерами с «усиками». Да, да, но усики носят не люди, кто делит, а сами примеры. Рисовать их нужно простым карандашом, а когда научитесь быстро считать, то просто представляйте в голове.
Устное деление двузначного на однозначное
Задание 1.
Пусть надо решить, сколько будет
К «усикам» запишем такие два слагаемых, которые делятся на 8, а в сумме дают 96.
Самое главное — это не ошибиться в подборе первого «усика». Надо запомнить, что он всегда больше, чем второй. Ищем его, умножая 8 на 10. Если не подойдет, то будем умножать на 20, на 30. Главное, чтобы было круглое число.
Все понятно? Будем тренироваться.
Задание 2.
Задание 3.
Попробуем разделить 90 на два. «Первый усик» явно не 20, тогда второй будет 70. Знаем, что «второй усик» не может быть больше первого.
Вижу, что не 60, потому что 30 разделить на два — это не табличный случай.
Следовательно, 2 ∙ 40 = 80. Значит «первый усик» предположительно 80. «Второй усик» тогда найдем вычитанием: 90 – 80 = 10. Десять разделить на два, это таблица.
Как думаете, вы справитесь с делением? Когда встречаете случаи, где двузначное число делится на однозначное, и примеры не относятся к таблице умножения, то решайте подбором «усиков». Разбивайте делимое на подходящие слагаемые. Их можно записать суммой в скобочках, а при делении использовать правило деления суммы на число.
Решите задачу.
Таня выполнила 96 примеров, а Коля в 4 раза меньше. Сколько примеров решил Коля?
Чтобы ответить на вопрос задачи, надо выполнить действие деления.
«Усиками» будут 80 и 16, получается сумма 80 + 16. Значит, каждое из этих слагаемых разделите на 4, а частные сложите.
Ответ: 24
Деление столбиком двузначное на однозначное
Письменное деление уголком просто невозможно усвоить без блестящего знания таблицы умножения. Это просто трата времени и нервов. В древности в римских школах ее заучивали хором на распев. Знаете ответы на «отлично», тогда переходите на примеры деления в столбик.
Задание 1.
Пусть надо 84 разделить на три. Посмотрите на запись. Такой значок означает деление уголком. Уголок имеет наверху делитель, на который делим. Под чертой — результат, который ищем. Он называется частным.
Нам надо узнать, чему равно частное. Но прежде определим, сколько цифр будет в результате. Это очень важный шаг, поэтому упускать его нельзя. Как мы будем это делать? Посмотрите на первую цифру. Это восьмерка. Восемь больше трех. Значит, она может дать нам полноценную цифру в частном. Ставим точку. После восьмерки еще одна цифра, это значит, что частное — двузначное число. Под чертой в уголке карандашом поставьте вторую точку.
Первое неполное делимое — восьмерка. Начинаем ее делить на три, ищем табличный случай. Легче всего уменьшать 8 на единицу.
8 – 1 = 7. В таблице нет деления семи на три.
Уменьшаем еще на 1.
7 – 1 = 6. Шесть делится на три, получается — по два. Записываем 2 в частное под чертой.
Теперь мы должны понять, сколько не разделили. Ведь разделили всего шесть.
А надо было разделить восемь.
Два осталось неразделенным. Это остаток. Он должен быть меньше делителя.
Давайте проверим: два меньше трех.
Да, действительно. Мы сделали все правильно. Этот шаг очень важен. Не забывайте сравнивать остаток с делителем.
После этого сносим следующую цифру с тем, чтобы получить новое неполное делимое. Обратите внимание: нужно писать каждую цифру в своей клетке. Получается неполное делимое 24.
Ответ: 28.
Задание 2.
Решите пример столбиком 96 : 4 =
Проверьте:
Ура! Наш математический маршрут пройден. Знания-сокровища из цветных лент превратились в волшебную радугу. Что же у нас вышло, что мы унесем в нашем сундуке. Закончите предложения:
Урок по математике на тему «Внетабличное деление»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику


«Шахтинский педагогический колледж»
Технологическая карта (план-конспект)
проведенного в 3 «А» классе
гимназии им. А. С. Пушкина
студентом группы 3 «А»
Дреевым Дмитрием Александровичем
Дата проведения: 26.01.2016 г.
Учитель: Астраханцева Т. В.
Преподаватель-руководитель практики: Васильченко З. Н.
Класс 3 «А» ФИО практиканта Дреев Дмитрий Александрович
Технологическая карта урока № 2
-Продолжить изучать внетабличное деление;
-Формировать устную и письменную математическую речь у учащихся;
-Развивать монологическую речь.
1.Закрепление умения использовать приём деления двузначного числа на однозначное число и проконтролировать уровень усвоения.
2.Закрепление умения решать задачи изученных видов;
3.Развивитие процессов: логического мышления, воображения, восприятия, умения применять логические операции (анализ, синтез, классификация, сравнение, обобщение), наблюдательности и математической речи;
4.Формирование умения реально оценивать свои возможности на каждом этапе урока и на уроке в целом.
1.Формирование проявления устойчивого познавательного интереса к математическому содержанию учебной деятельности при разбиении многозначных чисел на разрядные слагаемые; деление двузначного на однозначное в строчку;
2.Формирование понимания как результата причин успеха в учебной деятельности при разбиении многозначных чисел на разрядные слагаемые; делении двузначного на однозначное в строчку;
3.Оценивание собственной учебной деятельности по критериям определенным совместно с учителем при разбиении многозначных чисел на разрядные слагаемые; умножении и делении двузначного на однозначное в строчку;
1.Умение планировать и регулировать свою деятельность.
2.Умение самостоятельно планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач.
3.Умение соотносить свои действия с планируемыми результатами
4.Умение прогнозировать результаты и уровень усвоения по ранее определенному плану;
5.Умение контролировать выполнение по образцу;
1.Умение получать необходимую информацию, отстаивать свою точку зрения в диалоге и в выступлении, 2.Умение донести свою позицию до других;
3. П остроение учебного сотрудничества при взаимодействии с одноклассниками и учителем в процессе изучения учебной темы;
4.Умение задавать вопросы при изучении внетабличного деления.
1.Умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя;
2.Умение добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке;
3.Умение структурировать знания при выполнении внетабличного деления и умножения;
4.Умение осознанно и произвольно строить речевые высказывания в устной и письменной форме при устанавливании связи деления.
Урок повторения и формирования УУД.
Формы, приёмы и методы
Словесный, наглядный, практический, логический.
Учебник, тетрадь, доска, мел, ТСО (компьютер, проектор, презентация, разработанная учителем)
1. Организация начала урока.1-3 мин.
2. Актуализация знаний.10 мин.
3. Постановка проблемы.10-15 мин.
4. Физминутка 3-5 мин.
5. «Открытие» детьми новых знаний.10-15мин..
6. Итог урока. Рефлексия.3-5 мин.
1. Организация начала урока
Здравствуйте, ребята. Меня зовут Дмитрий Александрович и урок математики сегодня проведу у вас я. Садитесь. Проверили готовность к уроку (на парте всё необходимое).
Начнем урок с устного счета.
14- первый множитель, 3 – второй. Найдите произведение (42)
Найдите сумму чисел: 46 и 47 (93)
Во сколько раз 560 больше 8? (в 70 раз)
468 уменьшить на 400 (68)
Во сколько раз 60 меньше 600? (в 10 раз)
Произведение чисел 8 и 10 (80) (почему?)
Делимое 100, делитель 2. Чему равно значение частного? (50) (почему?)
Делимое 66, делитель 6. Чему равно значение частного? (11)
Первый множитель – 15, второй множитель – 5, найдите произведение (75)
Хорошо, ребята. Вы показали, что
Работа в тетрадях: Откройте тетради, запишите число, классная работа. Сейчас мы выполним задание номер 257 на странице 5. Кто может прочитать?
— Выполни деление, сделав подробную запись.
226:2, мы можем число 226 представить в виде суммы разрядных слагаемых, потом каждое слагаемое делим по отдельности и результаты складываем
226:2= (220+20+6):2= 220:2+20:2+6:2= 110+10+3=123
609:3, мы можем число 609 представить в виде суммы разрядных слагаемых, потом каждое слагаемое делим по отдельности и результаты складываем
609:3=(600+9):3= 600:3+9:3= 200+3= 203
884:4, мы можем число 884 представить в виде суммы разрядных слагаемых, потом каждое слагаемое делим по отдельности и результаты складываем
884:4= (800+80+4):4= 800:4+80:4+4:4= 200+20+1= 221
486:2, мы можем число 486 представить в виде суммы разрядных слагаемых, потом каждое слагаемое делим по отдельности и результаты складываем
486:2= (400+80+6):2= 400:2+80:2+6:2=200+40+3=243
909:3, мы можем число 909 представить в виде суммы разрядных слагаемых, потом каждое слагаемое делим по отдельности и результаты складываем
909:3= (900+9):3= 900:3+9:3=300+3=303
804:4, мы можем число 804 представить в виде суммы разрядных слагаемых, потом каждое слагаемое делим по отдельности и результаты складываем
804:4= (800+4):4= 800:4+4:4= 200+1=201
Молодцы, ребята. Вы научились делить трехзначные числа на однозначное, представляя число в виде суммы разрядных слагаемых
— Назовите равенства таблицы умножения, которые использованы при вычислении частных 609:3 и 486:2
(При вычислении частного 609:3 использованы равенства таблицы умножения 6:3=2 и 9:3=3
(При вычислении частного 486:2 использованы равенства таблицы умножения 4:2=2, 8:2=4 и 6:2=3).
-Хорошо, переходим к заданию 3.
— Запишите другие произведения и частные, значения которых можно найти с помощью равенства пункта 2.
609:3 можно записать с помощью равенства 3∙203=609; 203∙3=609; 609:203=3
486:2=243, можно записать с помощью равенства 243∙2=486; 2∙243=486; 486:243=2.
Хорошо. Сколько выражений мы составили, имея равенства 609:3=203 (мы составили 3 выражения, имея равенство 609:3=203)
-Сколько выражений мы составили, имея равенства 486:2=243 (мы составили 3 выражения, имея равенство 486:2=243)
-Еще раз назовите их.
«3. Постановка проблемы.
Сейчас выполним номер 259, кто прочитает задание 1?
— Сравни произведения 32∙2 и 36∙6
32∙2 меньше 36∙2, так как 32∙2= 64, а 36∙2= 72
-Хорошо. Поднимите руку, кто может выполнить подробную запись?
32∙2= (30+2)∙2=30∙2+2∙2= 60+4=64
36∙2= (30+6)∙2=30∙2+6∙2= 60+12=72
— Ребята, сравните свои записи. Какая между ними разница? (Разница в том, что первом случае 2∙2 нет перехода через разряд, а во втором 6∙2=12- есть переход через разряд).
-Какие цифры можно поставить в числе 3*, чтобы при умножении на 2 не было перехода через разряд? (Чтобы при умножении на число 2 не было перехода через разряд, можно поставить цифры1, 2, 3, 4)
-Ребята, запишите все произведения, чтобы при умножении на число 2 не было перехода через разряд. (31∙2=62 32∙2=64 33∙2=66 34∙2=68)
-Молодцы. Сейчас выполним физминутку.
Для начала мы с тобой
Для начала мы с тобой
Крутим только головой.
Корпусом вращаем тоже.
Это мы, конечно, сможем.
(Повороты вправо и влево.)
(Потягивания вверх и в стороны.)
От разминки поскраснели
И за парты снова сели.
(Дети садятся за парты.)
5. «Открытие» детьми новых знаний.
Теперь решим задачу номер 260. Доминика будет читать задачу, вы все внимательно следите, слушайте и поймите её содержание?
Ящик с деталями имеет массу 99 кг, а 8 таких же пустых ящиков имеют массу 25 кг. Во сколько раз масса пустого ящика легче массы ящика с деталями?
— Сейчас прочитайте задачу про себя и приготовьтесь отвечать на мои вопросы
-О чем эта задача? (Эта задача о ящиках с деталями и о пустых ящиках)
-Какую массу имеет ящик с деталями? (Ящик с деталями имеет массу 99 кг)
-Какую массу имеют 8 таких же пустых ящика? (8 таких же пустых ящика имеют массу 24 кг)
— Каков вопрос задачи? (Во сколько раз пустой ящик легче ящика с деталями?)
— Можем мы ответить на вопрос задачи? (Нет, не можем, так как мы знаем, что ящик с деталями имеет массу 99 кг, но не знаем сколько кг весит пустой ящик)
-Можем ли мы найти массу одного пустого ящика? (можем, выполнив действие 24:8)
— Ребята, а теперь мы можем узнать во сколько раз пустой ящик легче ящика с деталями? (Да, мы можем узнать во сколько пустой ящик легче ящика с деталями, так как мы знаем, что ящик с деталями весит 99 кг, а пустой ящик весит 3 кг, для этого мы выполним действие 99:3)
-Теперь мы можем записать решение задачи? (да, можем, так как мы ответили на вопрос задачи.
Запись решения задачи.
-Кто может пойти выполнить краткую запись задачи и записать решение?
Деление
В этом разделе познакомимся с делением и узнаем, что деление – это математическая операция, обратная умножению.
Умножение – это последовательное сложение чисел, а деление – это последовательное вычитание чисел.
Как ёжикам поделить между собой яблоки поровну?
Нужно воспользоваться действием деления и узнать, сколько раз по 3 содержится в 6.
Любой пример на умножение можно представить двумя примерами на деление.
Например, для выражения 6 • 4 = 24 есть два обратных выражения:
24 : 4 = 6 — нужно из 24 вычесть число 4 ровно 6 раз.
24 : 6 = 4 — нужно из 24 вычесть число 6 ровно 4 раз.
Числа при делении
При делении, как и при другом математическом действии, каждое число имеет свое название.
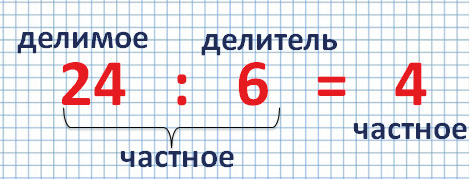
Число, которое делят, называется делимое.
Число, на которое делят, называется делитель.
Результат деления называется частное.
Чтение числовых выражений
Этот пример можно прочитать по-разному.
Деление на 1
Деление на 0
Деление числа само на себя
Связь деления и умножения
Чётные и нечётные числа
Числа, которые делятся на 2 без остатка, называются чётными, а числа, которые не делятся на 2 без остатка, называются нечётными.
Чётные: 6, 22 44, 60, 74, 82, 96
Нечётные: 7, 13, 21, 37, 45, 97
В несколько раз меньше
Для примера решим задачу:
В магазине было 8 котят, а лисичек в 4 раза меньше. Сколько было лисичек?
Значит, чтобы узнать, сколько было лисичек, нужно 8 : 4 = 2 (л.)
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях: