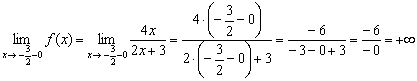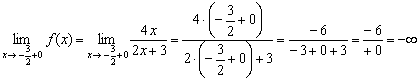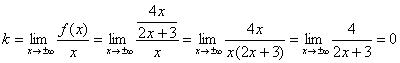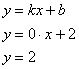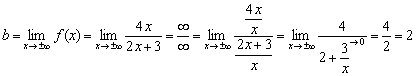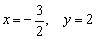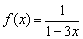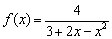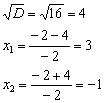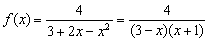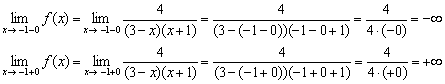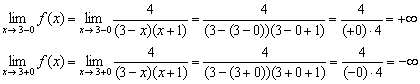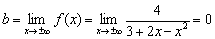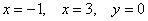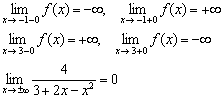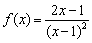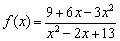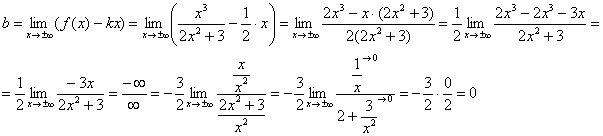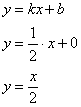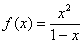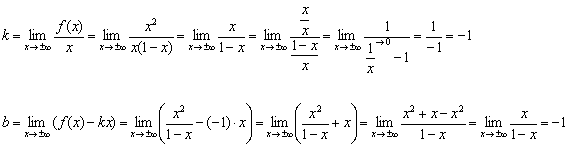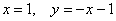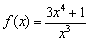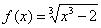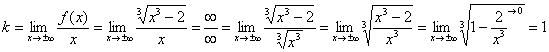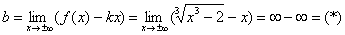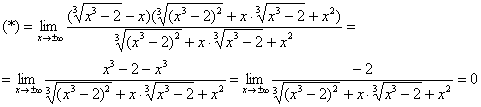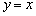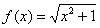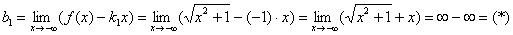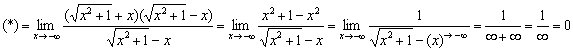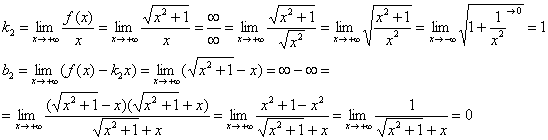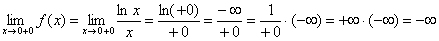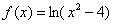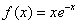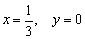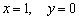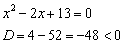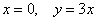Что такое вертикальная асимптота

Асимптота графика функции: определение, как искать

Что такое асимптота — понятие и определение

Асимптота графика функции у=f (x) представляет собой прямую L, максимально приближающеюся к графику функции, точка которого стремится к бесконечности, то есть неограниченно удаляется от начала координат по кривой. Расстояние между этой точкой функции у=f(x) и асимптотой L стремится к нулю.

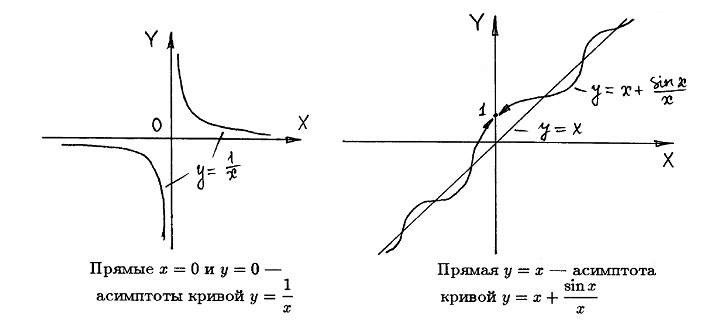
На рисунке приведены примеры асимптот графиков функций.

На рисунке слева продемонстрирована кривая, которая приближается к асимптоте и остается с одной стороны по отношению к ней.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

На рисунке справа представлена кривая (график функции), которая пресекает асимптоту бесконечное множество раз с разных сторон

Асимптоты графика функции, основные виды

Асимптоты делятся на три вида: вертикальные, наклонные и горизонтальные.

У разных функции в наличии может быть различное количество асимптот:

Приведем пример нахождения асимптот гиперболы.

Гипербола — геометрическое место расположения точек, от которых абсолютная величина разности растояний до двух фокусов (заданных точек), является постоянной и меньшей, чем расстояние между самими фокусами.

Это действительно, так как:

Следовательно, если абсцисса х неограниченно возрастает, то график гиперболы и ее асимптота неограниченно сближаются.

Расположение асимптот гиперболы соответствует диагоналям прямоугольника, стороны которого параллельны оси Ох и оси Оу, а центром служит начало координат.

Пример

Необходимо составить уравнение гиперболы, если следующие уравнения задают ее асимптоты:

Решение

Применим формулу \(y=\frac bax\) и получим:

Подставим координаты точки М в общую формулу уравнения гиперболы:

Получим систему уравнений. Чтобы получить уравнение данной гиперболы, необходимо вычислить полученную систему уравнений.

Вертикальные асимптоты

Если хотя бы один из пределов \(\lim_f(x)\) или \(\lim_f(x)\) является равным +∞ или —∞, то вертикальной асимптотой графика функции у=f(x) будет являться прямая х=с.

Примеры вертикальных асимптот:

Пример 1

Необходимо определить вертикальную асимптоту функции \(\lim_a(x)=0.\)

Решение

то x=0 — вертикальная асимптота.

Пример 2

Ось ординат является вертикальной асимптотой, так как

Наклонные асимптоты

Если в определении асимптоты присутствует +∞ или —∞, то она относится либо к горизонтальной, либо к наклонной.

Если k=0, то наклонная асимптота превращается в горизонтальную.

Применение правила Лопиталя

Правило Лопиталя применяется, когда границы не определены, например, 0/0 или ∞/∞:

Если функции можно дифференцировать, и они относятся к окрестностям точки x=a, тогда наклонную асимптоту необходимо искать по формуле:

Производная может применяться многократно для получения константы в числителе или знаменателе.

Пример 1

Прямая у=х — наклонная асимптота графика данной функции.

Пример 2

Рассмотрим два варианта:

То есть правая ветвь кривой имеет наклонную асимптоту в виде прямой у=х-2.

То есть левая ветвь кривой имеет наклонную асимптоту в виде прямой у=-х+2.

Горизонтальные асимптоты

Прямая y=b является горизонтальной асимптотой для графика функции y=f(x), если

Пример 1

Имеется функция: \(y=4+\frac1x.\)

поэтому y=4 — горизонтальная асимптота данной функции.

Пример 2

Значит, у=1 — горизонтальная асимптота графика функции.

Пример 3

Источник

Асимптоты

Вертикальная асимптота.

Если выполнено хотя бы одно из условий
$$
\lim_-0>f(x)=\infty,\qquad\lim_+0>f(x)=\infty,\nonumber
$$
то прямую \(x=x_<0>\) называют вертикальной асимптотой графика функции \(y=f(x)\).

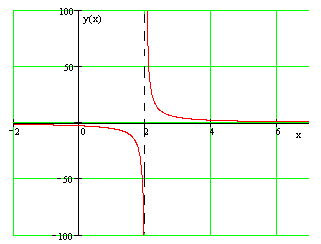
Например, прямая \(x=0\) — вертикальная асимптота графиков функций \(y=\displaystyle \frac<1>\), \(y=\operatornamex^2\), \(y=\displaystyle \frac<1>>\), \(y=\operatornamex\), прямая \(x=-1\) — вертикальная асимптота графика функции \(y=\displaystyle \frac<3-2x>\), прямые \(x=\displaystyle \frac<\pi> <2>+\pi k\ (k\in \mathbb)\) — вертикальные асимптоты графика функции \(y=\operatornamex\).

Функции и их асимптоты

Асимптота	Функция	График функции
\(x=0\)	\(y=\displaystyle \frac<1>\)
	\(y=\operatornamex^2\)
	\(y=\displaystyle \frac<1>>\)
	\(y=\operatornamex\)
\(x=-1\)	\(y=\displaystyle \frac<3-2x>\)

Асимптота (невертикальная асимптота).

Прямую
$$
y=kx+b\nonumber
$$
называют асимптотой (невертикальной асимптотой) графика функции \(y=f(x)\) при \( x\rightarrow+\infty\), если
$$
\lim_(f(x)-(kx+b))=0.\label
$$
Если \(k\neq 0\), то асимптоту называют наклонной, а если \(k=0\), то асимптоту \(y=b\) называют горизонтальной.

Аналогично вводится понятие асимптоты при \(x\rightarrow-\infty\).

Функции и их асимптоты

Асимптота	Функция	График функции
\(y=1\)	\(y=e^<1>\)
	\(y=\operatorname	x\)
	\(y=\operatornamex\)
\(y=\displaystyle \frac<\pi><2>\)	\(y=\operatornamex\)
\(y=\pi\)	\(y=\operatornamex\)

Найти асимптоту при \(x\rightarrow+\infty\) и \(x\rightarrow-\infty\) графика функции:

Для того, чтобы прямая \(y=kx+b\) была асимптотой графика функции \(y=f(x)\) при \( x\rightarrow+\infty\), необходимо и достаточно, чтобы существовали конечные пределы
$$
\lim_\frac=k,\label
$$
$$
\displaystyle \lim_(f(x)-kx)=b.\label
$$

\(\circ\) Необходимость. Если прямая \(y=kx+b\) — асимптота графика функции \(y=f(x)\) при \(x\rightarrow+\infty\), то выполняется условие \eqref или равносильное ему условие
$$
f(x)=kx+b+\alpha(x),\quad \alpha(x)\rightarrow 0 \quad при \quad x\rightarrow +\infty.\label
$$
Разделив обе части равенства \eqref на \(x\), получим
$$
\frac=k+\frac+\frac<\alpha(x)>,\nonumber
$$
откуда следует, что существует предел \eqref.

Из равенства \eqref получаем
$$
f(x)-kx=b++\alpha(x),\ где \ \alpha(x)\rightarrow 0 \ при \ x\rightarrow+\infty,\nonumber
$$
откуда следует, что существует предел \eqref.

Для случая горизонтальной асимптоты данная теорема формулируется в следующем виде: для того, чтобы прямая \(y=b\) была асимптотой графика функции \(y=f(x)\) при \(x\rightarrow+\infty\), необходимо и достаточно, чтобы \(\displaystyle \lim_f(x)=b\).

Источник

Асимптоты графика функции

Вы будете перенаправлены на Автор24

Достаточно часто на практике приходится иметь дело с функциями, которые определены не на всей числовой прямой, либо принимают не любые значения из множества действительных чисел.

В таких случаях при построении графиков функций получаем, что график функции не является непрерывной линией, а имеет некоторые разрывы. В результате чего становится целесообразным ввести понятие «асимптота».

Среди асимптот выделяют следующие виды:

Отметим, что асимптоты на графике функции изображаются пунктирной линией.

Готовые работы на аналогичную тему

График функции может иметь только правую либо только левую горизонтальную асимптоту.

Условия существования наклонной асимптоты определяются следующей теоремой.

Наклонная асимптота может быть левой (график приближается справа), правой (график приближается слева) или двусторонней (график приближается с обоих сторон).

Следовательно, график данной функции не имеет наклонной асимптоты.

График функции может иметь одновременно несколько асимптот, например, вертикальную и наклонную.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 17 02 2021

Источник

Слово асимптота происходит от Греческий ἀσύμπτωτος (Asumptōtos), что означает «не падают вместе», от ἀ приват. + σύν «вместе» + πτωτ-ός «упавший». [3] Термин был введен Аполлоний Пергский в своей работе над конические секции, но, в отличие от современного значения, он использовал его для обозначения любой линии, которая не пересекает данную кривую. [4]

Содержание

Вступление

Асимптоты функций

Вертикальные асимптоты

Линия Икс = а это вертикальная асимптота графика функции у = ƒ(Икс) если верно хотя бы одно из следующих утверждений:

а кривая имеет вертикальную асимптоту Икс=1.

Функция ƒ(Икс) может или не может быть определено в а, и его точное значение в точке Икс = а не влияет на асимптоту. Например, для функции

Если функция имеет вертикальную асимптоту, то не обязательно, чтобы производная функции имела вертикальную асимптоту в том же месте. Примером является

Для последовательности точек

Горизонтальные асимптоты

В первом случае ƒ(Икс) имеет у = c как асимптота, когда Икс стремится к −∞, а во втором ƒ(Икс) имеет у = c как асимптота при Икс стремится к + ∞

Например, функция арктангенса удовлетворяет

У функций могут отсутствовать горизонтальные асимптоты с одной или обеих сторон, либо может быть одна горизонтальная асимптота, одинаковая в обоих направлениях. Например, функция ƒ (Икс) = 1/(Икс 2 +1) имеет горизонтальную асимптоту при у = 0, когда Икс стремится как к −∞, так и к + ∞, поскольку, соответственно,

Наклонные асимптоты

Когда линейная асимптота не параллельна Икс— или же уось, она называется наклонная асимптота или же наклонная асимптота. Функция ж(Икс) асимптотична прямой у = mx + п (м ≠ 0) если

В первом случае строка у = mx + п наклонная асимптота ƒ(Икс) когда Икс стремится к + ∞, и во втором случае прямая у = mx + п наклонная асимптота ƒ (х) когда Икс стремится к −∞.

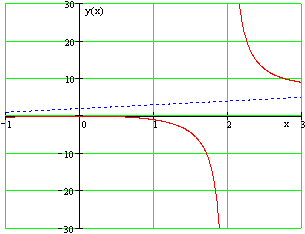
Пример: ƒ (Икс) = Икс + 1/Икс, имеющий наклонную асимптоту у = Икс (то есть м = 1, п = 0), как видно из пределов

Элементарные методы определения асимптот

Асимптоты многих элементарных функций можно найти без явного использования пределов (хотя при выводе таких методов обычно используются пределы).

Общее вычисление наклонных асимптот для функций

Наклонная асимптота для функции ж(Икс), будет задаваться уравнением у=mx+п. Значение для м вычисляется первым и определяется как

м = def Lim Икс → а ж ( Икс ) / Икс > <=>> lim _ f (x) / x>

Имея м тогда значение для п можно вычислить

куда а должно быть то же значение, что и раньше. Если этот предел не существует, то в этом направлении нет наклонной асимптоты, даже если предел, определяющий м существовать. Иначе у = mx + п наклонная асимптота ƒ(Икс) в качестве Икс как правило а.

Например, функция ƒ(Икс) = (2Икс 2 + 3Икс + 1)/Икс имеет

так что у = 2Икс + 3 асимптота ƒ(Икс) когда Икс стремится к + ∞.

Функция ƒ(Икс) = ln Икс имеет

Так у = ln Икс не имеет асимптоты, когда Икс стремится к + ∞.

Асимптоты для рациональных функций

А рациональная функция имеет не более одной горизонтальной асимптоты или наклонной (наклонной) асимптоты и, возможно, много вертикальных асимптот.

Вертикальные асимптоты возникают только тогда, когда знаменатель равен нулю (если и числитель, и знаменатель равны нулю, сравниваются кратности нуля). Например, следующая функция имеет вертикальные асимптоты в Икс = 0 и Икс = 1, но не при Икс = 2.

Наклонные асимптоты рациональных функций

показано справа. В качестве значения Икс увеличивается, ж приближается к асимптоте у = Икс. Это потому, что другой член, 1 / (Икс+1), приближается к 0.

Если степень числителя более чем на 1 больше степени знаменателя, а знаменатель не делит числитель, будет ненулевой остаток, который стремится к нулю как Икс увеличивается, но частное не будет линейным, и функция не имеет наклонной асимптоты.

Преобразования известных функций

Если известная функция имеет асимптоту (например, у= 0 для ж(х) =е Икс ), то его переводы также имеют асимптоту.

Если известная функция имеет асимптоту, то масштабирование функции также имеют асимптоту.

Например, ж(Икс)=е Икс-1 +2 имеет горизонтальную асимптоту у= 0 + 2 = 2, и никаких вертикальных или наклонных асимптот.

Общее определение

Позволять А : (а,б) → р 2 быть параметрический плоская кривая в координатах А(т) = (Икс(т),у(т)). Предположим, что кривая стремится к бесконечности, то есть:

если γ (т) является изменением параметризации, то расстояние становится равным

которое стремится к нулю одновременно с предыдущим выражением.

Эту параметризацию следует рассматривать на открытых интервалах (а,б), куда а может быть −∞ и б может быть + ∞.

Криволинейные асимптоты

Асимптоты и построение кривых

Асимптоты используются в процедурах построение кривых. Асимптота служит ориентиром, показывающим поведение кривой к бесконечности. [10] Для лучшего приближения кривой также использовались криволинейные асимптоты. [11] хотя термин асимптотическая кривая кажется предпочтительным. [12]

Алгебраические кривые

Асимптоты алгебраическая кривая в аффинная плоскость являются касательными к проекционная кривая через точка в бесконечности. [13] Например, можно идентифицировать асимптоты к единичной гиперболе таким образом. Асимптоты часто рассматриваются только для реальных кривых, [14] хотя они также имеют смысл при таком определении для кривых над произвольным поле. [15]

Плоская кривая степени п пересекает свою асимптоту не более чем в точке п−2 другие точки на Теорема Безу, так как пересечение на бесконечности имеет кратность не менее двух. Для конический, есть пара прямых, не пересекающих конику ни в одной комплексной точке: это две асимптоты коники.

Плоская алгебраическая кривая определяется уравнением вида п(Икс,у) = 0 где п является многочленом степени п

Асимптотический конус

имеет две асимптоты

Уравнение для объединения этих двух прямых имеет вид

говорят, что имеет асимптотический конус [16] [17]

Расстояние между гиперболоидом и конусом приближается к 0, когда расстояние от начала координат приближается к бесконечности.

Источник

Как найти асимптоты графика функции?

Именно так формулируется типовое задание, и оно предполагает нахождение ВСЕХ асимптот графика (вертикальных, наклонных/горизонтальных). Хотя, если быть более точным в постановке вопроса – речь идёт об исследовании на наличие асимптот (ведь таковых может и вовсе не оказаться).

Начнём с чего-нибудь простого:

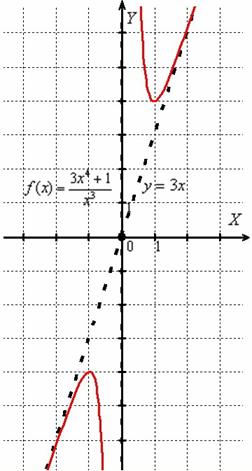
Найти асимптоты графика функции

Решение удобно разбить на два пункта:

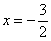
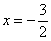
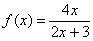
1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при , и сразу понятно, что в данной точке функция терпит бесконечный разрыв, а прямая, заданная уравнением , является вертикальной асимптотой графика функции . Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:

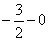
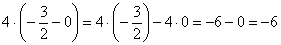
Напоминаю технику вычислений, на которой я подобно останавливался в статье непрерывность функции. Точки разрыва. В выражение под знаком предела вместо «икса» подставляем . В числителе ничего интересного:
.

А вот в знаменателе получается бесконечно малое отрицательное число:
, оно и определяет судьбу предела.

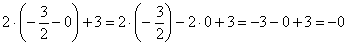
Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого – они ПОМОГАЮТ ПОНЯТЬ, КАК расположен график функции и построить его КОРРЕКТНО. Поэтому обязательно вычислим и правосторонний предел:

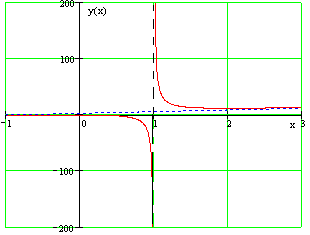
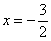
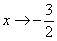
Вывод: односторонние пределы бесконечны, значит, прямая является вертикальной асимптотой графика функции при .

2) Проверим наличие наклонных асимптот:

Первый предел конечен, значит, необходимо «продолжить разговор» и найти второй предел:

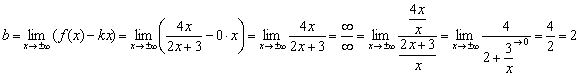
Второй предел тоже конечен.

Таким образом, наша асимптота:

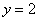
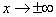
Вывод: прямая, заданная уравнением является горизонтальной асимптотой графика функции при .

Для нахождения горизонтальной асимптоты можно пользоваться упрощенной формулой:

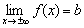
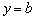
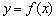
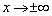
Если существует конечный предел , то прямая является горизонтальной асимптотой графика функции при .

Нетрудно заметить, что числитель и знаменатель функции 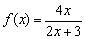одного порядка роста, а значит, искомый предел будет конечным:

Ответ:

По условию не нужно выполнять чертёж, но если в самом разгаре исследование функции, то на черновике сразу же делаем набросок: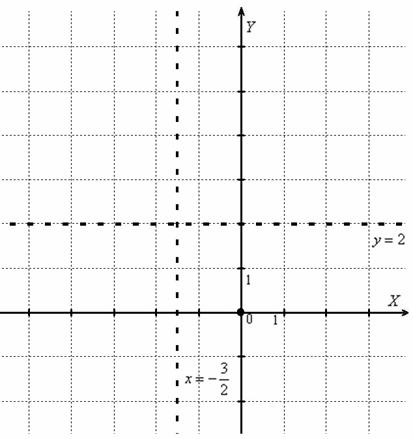

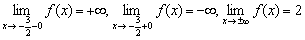
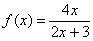
Исходя из трёх найденных пределов , попытайтесь самостоятельно прикинуть, как может располагаться график функции . Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции, и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.

Найти асимптоты графика функции

Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта – вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдёна по упрощенной схеме.

На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:

Найти асимптоты графика функции

Решение: Раз, два и готово:

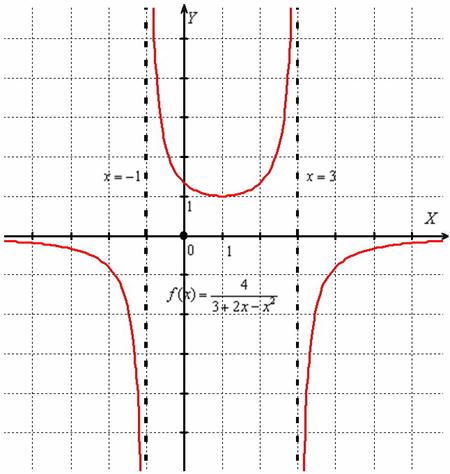
1) Вертикальные асимптоты находятся в точках бесконечного разрыва, поэтому нужно проверить, обращается ли знаменатель в ноль. Решим квадратное уравнение:

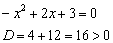
Дискриминант положителен, поэтому уравнение имеет два действительных корня, и работы значительно прибавляется =)

В целях дальнейшего нахождения односторонних пределов квадратный трёхчлен удобно разложить на множители:
(для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.

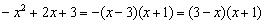
Перепишем функцию в виде

Найдём односторонние пределы в точке :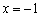

И в точке :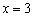

Таким образом, прямые 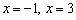являются вертикальными асимптотами графика рассматриваемой функции.

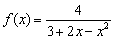
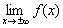
2) Если посмотреть на функцию , то совершенно очевидно, что предел будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:

Таким образом, прямая 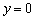(ось абсцисс) является горизонтальной асимптотой графика данной функции.

Ответ:

Найденные пределы и асимптоты дают немало информации о графике функции. Постарайтесь мысленно представить чертёж с учётом следующих фактов:

Схематично изобразите вашу версию графика на черновике.

Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции. Правильная картинка – в конце урока.

Найти асимптоты графика функции

Найти асимптоты графика функции

Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:

Найти асимптоты графика функции

Решение: классика жанра:

1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют. …Хорошо ли это? Не то слово – отлично! Пункт №1 закрыт.

2) Проверим наличие наклонных асимптот:

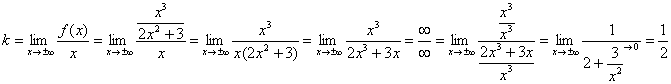
Первый предел конечен, поэтому едем дальше. В ходе вычисления второго предела для устранения неопределённости «бесконечность минус бесконечность» приводим выражение к общему знаменателю:

Второй предел тоже конечен, следовательно, у графика рассматриваемой функции существует наклонная асимптота:

Вывод:

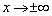
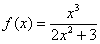
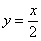
Таким образом, при график функции бесконечно близко приближается к прямой :

Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы – важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).

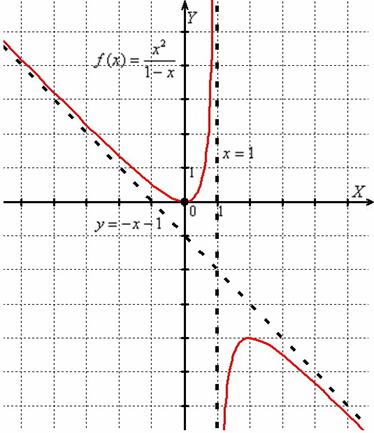
Найти асимптоты графика функции

Решение: комментировать особо нечего, поэтому оформлю примерный образец чистового решения:

1) Вертикальные асимптоты. Исследуем точку .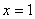

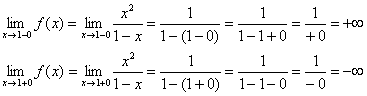
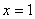
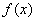
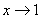
Прямая является вертикальной асимптотой для графика при .

2) Наклонные асимптоты:

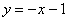
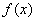
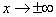
Прямая является наклонной асимптотой для графика при .

Ответ:

Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции. Корректный чертёж в конце урока.

Найти асимптоты графика функции

Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.

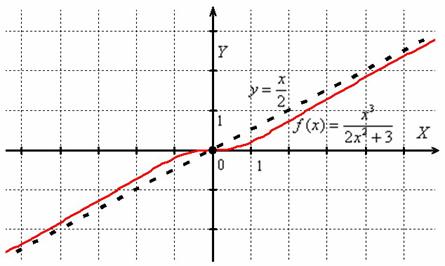
Очевидно, что обладателями «настоящих» наклонных асимптот являются графики тех дробно-рациональных функций, у которых старшая степень числителя на единицу больше старшей степени знаменателя. Если больше – наклонной асимптоты уже не будет (например, ).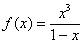

Но в жизни происходят и другие чудеса:

Исследовать график функции на наличие асимптот

Решение: функция непрерывна на всей числовой прямой, значит, вертикальные асимптоты отсутствует. Но вот наклонные вполне могут быть. Проверяем:

Вспоминаю, как ещё в ВУЗе столкнулся с похожей функцией и просто не мог поверить, что у неё есть наклонная асимптота. До тех пор, пока не вычислил второй предел:

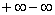
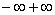
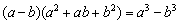
Строго говоря, здесь две неопределённости: и , но так или иначе, нужно использовать метод решения, который разобран в Примерах 5-6 статьи о пределах повышенной сложности. Умножаем и делим на сопряженное выражение, чтобы воспользоваться формулой :

Ответ:

Пожалуй, самая популярная наклонная асимптота.

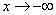
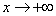
До сих пор бесконечности удавалось «стричь под одну гребёнку», но бывает, что у графика функции две разные наклонные асимптоты при и при :

Исследовать график функции на наличие асимптот

Решение: подкоренное выражение положительно, значит, область определения – любое действительно число, и вертикальных палок быть не может.

Проверим, существуют ли наклонные асимптоты.

Если «икс» стремится к «минус бесконечности», то: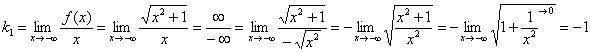
(при внесении «икса» под квадратный корень необходимо добавить знак «минус», чтобы не потерять отрицательность знаменателя)

Выглядит необычно, но здесь неопределённость «бесконечность минус бесконечность». Умножаем числитель и знаменатель на сопряженное выражение:

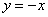
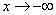
Таким образом, прямая является наклонной асимптотой графика при .

С «плюс бесконечностью» всё тривиальнее:

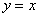
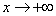
А прямая – при .

Ответ:

, если ;
, если .

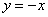
Не удержусь от графического изображения:

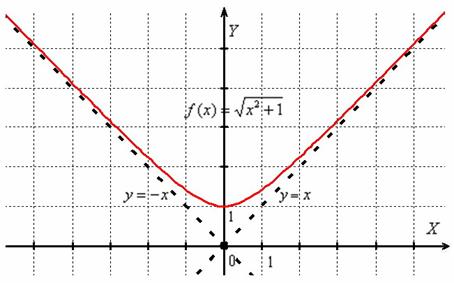
Это одна из ветвей гиперболы .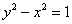

Не редкость, когда потенциальное наличие асимптот изначально ограничено областью определения функции:

Исследовать график функции на наличие асимптот

Решение: очевидно, что 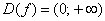, поэтому рассматриваем только правую полуплоскость, где есть график функции.

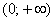
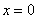
1) Функция непрерывна на интервале , а значит, если вертикальная асимптота и существует, то это может быть только ось ординат. Исследуем поведение функции вблизи точки справа:

Обратите внимание, здесь НЕТ неопределённости (на таких случаях акцентировалось внимание в начале статьи Методы решения пределов).

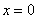
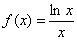
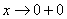
Таким образом, прямая (ось ординат) является вертикальной асимптотой для графика функции при .

2) Исследование на наклонную асимптоту можно провести по полной схеме, но в статье Правила Лопитал мы выяснили, что линейная функция более высокого порядка роста, чем логарифмическая, следовательно: 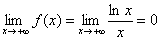(см. Пример 1 того же урока).

Вывод: ось абсцисс является горизонтальной асимптотой графика функции при .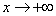

Ответ:

, если ;
, если .

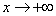
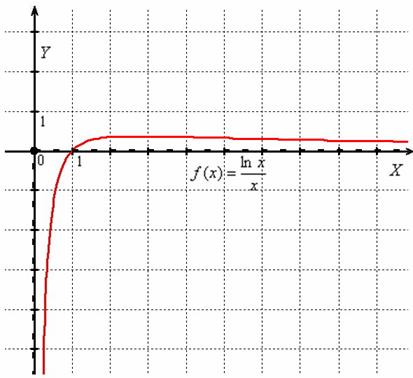
Чертёж для наглядности:

Интересно, что у вроде бы похожей функции 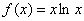асимптот нет вообще (желающие могут это проверить).

Два заключительных примера для самостоятельного изучения:

Исследовать график функции на наличие асимптот

Для проверки на вертикальные асимптоты сначала нужно найти область определения функции, а затем вычислить пару односторонних пределов в «подозрительных» точках. Наклонные асимптоты тоже не исключены, поскольку функция определена на «плюс» и «минус» бесконечности.

Исследовать график функции на наличие асимптот

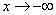
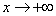
А здесь могут быть только наклонные асимптоты, причём направления , следует рассмотреть отдельно.

Надеюсь, вы отыскали нужную асимптоту =)

Решения и ответы:

Пример 2: Решение:
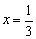
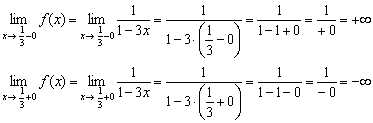
1) Вертикальные асимптоты. Функция терпит бесконечный разрыв в точке . Найдём односторонние пределы:

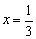
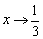
Прямая является вертикальной асимптотой графика функции при .
2) Наклонные асимптоты.

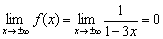
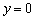
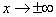
Прямая (ось абсцисс) является горизонтальной асимптотой графика функции при .
Ответ:

Чертёж к Примеру 3:

Пример 4: Решение:
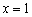
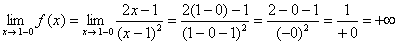
1) Вертикальные асимптоты. Функция терпит бесконечный разрыв в точке . Вычислим односторонние пределы:

Примечание: бесконечно малое отрицательное число в чётной степени равно бесконечно малому положительному числу: .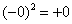

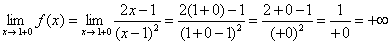
Прямая 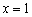является вертикальной асимптотой графика функции.
2) Наклонные асимптоты.

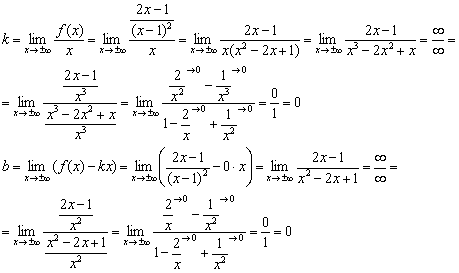
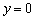
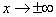
Прямая (ось абсцисс) является горизонтальной асимптотой графика функции при .
Ответ:

1) Исследуем функцию на наличие вертикальных асимптот. Найдём точки, в которых знаменатель обращается в ноль:

Действительных корней нет.

Исследуемая функция непрерывна на всей числовой прямой, значит, вертикальные асимптоты отсутствуют.

2) Наклонные асимптоты.

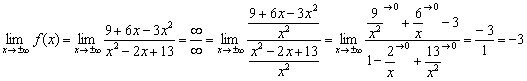
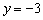
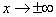
Прямая является горизонтальной асимптотой графика функции при .
Ответ:

Чертёж к Примеру 7:

Пример 8: Решение:
1) Вертикальные асимптоты. Исследуем точку .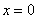
,
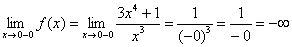
Примечание: бесконечно малое отрицательное число в нечётной степени равно бесконечно малому отрицательному числу: .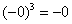
.
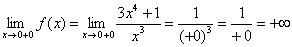
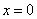
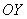
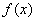
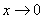
Прямая (ось ) является вертикальной асимптотой для графика , если .
2) Наклонные асимптоты:

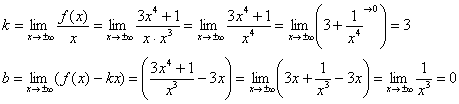
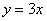
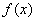
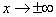
Прямая является наклонной асимптотой для графика при .
Ответ:

График данной функции:

Пример 12: Решение: найдём область определения функции:

.
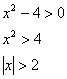
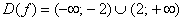
Помимо аналитического способа нахождения области определения можно использовать и метод интервалов.

1) Проверим наличие вертикальных асимптот. Для удобства и наглядности вычислений разложим аргумент логарифма на множители:

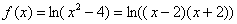
Вычислим односторонние пределы:

Таким образом, прямые являются вертикальными асимптотами для графика функции при и соответственно.

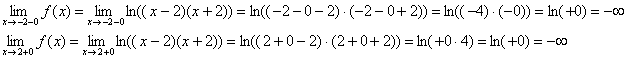
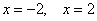
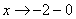
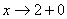
2) Наклонные асимптоты.

Дважды используем правило Лопиталя:
Первый предел конечен, находим второй предел:

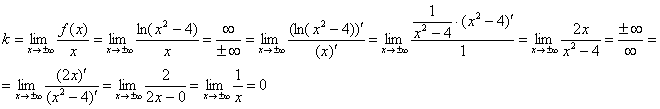
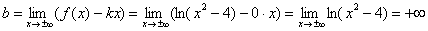
Значит, наклонные асимптоты отсутствуют.

, если ;
, если .

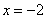
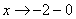
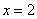
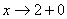
Пример 13: Решение: так как функция непрерывна на , то вертикальные асимптоты отсутствуют.

Выясним, есть ли у графика наклонные асимптоты:

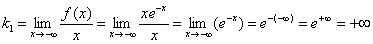
Значит, при у графика нет наклонной асимптоты.

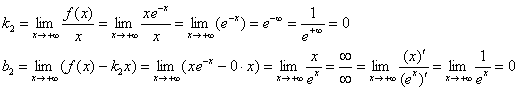
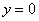
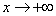
Таким образом, прямая является горизонтальной асимптотой графика данной функции при .
Ответ: ось абсцисс при .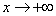

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Нули функции. Интервалы знакопостоянства функции.

Метод интервалов

Значительная доля материала, касающегося производных и исследования функций, традиционно относится к школьной программе, и данная статья не является исключением из правила. Сегодня мы потренируемся в нахождении нулей и интервалов знакопостоянства функции, а также подробно разберём метод интервалов, который можно сравнить с надёжной арматурой в стенах рассматриваемой темы.

Если же проект вашего здания находится на стадии котлована, пожалуйста, начните с вводного урока о графиках функций. Кроме того, желательно ознакомиться со статьями Область определения функции, Асимптоты графика, и, по существу, информация этой странички – логическое продолжение. Материал, естественно, будет полезен и старшеклассникам.

Источник