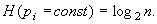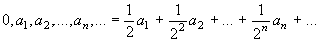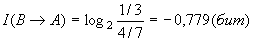Что такое вероятный подход

Что такое вероятный подход

Данный урок хочу посвятить теме «Измерение информации».

Выделяют следующие подходы к определению количества информации :

Данные подходы изучаются в школьном курсе информатики.

Вероятностный подход

Вероятностный подход связан с таким понятием как ВЕРОЯТНОСТЬ.
ВЕРОЯТНОСТЬ — это отношение количества тех наблюдений, при которых рассматриваемое событие наступило, к общему количеству наблюдений. Такая трактовка допустима в случае достаточно большого количества наблюдений или опытов.

Единицы измерения информации: бит, байт, кбайт и т.д.

За 1 бит информации принимают такое количество информации, которое находится в сообщении о том, что произошло одно событие из двух равновероятных.

1 бит — это количество информации, уменьшающее неопределенность знаний в два раза.

При РАВНОВЕРОЯТНОСТНОМ ПОДХОДЕ вероятности наступления того или иного события равны.

Для измерения количества информации, полученной нами при равновероятном событии, используем формулу

(где N — количество возможных исходов события (2 стороны в примере с монеткой),
i — количество информации, которое мы получим, при том или ином исходе события)

Другие задачи с разбором и для самостоятельного решения на тему «Вероятностный подход к измерению информации» смотрите в следующих выпусках.

При НЕРАВНОВЕРОЯТНОСТНОМ ПОДХОДЕ вероятности исходов событий не равны.

Пример: В коробке 16 карандашей. Из них 8 синих, 4 красных, 4 зеленых. Вероятность достать из коробки синий карандаш больше, чем вероятность достать зеленый или красный.

Для измерения количества информации при неравновероятностном подходе используют следующие формулы:

(где К — количество интересующих нас событий (достать синий карандаш K=8), N — общее количество события)

(где i — количество информации, которое мы получим, при том или ином исходе события)

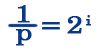
Вторая формула называется формулой Шеннона (правда в другом виде). В оригинале формула Шеннона выглядит так

Использование или неиспользовании этой формулы зависит от того, знают ли ученики про логарифм или нет.

Задача: В коробке 16 карандашей. Из них 8 синих, 4 красных, 4 зеленых. Сколько бит информации мы получим, вытащив из коробки синий карандаш?

Ответ : 1 бит информации мы получим, вытащив синий карандаш из коробки.

Продолжение рассмотрения этой темы смотрите в следующих постах.

Источник

Что такое вероятный подход

Вяткин В.Б.

ЗАДАЧА ОЦЕНКИ НЕГЭНТРОПИИ ОТРАЖЕНИЯ СИСТЕМНЫХ ОБЪЕКТОВ
И ТРАДИЦИОННЫЕ ПОДХОДЫ К КОЛИЧЕСТВЕННОМУ
ОПРЕДЕЛЕНИЮ ИНФОРМАЦИИ

Вероятностный подход к количественному
определению информации

Основополагающая роль в вероятностном подходе принадлежит энтропии множества вероятностей, формула которой была получена в 1948 году американским исследователем К. Шенноном. Предлагая для измерения количества информации свою знаменитую энтропийную меру, К. Шеннон руководствовался следующими соображениями.

Для такой меры Н выдвигается требование: она должна обладать следующими тремя свойствами.

1. Н должна быть непрерывной относительно .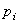

2. Если все 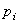равны, то Н должна быть монотонно возрастающей функцией от n.

3. Если выбор распадается на два последовательных выбора, то первоначальная Н должна быть взвешенной суммой индивидуальных значений Н каждого из выборов.

Последнее свойство поясняется рисунком 3, где показаны две ситуации выбора из трех возможностей, имеющих вероятности 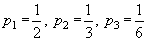. В левой ситуации выбор любой возможности является однократным, а в правой ситуации в двух случаях из трех необходимо предварительно сделать соответствующий дополнительный выбор из двух равновероятных возможностей.

Рис. 3. Выбор из трех возможностей

Согласно третьему свойству в левой и правой ситуациях значения Н должны быть одинаковы, что выражается следующим образом:

,

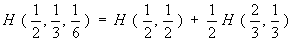
где коэффициент 1/2 является весовым множителем, указывающим, что второй выбор выполняется только в половине случаев.

Нетрудно видеть, что в том случае, когда все вероятности равны между собой, информационная мера Шеннона сводится к двоичному логарифму Хартли от числа возможностей:

Последнее свидетельствует о том, что во взаимоотношениях вероятностного и комбинаторного подходов соблюдается принцип соответствия, согласно которому «новая теория, претендующая на более широкую область применимости, чем старая, должна включать последнюю как предельный случай» [1 8, с. 1257].

Первое. Формула Шеннона может быть представлена как математическое ожидание величины :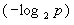

,

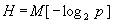
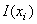
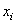
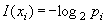
откуда частная информация , получаемая от отдельного события, состоящего в том, что некоторая система Х находится в состоянии _i имеет вид:

. (17)

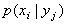
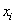
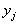
где — условная вероятность при наступлении .

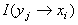
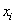
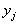
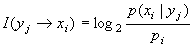
Из анализа структуры выражения ( 18) выводится частная информация о событии , содержащаяся в событии :

. (19)

Нетрудно видеть, что информация от события к событию может иметь как положительные, так и отрицательные значения, то есть:

и .

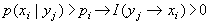
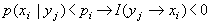
Н. Винер исходил из того, что в кибернетических системах элементарной формой информации является запись (запоминание) выбора одной из двух равновероятных возможностей, который он называл решением. Если известно, что значение некоторой непрерывной величины находится внутри интервала ( 0, 1 ) и стоит задача совершенно точно определить это значение, то количество выборов, которое необходимо при этом сделать, выражается бесконечной двоичной дробью:

где 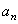имеет значение 0 или 1.

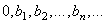
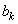
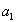
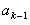
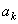
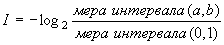
В действительности никакое измерение непрерывной величины не может быть совершенно точным, в связи с чем далее Н. Винер рассуждал следующим образом: «Если измерение имеет равномерно распределенную ошибку, лежащую в интервале длины , где есть первый разряд, не равный 0, то, очевидно, все решения от до и, возможно, до будут значащими, а все последующие нет. Число принятых решений, очевидно, близко

. (20)

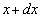
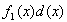
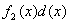
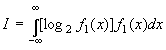
В том случае, когда априорно известно, что вероятность нахождения определяемой величины между x и равна , а апостериорная вероятность равна , Н. Винером предложено для оценки информации, которую дает апостериорная вероятность, использовать формулу:

. (21)

Нетрудно видеть, что при квантовании интервалов каким-либо образом формулы Винера (20) и (21) сводятся соответственно к двоичному логарифму Хартли и энтропии Шеннона. Причем в последнем случае тот факт, что в формуле Шеннона имеется отрицательный множитель ( –1 ), а в формуле Винера его нет, принципиального значения не имеет. Это наглядно показал Р.Эшби на примере двух способов измерения расстояний с помощью линейки [ 2 6]. Приведем этот пример.

Рис. 4. Измерение расстояния между точками P и Q
с помощью двух линеек W и S.

По способу Винера линейка W прикладывается к точкам P и Q произвольным образом, а расстояние PQ определяется как разность отсчетов: (отсчет для Q ) минус (отсчет для Р ). По способу Шеннона линейка S прикладывается строго определенным образом, а именно – нуль совмещается с точкой Q и тогда расстояние PQ определяется как: минус (отсчет для Р ). То есть принципиального различия в измерении количества информации по способам Винера и Шеннона не существует.

В заключение общей характеристики вероятностного подхода отметим, что его развитие отодвинуло в тень чисто комбинаторный подход определения количества информации, за внешней простотой которого, в соответствии с мнением А.Н. Колмогорова [ 12 ], потенциально скрываются нетривиальные решения различных информационных проблем.

Анализ приведенных сведений о вероятностном подходе к количественному определению информации позволяет высказать следующее.

,

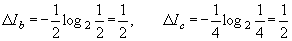
Формула частной информации, выражаемая логарифмом вероятности (17), в данном случае дает нам, что

,

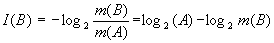
то есть мы опять получаем выше рассмотренное приложение формулы Бриллюэна (14).

В приведенном примере негэнтропия отражения представляет собой информацию, которую отражает группа шаров одного цвета ( белого или черного) относительно всей совокупности шаров, находящихся в урне, то есть она никакого отношения к информации «от события к событию» не имеет.

Примечания

Источник

Вероятностный подход к оценке количества информации. Формула Шеннона

Вы будете перенаправлены на Автор24

В основе нашего мира лежат три составляющие: вещество, энергия и информация. Как много в мире вещества, энергии и информации? Можно ли их измерить и как именно? Нам известны способы измерения количества вещества и энергии. Но как быть с информацией? Можно ли ее измерить?

Ранее уже отмечалось, что существует несколько подходов к оценке количества информации. Сейчас мы более подробно остановимся на одном из них.

Любое сообщение будет являться информативным, если оно пополняет знания человека, т.е. уменьшает неопределенность его знаний.

Равновероятные события

Например, при подбрасывании монеты мы пытаемся угадать, какой стороной она упадет. Возможен один из вариантов исхода: монета окажется в положении «орел» или «решка». Каждое из этих двух событий окажется равновероятным, т. е. ни одно из них не имеет преимущества перед другим. Перед подбрасыванием монеты никто не может знать, как она упадет, т.е. существует неопределенность знания. После же наступления события, наоборот, присутствует полная определенность, так как бросающий получает зрительное сообщение о положении монеты, которое, в свою очередь, уменьшает неопределенность его знания в два раза, поскольку из двух равновероятных событий произошло одно.

Другим примером является ситуация с шестигранным кубиком, т.е. перед броском никто не может знать, какой стороной он упадет. В данном случае присутствует возможность получить один результат из шести равновероятных. Таким образом, до броска неопределенность знаний бросающего будет равна 6, после же броска, она уменьшится ровно в 6 раз, поскольку именно 6 равновероятных событий может произойти.

Рассмотрим пример, где для экзамена приготовили 40 билетов. Вероятность событий, которые произойдут при вытягивании билета, будет равна 40. Причем эти события будут равновероятны. При этом неопределенность знаний студента перед выбором билета, будет равна 40. Соответственно неопределенность знания после того как студент взял билет уменьшится в 40 раз. Зададимся вопросом, зависит ли этот показатель от номера вытянутого билета. Нет, поскольку события равновероятны.

Готовые работы на аналогичную тему

Проанализировав все рассмотренные выше примеры, можно прийти к выводу, что чем больше исходное число возможных равновероятных событий, тем в большее количество раз уменьшается неопределенность знаний, и тем большее количество информации будет содержаться в сообщении о результатах опыта.

Неравновероятные события

Помимо этого, вероятность появления отдельных букв будет зависеть от того, какие буквы используются перед ними. Так, в русском языке после гласной никогда не может стоять мягкий знак, а также в словах не используются четыре гласные подряд и т.д. Разговорные языки имеют, как правило, свои особенности и закономерности. Именно поэтому количество информации, содержащееся в сообщениях любого разговорного языка, неприемлемо оценивать с помощью формулы Хартли, которая используется в алфавитном подходе к оценке информации и характерна для примеров с равновероятными событиями (примеры с монетой и кубиком).

Как определить, какое количество информации содержит, например, текст романа «Война и мир», или фрески и полотна великих итальянских художников, или генетический код человека? Ответы на эти вопросы и подобные им науке пока не известны и, по всей вероятности, еще не скоро будут известны. Однако всех интересует, возможно ли объективно оценить количество информации? К задаче подобного рода можно отнести следующий пример.

Как выяснить, являются ли равновероятными сообщения «первой выйдет из здания женщина» и «первым выйдет из здания мужчина»? Однозначного ответа на этот вопрос нет. Все будет зависеть от того, о каком именно здании идет речь. Если это, например, здание гинекологической клиники, то вероятность выйти первой у женщины очень высока, если это военная казарма, то вероятность выйти первым для мужчины будет выше, чем для женщины, а вот если это здание кинотеатра, то вероятности выйти первыми для мужчины и женщины будут одинаковыми.

Оценка количества информации. Формула Шеннона

Для решения задач подобного рода используется общая оценка количества информации, предложенная американским учёным Клодом Шенноном в 1948г. Созданная им формула определения количества информации способна учитывать возможную неодинаковую вероятность сообщений, содержащихся в наборе. Шеннон при создании формулы использовал применяемую в математике и гидродинамике вероятностную меру неопределенности (называемую энтропией) для того, чтобы в полной мере оценить состояние изучаемой системы и получить максимально возможную информацию о протекающих в этой системе процессах. Эта оценка количества информации, по существу, является вероятностной мерой, и, как оценка неопределенности, она отражает способность какого-либо источника проявлять все новые и новые состояния и таким образом отдавать информацию.

Шеннон определил энтропию как среднюю логарифмическую функцию множества вероятностей возможных состояний системы (возможных исходов опыта). Для расчета энтропии Шеннон предложил следующее уравнение:

Тогда количество информации, полученное в результате опыта, будет не что иное, как разность между энтропией системы до ($H_0$) и после ($H_1$) опыта:

причем если неопределенность в результате опыта полностью исключается, то имеем:

Рассмотрим пример, подтверждающий использование данной теории Шеннона на практике.

Решение. События улова пескаря или окуня не являются равновероятными, поскольку окуней в озере обитает намного меньше, чем пескарей.

Общее количество пескарей и окуней, обитающих в озере:

Определим вероятность улова пескаря:

Определим вероятность улова окуня:

Количество информации, содержащейся в сообщении об улове пескаря:

$I_1 = log_2(\frac<1><0,75>) » 0,43$ бит,

Количество информации, содержащейся в сообщении об улове окуня:

Количество информации, содержащейся в сообщении об улове рыбы (карася или окуня) рассчитывается по формуле Шеннона:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата написания статьи: 12 04 2016

Источник

Вероятностный подход к определению количества информации «Формула Шеннона. Применение ЭТ Excel для решения задач на нахождение количества информации»

Материал разработан на 2 спаренных урока.

Цели уроков: Сформировать у учащихся понимание вероятности, равновероятных событий и событий с различными вероятностями. Научить находить количество информации, используя вероятностный подход. Создать в Excel информационную модель для автоматизации процесса вычислений в задачах на нахождение количества информации, используя формулу Шеннона.

Требования к знаниям и умениям:

Учащиеся должны знать:

Учащиеся должны уметь:

Оборудование: доска, компьютер, мультимедийный проектор, карточки с заданиями, карточки-памятки, справочный материал.

Урок 1. Вероятностный подход к определению количества информации. Формула Шеннона

Ход урока

I. Организационный момент.

II. Проверка домашнего задания.

III. Постановка цели урока.

Задача: Какое сообщение содержит большее количество информации?

Первые три варианта учащиеся решают без затруднения. События равновероятны, поэтому можно применить для решения формулу Хартли. Но третье задание вызывает затруднение. Делаются различные предположения. Роль учителя: подвести учащихся к осмыслению, что в четвертом варианте мы сталкиваемся с ситуацией, когда события неравновероятны. Не все ситуации имеют одинаковые вероятности реализации. Существует много таких ситуаций, у которых вероятности реализации различаются. Например, если бросают несимметричную монету или «правило бутерброда».

Сегодня на уроке мы должны ответить на вопрос: как вычислить количество информации в сообщении о неравновероятном событии.

IV. Объяснение нового материала.

Для вычисления количества информации в сообщении о неравновероятном событии используют следующую формулу: I=log₂(1/p)

где I – это количество информации, р – вероятность события.

Вероятность события выражается в долях единицы и вычисляется по формуле: р=K/N,

где К – величина, показывающая сколько раз произошло интересующее нас событие, N – общее число возможных исходов какого-то процесса.

Вернемся к нашей задаче.

Пусть К₁ – это количество пирожков с повидлом, К₁=24

К₂ – количество пирожков с капустой, К₂=8

N – общее количество пирожков, N = К₁ +К₂=24+8=32

Вычислим вероятность выбора пирожка с разной начинкой и количество информации, которое при этом было получено.

Вероятность выбора пирожка с повидлом: р₁=24/32=3/4=0,75.

Вероятность выбора пирожка с капустой: р₂=8/32=1/4=0,25.

Обращаем внимание учащихся на то, что в сумме все вероятности дают 1.

Вычислим количество информации, содержащееся в сообщении, что Маша выбрала пирожок с повидлом: I₁=log₂(1/p₁)= log₂(1/0,75)= log₂1,3=1,15470 бит.

Вычислим количество информации, содержащееся в сообщении, если был выбран пирожок с капустой: I₂=log₂(1/p₂)= log₂(1/0,25)= log₂4=2 бит.

Пояснение: если учащиеся не умеют вычислять значение логарифмической функции, то можно использовать при решении задач этого урока следующие приемы:

Приложение 1. «Количество информации в сообщении об одном из N равновероятных событий: I= log₂N». (Приложение вы можете получить у автора статьи.)

При сравнении результатов вычислений получается следующая ситуация: вероятность выбора пирожка с повидлом больше, чем с капустой, а информации при этом получилось меньше. Это не случайность, а закономерность.

Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.

Вернемся к нашей задаче с пирожками. Мы еще не ответили на вопрос: сколько получим информации при выборе пирожка любого вида?

Ответить на этот вопрос нам поможет формула вычисления количества информации для событий с различными вероятностями, которую предложил в 1948 г. американский инженер и математик К.Шеннон.

можно расписать формулу в таком виде:

Рассмотрим формулу на нашем примере:

Теперь мы с вами можем ответить на вопрос задачи, которая была поставлена в начале урока. Какое сообщение содержит большее количество информации?

Ответ: в 1 сообщении.

Обратите внимание на 3 и 4 задачу. Сравните количество информации.

Мы видим, что количество информации достигает максимального значения, если события равновероятны.

Интересно, что рассматриваемые нами формулы классической теории информации первоначально были разработаны для технических систем связи, призванных служить обмену информацией между людьми. Работа этих систем определяется законами физики т.е. законами материального мира. Задача оптимизации работы таких систем требовала, прежде всего, решить вопрос о количестве информации, передаваемой по каналам связи. Поэтому вполне естественно, что первые шаги в этом направлении сделали сотрудники Bell Telephon Companie – X. Найквист, Р. Хартли и К. Шеннон. Приведенные формулы послужили К. Шеннону основанием для исчисления пропускной способности каналов связи и энтропии источников сообщений, для улучшения методов кодирования и декодирования сообщений, для выбора помехоустойчивых кодов, а также для решения ряда других задач, связанных с оптимизацией работы технических систем связи. Совокупность этих представлений, названная К. Шенноном “математической теорией связи”, и явилась основой классической теории информации. (Дополнительный материал можно найти на сайте http://polbu.ru/korogodin_information или прочитав книгу В.И. Корогодин, В.Л. Корогодина. Информация как основа жизни. Формула Шеннона.)

Можно ли применить формулу К. Шеннона для равновероятных событий?

Мы видим, что формула Хартли является частным случаем формулы Шеннона.

V. Закрепление изучаемого материала.

Задача: В корзине лежат 32 клубка красной и черной шерсти. Среди них 4 клубка красной шерсти.

Сколько информации несет сообщение, что достали клубок красной шерсти? Сколько информации несет сообщение, что достали клубок шерсти любой окраски?

Дано: К_к=4;N=32

Найти: I_к, I

Решение:

VI. Подведение итогов урока.

Урок 2. Применение ЭТ Excel для решения задач на нахождение количества информации

Пояснение: При решении задач на нахождение количества информации учащиеся не вычисляли значение логарифма, т.к. не знакомы с логарифмической функцией. Урок строился таким образом: сначала решались однотипные задачи с составлением формул, затем разрабатывалась табличная модель в Excel, где учащиеся делали вычисления. В конце урока озвучивались ответы к задачам.

Ход урока

I. Постановка целей урока

На этом уроке мы будем решать задачи на нахождение количества информации в сообщении о неравновероятных событиях и автоматизируем процесс вычисления задач данного типа.

Для решения задач на нахождение вероятности и количества информации используем формулы, которые вывели на прошлом уроке:

р_i=K_i/N; I_i=log₂(1/p_i);

II. Решение задач.

Ученикам дается список задач, которые они должны решить.

Задачи решаются только с выводами формул, без вычислений.

В озере обитает 12500 окуней, 25000 пескарей, а карасей и щук по 6250. Какое количество информации несет сообщение о ловле рыбы каждого вида. Сколько информации мы получим, когда поймаем какую-нибудь рыбу?

Решение:

III. Объяснение нового материала.

Задается вопрос ученикам:

1. Какие трудности возникают при решении задач данного типа? (Отв.: Вычисление логарифмов).

2. Нельзя ли автоматизировать процесс решения данных задач? (Отв.: можно, т.к. алгоритм вычислений в этих задачах один и тот же).

3. Какие программы используются для автоматизации вычислительного процесса? (Отв.: ЭТ Excel).

Давайте попробуем сделать табличную модель для вычисления задач данного типа.

Нам необходимо решить вопрос, что мы будем вычислять в таблице. Если вы внимательно присмотритесь к задачам, то увидите, что в одних задачах надо вычислить только вероятность событий, в других количество информации о происходящих событиях или вообще количество информации о событии.

Мы сделаем универсальную таблицу, где достаточно занести данные задачи, а вычисление результатов будет происходить автоматически.

Структура таблицы обсуждается с учениками. Роль учителя обобщить ответы учащихся.

При составлении таблицы мы должны учитывать:

Прежде чем демонстрировать заполнение таблицы, учитель повторяет правила ввода формул, функций, операцию копирования (домашнее задание к этому уроку).

При заполнении таблицы показывает как вводить логарифмическую функцию. Для экономии времени учитель демонстрирует уже готовую таблицу, а ученикам раздает карточки-памятки по заполнению таблицы.

Рассмотрим заполнение таблицы на примере задачи №1.

Рис. 1. Режим отображения формул

Рис. 2. Отображение результатов вычислений

Результаты вычислений занести в тетрадь.

Если в решаемых задачах количество событий больше или меньше, то можно добавить или удалить строчки в таблице.

VI. Практическая работа.

1. Сделать табличную модель для вычисления количества информации.

2. Используя табличную модель, сделать вычисления к задаче №2 (рис.3), результат вычисления занести в тетрадь.

3. Используя таблицу-шаблон, решить задачи №3,4 (рис.4, рис.5), решение оформить в тетради.

4. Сохранить таблицы в своих папках под именем «инф_вероятность».

В классе 30 человек. За контрольную работу по информатике получено 15 пятерок, 6 четверок, 8 троек и 1 двойка. Какое количество информации несет сообщение о том, что Андреев получил пятерку?

В коробке лежат кубики: 10 красных, 8 зеленых, 5 желтых, 12 синих. Вычислите вероятность доставания кубика каждого цвета и количество информации, которое при этом будет получено.

В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика?

VII. Подведение итогов урока.

Учитель оценивает работу каждого ученика. Оценивается не только практическая работа на компьютере, но и оформление решения задачи в тетради.

VIII. Домашняя работа.

1. Параграф учебника «Формула Шеннона», компьютерный практикум после параграфа.

2. Доказать, что формула Хартли – частный случай формулы Шеннона.

Литература:

Источник