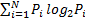Что такое вероятный подход измерения объема информации

Что такое вероятный подход измерения объема информации

Для информации существуют свои единицы измерения информации. Если рассматривать сообщения информации как последовательность знаков, то их можно представлять битами, а измерять в байтах, килобайтах, мегабайтах, гигабайтах, терабайтах и петабайтах.

Давайте разберемся с этим, ведь нам придется измерять объем памяти и быстродействие компьютера.

Единицей измерения количества информации является бит – это наименьшая (элементарная) единица.

Байт – основная единица измерения количества информации.

Байт – довольно мелкая единица измерения информации. Например, 1 символ – это 1 байт.

Производные единицы измерения количества информации

1 килобайт (Кб)=1024 байта =2 10 байтов

1 мегабайт (Мб)=1024 килобайта =2 10 килобайтов=2 20 байтов

1 гигабайт (Гб)=1024 мегабайта =2 10 мегабайтов=2 30 байтов

1 терабайт (Гб)=1024 гигабайта =2 10 гигабайтов=2 40 байтов

Методы измерения количества информации

Итак, количество информации в 1 бит вдвое уменьшает неопределенность знаний. Связь же между количеством возможных событий N и количеством информации I определяется формулой Хартли:

Алфавитный подход к измерению количества информации

При этом подходе отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка, т.е. его алфавит можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет в себе каждый символ:

Вероятностный подход к измерению количества информации

Этот подход применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:

I – количество информации,

N – количество возможных событий,

P_i – вероятность i-го события.

Задача 1.

Шар находится в одной из четырех коробок. Сколько бит информации несет сообщение о том, в какой именно коробке находится шар.

Имеется 4 равновероятных события (N=4).

По формуле Хартли имеем: 4=2 i . Так как 2 2 =2 i , то i=2. Значит, это сообщение содержит 2 бита информации.

Задача 2.

Чему равен информационный объем одного символа русского языка?

В русском языке 32 буквы (буква ё обычно не используется), то есть количество событий будет равно 32. Найдем информационный объем одного символа. I=log₂ N=log₂ 32=5 битов (2 5 =32).

Примечание. Если невозможно найти целую степень числа, то округление производится в большую сторону.

Задача 3.

Чему равен информационный объем одного символа английского языка?

Задача 4.

Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний (“включено” или “выключено”). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?

С помощью N лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2 N сигналов.

2 5 6 , поэтому пяти лампочек недостаточно, а шести хватит. Значит, нужно 6 лампочек.

Задача 5.

Метеостанция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.

В данном случае алфавитом является множество чисел от 0 до 100, всего 101 значение. Поэтому информационный объем результатов одного измерения I=log₂101. Но это значение не будет целочисленным, поэтому заменим число 101 ближайшей к нему степенью двойки, большей, чем 101. это число 128=2 7 . Принимаем для одного измерения I=log₂128=7 битов. Для 80 измерений общий информационный объем равен 80*7 = 560 битов = 70 байтов.

Задача 6.

Определите количество информации, которое будет получено после подбрасывания несимметричной 4-гранной пирамидки, если делают один бросок.

Пусть при бросании 4-гранной несимметричной пирамидки вероятности отдельных событий будут равны: p₁=1/2, p₂=1/4, p₃=1/8, p₄=1/8.

Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:

Задача 7.

Задача 8.

Оцените информационный объем следующего предложения:

Тяжело в ученье – легко в бою!

Так как каждый символ кодируется одним байтом, нам только нужно подсчитать количество символов, но при этом не забываем считать знаки препинания и пробелы. Всего получаем 30 символов. А это означает, что информационный объем данного сообщения составляет 30 байтов или 30 * 8 = 240 битов.

Источник

Что такое вероятный подход измерения объема информации

Данный урок хочу посвятить теме «Измерение информации».

Выделяют следующие подходы к определению количества информации :

Данные подходы изучаются в школьном курсе информатики.

Вероятностный подход

Вероятностный подход связан с таким понятием как ВЕРОЯТНОСТЬ.
ВЕРОЯТНОСТЬ — это отношение количества тех наблюдений, при которых рассматриваемое событие наступило, к общему количеству наблюдений. Такая трактовка допустима в случае достаточно большого количества наблюдений или опытов.

Единицы измерения информации: бит, байт, кбайт и т.д.

За 1 бит информации принимают такое количество информации, которое находится в сообщении о том, что произошло одно событие из двух равновероятных.

1 бит — это количество информации, уменьшающее неопределенность знаний в два раза.

При РАВНОВЕРОЯТНОСТНОМ ПОДХОДЕ вероятности наступления того или иного события равны.

Для измерения количества информации, полученной нами при равновероятном событии, используем формулу

(где N — количество возможных исходов события (2 стороны в примере с монеткой),
i — количество информации, которое мы получим, при том или ином исходе события)

Другие задачи с разбором и для самостоятельного решения на тему «Вероятностный подход к измерению информации» смотрите в следующих выпусках.

При НЕРАВНОВЕРОЯТНОСТНОМ ПОДХОДЕ вероятности исходов событий не равны.

Пример: В коробке 16 карандашей. Из них 8 синих, 4 красных, 4 зеленых. Вероятность достать из коробки синий карандаш больше, чем вероятность достать зеленый или красный.

Для измерения количества информации при неравновероятностном подходе используют следующие формулы:

(где К — количество интересующих нас событий (достать синий карандаш K=8), N — общее количество события)

(где i — количество информации, которое мы получим, при том или ином исходе события)

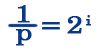
Вторая формула называется формулой Шеннона (правда в другом виде). В оригинале формула Шеннона выглядит так

Использование или неиспользовании этой формулы зависит от того, знают ли ученики про логарифм или нет.

Задача: В коробке 16 карандашей. Из них 8 синих, 4 красных, 4 зеленых. Сколько бит информации мы получим, вытащив из коробки синий карандаш?

Ответ : 1 бит информации мы получим, вытащив синий карандаш из коробки.

Продолжение рассмотрения этой темы смотрите в следующих постах.

Источник

Вероятностный подход измерения информации

Информация нуждается в измерении. На практике количество информации измеряется с точки зрения синтаксической адекватно­сти. Исторически сложились два подхода к измерению информации: вероятностный и объемный. В 1940-х гг. К. Шеннон предложил ве­роятностный подход, а работы по созданию ЭВМ способствовали развитию объемного подхода.

Рассмотрим вероятностный подход к измерению количества ин­формации.

Пусть системаа может принимать одно из N состояний в каждый момент времени, причем каждое из состояний равновероятно. На­пример, в качестве системы могут выступать опыты с подбрасывани­ем монеты (N = 2) или бросанием игральной кости (N= 6).Количество информации системы а вычисляется по формуле, предложенной Р. Хартли:H = H(a) = log₂N= lnN/ln2.При N =2 количество информации минимально и равно Н = 1. Поэтому в качестве единицы информации принимается количество информации, связанное с двумя равновероятными состояниями системы, например: «орел» — «решка», «ложь» — «истина». Такая еди­ница количества информации называется бит.Введем понятие вероятности. Вероятность событияА — это от­ношение числа случаев М, благоприятствующих событию А, к обще­му количеству случаев N:

Пример 1.Найти вероятность выпадения числа 6 при бросании кости.Решение. Всего граней у кости N = 6. Число 6 присутствует только на одной грани.

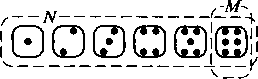Следовательно, вероятность выпадения числа 6 при бросании кости: Р=M/N/

Пример 2.Найти вероятность выпадения числа, большего 3, при бросании кости.

Решение. Всего граней у кости N = 6. Чисел, больших 3, на гранях кости М= 3.

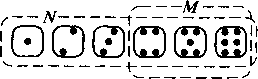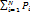
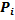
Следовательно, вероятность выпадения числа, большего 3, при бросании кости: P=M/N=3/6=1/2. Если N состояний системы не равновероятны, т.е. система на­ходится в i-м состоянии с вероятностью P_i и при этом все состояния системы образуют полную группу событий, т.е. сумма вероятностей равна: , то используются следующие формулы, предложенные Шенноном. Для определения количества информации:a)в одном (i-м) состоянии системы H=Log₂ (1/ );b)среднего количества информации во всех состояниях системы:

H=-

Из приведенных выражений следует, что количество информации максимально, если состояния системы равновероятны.

Объемный подход

Объем данных V в сообщении измеряется количеством символов (разрядов) в этом сообщении. В информатике в основном использу­ется двоичная система счисления, т.е. все числа представляются двумя цифрами: 0 и 1. Поэтому минимальной единицей измерения данных является бит. Таким образом, 1 бит — это либо 0, либо 1. Элемент, принимающий всего два значения, называется двухпози­ционным и просто реализуется аппаратно: например, двумя состоя­ниями «включено» —«выключено», «ток есть» —«ток отсутствует».

Более подробно о системах счисления будет рассказано позже.

Напомним таблицы размерностей:

1 байт = 8 бит (8 = 2 3 ); в международной системе кодов ASCII (AmtricanStandardCodeforInformationInterchange, Американский стандартный код обмена информацией) каждый символ кодировался одним байтом, чтопозволяло закодировать 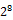= 256 символов, чего на первых порах хватало. Сейчас происходит переход к кодировке Unicode, где каждый символ кодируется двумя байтами, что позволяет кодировать 2 16 = 65536 символов, многократно увеличивая возможности кодирования.

1 Мбайт (мегабайт) = 1024 Кбайта (2 10 Кбайт или 2 20 байт).

1 Гбайт (гигабайт)=1024 Мбайта (2 10 Мбайт или 2 30 байт).

1 Тбайт (терабайт)=1024 Гбайта (2 10 Гбайт или 2 40 байт).

В недалеком будущем нас ожидают:

1 Пбайт (петабайт) =1024 Тбайта (2 10 Тбайт или 2 50 байт).

1 Эбайт (экзабайт) =1024 Пбайта (2 10 Пбайт или 2 60 байт).

1 Збайт (зеттабайт) =1024 Эбайта (2 10 Эбайт или 2 70 байт).

1 Йбайт (йоттабайт) =1024 Збайта (2 10 Збайт или 2 80 байт)

Пример 2.8.Сообщение в двоичной системе счисления 10010010 имеет объем данных V = 8 бит. Этот объем данных представляется 1 байтом.

Для удобства использования введены и более крупные единицы объема данных:

1 024 байт = 1 килобайт (Кбайт);

1 024 Кбайт = 1 мегабайт (Мбайт) = 1 024 2 байт = 1048 576 байт;

1 024 Мбайт = 1 гигабайт (Гбайт) = 1 024 3 байт;

1 024 Гбайт = 1 терабайт (Тбайт) = 1 024 4 байт;

1 024 Тбайт = 1 пентабайт (Пбайт) = 1 024 5 байт.

Общий объем информации в книгах, цифровых и аналоговых но­сителях за всю историю человечества составляет по оценкам 10 18 байт. Зато следующие 10 18 байт будут созданы в течение пяти —семи лет.

Отличие объема данных от количества информации заключается в следующем: объем данных выражается только целыми значениями, а количество информации — вещественными.

Формулу Хартли можно использовать для определения объема данных. При этом результат округляется в большую сторону, так как минимальной ячейкой памяти в ЭВМ является байт. Поэтому, заняв только часть байта (его несколько бит), оставшаяся часть байта не используется.

Пример 2.9.В сообщениях используются только первые шесть букв латинского алфавита: А, В,С, D, Е, F.Сколько байт необходи­мо для хранения сообщения «AABBCCD»?

Решение. Определим, сколько бит необходимо для хранения одной буквы по формуле Хартли:

Результат округлим в большую сторону, следовательно:

Тремя битами можно представить 8 комбинаций: ООО, 001, 010, 011, 100, 101, 110, 111. Для кодирования шести букв используются первые шесть комбинаций, а две последние комбинации не используются.

Для сообщения, состоящего из М = 7 букв, необходимо

V_c = М*Vb = 7 • 3 = 21 бит = 2,625 байт.

Результат вновь округлим в большую сторону:

Информатика и ее структура

Информатика — это наука и вид практической деятельности, связанные с процессами обработки информации с помощью вычис­лительной техники.

Термин «информатика» произошел от слияния двух французских слов information (информация) и automatique (автоматика) и до­словно определял новую науку об «автоматической обработке инфор­мации». В англоязычных странах информатика называется computerscience (наука о компьютерной технике).

Информатика представляет собой единство разнообразных от­раслей науки, техники и производства, связанных с переработкой информации с помощью вычислительной техники и телекоммуника­ционных средств связи в различных сферах человеческой деятель­ности.

Основная задача информатики заключается в определении общих закономерностей процессов обработки информации: создания, пере­дачи, хранения и использования в различных сферах человеческой деятельности. Прикладные задачи связаны с разработкой методов, необходимых для реализации информационных процессов с исполь­зованием технических средств.

Информатика включает в себя следующие разделы.

I. Теоретическая информатика.Это часть информатики, вклю­чающая в себя ряд подразделов, тесно связанных с другой наукой — математикой. В теории информации и кодирования изучается ин­формация как таковая, ее свойства, способы измерения количества информации. Областью исследования теории алгоритмов и автоматов являются методы переработки информации с помощью вычислитель­ных систем. Теория формальных языков и грамматик рассматривает правила построения простейших языков с небольшим числом син­таксических конструкций, называемых языками программирования. Теория принятия решений и исследования операций связана с ис­пользованием информации для принятия решений и оценки их опти­мальности. Теоретическая информатика использует математические методы для общего изучения процессов обработки информации.

II. Вычислительная техника.Это раздел, включающий в себя общие принципы построения вычислительных систем. Примером вычислительной системы является персональный компьютер, или ЭВМ. Этот раздел не связан с вопросами физической разработки, реализации и производства элементов вычислительных систем. Здесь рассматривается архитектура вычислительных систем— соглаше­ние о составе, назначении, функциональных возможностях и прин­ципах взаимодействия элементов внутри вычислительных систем и вычислительной системы с другими устройствами. Примерами прин­ципиальных, ставших классическими решений в этой области явля­ются архитектура фон Неймана компьютеров первых поколений, шинная архитектура ЭВМ, архитектура параллельной или многопро­цессорной обработки информации.

III. Программирование.Это деятельность, направленная на раз­работку программного обеспечения вычислительной техники. Про­граммирование делится на разделы, связанные с разработкой соот­ветствующих типов программного обеспечения. Программное обе­спечение, непосредственно управляющее составными частями вычислительной техники, называется системным. Системный уровень программного обеспечения составляют операционные системы. Слу­жебное программное обеспечение— это архиваторы, антивирусы, программы управления файлами и папками. Служебное программное обеспечение предназначено для выполнения некоторых вспомога­тельных функций. Прикладное программное обеспечение— это программы для решения большинства задач пользователя. Приклад­ное программное обеспечение включает в себя офисные, графиче­ские, справочные программы, среды разработки программ и др.

IV. Информационные системы.Это раздел информатики, свя­занный с решением проблем анализа потоков информации в раз­личных сложных системах, их оптимизации, структурировании, принципах хранения и поиска информации по запросу пользователя. Примерами информационных систем являются информационно­справочные, информационно-поисковые, глобальные системы или сети хранения и поиска информации.

V. Искусственный интеллект.Это область информатики, в ко­торой решаются сложнейшие проблемы, находящиеся на пересечении с психологией, физиологией, языкознанием и другими науками. Исторически сложились три основных направления развития систем искусственного интеллекта. Целью работ первого направления явля­ется создание алгоритмического и программного обеспечения вы­числительных машин, позволяющего решать интеллектуальные за­дачи не хуже человека. В рамках второго подхода объектом исследо­ваний являются структура и механизмы работы мозга человека, а конечная цель заключается в моделировании функционирования.

Источник

Вероятностный подход к определению количества информации «Формула Шеннона. Применение ЭТ Excel для решения задач на нахождение количества информации»

Материал разработан на 2 спаренных урока.

Цели уроков: Сформировать у учащихся понимание вероятности, равновероятных событий и событий с различными вероятностями. Научить находить количество информации, используя вероятностный подход. Создать в Excel информационную модель для автоматизации процесса вычислений в задачах на нахождение количества информации, используя формулу Шеннона.

Требования к знаниям и умениям:

Учащиеся должны знать:

Учащиеся должны уметь:

Оборудование: доска, компьютер, мультимедийный проектор, карточки с заданиями, карточки-памятки, справочный материал.

Урок 1. Вероятностный подход к определению количества информации. Формула Шеннона

Ход урока

I. Организационный момент.

II. Проверка домашнего задания.

III. Постановка цели урока.

Задача: Какое сообщение содержит большее количество информации?

Первые три варианта учащиеся решают без затруднения. События равновероятны, поэтому можно применить для решения формулу Хартли. Но третье задание вызывает затруднение. Делаются различные предположения. Роль учителя: подвести учащихся к осмыслению, что в четвертом варианте мы сталкиваемся с ситуацией, когда события неравновероятны. Не все ситуации имеют одинаковые вероятности реализации. Существует много таких ситуаций, у которых вероятности реализации различаются. Например, если бросают несимметричную монету или «правило бутерброда».

Сегодня на уроке мы должны ответить на вопрос: как вычислить количество информации в сообщении о неравновероятном событии.

IV. Объяснение нового материала.

Для вычисления количества информации в сообщении о неравновероятном событии используют следующую формулу: I=log₂(1/p)

где I – это количество информации, р – вероятность события.

Вероятность события выражается в долях единицы и вычисляется по формуле: р=K/N,

где К – величина, показывающая сколько раз произошло интересующее нас событие, N – общее число возможных исходов какого-то процесса.

Вернемся к нашей задаче.

Пусть К₁ – это количество пирожков с повидлом, К₁=24

К₂ – количество пирожков с капустой, К₂=8

N – общее количество пирожков, N = К₁ +К₂=24+8=32

Вычислим вероятность выбора пирожка с разной начинкой и количество информации, которое при этом было получено.

Вероятность выбора пирожка с повидлом: р₁=24/32=3/4=0,75.

Вероятность выбора пирожка с капустой: р₂=8/32=1/4=0,25.

Обращаем внимание учащихся на то, что в сумме все вероятности дают 1.

Вычислим количество информации, содержащееся в сообщении, что Маша выбрала пирожок с повидлом: I₁=log₂(1/p₁)= log₂(1/0,75)= log₂1,3=1,15470 бит.

Вычислим количество информации, содержащееся в сообщении, если был выбран пирожок с капустой: I₂=log₂(1/p₂)= log₂(1/0,25)= log₂4=2 бит.

Пояснение: если учащиеся не умеют вычислять значение логарифмической функции, то можно использовать при решении задач этого урока следующие приемы:

Приложение 1. «Количество информации в сообщении об одном из N равновероятных событий: I= log₂N». (Приложение вы можете получить у автора статьи.)

При сравнении результатов вычислений получается следующая ситуация: вероятность выбора пирожка с повидлом больше, чем с капустой, а информации при этом получилось меньше. Это не случайность, а закономерность.

Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.

Вернемся к нашей задаче с пирожками. Мы еще не ответили на вопрос: сколько получим информации при выборе пирожка любого вида?

Ответить на этот вопрос нам поможет формула вычисления количества информации для событий с различными вероятностями, которую предложил в 1948 г. американский инженер и математик К.Шеннон.

можно расписать формулу в таком виде:

Рассмотрим формулу на нашем примере:

Теперь мы с вами можем ответить на вопрос задачи, которая была поставлена в начале урока. Какое сообщение содержит большее количество информации?

Ответ: в 1 сообщении.

Обратите внимание на 3 и 4 задачу. Сравните количество информации.

Мы видим, что количество информации достигает максимального значения, если события равновероятны.

Интересно, что рассматриваемые нами формулы классической теории информации первоначально были разработаны для технических систем связи, призванных служить обмену информацией между людьми. Работа этих систем определяется законами физики т.е. законами материального мира. Задача оптимизации работы таких систем требовала, прежде всего, решить вопрос о количестве информации, передаваемой по каналам связи. Поэтому вполне естественно, что первые шаги в этом направлении сделали сотрудники Bell Telephon Companie – X. Найквист, Р. Хартли и К. Шеннон. Приведенные формулы послужили К. Шеннону основанием для исчисления пропускной способности каналов связи и энтропии источников сообщений, для улучшения методов кодирования и декодирования сообщений, для выбора помехоустойчивых кодов, а также для решения ряда других задач, связанных с оптимизацией работы технических систем связи. Совокупность этих представлений, названная К. Шенноном “математической теорией связи”, и явилась основой классической теории информации. (Дополнительный материал можно найти на сайте http://polbu.ru/korogodin_information или прочитав книгу В.И. Корогодин, В.Л. Корогодина. Информация как основа жизни. Формула Шеннона.)

Можно ли применить формулу К. Шеннона для равновероятных событий?

Мы видим, что формула Хартли является частным случаем формулы Шеннона.

V. Закрепление изучаемого материала.

Задача: В корзине лежат 32 клубка красной и черной шерсти. Среди них 4 клубка красной шерсти.

Сколько информации несет сообщение, что достали клубок красной шерсти? Сколько информации несет сообщение, что достали клубок шерсти любой окраски?

Дано: К_к=4;N=32

Найти: I_к, I

Решение:

VI. Подведение итогов урока.

Урок 2. Применение ЭТ Excel для решения задач на нахождение количества информации

Пояснение: При решении задач на нахождение количества информации учащиеся не вычисляли значение логарифма, т.к. не знакомы с логарифмической функцией. Урок строился таким образом: сначала решались однотипные задачи с составлением формул, затем разрабатывалась табличная модель в Excel, где учащиеся делали вычисления. В конце урока озвучивались ответы к задачам.

Ход урока

I. Постановка целей урока

На этом уроке мы будем решать задачи на нахождение количества информации в сообщении о неравновероятных событиях и автоматизируем процесс вычисления задач данного типа.

Для решения задач на нахождение вероятности и количества информации используем формулы, которые вывели на прошлом уроке:

р_i=K_i/N; I_i=log₂(1/p_i);

II. Решение задач.

Ученикам дается список задач, которые они должны решить.

Задачи решаются только с выводами формул, без вычислений.

В озере обитает 12500 окуней, 25000 пескарей, а карасей и щук по 6250. Какое количество информации несет сообщение о ловле рыбы каждого вида. Сколько информации мы получим, когда поймаем какую-нибудь рыбу?

Решение:

III. Объяснение нового материала.

Задается вопрос ученикам:

1. Какие трудности возникают при решении задач данного типа? (Отв.: Вычисление логарифмов).

2. Нельзя ли автоматизировать процесс решения данных задач? (Отв.: можно, т.к. алгоритм вычислений в этих задачах один и тот же).

3. Какие программы используются для автоматизации вычислительного процесса? (Отв.: ЭТ Excel).

Давайте попробуем сделать табличную модель для вычисления задач данного типа.

Нам необходимо решить вопрос, что мы будем вычислять в таблице. Если вы внимательно присмотритесь к задачам, то увидите, что в одних задачах надо вычислить только вероятность событий, в других количество информации о происходящих событиях или вообще количество информации о событии.

Мы сделаем универсальную таблицу, где достаточно занести данные задачи, а вычисление результатов будет происходить автоматически.

Структура таблицы обсуждается с учениками. Роль учителя обобщить ответы учащихся.

При составлении таблицы мы должны учитывать:

Прежде чем демонстрировать заполнение таблицы, учитель повторяет правила ввода формул, функций, операцию копирования (домашнее задание к этому уроку).

При заполнении таблицы показывает как вводить логарифмическую функцию. Для экономии времени учитель демонстрирует уже готовую таблицу, а ученикам раздает карточки-памятки по заполнению таблицы.

Рассмотрим заполнение таблицы на примере задачи №1.

Рис. 1. Режим отображения формул

Рис. 2. Отображение результатов вычислений

Результаты вычислений занести в тетрадь.

Если в решаемых задачах количество событий больше или меньше, то можно добавить или удалить строчки в таблице.

VI. Практическая работа.

1. Сделать табличную модель для вычисления количества информации.

2. Используя табличную модель, сделать вычисления к задаче №2 (рис.3), результат вычисления занести в тетрадь.

3. Используя таблицу-шаблон, решить задачи №3,4 (рис.4, рис.5), решение оформить в тетради.

4. Сохранить таблицы в своих папках под именем «инф_вероятность».

В классе 30 человек. За контрольную работу по информатике получено 15 пятерок, 6 четверок, 8 троек и 1 двойка. Какое количество информации несет сообщение о том, что Андреев получил пятерку?

В коробке лежат кубики: 10 красных, 8 зеленых, 5 желтых, 12 синих. Вычислите вероятность доставания кубика каждого цвета и количество информации, которое при этом будет получено.

В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика?

VII. Подведение итогов урока.

Учитель оценивает работу каждого ученика. Оценивается не только практическая работа на компьютере, но и оформление решения задачи в тетради.

VIII. Домашняя работа.

1. Параграф учебника «Формула Шеннона», компьютерный практикум после параграфа.

2. Доказать, что формула Хартли – частный случай формулы Шеннона.

Литература:

Источник