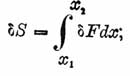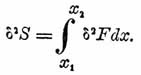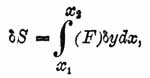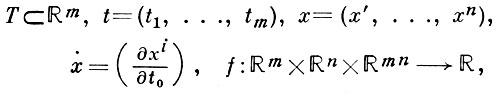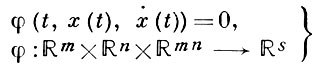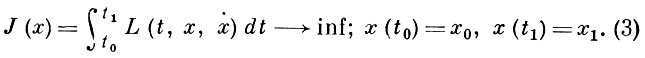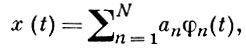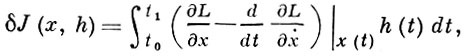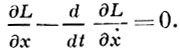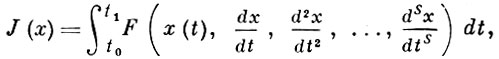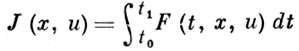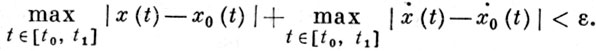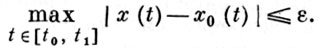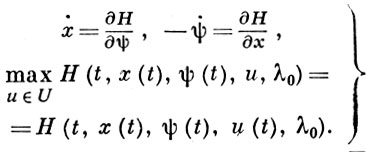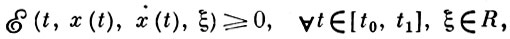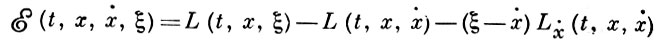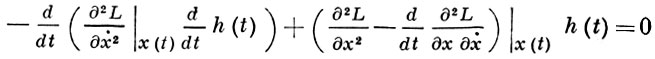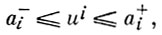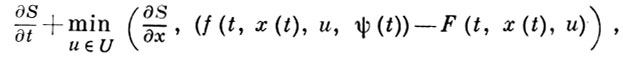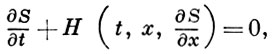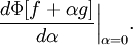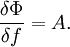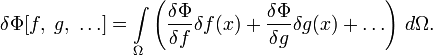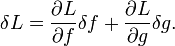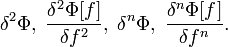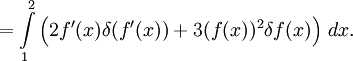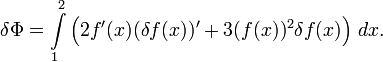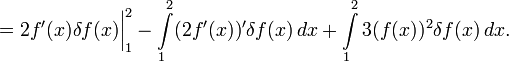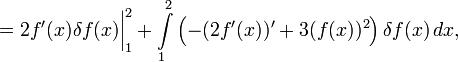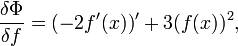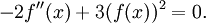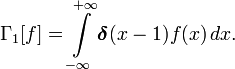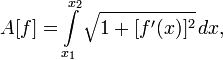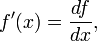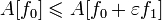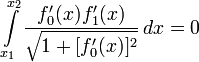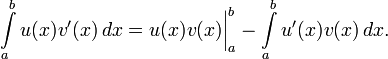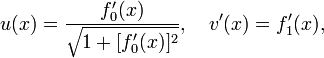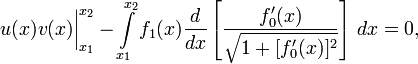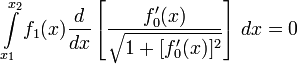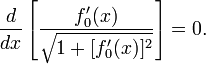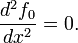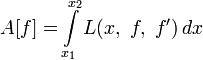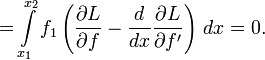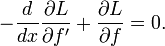Что такое вариационное исчисление

Вариационное исчисление

Полезное

Смотреть что такое «Вариационное исчисление» в других словарях:

ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ — раздел математики, посвященный нахождению наибольших и наименьших значений переменных величин, зависящих от выбора одной или нескольких функций (такие величины называются функционалами). К числу задач вариационного исчисления относятся, напр.,… … Большой Энциклопедический словарь

ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ — математическая наука, имеющая целью исследование изменений, происходящих в функции, если переменные, входящие в состав её, получат некоторое приращение. Открыто Лагранжем в 1760. Словарь иностранных слов, вошедших в состав русского языка.… … Словарь иностранных слов русского языка

вариационное исчисление — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN calculus of variations … Справочник технического переводчика

Вариационное исчисление — Вариационное исчисление это раздел функционального анализа, в котором изучаются вариации функционалов. Самая типичная задача вариационного исчисления состоит в том, чтобы найти функцию, на которой заданный функционал достигает… … Википедия

Вариационное исчисление — математическая дисциплина, посвященная отысканию экстремальных (наибольших и наименьших) значений функционалов переменных величин, зависящих от выбора одной или нескольких функций. В. и. является естественным развитием той главы… … Большая советская энциклопедия

ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ — раздел математики, занимающийся решением задач, связанных с отысканием экстремальных значений; одной из таких задач является нахождение кривой, обращающей некоторую величину в минимум (или в максимум). И.Ньютон решил задачу такого типа, найдя… … Энциклопедия Кольера

ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ — численные методы раздел вычислительной математики, посвященный методам отыскания экстремальных значений функционалов. Численные методы В. и. принято разделять на два больших класса: непрямые и прямые методы. Непрямые методы основаны на… … Математическая энциклопедия

вариационное исчисление — раздел математики, посвящённый нахождению наибольших и наименьших значений переменных величин, зависящих от выбора одной или нескольких функций (такие величины называются функционалами). К числу задач вариационного исчисления относятся, например … Энциклопедический словарь

ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ — (от лат. variatio изменение) раздел математики, посвящённый нахождению наибольших и наименьших значений функционале в перем. величин, зависящих от выбора одной или неск. ф ций. В. и. широко используется для решения ряда задач физики, техники,… … Большой энциклопедический политехнический словарь

Источник

ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ

Весьма широкий круг задач классич. В. и. описывает следующая схема. Требуется минимизировать функционал

при ограничениях типа равенств:

и некоторых краевых условиях: x|_∂T ∈ Г. Задачи такого типа наз. Лагранжа задачами. Кроме задач Лагранжа, рассматривают еще Майера задачи, Больца задачи и ряд других.

Наиболее элементарной среди задач классич. В. и. является простейшая задача В. и., когда в (1) t и x одномерны, ограничения (2) отсутствуют, а граничные условия закрепленные:

К этому типу относится задача о брахистохроне или о кривой наикратчайшего спуска. С задачей о брахистохроне обычно связывают начало истории классич. В. и.

Теоретич. основы классич. В. и. были заложены Л. Эйлером (L. Euler) и Ж. Лагранжем (J. Lagrange) в 18 в: Ими же были вскрыты важнейшие связи этой дисциплины с механикой и физикой. На первом же этапе развития В. и. усилиями в основном Г. Лейбница (G. Leibniz), Я. и И. Бернулли (Jacob et Johann Bernoulli), Л. Эйлера и Ж. Лагранжа получили решение многие конкретные задачи (о геодезических, о поверхности вращения, ряд изопериметрич. задач и т. п.).

В В. и. изучаются алгоритмич. методы отыскания экстремумов, методы получения необходимых и достаточных условий, условия, гарантирующие существование экстремума, качественные вопросы и т. п. Среди алгоритмич. методов нахождения экстремумов важнейшее место занимают прямые методы.

Прямые методы. Л. Эйлер (1768) создал метод приближенного (численного) решения задач В. и., к-рый получил назв. метода ломаных Эйлера. С этого момента начались исследования путей численного решения экстремальных задач. Метод Эйлера был первым представителем большого класса методов, наз. прямыми методами В. и. Эти методы основаны на редукции задачи отыскания экстремума функционала к задаче математич. анализа об отыскании экстремума функции многих переменных.

В 20 в. интерес к прямым методам значительно возрос. Прежде всего были предложены новые способы редукции к задаче об экстремуме функции конечного числа переменных. Эти идеи могут быть пояснены на примере минимизации функционала (3) при условии

Пусть разыскивается решение задачи в форме

Для простейшей задачи В. и.:

Основные результаты, относящиеся к простейшей задаче В. и., переносятся на общий случай функционалов вида

Рассмотрим тот случай, когда в задаче (1), (2) t одномерно и система φ(t, х, ẋ) может быть частично разрешена относительно последних переменных. Тогда получается задача о минимизации функционала

при дифференциальной связи

и граничных условиях:

Примером граничных условий типа (7) могут служить закрепленные условия как в задаче (3). В задачах оптимального управления помимо условий (6) и (7) накладывают еще и «неклассические» условия, напр.

Иными словами, здесь фиксируется близость не только фазовых переменных, но и скоростей (управлений). Говорят, что функция доставляет сильный экстремум, если можно указать такое ε > 0, что J(X) ≥ J(х₀) для всех допустимых абсолютно непрерывных функций x(t) (для к-рых J(x) существует), удовлетворяющих условиям x(t₀) = x₀(t₀), x(t₁) = x₀(t₁) и

Здесь фиксируется лишь близость фазовых переменных.

Если x₀(t) реализует сильный экстремум, то эта функция реализует тем более и слабый экстремум, поэтому достаточные условия сильного экстремума являются достаточными условиями и слабого. С другой стороны, из отсутствия слабого экстремума следует отсутствие сильного экстремума, т. е. необходимые условия слабого экстремума являются необходимыми условиями сильного экстремума.

Если приложить принцип максимума Понтрягина к задаче (3), то получится, что для того чтобы кривая x(t) доставляла сильный минимум в задаче (3), необходимо, чтобы она была экстремалью (т. е. удовлетворяла уравнению Эйлера (4)) и, кроме того, чтобы выполнялось необходимое условие Вейерштрасса:

— так наз. -функция Вейерштрасса.

Помимо условий типа (4) и (10), носящих локальный характер (т. е. проверяемых в каждой точке экстремали), имеется необходимое условие глобального характера, связанное с поведением множества экстремалей, близких к заданной экстремали (см. Якоби условие). Для задачи (3) условие Якоби состоит в следующем. Для того чтобы экстремаль x(t) доставляла минимум в задаяе (3), необходимо, чтобы решение уравнения (Якоби уравнения)

с краевыми условиями h(t₀) = 0, ḣ(t₀)≠0 не имело бы нулей в интервале (t₀, t₁). Нули решения h(t) уравнения (11) наз. точками, сопряженными с точкой t₀. Таким образом, условие Якоби заключается в том, что интервал (t₀, t₁) не должен содержать точек, сопряженных с t₀.

Необходимые условия слабого минимума δJ = 0, δ 2 J ≥0 являются точными аналогами условий минимума f'(х) = 0, f»(х) ≥ 0 для функций одного переменного. Условие Якоби при выполнении Лежандра условия (усиленного) является необходимым условием неотрицательности второй вариации. Это приводит к следующему результату: для того чтобы функция x(t) реализовывала слабый минимум функционала (3), необходимо, чтобы: а) функция x(t) удовлетворяла уравнению Эйлера, б) выполнялось условие Лежандра 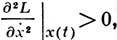, в) интервал (t₀, t₁) не содержал точек, сопряженных с точкой t₀ (при условии, что выполняется усиленное условие Лежандра).

Достаточные условия слабого минимума таковы: функция x(t) должна быть экстремалью, на ней выполняется усиленное условие Лежандра и полуинтервал (t₀, t₁] не содержит точек, сопряженных с точкой t₀. Для того чтобы кривая x(t) доставляла сильный минимум, достаточно, чтобы, помимо сформулированных достаточных условий слабого минимума, выполнялось Вейерштрасса условие достаточное.

Имеется большое число задач, к-рые сводятся к задаче Лагранжа, но при дополнительном ограничении типа (8). Такие задачи получили назв. задач оптимального управления. Для теории оптимального управления должен был быть разработан специальный аппарат. Им и явился принцип максимума Понтрягина.

наз. уравнением Беллмана (см. Динамическое программирование). Для задан классич. В. и. S-функция S(t, х) (или функция действия) должна удовлетворять уравнению Гамильтона-Якоби:

Связь В. и. с задачами теории уравнений с частными производными была обнаружена уже в 19 в. П. Дирихле (P. Dirichlet) показал, что решение краевых задач для уравнения Лапласа эквивалентно решению нек-рой вариационной задачи. Пусть, напр., имеется нек-рое линейное операторное уравнение

f(x₀ + λe) ≥ f(x₀) для любого λ ∈ [0, λ*_e]. Для того чтобы х₀ реализовал минимум функции f(x), необходимо, чтобы пересечение конусов Г_G(х₀) и Г_f(x₀) было пустым. Это условие столь же элементарно, как и условие обращения в нуль вариации, однако из него вытекают не только те результаты, к-рые можно получить классич. методами В. и.; оно позволяет подойти к проблемам гораздо более сложным, напр. к исследованию экстремальных значений недифференцируемых функционалов (см. [6]).

Лит.: [1] Смирнов В. И., Курс высшей математики, 5 изд., т. 4, М., 1958; [2] Лаврентьев М. А., Люстерник Л. А., Курс вариационного исчисления, 2 изд., М.-Л., 1950; [3] Блисс Г. А., Лекции по вариационному исчислению, пер. с англ., М., 1950; [4] Михлин С. Г., Вариационные методы в математической физике, М., 1957; [5] Понтрягин Л. С., (и др.), Математическая теория оптимальных процессов, 2 изд., М., 1969; [6] Пшеничный Б. Н., Необходимые условия экстремума, М., 1969; [7] Люстерник Л. А., Шнирельман Л. Г., Топологические методы в вариационных задачах, М., 1930.

Источник

Вариационное исчесление

Вариационное исчисление — это раздел математики, в котором изучаются вариации функционалов. Самая типичная задача вариационного исчисления состоит в том, чтобы найти функцию, на которой функционал достигает экстремального значения. Методы вариационного исчисления широко применяются в различных областях математики, в дифференциальной геометрии с их помощью ищут геодезические и минимальные поверхности. В физике вариационный метод — одно из мощнейших орудий получения уравнений движения (см. например Принцип наименьшего действия), как для дискретных, так и для распределённых систем, в том числе и для физических полей. Методы вариационного исчисления применимы и в статике (см. Вариационные принципы).

Важнейшими понятиями вариационного исчисления являются следующие:

Никак не связана с вариационным вычислением совпадающая по названию вариация функции в анализе.

Термин варьирование (варьировать) — применяется в вариационном исчислении для обозначения нахождения вариации или вариационной производной (это аналог термина дифференцирование для случая бесконечномерного аргумента, являющегося предметом вариационного исчисления). Также нередко для краткости (особенно в приложениях) термин варьирование применяется для обозначения решения вариационной задачи, сводимой к нахождению вариационной производной и приравнивания её нулю.

Вариационная задача означает, как правило, нахождение функции (в рамках вариационного исчисления — уравнения на функцию), удовлетворяющей условию стационарности некоторого заданного функционала, то есть такой функции, (бесконечно малые) возмущения которой не вызывают изменения функционала по крайней мере в первом порядке малости. Также вариационной задачей называют тесно связанную с этим задачу нахождения функции (уравнения на функцию), на которой данный функционал достигает локального экстремума (во многом эта задача сводится к первой, иногда практически полностью). Обычно при таком употреблении терминов подразумевается, что задача решается методами вариационного исчисления.

Типичными примерами вариационной задачи являются изопериметрические задачи в геометрии и механике; в физике — задача нахождения уравнений поля из заданного вида действия для этого поля.

Содержание

История

Одной из первых задач вариационного исчисления известных в истории была задача Дидоны. Другой исторической задачей вариационного исчисления, давшей толчок к развитию этого направления математики является задача о брахистохроне. Решающий вклад в развитие вариационного исчисления внесли Леонард Эйлер и Жозеф Лагранж, первому из которых принадлежит первое систематическое изложение вариационного исчисления и сам термин, второй же получил независимо многие основополагающие результаты и ввёл понятие вариации.

Неформальное обсуждение

Содержанием вариационного исчисления является обобщение понятия дифференциала и производной функции конечномерного векторного аргумента на случай функционала — функции, областью определения которой служит некое множество или пространство функций, а значения лежат в множестве вещественных чисел (иногда комплексных, что мало меняет что-то по существу).

Функционал Φ[f] ставит в соответствие каждой конкретной функции f из его области определения — определённое число.

Нетрудно написать для функционала аналоги дифференциала и производной по направлению.

Вариация

Аналогом дифференциала (первого дифференциала) является в вариационном исчислении вариация (первая вариация):

Как видим, δΦ сама в свою очередь является функционалом, так как она, вообще говоря, различна для разных f (также и при разных δf ).

Таким образом, это прямой аналог одномерного и конечномерного дифференциала:

— точно так же понимаемого как линейная часть приращения функции y при бесконечно малом приращении аргумента x (или линейный член при разложении y по степеням dx вблизи точки x ).

Производная по направлению

Производной функционала Φ в точке f по направлению g очевидно, будет

Вариационная производная

Для интегральных функционалов, которые являются очень важным для математики и приложений случаем, можно ввести не только аналог дифференциала и производную по направлению, но и производную Фреше — аналог конечномерного (градиента), называемую вариационной производной.

То есть, в полной аналогии с конечномерным случаем, когда

,

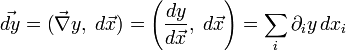
Для функционала имеем

,

Иными словами, если можно представить вариацию

Так же легко обобщается понятие вариационной производной на случай функционалов от нескольких аргументов [1] :

Выражая бесконечно малую разность функции нескольких аргументов как полный дифференциал, получим:

Вариации и вариационные производные второго и высших порядков

Для функционалов, зависящих от нескольких функций, можно также ввести понятие смешанных вариационных производных разного порядка, например:

Здесь мы не будем останавливаться на этом подробно, всё делается полностью аналогично введению соответствующих дифференциалов и производных для функции конечномерного аргумента.

Функционал вблизи конкретной точки в пространстве функций раскладывается в ряд Тейлора, если, конечно, вариационные производные всех порядков существуют. Как и в конечномерных случаях, сумма конечного числа членов этого ряда даёт значение функционала с определённой точностью (соответствующего порядка малости) лишь при небольших отклонениях его аргумента (при бесконечно малых). Кроме того, как и в случае функций конечномерного аргумента, ряд Тейлора (сумма всех членов) может не сходиться к функционалу, в него разложенному, при любых ненулевых конечных смещениях, хотя такие случаи достаточно редки в приложениях.

Применение вариационного исчисления

Хотя задачи, к которым применимо вариационное исчисление, заметно шире, в приложениях они главным образом сводятся к двум основным задачам:

Очевидно, обе задачи тесно связаны, и решение второй сводится (при должной гладкости функционала) к решению первой, а затем проверке, действительно ли достигается локальный экстремум (что делается независимо вручную, или — более систематически — исследованием вариационных производных второго и, если все они одного знака и хотя бы одна из них равна нулю, то производных более высокого порядка). В описанном процессе выясняется и тип экстремума. Нередко (например, когда функция стационарного функционала единственная, а все изменения функционала при любом большом возмущении имеют один и тот же знак) решение вопроса, экстремум ли это и какого он типа, заранее очевидно.

При этом очень часто задача (1) оказывается не менее или даже более важной, чем задача (2), даже когда классификация стационарной точки неопределённа (то есть она может оказаться минимумом, максимумом или седловой точкой, а также слабым экстремумом, точкой, вблизи которой функционал точно постоянен или отличается от постоянного в более высоком порядке, чем второй). Например, в механике (и вообще в физике) кривая или поверхность стационарной потенциальной энергии означает равновесие, а вопрос, является ли она экстремалью, связан лишь с вопросом об устойчивости этого равновесия (который далеко не всегда важен). Траектории стационарного действия отвечают возможному движению, независимо от того, минимально действие на такой траектории, максимально, или седловидно. То же можно сказать о геометрической оптике, где любая линия стационарного вермени (а не только минимального, как в простой формулировке принципа наименьшего времени Ферма) соответствует возможному движению светового луча неоднородной оптической среде. Есть системы, где вообще нет экстремалей, но стационарные точки существуют.

Способы нахождения условных экстремумов и условных стационарных точек (см. ниже) делают вариационное исчисление ещё более мощным орудием решения обеих задач.

Техника варьирования

Рассмотрим это сначала на простом частном примере, а затем на общем.

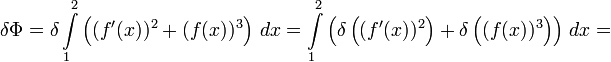
Теперь, чтобы δf(x) не стояло под знаком производной, мешающего вынести за скобки δf(x) из обоих членов (оставшееся в скобках суть вариационная производная), надо в первом слагаемом воспользоваться интегрированием по частям:

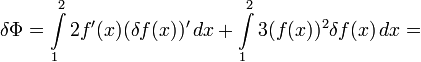
Теперь можно опять превратить сумму интегралов в один и вынести за скобки δf :

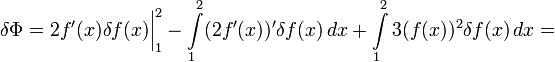
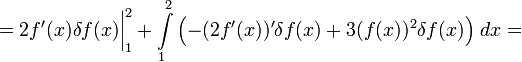
оставив граничный член 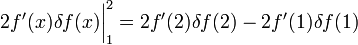, стоящим отдельно.

Таким образом, здесь под вариационной производной будем понимать вариационную производную по классу функций с фиксированными концами, которая (при поиске экстремали и в подобных задачах) будучи приравненной нулю, определяет поведение функции внутри отрезка . В этом смысле, для нашего примера имеем:

а необходимое условие экстремальности состоит в равенстве её нулю, то есть имеем уравнение для f :

Использование обобщённых функций

В этом разделе рассмотривается такой частный, но практически важный, случай применения обобщённых функций при решении вариационных задач, как использование дельта-функции Дирака.

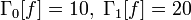
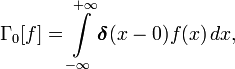
Для того, чтобы было удобно решать эту задачу, наложенные условия полезно записать в виде (в этом случае, суть функционалы). Не ограничиваясь этим, используя основное свойство дельта-функции, запишем Γ₀ и Γ₁ в интегральной форме:

Условные экстремумы

Условным экстремумом называется экстремум не на всей области определения функции (функционала), а на определённом её подмножестве, выделяемом специально наложенным условием (или условиями). Обычно, речь идёт о выделении этим условием (условиями) подмножества области определения с меньшей размерностью, что для конечномерных областей имеет определённый наглядный смысл, но для бесконечномерных (каковы обычно области определения функционалов) налагаемые условия приходится рассматривать лишь абстрактно (что теоретически не мешает иметь в виду полезную аналогию с конечномерным случаем).

Пусть надо найти экстремум функционала Φ[f] при некотором наложенном условии.

Как обычно, тривиальный случай, когда наложенное условие сводится к явному выражению чего-то через что-то (например, если известно, что 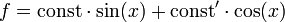), нет смысла специально рассматривать, так как это приводит просто к некоторому переписыванию функционала в новом виде (или даже к сведению функционала к функции конечного количества переменных).

Рассмотрения заслуживает случай, когда налагаемое в виде равенства нулю (в общем случае, константе) неких других функционалов (одного или нескольких), или наложение на искомую функцию уравнения, которому она должна удовлетворять.

Типичный случай первой задачи с одним наложенным условием — изопериметрическая задача (например, задача Дидонны). Примером второго типа условия может быть наложение в некоторых физических задачах требования подчинению уравнению непрерывности (для стационарных задач — его стационарного варианта ).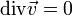

Основные виды задачи на условный экстремум, которые имеет смысл рассмотреть, таковы:

(Третий тип условия выписан здесь не в самом общем виде, но для наших целей этого достаточно.)

Третий же случай рассмотрим здесь для интегрального функционала . Тогда нахождение условного экстремума сводится сначала к варьированию функционала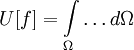

,

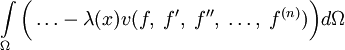
Таким образом, ключевой момент с точки зрения вариационного исчисления в нахождении условного экстремума третьего типа сводится к

Уравнение Эйлера — Лагранжа

Одним из основных классических результатов вариационного исчисления, имеющих огромное практическое значение, являются уравнения Эйлера — Лагранжа — дифференциальные уравнения, которым должна удовлетворять функция, являющаяся стационарной для довольно общего в своем классе и очень важного вида интегрального функционала (а значит и функция, на которой такой функционал достигает локального экстремума, тоже должна необходимо удовлетворять этим уравнениям).

Здесь приводится вывод уравнений Эйлера — Лагранжа с использованием производной функционала по направлению.

Вывод с использованием производной по направлению. Частный пример

Для гладких функций вещественной переменной или конечномерного векторного аргумента максимум и минимум заданной функции может быть найден путём нахождения точек, в которых производная обращается в нуль (по крайней мере, это необходимое условие экстремума). Аналогично решение гладких задач вариационного исчисления может быть получено путём решения соответствущего уравнения Эйлера — Лагранжа.

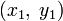
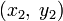
Чтобы проиллюстрировать этот процесс, рассмотрим сначала конкретную задачу нахождения кратчайшей кривой на плоскости, соединяющей две точки и . Длина кривой определяется выражением

для любого , близкого к 0. Следовательно, производная по (первая вариация A ) должна обращаться в нуль при . Таким образом,

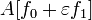
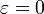
Из этого уравнения следует, что

Таким образом, экстремумом в нашей задаче являются отрезки прямых линий.

Вывод с использованием производной по направлению. Более общий случай

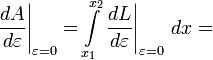
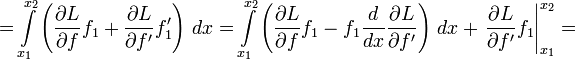
Наконец, в силу основной леммы вариационного исчисления можно заключить, что функция L должна удовлетворять уравнению Эйлера — Лагранжа

Уравнение Эйлера — Лагранжа является необходимым, но не достаточным условием наличия экстремума. Дополнительные условия формулируются отдельно.

Источник