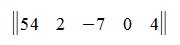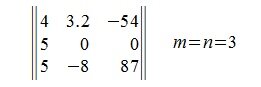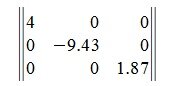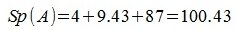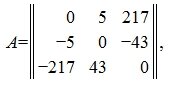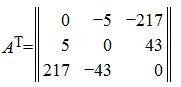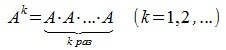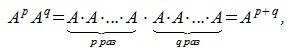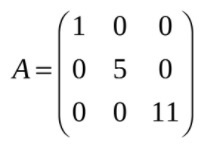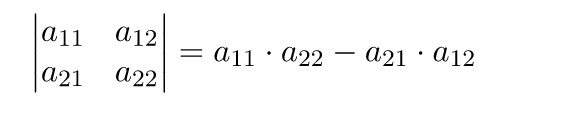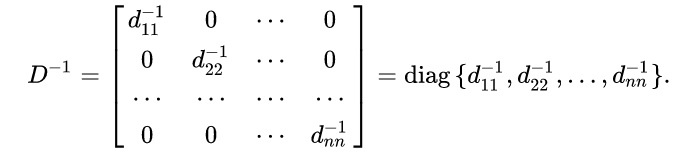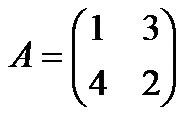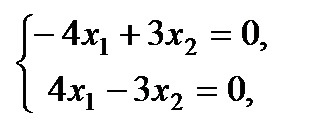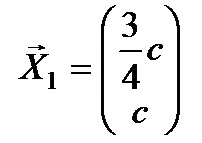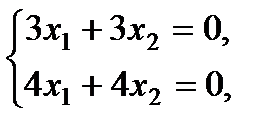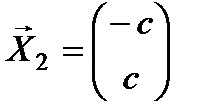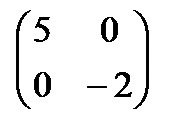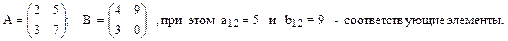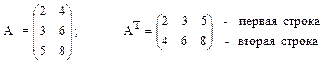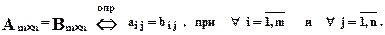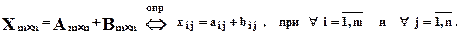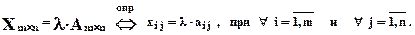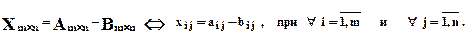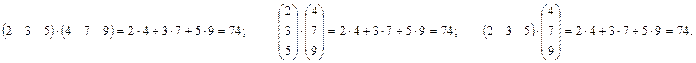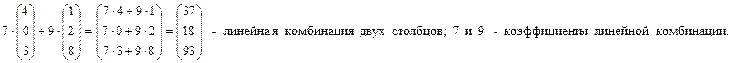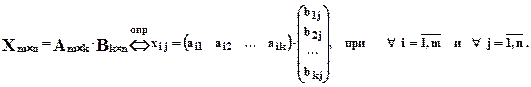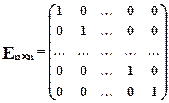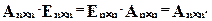Что такое главная и побочная диагонали квадратной матрицы

Матрицы. Виды матриц

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.

Матрица порядка m × n записывается в форме:

или (i=1,2. m; j=1,2. n).

Числа a_ij входящие в состав данной матрицы называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j— номер столбца.

Матрица строка

Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:

Матрица столбец

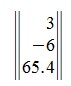
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например

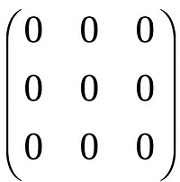
Нулевая матрица

Квадратная матрица

Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:

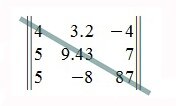
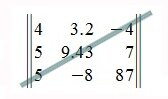
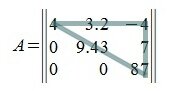
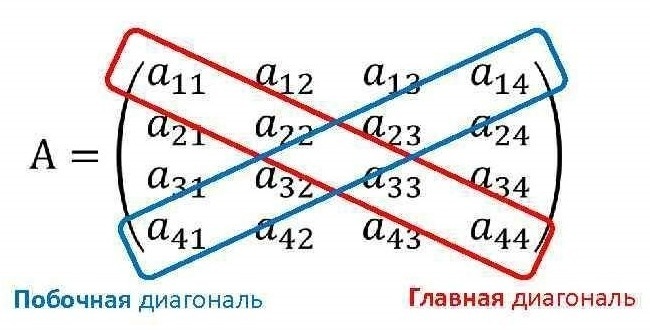
Главная диагональ матрицы

Побочная диагональ матрицы

Диагональная матрица

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:

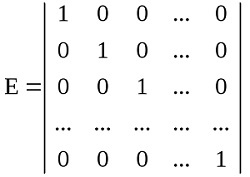
Единичная матрица

След матрицы

Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:

Верхняя треугольная матрица

Нижняя треугольная матрица

Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i T ).

Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).

Ядро или нуль пространство матрицы

Противоположная матрица

Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.

Кососимметричная (Кососимметрическая) матрица

Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:

В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.

Пример кососимметрической матрицы:

Разность матриц

Разностью C двух матриц A и B одинакового размера определяется равенством

Для обозначения разности двух матриц используется запись:

Степень матрицы

Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:

где E-единичная матрица.

Из сочетательного свойства умножения следует:

где p,q— произвольные целые неотрицательные числа.

Симметричная (Симметрическая) матрица

Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.

Для симметричных матриц имеет место равенство:

Источник

Матрицы: определение и основные понятия.

Определение матрицы

Количество строк и столбцов задают размеры матрицы.

Обозначение

A =		4	1	-7
		-1	0	2

Элементы матрицы

Элементы матрицы A_4×4:

A =		4	1	-7	2
		-1	0	2	44
		4	6	7	9
		11	3	1	5

Демонстрация нулевых и ненулевых строк матрицы:

Демонстрация нулевых и ненулевых столбцов матрицы:

4

1

-7

не не нулевой столбец

Диагонали матрицы

Демонстрация главной и побочной диагонали матрицы:

Источник

Диагональные матрицы: определение и свойства

Обновлено: 20 Июля 2021

Матрица — это прямоугольная таблица чисел, состоящая из определенного количества строк и столбцов. Существует множество матричных видов, и один из них — диагональный. Разберемся, что он из себя представляет.

	0	1	-7
	0	0	2

(МЕТОДИЧЕСКОЕ ПОСОБИЕ)

1.1. Основные понятия

Матрицей будем называть прямоугольную таблицу чисел, расположенных строками и столбцами; сами числа будем называть элементами матрицы , а число строк и число столбцов образуют размерность матрицы.

Приняты следующие обозначения.

— матрица размерностисодержит 2строки и 3столбца.

— матрица-строка (строка), содержит 1 строку.

— матрица-столбец (столбец), содержит 1столбец.

— матрица содержит mстрок и nстолбцов.

— означает, что i принимает все натуральные значения от 1 до n.

— нулевая матрица размерности .

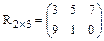
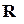
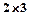
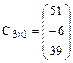
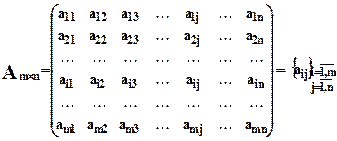
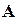
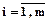
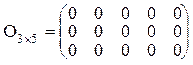
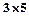
n строк и n столбцов.

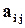
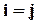
Элементы , у которых образуют ее главную диагональ,

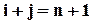
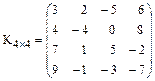
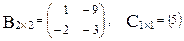
а если , то они образуют побочную диагональ.

— квадратная матрица 4-го порядка.

.

Квадратную матрицу будем называть треугольной, если все элементы, расположенные выше (либо ниже) главной диагонали равны нулю.

.

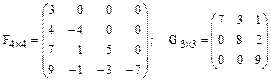
Квадратную матрицу будем называть диагональной, если все ее элементы, нерасположенные на главной диагонали равны нулю.

— диагональная матрица четвертого порядка.

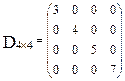
Диагональную матрицу будем называть единичной, если все элементы главнойдиагонали равны 1.

— единичная матрица пятого порядка.

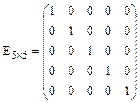
Элементы двух матриц будем называть соответствующими, если они имеют одинаковые индексы. Строки (столбцы) будем называть соответствующими, если они имеют одинаковый номер.

Транспонированием матрицы будем называть операцию замены всех столбцовсоответствующими строками

(всех строк соответствующими столбцами).

Матрицу будем называть симметрической (симметричной), если при транспонировании она не изменяется.

Из определения следует:

— симметрическая матрица может быть только квадратной;

— ее элементы расположены симметрично относительно главной диагонали.

.

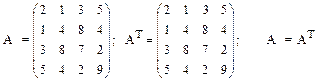
1.2. Действия с матрицами

Произведением матрицы А на скаляр l ( l× А )будем называтьновую матрицу ( Х )той же размерности, каждый элемент которой равен произведению соответствующего элемента данной матрицы на данный скаляр.

Из последних двух определений следует что разность двух матриц может быть найдена следующим образом:

Скалярным произведением двух строк (или двух столбцов, или строки и столбца), имеющих одинаковое количество элементов, будем называть число, равное сумме произведений всех соответствующих элементов.

Линейной комбинацией строк (столбцов) будем называть сумму произведений этих строк (столбцов) на вещественные числа (скаляры).

Сами числа при этом называют коэффициентами этой линейной комбинации.

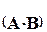
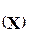
Произведением двух матриц будем называть новую матрицу , у которой каждый элемент х_ijравен скалярному произведению i — ойстроки первого сомножителя на j -й столбец второго сомножителя.

Из определения следуют свойства:

1.2.1. Количество столбцов матрицы-множимого должно быть равно количеству строк матрицы-множителя;

1.2.2. Матрица-произведение имеет столько строк, сколько их у матрицы-множимого и столько столбцов, сколько их у матрицы-множителя.

1.2.3. Умножение матриц не подчиняется переместительному закону.

1.2.4. Квадратные матрицы можно умножать только, если они имеют одинаковый порядок.

1.2.5. Умножение квадратной матрицы на единичную матрицу и слева и справа не изменяет данную матрицу.

;

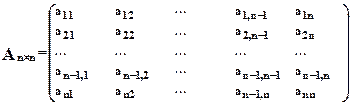
Две квадратные матрицы будем называть взаимно обратными, если их произведение равно единичной матрице.

Источник

Главной или побочной диагонали матрицы

Существует множество задач, в которых необходимо использовать элементы главной или побочной диагонали матрицы (эти понятия имеют смысл только для квадратных матриц!).

Пусть дана матрица а(4,4).

a₁₁, a₂₂, a₃₃, a₄₄ – элементы главной диагонали матрицы. На главной диагонали индексы строки и столбца равны, то есть i = j. Элемент главной диагонали можно обозначать как a[i,i].

У элементов матрицы, лежащих выше главной диагонали, i j.

a₁₄, a₂₃, a₃₂, a₄₁ – элементы побочной диагонали матрицы. На побочной диагонали сумма индексов строки и столбца постоянна и на единицу больше размера матрицы, т. е. для матрицы a(4, 4) сумма индексов i + j = 5, поэтому элемент побочной диагонали можно обозначать как a[i,5 – i].

У элементов a[i, j], лежащих выше побочной диагонали сумма индексов i + j 5.

Задача 1. Найти сумму элементов, расположенных на главной диагонали матрицы a.

Задача 2. Найти сумму элементов матрицы а, расположенных выше ее главной диагонали.

var к, i, j : integer;

writeln (¢введите матрицу d¢);

в которой он находится>

Описание функции содержится в главной программе после раздела описания переменных (var) и перед началом (begin) программы.

В общем виде функция записывается следующим образом:

function имя(формальные параметры) :тип результата;

Раздел описаний

Begin

Раздел операторов

Формальные параметры – это наименования переменных (аргументы описываемой функции), через которые передаются входные данные из программы в функцию. Формальными параметрами функции, как правило, являются параметры – значения.

Само имя функции представляет собой идентификаторпараметр, значение которого после окончания работы функции равно результату вычисления. Тип результата (функции) указывается следом за списком параметров – после закрывающей скобки этого списка и двоеточия.

В разделе операторов функции обязательно должен присутствовать хотя бы один оператор присваивания, в котором переменной с именем, совпадающим с именем функции, присваивается определенное значение, тип которого совпадает с типом результата (функции). Если такого присваивание в разделе операторов функции не выполнено, то функция не возвращает никакого результата (точнее, возвратит произвольный результат).

Например, описания вычисления функции тангенса угла:

function tg(x:real): real;

Вызов и выполнение функции производится при вычислении указателя функции:

имя функции(фактические параметры ).

При этом вызов функции необходимо делать непосредственно внутри выражения, подобно тому, как используются стандартные встроенные функции, например синус sin(x). Фактические и формальные параметры должны согласовываться

¾ по порядку следования,

Например, вызов ранее описанной функции tg можно произвести так:

После выполнения функции выработанный ею результат используется в качестве значения указателя функции в том выражении, в котороe входит этот указатель. При вызове функции передача фактических параметров производится так же, как и при вызове процедуры.

Пример. Заданы стороны двух треугольников MNK (стороны m, n, k) и PLF (стороны p, l, f ). Переменной s присвоить значение –1, если площадь треугольника MNK меньше или равнa площади треугольника PLF, и значение 1 в противном случае.

Вычисление площади треугольников по формуле Герона оформить в виде функции pl.

Примечание. Формула Герона для вычисления площади треугольника со сторонами a, b, c:

,

где , где p – полупериметр треугольника.

var m, n, k, l, p, f, h, q: real;

function pl(a, b, c: real): real;

writeln(‘Введите стороны m, n, k, p, l, f’);

При передаче в функцию массива фактическим параметром является имя массива. Обратим внимание на то, что в заголовке функции для указания типов формальных параметров могут использоваться только имена типов, но не их описания.

Нельзя записать так:

function sum(a: array[1..5] of real; var : real):real;

Пример. Пусть заданы два вектора а(8) и b(12). Вычислить для каждого вектора произведение его элементов.

function prl(var x: vect; n: integer): real;

Пример выполнения задания 7

где X_k – наибольшее из значений элементов K – го столбца матрицы A.

Вычисление наибольшего значения оформить в виде функции.

type matr = array[1..4,1..4] of real;

function max(y:matr; k: integer): real;

writeln(‘введите матрицу a(4,4)’);

Тема 8

Организация программ

С использованием процедур

Довольно часто, уже на этапе разработки алгоритма программы, можно обнаружить, что некоторые одинаковые или очень похожие действия в программе должны выполняться несколько раз. Текст программы, реализующей такой алгоритм, будет содержать последовательность одинаковых операторов.

Избежать дублирования операторов можно, если оформить повторяющуюся последовательность как процедуру и в том месте программы, где надо выполнить эти инструкции, указать ее имя.

В Турбо Паскале процедурой называется часть программы, имеющая имя и предназначенная для решения определенной задачи (вместо термина «процедура», часто используют термин подпрограмма).

Описание процедуры включает заголовок и тело процедуры. Заголовок состоит из зарезервированного слова procedure, идентификатора (имени) процедуры и заключенного в круглые скобки списка формаль­ных параметров с указанием типа каждого параметра.

В общем виде описание процедуры выглядит так:

procedure имя (формальные параметры);

Имя процедуры должно быть уникальным и не должно встречаться в разделе операторов данной процедуры.

Нетрудно заметить, что структура процедуры копирует структуру программы в целом, т. е. состоит из заголовка, раздела описаний и раз­дела операторов. Различия лишь в заголовках и в том, что в конце про­цедуры ставится точка с запятой вместо точки в конце программы. Процедура помещается в основной программе после раздела описания переменных и перед разделом операторов основной программы.

Все переменные, представленные в разделе описаний основной программы, называются глобальными. Они действуют как в разделе операторов основной программы, так и в любой процедуре. Переменные, представленные в разделе описаний процедуры, называются локальными. Они действуют только в рамках процедуры и недоступны операторам основной программы.

Формальные параметры – это наименование фиктивных переменных, через которые передается информация из программы в процедуру (входные параметры) либо из процедуры в программу (выходные параметры). Выходным параметрам присваиваются результаты вычислений.

Описание процедуры, расположенное в описательной части программы, само по себе никакого действия не производит. Выполнение программы начинается с выполнения раздела операторов основной программы. Для обращения к процедуре применяется оператор вызова процедуры, который имеет вид:

Имя процедуры(список фактических параметров).

Фактические параметры отделяются друг от друга запятыми и являются реальными объектами программы, замещающими в разделе операторов процедуры формальные параметры. Описание фактических параметров содержится в разделе описаний переменных основной программы.

При вызове процедуры компьютер производит следующие действия. Сначала устанавливает взаимно однозначное соответствие между фактическими и формальными параметрами.

Соответствие между фактическими и формальными параметрами должно быть следующим:

– число фактических параметров должно быть равно числу формальных параметров;

– соответствующие фактические и формальные параметры долж­ны совпадать по порядку следования и по типу.

Данные из основной программы поступают в процедуру. Затем управление передается процедуре. Результаты выполнения процедуры передаются в основную программу и управление передается на оператор, следующий за вызовом процедуры. Соответствующие формальные и фактические пара­метры во избежание путаницы обычно обозначают разными буквами.

Параметры

Параметры, перед которыми отсутствует зарезервированное слово var и за которыми следует тип, называются параметрами-значениями. Например, в описании

procedure korrect (s, к : real; x : integer);

s, k, x –параметры-значения. Фактический параметр, соответствующий параметру-значению, может быть выражением соответствующего типа, например:

Изменение формальных параметров-значений не влияет на значе­ния соответствующих фактических параметров.

Параметры, перед которыми следует ключевое слово var и за кото­рым следует тип, называются параметрами-переменными. Например, в описании

procedure obr(var s, k: real; var x : integer);

s, k, x – параметры-переменные. Фактический параметр, соответствую­щий параметру-переменной, может быть только переменной, например:

где а, b – переменные вещественного типа, а k –целого типа.

Любые изменения в значении формального параметра-переменной отражаются на фактическом параметре.

Параметр-переменная используется в том случае, если значение должно быть передано из процедуры в вызывающий блок.

Пример. Решить два квадратных уравнения и ,

считая, что его дискриминант неотрицателен.

procedure sq( a, b, с : real; var xl, x2: real);

Источник