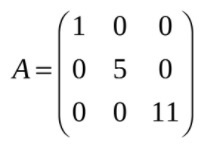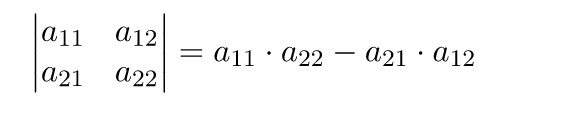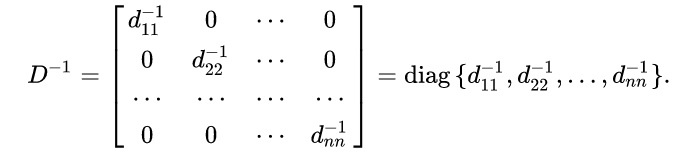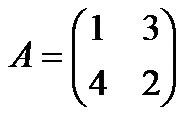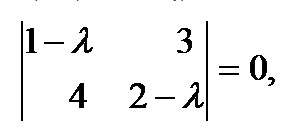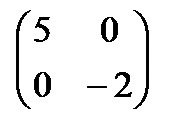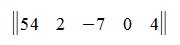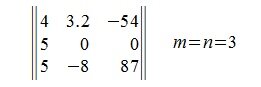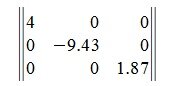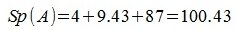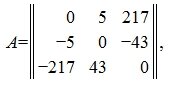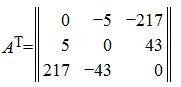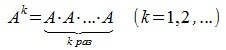Что такое главная и побочная диагональ матрицы

Матрицы: определение и основные понятия.

Определение матрицы

Количество строк и столбцов задают размеры матрицы.

Обозначение

A =		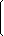4	1	-7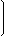
		-1	0	2

Элементы матрицы

Элементы матрицы A_4×4:

A =		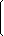4	1	-7	2
		-1	0	2	44
		4	6	7	9
		11	3	1	5

Демонстрация нулевых и ненулевых строк матрицы:

Демонстрация нулевых и ненулевых столбцов матрицы:

4

1

-7

не не нулевой столбец

Диагонали матрицы

Демонстрация главной и побочной диагонали матрицы:

Источник

Диагональные матрицы: определение и свойства

Обновлено: 20 Июля 2021

Матрица — это прямоугольная таблица чисел, состоящая из определенного количества строк и столбцов. Существует множество матричных видов, и один из них — диагональный. Разберемся, что он из себя представляет.

Что такое диагональная матрица

У диагональной матрицы элементы, расположенные вне главной диагонали, равны нулю.

Напомним, что матрица считается квадратной, если количество строк равно количеству столбцов (m = n).

Особенности и свойства

Для начала нужно понять, что такое матричный определитель.

Определитель (детерминант) — это некоторая величина, с которой можно сопоставить любую квадратную матрицу.

Определитель А = (2×2), к примеру, вычисляется по формуле:

Из этого следует свойство №1: определитель диагональной матрицы равен произведению ее диагональных элементов.

Свойство №2: обратная матрица для диагональной равна:

Свойство №3: ранг равен количеству ненулевых диагональных элементов.

Главная и побочная диагонали

Побочной диагональю называют диагональ элементов от правого верхнего угла до нижнего левого. Эти диагонали параллельны друг другу.

Частные случаи диагональных матриц

Существуют три основных подвида: единичная, нулевая, скалярная.

Единичная матрица

У единичной матрицы все диагональные элементы равны единице.

В формулах ее обозначают буквой Е.

Нулевая матрица

В нулевой матрице все элементы, в том числе диагональные, равны нулю.

В формулах ее обозначают цифрой 0.

Скалярная матрица

В скалярной матрице все элементы на главной диагонали равны друг другу.

В некоторых случаях говорят, что скалярная матрица — это произведение скаляра на единичную матрицу Е. В ней диагональные элементы могут быть как положительными, так и отрицательными.

Примеры решения диагональных матриц

Иногда недиагональная матрица может быть приведена к диагональному виду.

Условие: дана матрица А

Задача: привести к диагональному виду.

Решение: характеристическое уравнение равно

Таким образом, диагональная матрица имеет вид:

Изучение данных математических объектов имеет свои подводные камни. Если у вас нет времени на учебу, Феникс.Хелп может помочь вам с решением контрольных, самостоятельных и иных проверочных работ.

Источник

Pascal: Занятие № 10. Двумерный массив в Pascal

Двумерный массив в Pascal

Матрица или двумерный массив – это прямоугольная таблица чисел (или других элементов одного типа). Каждый элемент матрицы имеет два индекса (номер строки и номер столбца).

Исходные данные для решения многих задач можно представить в табличной форме:

Таблица результатов производственной деятельности нескольких филиалов фирмы может быть представлена так:

zavod1: array [1..4] of integer; zavod2: array [1..4] of integer; zavod3: array [1..4] of integer;

Или в виде двумерного массива так:

var A: array[1..3,1..4] of integer; begin

begin var a := new integer[3,4]; <. >end.

Описание, ввод и вывод элементов двумерного массива

Варианты описания двумерного массива (традиционный pascal)

const N = 3; M = 4; var A: array[1..N,1..M] of integer;

const M=10; N=5; type matrix=array [1..M, 1..N] of integer; var A: matrix;

for i:=1 to N do for j:=1 to M do begin write(‘A[‘,i,’,’,j,’]=’); read ( A[i,j] ); end;

for var i:=0 to a.RowCount-1 do for var j:=0 to a.ColCount-1 do a[i,j]:=readinteger;

var a := MatrRandomInteger(3,4,0,10); // целые числа в диапазоне от 0 до 10 var a1 := MatrRandomReal(3,4,1,9) // веществ. числа в диапазоне от 1 до 9

Следующий фрагмент программы выводит на экран значения элементов массива по строкам:

for i:=1 to N do begin for j:=1 to M do write ( A[i,j]:5 ); writeln; end;

begin var a := MatrRandomInteger(3,4,0,10); var a1 := MatrRandomReal(3,4,1,9); a.Println; a1.Println(6,1) // 6 позиций всего на вывод, 1 знак после десят. запятой end.

Рассмотрим следующую задачу: Получены значения температуры воздуха за 4 дня с трех метеостанций, расположенных в разных регионах страны:

	0	1	-7
	0	0	2

Т.е. запись показаний в двумерном массиве выглядела бы так:

Или в pascalabc.NET:

var t := Matr(3,4,-8,-14,-19,-18,25,28,26,20,11,18,20,25); t.Println;

Объявление двумерного массива:

var t: array [1..3, 1..4] of integer;

Самостоятельно подумайте, как находится сумма элементов массива pascal.

Методы матриц для работы со строками и столбцами:

begin var a := MatrRandomInteger(3,4); a.Println; a.Row(0).Sum.Println(); a.Row(1).Average.Println; a.Row(2).Product.Println; a.Col(0).Min.Println; a.Col(1).Max.Println; end.

Главная и побочная диагональ при работе с двумерными матрицами в Pascal

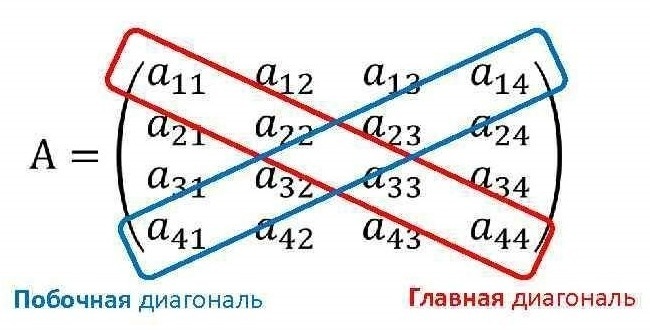
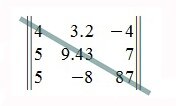
Главная диагональ квадратной матрицы n x n (т.е. той, у которой количество строк равно количеству столбцов) проходит с верхнего левого угла матрицы (элемент 1,1) до правого нижнего угла матрицы (элемент n,n).

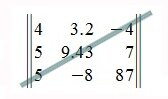
Побочная диагональ квадратной матрицы n x n проходит с нижнего левого угла матрицы (элемент n,1) до правого верхнего угла матрицы (элемент 1,n).

Формулу поиска элементов диагоналей проще всего искать, нарисовав элементы матрицы:
Если индексы начинаются с единицы (традиционный Паскаль):

Если индексы начинаются с нуля (pascalAbc.NET):

где n — размерность квадратной матрицы

Побочная диагональ матрицы в pascalAbc.Net имеет формулу:
n=i+j+1

где n — размерность квадратной матрицы

var i,j,n:integer; a: array[1..100,1..100]of integer; begin randomize; writeln (‘введите размерность матрицы:’); readln(n); for i:=1 to n do begin for j:=1 to n do begin a[i,j]:=random(10); write(a[i,j]:3); end; writeln; end; writeln; for i:=1 to n do begin for j:=1 to n do begin if (i=j) or (n=i+j-1) then a[i,j]:=0; write(a[i,j]:3) end; writeln; end; end.

var A:array[1..5,1..5] of integer; i,j:integer; sum,sum1,sum2:integer; begin randomize; for i:=1 to 5 do for j:=1 to 5 do A[i,j]:=random(10); write (‘Исходный массив A: ‘); for i:=1 to 5 do begin writeln; for j:=1 to 5 do write (A[i,j]:2,’ ‘); end; sum1:=0; for i:=1 to 5 do for j:=1 to 5 do if (i-j=1) then sum1:=sum1+A[i,j]; sum2:=0; for i:=1 to 5 do for j:=1 to 5 do if (j-i=1) then sum2:=sum2+A[i,j]; sum:=sum1+sum2; writeln; writeln(‘Сумма = ‘,sum); end.

Рассмотрим еще один пример работы с двумерным массивом.

var index1,index2,i,j,N,M:integer; s,min,f:real; a:array[1..300,1..300] of real; begin N:=10; M:=5; for i:=1 to N do begin for j:=1 to M do begin a[i,j]:=random(20); s:=s+a[i,j]; write(a[i,j]:3); end; writeln; end; f:=s/(N*M); writeln(‘srednee znachenie ‘,f); min:=abs(a[1,1]-f); for i:=1 to N do begin for j:=1 to M do begin if abs(a[i,j]-f)

Источник

Матрицы. Виды матриц

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.

Матрица порядка m × n записывается в форме:

или (i=1,2. m; j=1,2. n).

Числа a_ij входящие в состав данной матрицы называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j— номер столбца.

Матрица строка

Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:

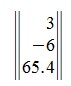
Матрица столбец

Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например

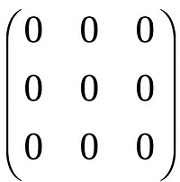
Нулевая матрица

Квадратная матрица

Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:

Главная диагональ матрицы

Побочная диагональ матрицы

Диагональная матрица

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:

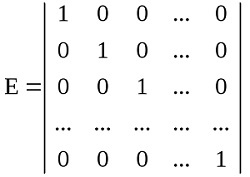
Единичная матрица

След матрицы

Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:

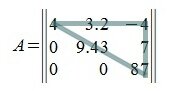
Верхняя треугольная матрица

Нижняя треугольная матрица

Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i T ).

Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).

Ядро или нуль пространство матрицы

Противоположная матрица

Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.

Кососимметричная (Кососимметрическая) матрица

Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:

В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.

Пример кососимметрической матрицы:

Разность матриц

Разностью C двух матриц A и B одинакового размера определяется равенством

Для обозначения разности двух матриц используется запись:

Степень матрицы

Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:

где E-единичная матрица.

Из сочетательного свойства умножения следует:

где p,q— произвольные целые неотрицательные числа.

Симметричная (Симметрическая) матрица

Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.

Для симметричных матриц имеет место равенство:

Источник

Математика для чайников. Матрицы и основные действия над ними

Определение матрицы

Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.

Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.

Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.

Операции сложения и вычитания матриц

Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.

Вычитание выполняется по аналогии, только с противоположным знаком.

Умножение матрицы на число

На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:

Операция умножения матриц

И пример с реальными числами. Умножим матрицы:

Операция транспонирования матрицы

Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:

Определитель матрицы

Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!

Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.

Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.

А если матрица три на три? Тут уже посложнее, но справиться можно.

Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

К счастью, вычислять определители матриц больших размеров на практике приходится редко.

Источник