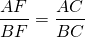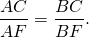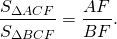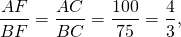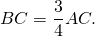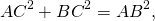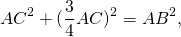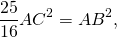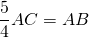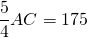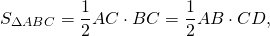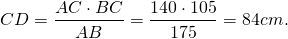Что такое гипотенуза и биссектриса
Треугольник. Важные факты о высоте, биссектрисе и медиане
Определения
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
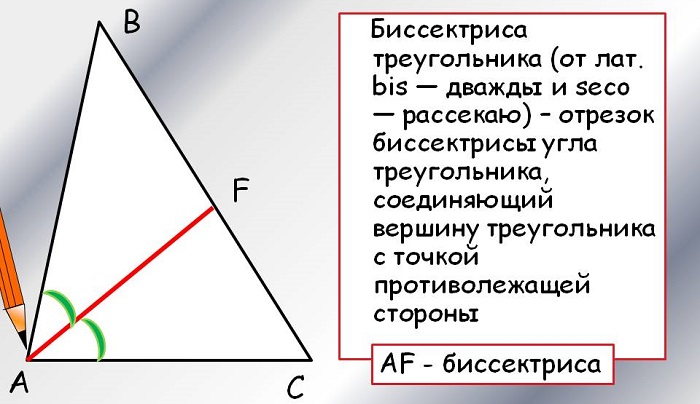
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Теорема
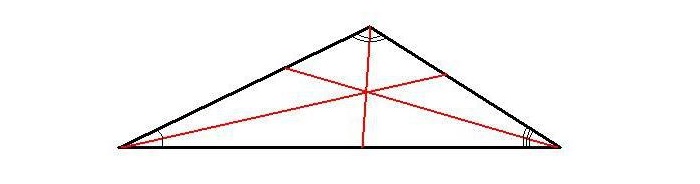
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема
Доказательство
Для других медиан треугольника \(ABC\) требуемое свойство доказывается аналогично.
Теорема
Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).
Доказательство
Теорема
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.
Доказательство
Теорема
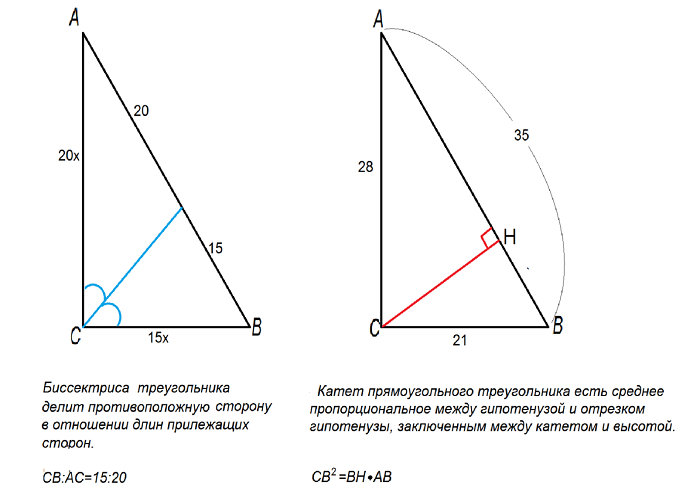
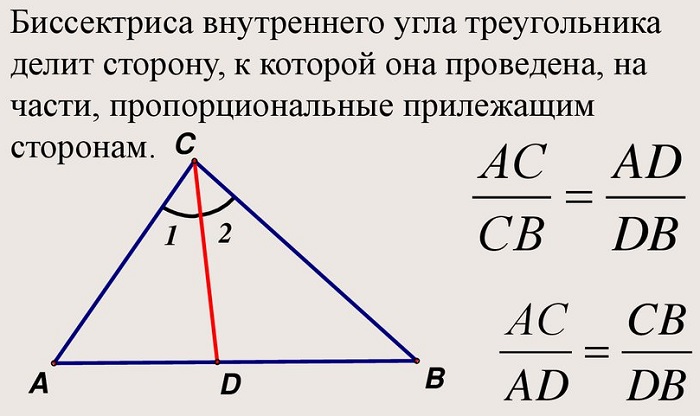
Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:
Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.
Доказательство
Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть \[\dfrac
Теорема
Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Верно и обратное: если точка лежит на биссектрисе угла, то она равноудалена от его сторон.
Доказательство
Свойства биссектрисы прямоугольного треугольника
В данной публикации мы рассмотрим основные свойства биссектрисы прямоугольного треугольника, проведенной из прямого и острого углов, а также разберем примеры решения задач по данной теме.
Примечание: напомним, что прямоугольным называется треугольник, в котором один из углов прямой (т.е. равен 90°), а два остальных – острые ( Содержание скрыть
Свойства биссектрисы прямоугольного треугольника
Свойство 1
Если в прямоугольном треугольнике известны катеты, то длину биссектрисы, проведенной из прямого угла к гипотенузе, можно вычислить по формуле:
Свойство 2
Длину биссектрисы в прямоугольном треугольнике, проведенную из острого угла к противолежащему катету, можно вычислить по формуле:
Также можно использовать другую формулу, если известны все три стороны треугольника:
Примечания:
Примеры задач
Задача 1
Найдите длину биссектрисы, которая проведена к гипотенузе прямоугольного треугольника, если известно, что его катеты равны 21 и 28 см.
Решение
Воспользуемся формулой, приведенной в Свойстве 1, подставив в нее известные значения:
Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Вычислите длину биссектрисы, проведенной к катету с наименьшей длиной.
Решение
Пример катеты за “a” (9 см) и “b” (12 см).
Для начала найдем гипотенузу треугольника (c), воспользовавшись теоремой Пифагора, согласно которой квадрат гипотенузы равняется сумме квадратов катетов:
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, c = 15 см.
Теперь мы можем применить формулу, рассмотренную в Свойстве 2 для нахождения длины биссектрисы:
Треугольники
Виды треугольников
Треугольник называется равнобедренным, если у него две сторны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.
Треугольник, у которого все сторны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.
Треугольник называется остроугольным, если все три его угла — острые, то есть меньше 90°.
Треугольник называется тупоугольным, если один из его углов — тупой, то есть больше 90°.
Основные линии треугольника
Медиана
Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.
Свойства медиан треугольника
Биссектриса
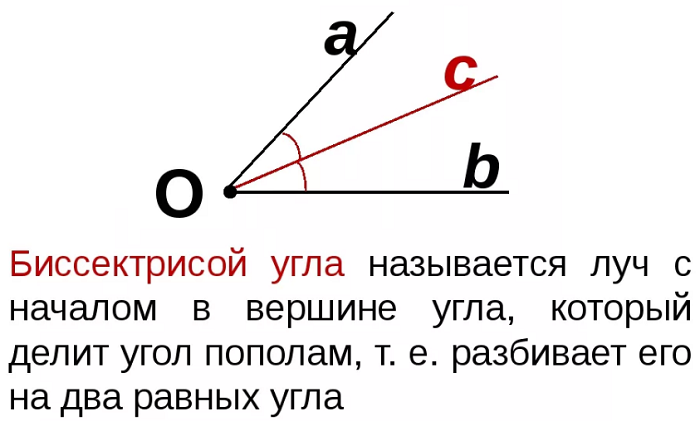
Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Свойства биссектрис треугольника
Высота
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.
Свойства высот треугольника
Срединный перпендикуляр
Свойства серединных перпендикуляров треугольника
Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Формулы и соотношения
Признаки равенства треугольников
Два треугольника равны, если у них соответственно равны:
Признаки равенства прямоугольных треугольников
Два прямоугольных треугольника равны, если у них соответственно равны:
Подобие треугольников
Два треугольника подобны, если выполняется одно из следующих условий, называемых признаками подобия:
В подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны.
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов, причем коэффициент пропорциональности равен диаметру описанной около треугольника окружности:
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Формулы площади треугольника
Биссектриса делит гипотенузу
В каком отношении биссектриса делит гипотенузу?
По свойству биссектрисы треугольника биссектриса делит третью сторону на отрезки, пропорциональные двум другим сторонам.
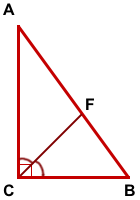
Поскольку биссектриса делит площадь треугольника пропорционально прилежащим сторонам, то биссектриса, проведённая к гипотенузе, делит площадь прямоугольного треугольника пропорционально катетам:
Биссектриса прямоугольного треугольника делит гипотенузу на отрезки 100 см и 75 см. Найти, на какие части делит гипотенузу высота треугольника.
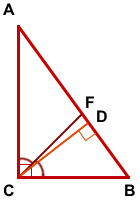
CF — биссектриса, AF=100 см, BF=75 см,
По свойству биссектрисы треугольника
(извлечь из обеих частей квадратный корень можем в силу того, что AC>0, AB>0).
AB=AF+BF=175 см. Таким образом,
и AC=140 см, BC=105 см.
2 Comments
Требовалось найти одно, нашли другое. Несостыковочка(
Базовым понятием и одним из наиболее интересных и полезных объектов школьной математики является биссектриса. С её помощью доказываются многие положения планиметрии, упрощается решение задач.
Известные свойства позволяют рассматривать геометрические фигуры с разных точек зрения. Появляется вариативность при выборе пути доказательств.
Становится возможным использование инструмента алгебры, например, свойство пропорции, нахождение неизвестных величин, решение алгебраических уравнений при рассмотрении геометрических вопросов.
Что такое биссектриса в геометрии
Рассматривают луч, выходящий из вершины угла или его часть (отрезок), который делит угол пополам. Такой луч (или, соответственно, отрезок) называется биссектрисой.
Часто для треугольников определение немного сужают, говоря об отрезке, соединяющем вершину угла, делящем его пополам, с точкой на противолежащей стороне. При этом рассматривается внутренняя область фигуры.
В то же время, часто при решении задач используются прямые, делящие внешние углы на два равных.
Биссектриса прямоугольного треугольника
Для прямоугольного треугольника одна из биссектрис образует равные углы, величины которых хорошо просчитываются (45 градусов).
Это помогает вычислять углы при решении задач, связанных с фигурами, которые можно представить в виде прямоугольных треугольников или прямоугольников.
Свойства биссектрисы треугольника
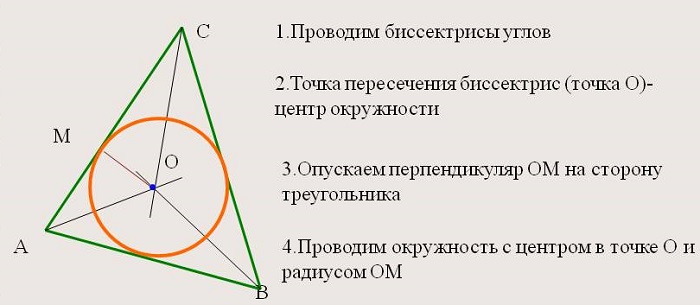
1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.
2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон.
Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.
Благодаря этому утверждению, легко доказывается следующее правило:
Площадь описанного многоугольника равна:
где p – полупериметр, а r – радиус вписанной окружности.
Это позволяет находить решение не только планиметрических, но и стереометрических задач.
Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;
3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.
Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;
4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.
В этом случае основание параллельно внешней биссектрисе.
Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;
5. Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;
6. У правильного треугольника все внешние биссектрисы параллельны сторонам;
7. Выделяют несколько особенностей, среди которых есть следующая теорема:
«Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам».
Обратное утверждение («Прямая делит сторону на отрезки, пропорциональные двум другим сторонам») выражает признаки того, что рассматриваемая линия является внутренней биссектрисой;
8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.
Все формулы биссектрисы в треугольнике
В зависимости от исходных данных, длина биссектрисы, проведённой к стороне C, lc, равна:
Примеры решения задач
Задача №1
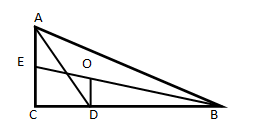
В ΔABC ∠C = 90°, проведена биссектриса острого угла. Отрезок, соединяющий её основание с точкой пересечения медиан, перпендикулярен катету. Найти углы заданной фигуры.
Пусть ∠ACB = 90°, AD – биссектриса, BE – медиана, O – точка пересечения медиан, OD⊥BC.
Тогда OE : OB = 1 : 2по свойству медиан.
Так как OD⊥BC, то ODIIOC, следовательно, ΔBOD ∼ ΔBEC по второму признаку подобия, поэтому, по свойству подобных фигур, CD : DB = 1 : 2.
Это означает, что CA : AB = 1 : 2.
Так как катет равен половине гипотенузы, то ∠ABC = 30°, откуда ∠CAB = 60°.
Задача №2
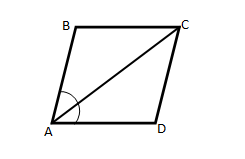
Диагональ параллелограмма делит его острый угол пополам. Доказать, что этот параллелограмм является ромбом.
Так как ABCD – параллелограмм, то ∠DAC = ∠ACB, как накрест лежащие при параллельных прямых AD, BC и секущей AC.
По условию, ∠DAC = ∠ACB = ∠BAC, поэтому ΔACB равнобедренный, то есть AB = BC, следовательно, ABCD – ромб.