Что такое достоверное событие

1.2.1. Виды событий

Одно из базовых понятий тервера уже озвучено выше – это событие. События бывают достоверными, невозможными и случайными.

1) Достоверным называют событие, которое в результате испытания (осуществления определенных действий, определённого комплекса условий) обязательно произойдёт. Например, в условиях земного тяготения подброшенная монета непременно упадёт вниз.

3) И, наконец, событие называется случайным, если в результате испытания оно может, как произойти, так и не произойти, при этом должен иметь место принципиальный критерий случайности: случайное событие – есть следствие случайных факторов, воздействие которых предугадать невозможно или крайне затруднительно. Пример: в результате броска монеты выпадет «орёл». В рассмотренном случае случайные факторы – это форма и физические характеристики монеты, сила и направление броска, сопротивление воздуха и т.д.

Подчёркнутый критерий случайности очень важен – так, карточный шулер может очень ловко имитировать случайность и давать выигрывать клиенту, но ни о каких случайных факторах, влияющих на итоговый результат, речи не идёт.

Любой результат испытания называется исходом, который, собственно и представляет собой появление определённого события. В частности, при подбрасывании монеты возможно 2 исхода (случайных события): выпадет орёл, выпадет решка. Естественно, подразумевается, что данное испытание проводится в таких условиях, что монета не может встать на ребро или, скажем, зависнуть в невесомости.

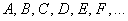
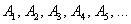
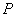
События (любые) обозначают большими латинскими буквами либо теми же буквами с подстрочными индексами, например: . При этом стараются избегать буквы , которая зарезервирована под другие нужды.

Запишем следующие случайные события:

– в результате броска монеты выпадет «орёл»;
– в результате броска игральной кости (кубика) выпадет 5 очков;
– из карточной колоды будет извлечена карта трефовой масти.

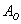
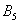
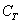
Да, события прямо так и записывают в практических задачах, при этом в уместных случаях удобно использовать «говорящие» подстрочные индексы (хотя можно обойтись и без них).
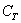
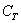
И следует в третий раз подчеркнуть, что случайные события обязательно удовлетворяют вышеприведённому критерию случайности. В этом смысле особо показателен 3-й пример: если из колоды изначально удалить все карты трефовой масти, то событие становится невозможным. Наоборот, если испытателю известно, что, например, дама треф лежит снизу, то он при желании может сделать событие достоверным =) Таким образом, в данном примере предполагается, что карты хорошо перемешаны и их «рубашки» неразличимы, т.е. колода не является краплёной.

Важной характеристикой случайных событий является их равновозможность. Два или бОльшее количество событий называют равновозможными, если ни одно из них не является более возможным, чем другое. Например:

– выпадение орла или решки при броске монеты;
– выпадение 1, 2, 3, 4, 5 или 6 очков при броске игрального кубика;
– появление трефы, пики, бубны или червы при случайном извлечении карты из полной колоды.

При этом предполагается, что монета и кубик однородны и имеют геометрически правильную форму, а колода хорошо перемешана и «идеальна» с точки зрения неразличимости рубашек карт.

Могут ли быть те же события НЕ равновозможными? Легко. Так, если у монеты или кубика смещён центр тяжести, то гораздо чаще будут выпадать вполне определённые грани. Если кто-то ловко спрятал в рукаве туза треф, то становится менее возможным, что оппоненту будет сдана трефа, и, главное, менее возможно, что будет сдан туз.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

ДОСТОВЕРНОЕ СОБЫТИЕ

— событие, которое априори должно обязательно произойти. Точнее, если W= — пространство элементарных исходов, то событие А, наступающее вместе с любым из элементарных исходов со, наз. Д. с. и, очевидно, должно совпадать со всем пространством W. Поэтому естественно приписать Д. с. вероятность, равную 1:

Дополнительным к Аявляется невозможное событие.

Смотреть что такое «ДОСТОВЕРНОЕ СОБЫТИЕ» в других словарях:

Достоверное Событие — См. Событие случайное Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов

достоверное событие — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN certain eventsure event … Справочник технического переводчика

достоверное событие — būtinasis įvykis statusas T sritis fizika atitikmenys: angl. certain event vok. sicheres Ereignis, n rus. достоверное событие, n pranc. événement certain, m … Fizikos terminų žodynas

достоверное событие — Syn: уверенность, достоверность Ant: неуверенность, недостоверность … Тезаурус русской деловой лексики

Почти достоверное событие — В теории вероятности, говорят, что событие почти достоверно или что оно произойдет почти наверняка, если это произойдет с вероятностью 1. Понятие является аналогом понятия «почти всюду» в теории меры. В то время, как во многих основных… … Википедия

ВЕРОЯТНОСТЕЙ ТЕОРИЯ — занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним… … Энциклопедия Кольера

ВЕРОЯТНОСТЕЙ ТЕОРИЯ — раздел математики, в к ром строят и изучают матем. модели случайных явлении. Случайность присуща в той или иной степени подавляющему большинству протекающих в природе процессов. Обычно она присутствует там, где существ. влияние на ход процесса… … Физическая энциклопедия

Вероятностей теория — математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных каким либо образом с первыми. Утверждение о том, что какое либо событие наступает с Вероятностью,… … Большая советская энциклопедия

ВЕРОЯТНОСТЕЙ ТЕОРИЯ — математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных к. л. образом с первыми. Утверждение о том, что к. л. событие наступает с вероятностью, равной, напр., 1/2, еще не… … Математическая энциклопедия

Источник

Теория вероятностей, формулы и примеры

Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.

Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.

Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным.

Ну, скажем, смотрим на тучи и понимаем, что дождь — вполне себе вероятное событие. А если светит яркое солнце, то дождь — маловероятное или невероятное событие.

Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории:

Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.

Формулы по теории вероятности

Теория вероятности изучает события и их вероятности. Если событие сложное, то его можно разбить на простые составные части — так легче и быстрее найти их вероятности. Рассмотрим основные формулы теории вероятности.

Случайные события. Основные формулы комбинаторики

Классическое определение вероятности

Вероятностью события A в некотором испытании называют отношение:

P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A

Таким образом, вероятность любого события удовлетворяет двойному неравенству:

Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?

Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:

Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное.

Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?

Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).

Геометрическое определение вероятности

Геометрическая вероятность события А определяется отношением:

P(A)= m(A)/m(G), где m(G) и m(A) — геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно

Чаще всего, в одномерном случае речь идет о длинах отрезков, в двумерном — о площадях фигур, а в трехмерном — об объемах тел.

Пример. Какова вероятность встречи с другом, если вы договорились встретиться в парке в промежутке с 12.00 до 13.00 и ждете друг друга 5 минут?

У нас есть отличные курсы по математике для учеников с 1 по 11 классы — приглашаем на вводный урок!

Сложение и умножение вероятностей

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

Если случайные события A₁, A₂. A_n образуют полную группу несовместных событий, то справедливо равенство:

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Формула полной вероятности и формула Байеса

По теореме умножения вероятностей:

Аналогично, для остальных гипотез:

Эта формула называется формулой Байеса. Вероятности гипотез называются апостериорными вероятностями, тогда как — априорными вероятностями.

Пример. Одного из трех стрелков вызывают на линию огня, он производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Формула Бернулли

При решении вероятностных задач часто бывает, что одно и тоже испытание повторяется многократно, и исход каждого испытания независит от исходов других. Такой эксперимент называют схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы. А вероятность появления события А в каждом случае постоянна и не изменяется от испытания к испытанию.

Биномиальное распределение — распределение числа успехов (появлений события).

Пример. Среди видео, которые снимает блогер, бывает в среднем 4% некачественных: то свет плохой, то звук пропал, то ракурс не самый удачный. Найдем вероятность того, что среди 30 видео два будут нестандартными.

Опыт заключается в проверке каждого из 30 видео на качество. Событие А — это какая-то неудача (свет, ракурс, звук), его вероятность p = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли можно найти ответ:

Ответ: вероятность плохого видео приблизительно 0,202. Блогер молодец🙂

Наивероятнейшее число успехов

Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:

Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.

Формула Пуассона

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. Например, 0.97 999 вычислить весьма затруднительно.

В этом случае для вычисления вероятности того, что в n испытаниях событие произойдет k раз, используют формулу Пуассона:

Здесь λ = np обозначает среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для p ≤ 0,1 и np ≤10.

События, для которых применима формула Пуассона, называют редкими, так как вероятность, что они произойдут — очень мала (обычно порядка 0,001-0,0001).

При больших np рекомендуют применять формулы Лапласа, которую рассмотрим чуть позже.

Пример. В айфоне 1000 разных элементов, которые работают независимо друг от друга. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.

P₁₀₀₀(3) = λ 3 /3! * e −λ = 2 3 /3! * e −2 ≈ 0,18.

Ответ: ориентировочно 0,18.

Теоремы Муавра-Лапласа

Кроме того, пусть P_n(k₁;k₂) — вероятность того, что число появлений события А находится между k₁ и k₂.

Локальная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Интегральная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Функции Гаусса и Лапласа обладают свойствами, которые пригодятся, чтобы правильно пользоваться таблицей значений этих функций:

Теоремы Лапласа дают удовлетворительное приближение при npq ≥ 9. Причем чем ближе значения q, p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность по сравнению с исходной формулой Бернулли.

Источник

Что такое достоверное событие

уМЕДХЕФ РПНОЙФШ, ЮФП НЩ ЪБОЙНБЕНУС НБФЕНБФЙЛПК Й ЙНЕЕН ДЕМП ОЕ У ТЕБМШОПУФША, Б МЙЫШ У ЕЈ НБФЕНБФЙЮЕУЛПК НПДЕМША. нЩ Й ВХДЕН ЙЪХЮБФШ ФПМШЛП НБФЕНБФЙЮЕУЛЙЕ НПДЕМЙ, Б РТЙМПЦЕОЙЕ ЙИ Л ТЕБМШОПУФЙ ПУФБЧЙН ОБ ДПМА НБФЕНБФЙЮЕУЛПК Й РТБЛФЙЮЕУЛПК УФБФЙУФЙЛЙ.

рТЙНЕТЩ УПВЩФЙК: — ЧЩРБМП ПДОП ЙМЙ ДЧБ ПЮЛБ; — ЧЩРБМП ОЕЮЈФОПЕ ЮЙУМП ПЮЛПЧ.

рТЙНЕТЩ УПВЩФЙК:
— РТЙ РЕТЧПН РПДВТБУЩЧБОЙЙ ЧЩРБМП ПДОП ПЮЛП;
— РТЙ ЧФПТПН РПДВТБУЩЧБОЙЙ ЧЩРБМП ПДОП ПЮЛП;
— ОБ ЛПУФСИ ЧЩРБМП ПДЙОБЛПЧПЕ ЮЙУМП ПЮЛПЧ;
— ОБ ПВЕЙИ ЛПУФСИ ЧЩРБМП ОЕЮЈФОПЕ ЮЙУМП ПЮЛПЧ.

фБЛ, ЬЛУРЕТЙНЕОФЩ ЙЪ РТЙНЕТПЧ 1, 2 Й 4 (ОП ОЕ 3) РТЙЧПДСФ Л ДЙУЛТЕФОЩН РТПУФТБОУФЧБН ЬМЕНЕОФБТОЩИ ЙУИПДПЧ.

2. еУМЙ Й ОЕУПЧНЕУФОЩ, ФП ;

еУМЙ УПВЩФЙЕ УПУФПЙФ ЙЪ ЬМЕНЕОФБТОЩИ ЙУИПДПЧ, ФП ЧЕТПСФОПУФШ ЬФПЗП УПВЩФЙС ТБЧОСЕФУС ПФОПЫЕОЙА :

ОБЪЩЧБЕНПК ЛМБУУЙЮЕУЛЙН ПРТЕДЕМЕОЙЕН ЧЕТПСФОПУФЙ.

нЩ ЧЙДЙН ФЕРЕТШ, ЮФП РПДУЮЈФ ЧЕТПСФОПУФЙ Ч ЛМБУУЙЮЕУЛПК УИЕНЕ УЧПДЙФУС Л РПДУЮЈФХ ПВЭЕЗП ЮЙУМБ «ЫБОУПЧ» Й ЮЙУМБ ЫБОУПЧ, ВМБЗПРТЙСФУФЧХАЭЙИ ЛБЛПНХ-МЙВП УПВЩФЙА. юЙУМП ЫБОУПЧ УЮЙФБАФ У РПНПЭША ЖПТНХМ ЛПНВЙОБФПТЙЛЙ.

еУМЙ РПТСДПЛ ОЕ ХЮЙФЩЧБФШ, ФП УМЕДХЕФ ПВЯСЧЙФШ ДЧБ РПУМЕДОЙИ ЙУИПДБ ПДОЙН Й ФЕН ЦЕ ТЕЪХМШФБФПН ЬЛУРЕТЙНЕОФБ, Й РПМХЮЙФШ ОЕ ЮЕФЩТЕ, Б ФТЙ ЙУИПДБ:

рЕТЧЩЕ ДЧБ ЙУИПДБ ЙНЕАФ ЧЕТПСФОПУФЙ РП 1/4, Б РПУМЕДОЙК — ЧЕТПСФОПУФШ 1/4+1/4=1/2.

тЕЪХМШФБФПН ЬЛУРЕТЙНЕОФБ СЧМСЕФУС ОБВПТ ЙЪ ЫБТПЧ. нПЦОП ОЕ ХЮЙФЩЧБФШ ЙМЙ ХЮЙФЩЧБФШ РПТСДПЛ УМЕДПЧБОЙС ЫБТПЧ, ЧЕТПСФОПУФШ ОЕ ДПМЦОБ ЪБЧЙУЕФШ ПФ УРПУПВБ РПДУЮЈФБ.

чЩВПТ У ХЮЈФПН РПТСДЛБ. пВЭЕЕ ЮЙУМП ЬМЕНЕОФБТОЩИ ЙУИПДПЧ ЕУФШ ЮЙУМП УРПУПВПЧ ТБЪНЕУФЙФШ ЬМЕНЕОФПЧ ОБ НЕУФБИ: РП ФЕПТЕНЕ 2,

Источник

Достоверное, недостоверное, случайные и несовместимые события

1. Достоверное, недостоверное, случайные и несовместимые события.

Достоверным называют событие, которое обязательно произойдёт, если будет осуществлена определенная совокупность условий.

Недостоверное или невозможное событие, которое заведомо не произойдёт, если будет осуществлена совокупность событий.

Случайное событие при осуществлении совокупности событий может либо произойти, либо не произойти.

События называют несовместными, если появление одного из них исключает появление двух других событий в одном и том же испытании

2. Классическое определение вероятности.

3. Элементарные исходы.

В формулах обозначается буквой n. Исходы = испытания.

Комбинации, состоящие из одних и тех же «n» различных элементов и отличающиеся порядком их расположения. Число всех возможных перестановок

Это комбинации из «n» различных элементов, которые отличаются либо составом элементов, либо их порядком.

Это комбинации, составленные из “n” различных элементов по “m” элементов, которые отличаются хотя бы одним элементом.

7. Относительная частота.

Это отношение числа испытаний, в которых событие появилось, к общему числу фактически произведённых испытаний.

m – число появления события, n – общее число испытаний.

8. Полная группа событий. Равновозможные события.

Сумма вероятностей A1,A2,…,An, образуют полную группу

9. Противоположные события.

Это два единственно возможных события образующих полную группу

10. Сумма двух событий.

Суммой A+B двух событий A и B называют событие, состоящее в появление события A, или события B, или обоих этих событий.

11. Сумма нескольких событий.

Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.

Например, событие A+B+C состоит в появлении одного из следующих событий: А;B;С;A и B,A и C;B и C;A и B и С.

12. Произведение двух событий.

Произведением двух событий A и B называют событие AB, состоящее в совместном появлении этих событий.

13. Произведение нескольких событий.

Произведением нескольких событий называют событие, состоящее в совместном появлении этих

14. Испытания независимые относительно одного события.

Пусть вероятность события B не зависит от появления события A.

Событие B называют независимым от события A, если появление события A не изменят вероятности события B, то есть если условная вероятность события B равна его безусловной вероятности:

Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противоположном случае события называют зависимыми

15. Теорема умножения событий.

Для независимых событий теорема умножения P(АВ) = P(А)*PA(B) имеет вид P(AB) = P(A)*Р(B), т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

16. Условная вероятность.

Условной вероятностью называют вероятность события B, вычисленную в предположении, что событие A уже наступило.

17. Вероятность совместного появления двух событий.

Теорема Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого вычисленную в предположении, что первое событие уже наступило:

18. Вероятность появления хотя бы одного события.

Вероятность появления хотя бы одного из событий A1,A2,…,An, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий

Это совмещение нескольких отдельных событий, которые называются простыми

Простое событие – это результат испытания

20. Дискретная случайная величина.

Случайной называю величину, которая в результате испытания примет одно и только одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Случайная величина называется дискретной, если она может принимать только конечное или счётное множество возможных значений. Дискретные случайные величины, которые могут принимать лишь целые неотрицательные значения, называются целочисленными и возникают при каких-то подсчётах.

21. Непрерывная случайная величина.

Случайная величина называется непрерывной, если она может принимать любое значение из некоторого интервала, причём этот интервал может быть ограниченным или неограниченным. Непрерывная случайная величина имеет несчётное множество значений, которые сплошь заполняют некоторый интервал числовой оси или всю ось. Возникает при изменении отклонения контрольного параметра изделия массового производства от её номинального значения, при изменении расстояния от центра цели до точки падения снаряда.

22. Закон распределения дискретной случайной величины.

Называют соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

23. Биноминальное распределение.

Биноминальным распределением вероятностей называется распределение вероятностей, определяемое формулой Бернулли.

— эта формула называется биноминальной так как её правая часть представляет собой (m+1) бином Ньютона:

Вероятность того, что событие A в n испытаниях наступило k раз.

Если в каждом из n независимых испытаний вероятность p появления события A постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний велико.

Пусть событие A может наступить при условии появления одного из несовместных событий B1, B2, …, Bn, образующих полную группу. Поскольку заранее не известно, какое событие наступит, их называют гипотезами.

Поток – это последовательность однородных событий, следующих одно за другим в случайные моменты времени (например, поток отказов технических систем, поток сообщений, поступающих в АСУ, и тому подобные).

Наиболее важными свойствами потоков являются : стационарность, ординарность и отсутствие последействия.

28. Свойства потоков события.

Стационарность потока означает, что его вероятностные характеристики не зависят от времени. Важнейшей характеристикой потока является его интенсивность l – среднее число событий в единице времени. Для стационарного потока l=const, а для нестационарного l=l(t) – функция времени.

Ординарность потока означает практическую невозможность появления двух и более событий в один и тот же момент времени.

Отсутствие последействия означает, что события появляются в потоке независимо друг от друга, т. е. вероятность появления определенного числа событий за некоторый произвольно выбранный промежуток времени не зависит от того, сколько событий произошло раньше (не зависит от предыстории изучаемого потока).

29. Независимые события. Интенсивность потока.

Интенсивность потока — среднее число событий, которые появляются в единицу времени.

30. Простейший (Пуассоновский) поток событий.

(2.2)

где а – среднее число событий, приходящихся на участок t. Для простейшего потока а=lt, а для нестационарного пуассоновского .

31. Закон распределения Пуассона.

Вероятность того, что в n испытаниях, в каждом из которых вероятность появления события мала и равна p , событие наступит ровно k раз (безразлично в какой последовательности)) приближенно равна (тем точнее, чем больше n).

, где — среднее число появлений события в n испытаниях. В этом случае говорят, что случайная величина распределена по закону Пуассона.

32. Геометрическое распределение.

Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель p=0,7. Найти вероятность того что попадание произойдёт при третьем выстреле.

Решение: Так как k=3, p=0,7, то q=0,3; искомая вероятность

33. Функция распределения.

Называют функцию F(x), определяющую для каждого x вероятность того, что случайная величина X примет значение меньшее x, то есть F(x)=P(X 0, ограничена снизу величиной 1–D(X)/ε2, т. е.

Таким образом, гамма-распределение является двухпараметрическим распределением, оно занимает важное место в математической статистике и теории надёжности. Это распределение имеет ограничение с одной стороны

60. Распределение Эрланага k-го порядка.

(x>0;k=1,2,3…)

61. Функция надёжности.

Функцией надёжности R(t) называют функцию, определяющую вероятность безотказной работы элемента за время t: R(t)=P(T>t)=1-F(t)

Показательным законом надёжности называют функцию надёжности определяемую равенством где — интенсивность отказов.

62. Система двух случайных величин.

Совокупность двух случайных величин (X,Y), рассматриваемых совместно, называется системой двух случайных величин, геометрически интерпретируется как случайная точка с координатами (X,Y) на плоскости xOy или как случайный вектор, направленный из начала координат.

Величины, возможные значения которых определяются двумя, тремя, …, n числами, называют соответственно двумерными, трехмерными, … n-мерными.

63. Закон распределения вероятностей дискретной двумерной случайной величины.

Называют перечень возможных значений этой величины, то есть пар чисел x­i,yj и их вероятностей p(xi,yi)(i=1,2,…,n; j=1,2,…m). Обычно закон распределения задают в виде таблицы СС двойным входом.

Первая строка таблицы содержит все возможные значении составляющей X, а первый столбец – все возможные составляющей Y. В клетке, стоящей на пересечении «столбца xi» и «строки yi», указана вероятность p(xi,yi) того, что двумерная случайная величина примет значение (xi­,yi)

Называют функцию F(x,y), определяющую для каждой пары чисел x,y вероятность того, что X примет значение, меньшее x, и при этом, Y примет значение, меньшее y: F(x,y)=P(X 0, ограничена снизу величиной 1–D(X)/ε2, т. е.

Таким образом, гамма-распределение является двухпараметрическим распределением, оно занимает важное место в математической статистике и теории надёжности. Это распределение имеет ограничение с одной стороны

(x>0;k=1,2,3…)

61. Функция надёжности.

Показательным законом надёжности называют функцию надёжности определяемую равенством где — интенсивность отказов.

62. Система двух случайных величин.

Совокупность двух случайных величин (X,Y), рассматриваемых совместно, называется системой двух случайных величин, геометрически интерпретируется как случайная точка с координатами (X,Y) на плоскости xOy или как случайный вектор, направленный из начала координат.

Величины, возможные значения которых определяются двумя, тремя, …, n числами, называют соответственно двумерными, трехмерными, … n-мерными.

63. Закон распределения вероятностей дискретной двумерной случайной величины.

Называют перечень возможных значений этой величины, то есть пар чисел x­i,yj и их вероятностей p(xi,yi)(i=1,2,…,n; j=1,2,…m). Обычно закон распределения задают в виде таблицы СС двойным входом.

Первая строка таблицы содержит все возможные значении составляющей X, а первый столбец – все возможные составляющей Y. В клетке, стоящей на пересечении «столбца xi» и «строки yi», указана вероятность p(xi,yi) того, что двумерная случайная величина примет значение (xi­,yi)

Называют функцию F(x,y), определяющую для каждой пары чисел x,y вероятность того, что X примет значение, меньшее x, и при этом, Y примет значение, меньшее y: F(x,y)=P(X

Источник