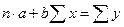Что такое достоверность аппроксимации
Метод аппроксимации в Microsoft Excel
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Выполнение аппроксимации
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
Рассмотрим каждый из вариантов более подробно в отдельности.
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
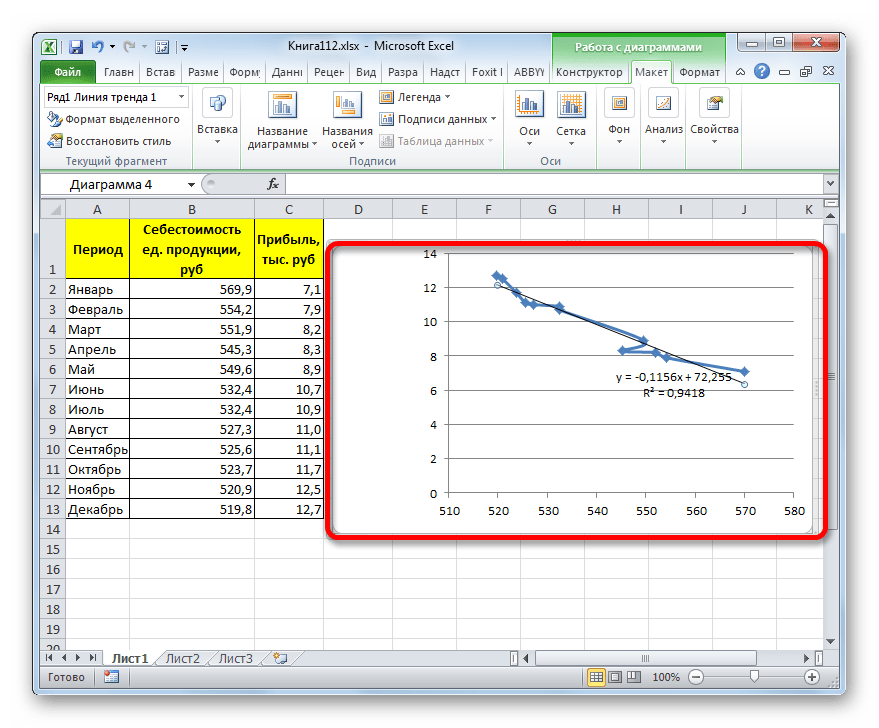
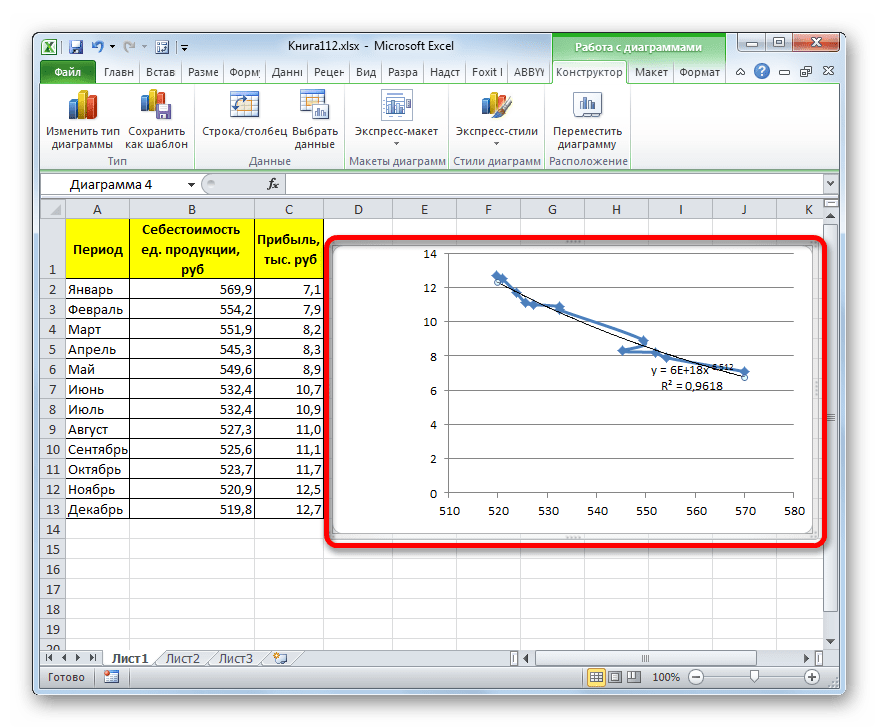
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
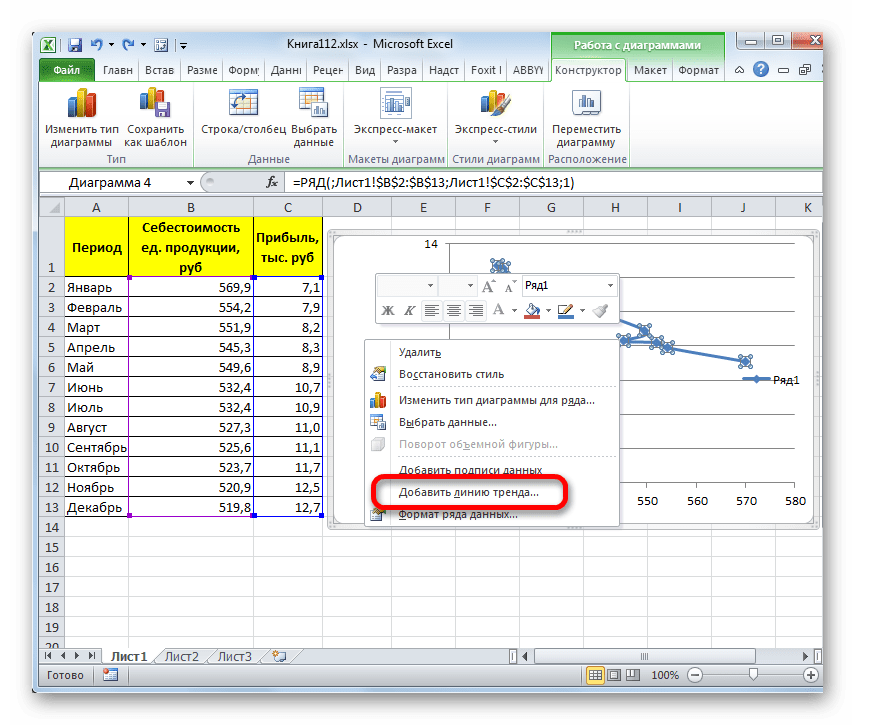
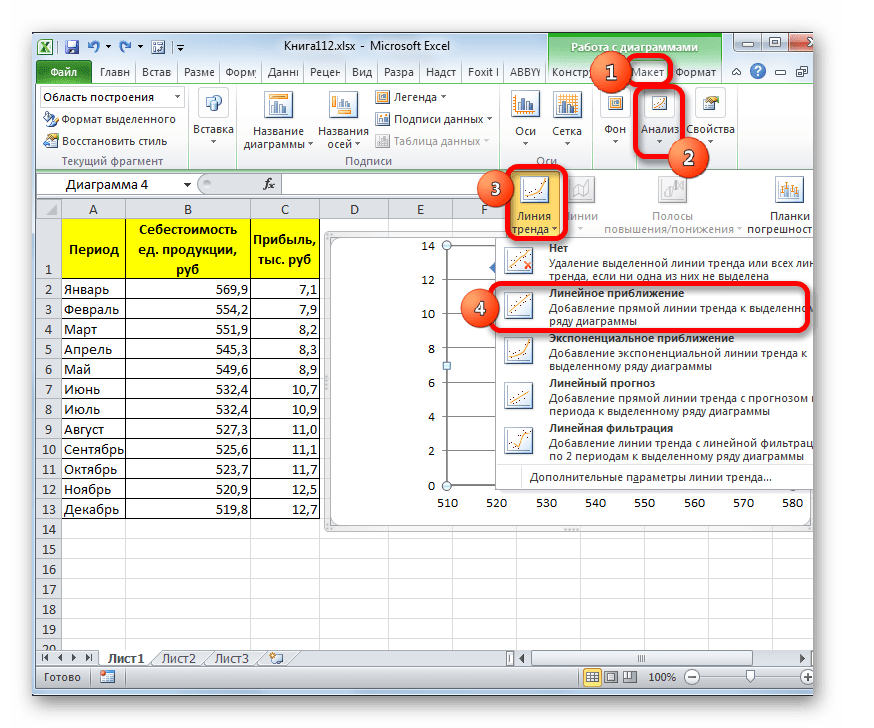
Существует ещё один вариант её добавления. В дополнительной группе вкладок на ленте «Работа с диаграммами» перемещаемся во вкладку «Макет». Далее в блоке инструментов «Анализ» щелкаем по кнопке «Линия тренда». Открывается список. Так как нам нужно применить линейную аппроксимацию, то из представленных позиций выбираем «Линейное приближение».
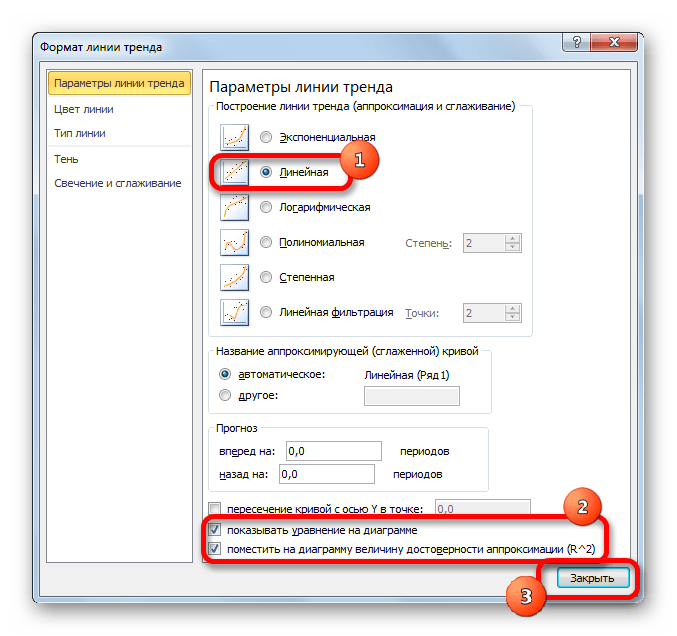
В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
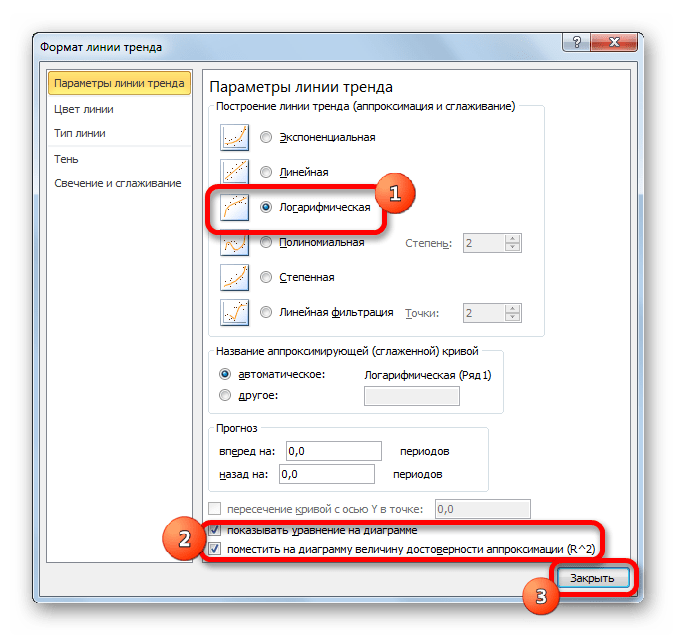
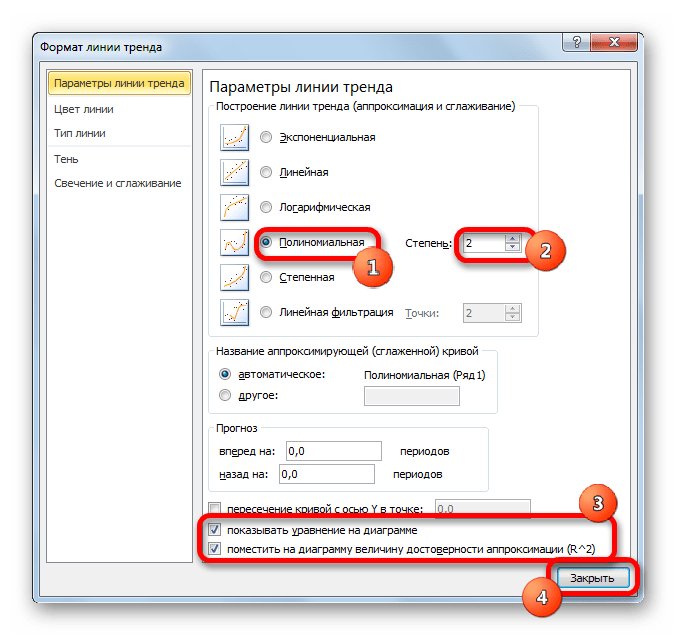
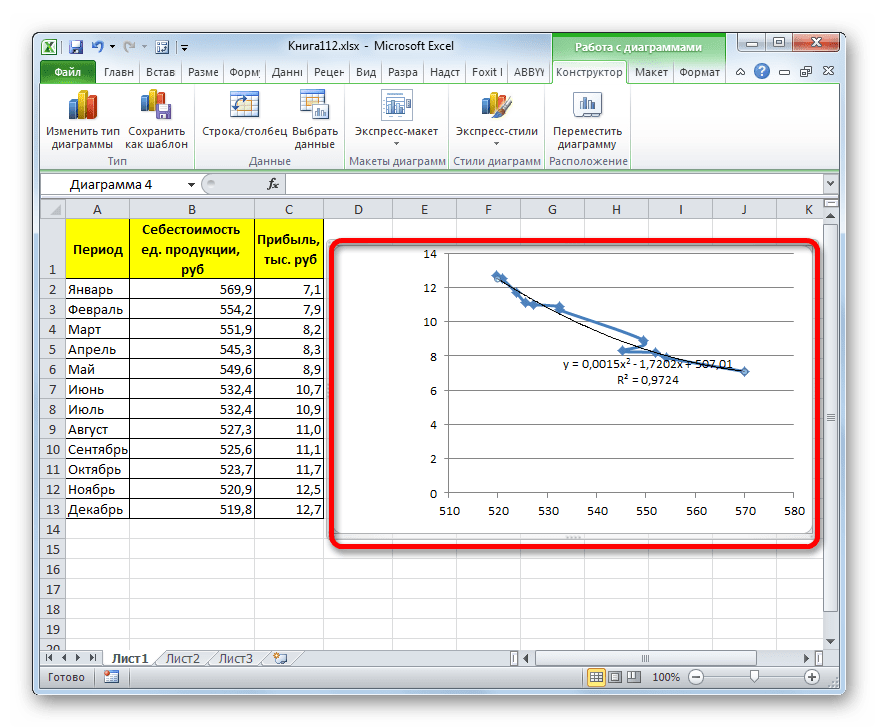
При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.
Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.
После того, как провели все вышеуказанные настройки. Жмем на кнопку «Закрыть», размещенную в нижней части окна.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
В конкретно нашем случае формула принимает такой вид:
Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
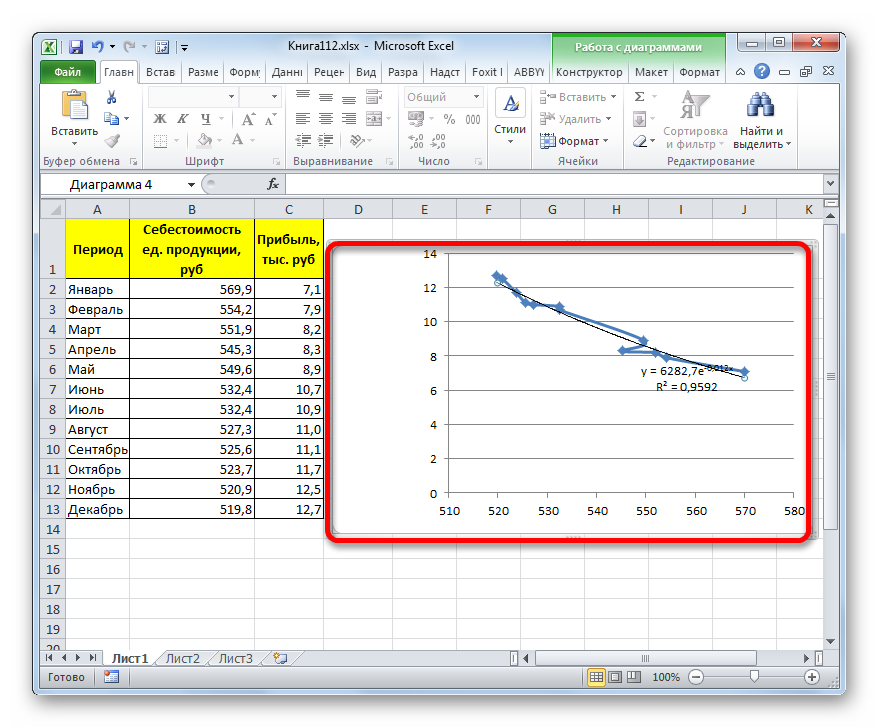
Способ 2: экспоненциальная аппроксимация
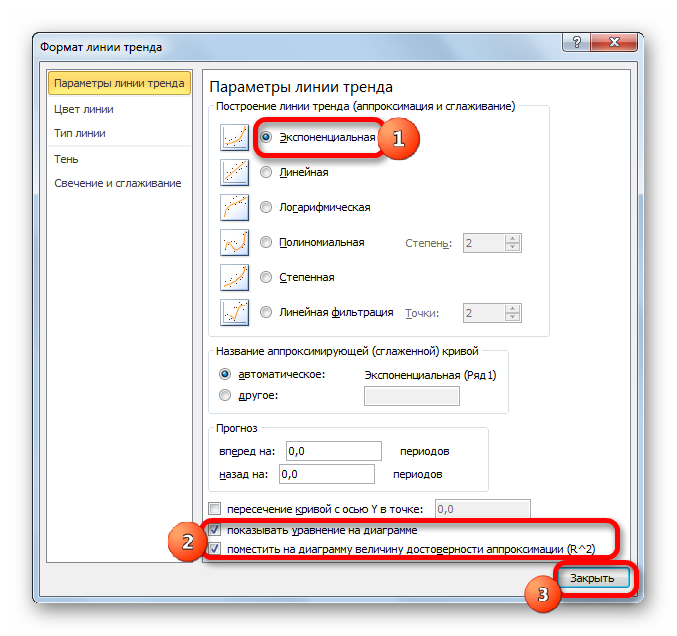
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
Общий вид функции сглаживания при этом такой:
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
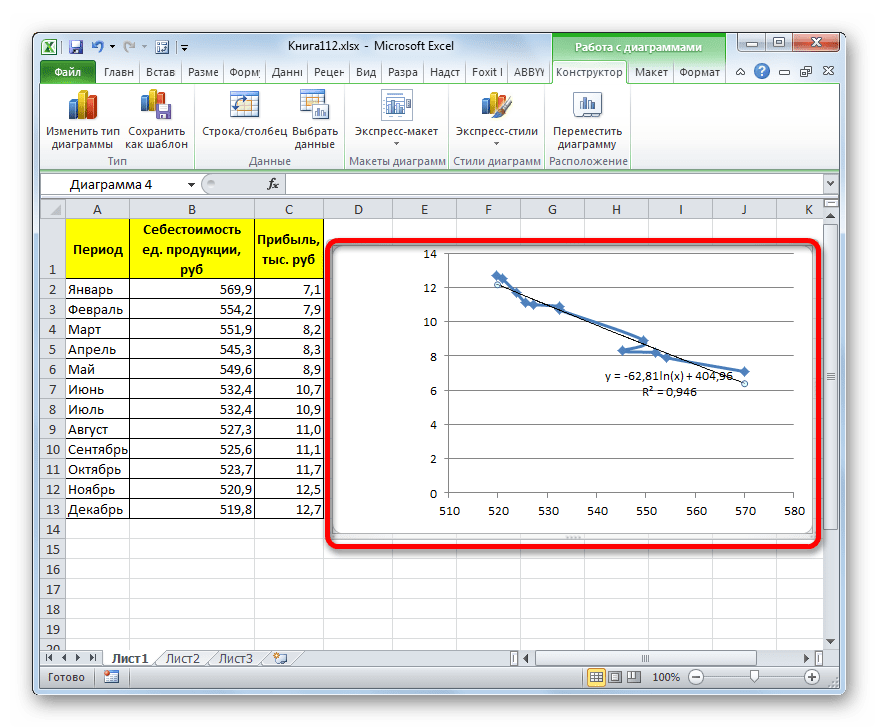
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
В общем виде формула сглаживания выглядит так:
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
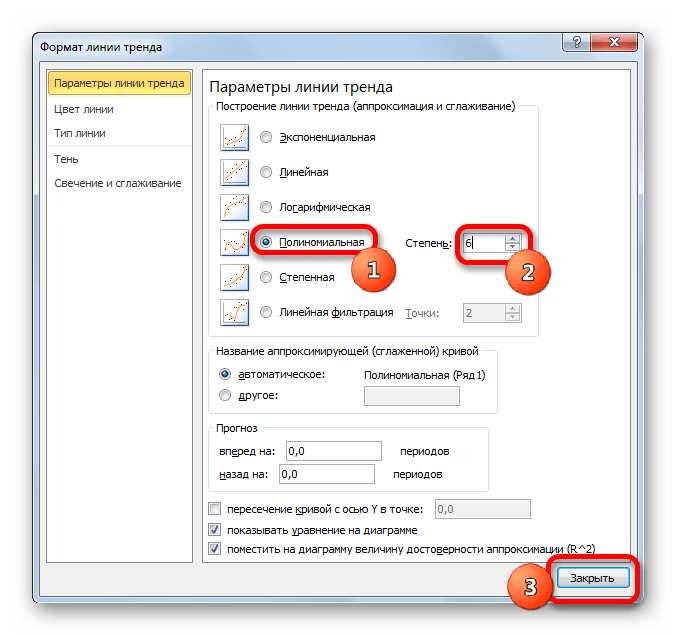
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
Данный метод наиболее успешно можно применять в том случае, если данные носят постоянно изменчивый характер. Функция, описывающая данный вид сглаживания, выглядит таким образом:
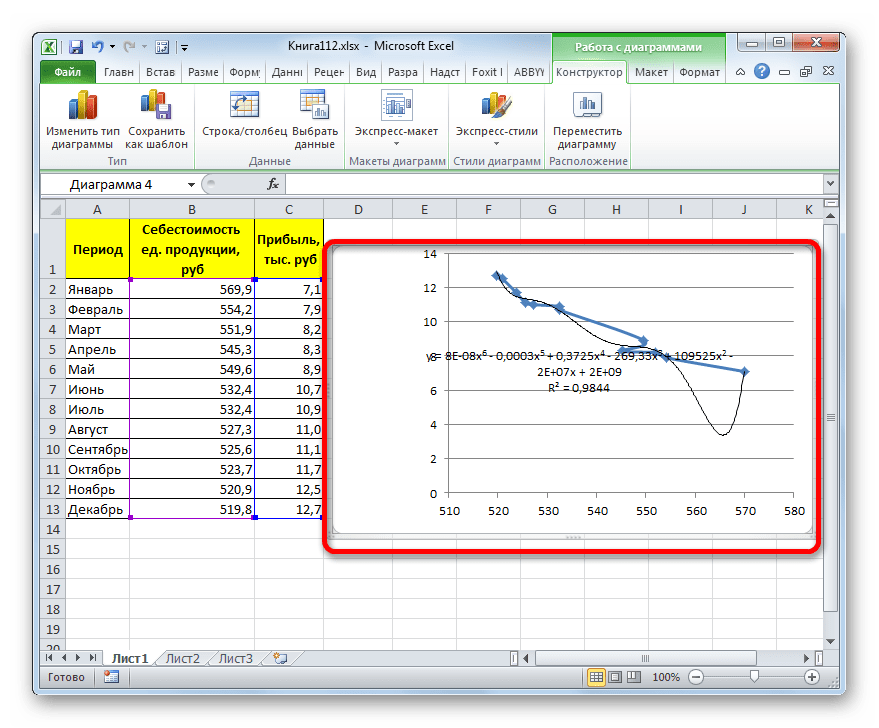
В нашем случае формула приняла такой вид:
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
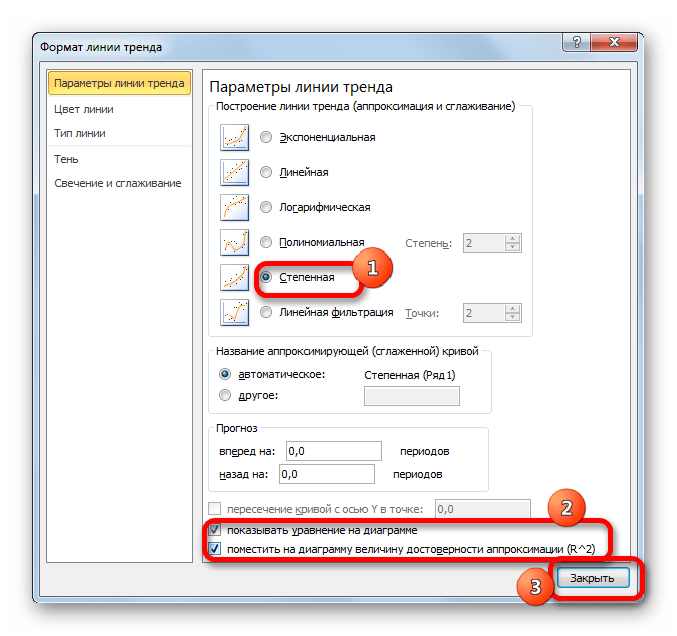
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
В конкретно нашем случае она выглядит так:
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Помимо этой статьи, на сайте еще 12554 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Корреляция и регрессия
Когда вы исследуете закономерности в своих данных, как вы можете определить, насколько тесно связаны между собой две переменные? Можете ли вы использовать одну переменную для предсказания другой?
В этом модуле вы познакомитесь с концепциями корреляции и регрессии, которые могут помочь вам в дальнейшем изучении, понимании и обмене данными.
Цели
По завершении этого модуля вы сможете:
Раздел 1. Корреляция
В этом модуле вы познакомитесь с двумя концепциями, которые помогут вам в изучении взаимосвязей между переменными: корреляция и регрессия. Начнем с корреляции.
Что такое корреляция?
Корреляция – это техника, которая может показать, насколько сильно связаны пары количественных переменных. Например, количество ежедневно потребляемых калорий и масса тела взаимосвязаны, но эта связь не абсолютная.
Многие из нас знают кого-то, кто очень худой, несмотря на то, что он/она регулярно потребляет большое количество калорий, и мы также знаем кого-то, у кого есть проблемы с лишним весом, даже когда он/она сидит на диете с пониженным содержанием калорий.
Однако средний вес людей, потребляющих 2000 калорий в день, будет меньшим, чем средний вес людей, потребляющих 2500, а их средний вес будет еще меньше, чем у людей, потребляющих 3000, и так далее.
Корреляция может сказать вам, насколько тесно разница в весе людей связана с количеством потребляемых калорий.
Корреляция между весом и потреблением калорий – это простой пример, но иногда данные, с которыми вы работаете, могут содержать корреляции, которых вы никак не ожидаете. А иногда вы можете подозревать корреляции, не зная, какие из них самые сильные. Корреляционный анализ помогает лучше понять связи в ваших данных.
Диаграммы разброса или Точечные диаграммы используются для графического представления взаимосвязей между количественными показателями. Диаграмма показывает данные и позволяет нам проверить свои предположения, прежде чем устанавливать корреляции. Глядя на взаимосвязь между продажами и маркетингом, можно предположить наличие в них корреляции. По мере того, как одна переменная растет, другая, похоже, тоже увеличивается.
Диаграмма, указывающая на корреляцию между двумя количественными переменными
Корреляция против причинно-следственной связи
Теперь вы знаете, как определяется корреляция и как ее можно представить графически. Теперь давайте посмотрим, как понимать корреляцию.
Во-первых, важно понимать, что корреляция никогда не доказывает наличие причинно-следственной связи.
Корреляция говорит нам только о том, насколько сильно пара количественных переменных линейно связана. Она не объясняет, как и почему.
Например, продажи кондиционеров коррелируют с продажами солнцезащитных кремов. Люди покупают кондиционеры, потому что они купили солнцезащитный крем, или наоборот? Нет. Причина обеих покупок явно в чем-то другом, в данном случае – в жаркой погоде.
Измерение корреляции
Корреляция Пирсона, также называемая коэффициентом корреляции, используется для измерения силы и направления (положительного или отрицательного) линейной связи между двумя количественными переменными. Когда корреляция измеряется в выборке данных, используется буква r. Критерий Пирсона r может находиться в диапазоне от –1 до 1.
Когда r = 1, существует идеальная положительная линейная связь между переменными, это означает, что обе переменные идеально коррелируют с увеличением значений. Когда r = –1, существует идеальная отрицательная линейная связь между переменными, это означает, что обе переменные идеально коррелируют при уменьшении значений. Когда r = 0, линейная связь между переменными не наблюдается.
На графиках разброса ниже показаны корреляции, где r = 1, r = –1 и r = 0.
Переверните каждую карту ниже, чтобы увидеть значение для этой совокупности.
Идеальная положительная корреляция
Когда r = 1, есть идеальная положительная линейная связь между переменными, и это означает, что обе переменные идеально коррелируют с увеличением значений.
Идеальная отрицательная корреляция
Когда r = –1, существует идеальная отрицательная линейная связь между переменными, и это означает, что обе переменные идеально коррелируют при уменьшении значений.
Нет линейной корреляции
Когда r = 0, линейная зависимость между переменными не наблюдается.
С реальными данными вы никогда не увидите значений r «–1», «0» или «1».
Как правило, чем ближе r к 1 или –1, тем сильнее корреляция, это показано в следующей таблице.
Сила корреляции
Очень сильная корреляция
Очень слабая корреляция или ее нет вообще
Условие корреляции
Чтобы корреляции были значимыми, они должны использовать количественные переменные, и описывать линейные отношения, при этом не может быть выбросов.
В 1973 году статистик по имени Фрэнсис Анскомб разработал показатель «квартет Анскомба», он показывает важность визуального представления данных в виде графиков, а не простого выполнения статистических тестов.
Выделенный график разброса в верхнем левом углу – единственный, который удовлетворяет условиям корреляции.
Четыре визуализации в его квартете показывают одну и ту же линию тренда, поэтому значение r будет одинаковым для всех четырех.
Что вы заметили? Только один из графиков рассеяния соответствует критериям линейности и отсутствия выбросов.
Другими словами, мы не должны проводить корреляции на трех из четырех примерах, потому что не имеет смысла устанавливать сильные отношения.
Проверка знаний
Силу корреляции при значении r, равному –0,52, лучше всего можно описать как:
Резюме
Итак, вы ознакомились с концепциями статистической техники корреляции. На следующем уроке вы узнаете о линейной регрессии.
Раздел 2. Линейная регрессия
На предыдущем уроке вы узнали, что корреляция относится к направлению (положительному или отрицательному) и силе связи (от очень сильной до очень слабой) между двумя количественными переменными.
Линейная регрессия также показывает направление и силу взаимосвязи между двумя числовыми переменными, но регрессия использует наиболее подходящую прямую линию, проходящую через точки на диаграмме рассеяния, чтобы предсказать, как X вызывает изменение Y. При корреляции значения X и Y взаимозаменяемы. При регрессии результаты анализа изменятся, если поменять местами X и Y.
Диаграмма рассеяния с линией регрессии
Линия регрессии
Как и в случае с корреляциями, для того, чтобы регрессии были значимыми, они должны:
Как и корреляция, линейная регрессия отображается на диаграмме рассеяния
Линия регрессии на диаграмме рассеяния – это наиболее подходящая прямая линия, которая проходит через точки на диаграмме рассеяния. Другими словами, это линия, которая проходит через точки с наименьшим расстоянием от каждой из них до линии (поэтому в некоторых учебниках вы можете встретить название «регрессия наименьших квадратов»).
Почему эта линия так полезна? Мы можем использовать вычисление линейной регрессии для вычисления или прогнозирования нашего значения Y, если у нас есть известное значение X.
Чтобы было понятнее, давайте рассмотрим пример.
Пример регрессии
Представьте, что вы хотите предсказать, сколько вам нужно будет заплатить, чтобы купить дом площадью 1,500 квадратных футов.
Давайте используем для этого линейную регрессию.
Вот диаграмма рассеяния, показывающая цены на жилье (ось Y) и площадь в квадратных футах (ось x).
Вы можете видеть, что дома с большим количеством квадратных футов, как правило, стоят дороже, но сколько именно вам придется потратить на дом размером 1500 квадратных футов?
Диаграмма рассеяния цен на дома и квадратных метров
Чтобы помочь вам ответить на этот вопрос, проведите линию через точки. Это и будет линия регрессии. Линия регрессии поможет вам предсказать, сколько будет стоить типовой дом определенной площади в квадратных метрах. В этом примере вы можете видеть уравнение для линии регрессии.
Уравнение линии регрессии
Уравнение линии регрессии: Y = 113x + 98,653 (с округлением).
Что означает это уравнение? Если вы купили просто место без площади (пустой участок), цена составит 98,653 доллара. Вот как можно решить это уравнение:
Чтобы найти Y, умножьте значение X на 113, а затем добавьте 98,653. В этом случае мы не смотрим на квадратные метры, поэтому значение X равно «0».
Значение 98,653 называется точкой пересечения по оси Y, потому что здесь линия пересекает ось Y. Это – значение Y, когда X равно «0».
Но что такое 113? Число «113» – это наклон линии. Наклон – это число, которое описывает как направление, так и крутизну линии. В этом случае наклон говорит нам, что за каждый квадратный фут цена дома будет расти на 113 долларов.
Итак, сколько вам нужно будет потратить на дом площадью 1500 квадратных футов?
Взгляните еще раз на эту диаграмму рассеяния. Синие отметки – это фактические данные. Вы можете видеть, что у вас есть данные для домов площадью от 1100 до 2450 квадратных футов.
Насколько можно быть уверенным в результате, используя приведенное выше уравнение, чтобы спрогнозировать цену дома площадью в 500 квадратных футов? Насколько можно быть уверенным в результате, используя приведенное выше уравнение, чтобы предсказать цену дома площадью 10,000 квадратных футов?
Поскольку оба этих измерения находятся за пределами диапазона фактических данных, вам следует быть осторожными при прогнозировании этих значений.
Величина достоверности аппроксимации
Наведите курсор на линию регрессии, чтобы увидеть значение величины достоверности аппроксимации r.
В дополнение к уравнению в этом примере мы также видим значение величины достоверности аппроксимации r (также известная как коэффициент детерминации).
Это значение является статистической мерой того, насколько близки данные к линии регрессии или насколько хорошо модель соответствует вашим наблюдениям. Если данные находятся точно на линии, значение величины достоверности аппроксимации будет 1 или 100%, и это означает, что ваша модель идеально подходит (все наблюдаемые точки данных находятся на линии).
Для наших данных о ценах на жилье значение величины достоверности аппроксимации составляет 0,70, или 70%.
Корреляция против причинно-следственной связи
Теперь давайте рассмотрим, как отличить линейную регрессию от корреляции.
Линейная регрессия
Корреляция
Готовы проверить свои знания? В следующем упражнении определите, чему соответствует каждое из описаний: корреляции или регрессии.
Варианты для категорий: «корреляция» или «регрессия».
Измеряется величиной достоверности аппроксимации
Прогнозирует значения Y на основе значений X.
Не предсказывает значения Y из значений X, только показывает взаимосвязь.
Переменные оси X и Y взаимозаменяемы.
Если поменять местами X и Y, результаты анализа изменятся.
Резюме
Итак, здесь вы познакомились со статистическими концепциями корреляции и регрессии. Это поможет вам лучше исследовать и понимать данные, с которыми вы работаете, путем изучения взаимосвязей в них.
Коэффициент детерминации или аппроксимации (RI или R2).
Квадрат коэффициента корреляции (r 2 ) называется коэффициентом детерминации или аппроксимации и обозначается RI или R 2 .Этот коэффициент показывает долю (%) тех изменений, которые в данном явлении зависят от изучаемого фактора. Коэффициент детерминации является более непосредственным и прямым способом выражения зависимости одной величины от другой, и в этом отношении он предпочтительнее коэффициента корреляции. В случаях, где известно, что независимая переменная у находится в причинной связи с независимой переменной х, значение r 2 показывает ту долю элементов в вариации у, которая определена влиянием х. Так, например, если было установлено, что коэффициент корреляции между дозой азотного удобрений и содержанием белка в зерне составил 0,96, то можно утверждать, что 92% (0,96 · 0,96) колебаний содержания белка в зерне обусловлено варьированием доз азотного удобрения.
В практической статистике, коэффициенты детерминации или аппроксимации более широко используются при характеристике изучаемых взаимосвязей. Его можно использовать не только для описания прямолинейной связи между признаками, но и криволинейной (в этом случае, его называют коэффициент аппроксимации, и он представляет собой квадрат корреляционного отношения 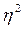
Обычно при определении взаимосвязи между изучаемыми признаками устанавливают последовательно коэффициент корреляции, коэффициент детерминации (или аппроксимации) и скорректированный коэффициент детерминации (RIadj), который рассчитывается по формуле:
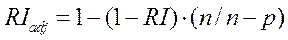
Именно, скорректированный коэффициент детерминации позволяет судить с высокой степенью вероятности о том, насколько процентов варьирование результативного признака обусловлено варьированием факториального.
Множественная корреляция.Корреляцияназывается множественной если на величину результативного признака одновременно влияют несколько факториальных.
Частные коэффициенты корреляции рассчитываются по формулам:
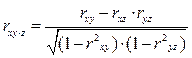
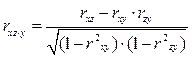
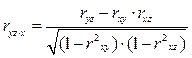
Ошибку и критерий значимости частной корреляции определяют аналогично, что и парной корреляции.
Множественный коэффициент корреляции нескольких переменных – это показатель тесноты связи между одним из признаков (буква индекса перед точкой) и совокупностью других признаков (буквы индекса после точки). Коэффициент корреляции трёх переменных рассчитывается по следующим формулам:
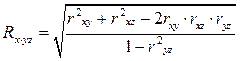
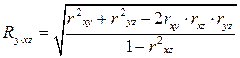
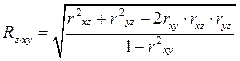
Эти формулы позволяют легко вычислить множественные коэффициенты корреляции при известных значениях коэффициентов парной корреляции. Коэффициент R положителен и всегда находится в пределах от 0 до 1.
Квадрат коэффициента множественной корреляции называется коэффициентом множественной детерминации, который, как и обыкновенный коэффициент детерминации, обозначается RI или R 2 .
Значимость множественной корреляции оценивается по F – критерию:
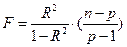
где n – объём выборки,
p – число независимых переменных или признаков.
Теоретическое значение F – критерия берут из приложения III для df1 = р-1 и df2 = n–p степеней свободы и принятого уровня значимости. Нулевая гипотеза о равенстве множественного коэффициента корреляции в совокупности нулю (Н0 : R = 0) принимается, если Fфакт
Регрессионный анализ заключается в том, чтобы отыскать линию (прямую в случае линейной корреляции, параболу первого, второго и т.д. порядка при криволинейной зависимости) наиболее точно выражающую зависимость одного признака от другого. Кроме того, при помощи регрессионного анализа можно выяснить ошибку опытных данных, влияющих на конечные результаты исследования.
Существует множество аналитических методов определения регрессии, которые зависят от типа регрессии (парная или множественная), а также от типа, по которому отмечается взаимосвязь (прямая линия, гипербола, парабола и т.д.).
Парная регрессияхарактеризует связь между двумя признаками: результативным и факторным. Аналитически связь между ними описывается уравнениями:
прямой 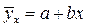
гиперболы
параболы 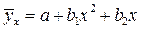
Определить тип уравнения можно, исследуя зависимость графически, однако в практике не часто прибегают к этому методу определения уравнения.
Оценка параметров уравнений регрессии (а, b1, b2…) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметров модели при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
SS = 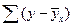
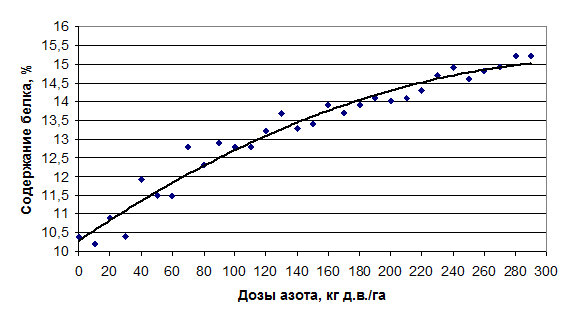
Рисунок 8. Прямая линия регрессии на графике зависимости содержания белка в зерне ячменя от дозы азотного удобрения
Рисунок 9. Параболическая линия регрессии на графике зависимости содержания белка в зерне ячменя от дозы азотного удобрения
В отношении установленной зависимости между дозами азотного удобрения и содержания белка в зерне ячменя данное правило можно интерпретировать так: прямая линия должна быть максимально приближена ко всем значениям ху или ух, что отчётливо отмечается на графике (рисунок 2 и рисунок 3)
Задача регрессионного анализа состоит в том, чтобы установить параметры уравнения регрессии (а, b1, b2…) или иными словами, описать взаимосвязь между изучаемыми показателями с помощью уравнения, оценить на какую величину изменяется значение результативного признака, при изменении факторного на единицу.
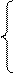
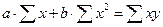
где n – объём исследуемой совокупности (число единиц наблюдений).
В уравнениях регрессии параметр a показывает усреднённое влияние на результативный признак неучтённых в уравнении факторных признаков: коэффициент регрессии b показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения. Таким образом, решая данную систему нормальных уравнений задача состоит именно в определении параметров уравнения регрессии a и b.
Уравнение линейной регрессии 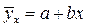
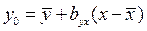
или аналогично для нахождения теоретической линии регрессии х по у: 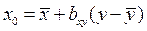
где 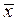
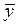
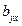
Коэффициенты регрессии вычисляются по формулам:
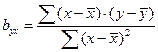
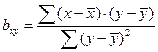
Числители этих формул представляют собой сумму произведений отклонений значений х и у от своих средних (то есть числитель формулы (64) расчёта коэффициента корреляции), а знаменатели – сумму квадратов отклонений от средних. Таким образом, связь между коэффициентов корреляции и коэффициентом регрессии можно математически выразить так:
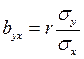
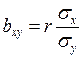
Произведение коэффициентов регрессии равно коэффициенту детерминации:
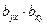
При регрессионном анализе проводят обычно две оценки выборочных коэффициентов регрессии: а) оценки величины отклонений от линии регрессии и б) оценку существенности b, то есть значимость отклонения его от нуля.
Ошибка коэффициента регрессии вычисляется по формуле:
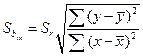

Критерий существенности коэффициента регрессии определяют по формуле:
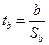
Существенность коэффициента регрессии оценивают по приложению II, число степеней свободы df принимают равным n–2.
ПРИЛОЖЕНИЯ
Значения критерия ω (по Н.Ф. Деревицкому)
| Число степеней свободы | Уровень значимости | Число степеней свободы 5%-ный | Уровень значимости |
| 5%-ный | 1%-ный | 5%-ный | 1%-ный |
| 1,41 | 1,41 | 1,93 | 2,45 |
| 1,64 | 1,72 | 1,93 | 2,45 |
| 1,76 | 1,92 | 1,93 | 2,46 |
| 1,81 | 2,05 | 1,93 | 2,46 |
| 1,85 | 2,14 | 1,94 | 2,47 |
| 1,87 | 2,21 | 1,94 | 4,47 |
| 1,88 | 2,26 | 1,94 | 2,48 |
| 1,90 | 2,29 | 1,94 | 2,48 |
| 1,90 | 2,32 | 1,94 | 2,49 |
| 1,91 | 2,34 | 1,94 | 2,49 |
| 1,92 | 2,35 | 1,94 | 2,50 |
| 1,92 | 2,38 | 1,94 | 2,50 |
| 1,92 | 2,39 | 1,94 | 2,50 |
| 1,92 | 2,41 | 1,94 | 2,51 |
| 1,93 | 2,42 | 1,95 | 2,53 |
| 1,93 | 2,43 | 1,95 | 2,54 |
| 1,93 | 2,44 | 1,96 | 2,55 |
 | 1,96 | 2,58 |
Стандартные значения критерия t (критерия Стьюдента) на 5%-ном, 1%-ном и 0,1%-ном уровне значимости (округлены до десятых)
| Число степеней свободы | Уровень значимости | Число степеней свободы | Уровень значимости | |||
| 0,05 | 0,01 | 0,001 | 0,05 | 0,01 | 0,001 | |
| 12,7 | 63,7 | 637,0 | 2,2 | 3,0 | 4,1 | |
| 4,3 | 9,9 | 31,6 | 14-15 | 2,1 | 3,0 | 4,1 |
| 3,2 | 5,8 | 12,9 | 16-17 | 2,1 | 2,9 | 4,0 |
| 2,8 | 4,6 | 8,6 | 18-20 | 2,1 | 2,9 | 3,9 |
| 2,6 | 4,0 | 6,9 | 21-24 | 2,1 | 2,8 | 3,8 |
| 2,4 | 3,7 | 6,0 | 25-28 | 2,1 | 2,8 | 3,7 |
| 2,4 | 3,5 | 5,3 | 29-30 | 2,0 | 2,8 | 3,7 |
| 2,3 | 3,4 | 5,0 | 31-34 | 2,0 | 2,7 | 3,7 |
| 2,3 | 3,3 | 4,8 | 35-42 | 2,0 | 2,7 | 3,6 |
| 2,2 | 3,2 | 4,6 | 43-62 | 2,0 | 2,7 | 3,5 |
| 2,2 | 3,1 | 4,4 | 63-175 | 2,0 | 2,6 | 3,4 |
| 2,2 | 3,1 | 4,3 | ≥176 | 2,0 | 2,6 | 3,3 |
Наиболее значимые стандартные значения критерия F (критерия Р.Фишера) на 5%-ном, 1%-ном (жирным шрифтом) уровне значимости