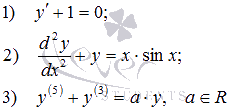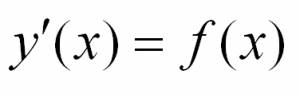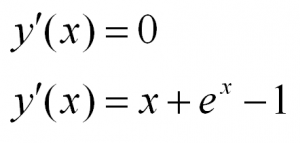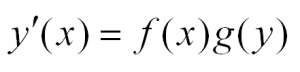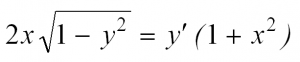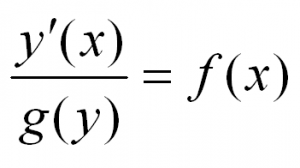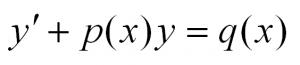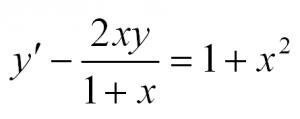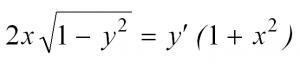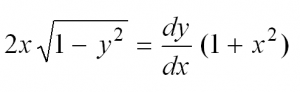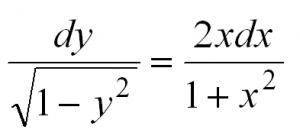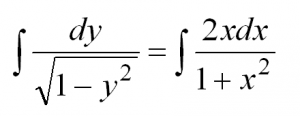Что такое дифференциальное уравнение определение

Определения и понятия теории дифференциальных уравнений.

Эта статья является отправной точкой в изучении теории дифференциальных уравнений. Здесь собраны основные определения и понятия, которые будут постоянно фигурировать в тексте. Для лучшего усвоения и понимания определения снабжены примерами.

Дифференциальное уравнение (ДУ) – это уравнение, в которое входит неизвестная функция под знаком производной или дифференциала.

Если неизвестная функция является функцией одной переменной, то дифференциальное уравнение называют обыкновенным (сокращенно ОДУ – обыкновенное дифференциальное уравнение). Если же неизвестная функция есть функция многих переменных, то дифференциальное уравнение называют уравнением в частных производных.

Максимальный порядок производной неизвестной функции, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.

Вот примеры ОДУ первого, второго и пятого порядков соответственно

В качестве примеров уравнений в частных производных второго порядка приведем

Далее мы будем рассматривать только обыкновенные дифференциальные уравнения n-ого порядка вида 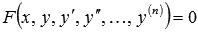или , где Ф(x, y) = 0 неизвестная функция, заданная неявно (когда возможно, будем ее записывать в явном представлении y = f(x) ).

Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения.

Решение дифференциального уравнения часто называют интегралом дифференциального уравнения.

Функции или можно назвать решением дифференциального уравнения .

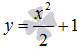
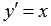
Одним из решений дифференциального уравнения является функция . Действительно, подставив эту функцию в исходное уравнение, получим тождество . Несложно заметить, что другим решением этого ОДУ является, например, . Таким образом, дифференциальные уравнения могут иметь множество решений.

Общее решение дифференциального уравнения – это множество решений, содержащее все без исключения решения этого дифференциального уравнения.

Общее решение дифференциального уравнения еще называют общим интегралом дифференциального уравнения.

Вернемся к примеру. Общее решение дифференциального уравнения имеет вид или , где C – произвольная постоянная. Выше мы указали два решения этого ОДУ, которые получаются из общего интеграла дифференциального уравнения при подстановке С = 0 и C = 1 соответственно.

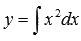
Если решение дифференциального уравнения удовлетворяет изначально заданным дополнительным условиям, то его называют частным решением дифференциального уравнения.

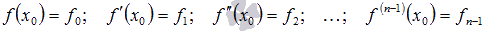
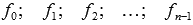
Задача Коши – это задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям , где — числа.

Краевую задачу часто называют граничной задачей.

Обыкновенное дифференциальное уравнение n-ого порядка называется линейным, если оно имеет вид 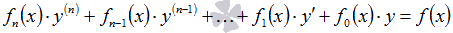, а коэффициенты есть непрерывные функции аргумента x на интервале интегрирования.

Если , то уравнение называют линейным однородным дифференциальным уравнением (ЛОДУ), в противном случае – линейным неоднородным дифференциальным уравнением (ЛНДУ).

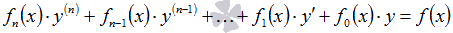
Когда коэффициенты являются постоянными функциями (то есть, некоторыми числами), то соответствующие дифференциальные уравнения называют ЛОДУ с постоянными коэффициентами (если ) или ЛНДУ с постоянными коэффициентами (при ненулевой f(x) ).

Характеристическое уравнение линейного однородного дифференциального уравнения n-ой степени с постоянными коэффициентами – это уравнение n-ой степени вида .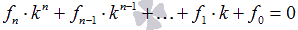

Теперь Вы знакомы с основными определениями и понятиями. Дополнительные определения будем давать по мере изложения теории. Далее рекомендуем изучить основные виды дифференциальных уравнений и методы решения.

Источник

Дифференциальное уравнение

Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных.

Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.

Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.

Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.

Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.

Содержание

Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида

или ,

где — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной , штрих означает дифференцирование по . Число называется порядком дифференциального уравнения.

Дифференциальные уравнения в частных производных

Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные. Общий вид таких уравнений можно представить в виде:

,

где — независимые переменные, а — функция этих переменных.

Примеры

— однородное дифференциальное уравнение второго порядка. Решением является семейство функций , где и — произвольные константы.

Второй закон Ньютона можно записать в форме дифференциального уравнения , где — масса тела, — его координата, — сила, действующая на тело с координатой в момент времени . Его решением является траектория движения тела под действием указанной силы.

Колебание струны задается уравнением , где — отклонение струны в точке с координатой в момент времени , параметр задает свойства струны. Это так называемое волновое уравнение.

См. также

Ссылки

Литература

Учебники

Справочники

Полезное

Смотреть что такое «Дифференциальное уравнение» в других словарях:

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ — (differential equation) Уравнение, определяющее зависимость переменной от ее собственных производных с учетом времени, которое рассматривается как непрерывная переменная. Уравнение этого типа следует отличать от разностного уравнения, в котором… … Экономический словарь

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ — уравнение, связывающее искомую функцию, ее производные (или дифференциалы) и независимые переменные, напр. dy = 2xdx. Решением или интегралом дифференциального уравнения называется функция, при подстановке которой в дифференциальное уравнение… … Большой Энциклопедический словарь

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ — ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ, уравнение, содержащее производные. Дифференциальные уравнения используются почти во всех областях ПРИКЛАДНОЙ МАТЕМАТИКИ. см. также ИСЧИСЛЕНИЕ … Научно-технический энциклопедический словарь

дифференциальное уравнение — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN differential equation … Справочник технического переводчика

дифференциальное уравнение — уравнение, связывающее искомую функцию, её производные (или дифференциалы) и независимые переменные, например dy = 2xdx. Решением или интегралом дифференциального уравнения называется функция, при подстановке которой в дифференциальном уравнении… … Энциклопедический словарь

дифференциальное уравнение — diferencialinė lygtis statusas T sritis automatika atitikmenys: angl. differential equation vok. Differentialgleichung, f rus. дифференциальное уравнение, n pranc. équation différentielle, f … Automatikos terminų žodynas

дифференциальное уравнение — diferencialinė lygtis statusas T sritis fizika atitikmenys: angl. differential equation vok. Differentialgleichung, f rus. дифференциальное уравнение, n pranc. équation différentielle, f … Fizikos terminų žodynas

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ — уравне ние, связывающее искомую функцию, её производные (или дифференциалы) и независимые переменные, напр. dy = 2xdx. Решением или интегралом Д. у. наз. ф ция, при подстановке к рой в Д. у. последнее обращается в тождество; в приведённом примере … Естествознание. Энциклопедический словарь

Дифференциальное уравнение в частных производных — (частные случаи также известны как уравнения математической физики, УМФ) дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные. Содержание 1 Введение 2 История … Википедия

Источник

Виды дифференциальных уравнений

Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.

В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.

Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.

Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.

Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».

Дифференциальные уравнения первого порядка

Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )

Начнем с примеров таких уравнений.

Приведем примеры подобных дифференциальных уравнений:

Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )

Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫ f ( y ) d y = ∫ f ( x ) d x

К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:

В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.

Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».

Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )

Приведем примеры таких уравнений.

Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a

Приведем примеры подобных уравнений.

К числу дифференциальных уравнений Бернулли можно отнести:

Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.

Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».

Дифференциальные уравнения второго порядка

Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:

исходного уравнения. Получаем: y = y 0 + y

Способ нахождения y 0 мы рассмотрели в предыдущем пункте. Найти частное решение y

Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )

Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.

Частные решения мы можем выбрать из систем независимых функций:

Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.

Общее решение линейного неоднородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x ) мы можем найти в виде суммы y = y 0 + y

частное решение исходного дифференциального уравнения. Найти y 0 можно описанным выше способом. Определить y

нам поможет метод вариации произвольных постоянных.

Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».

Дифференциальные уравнения высших порядков

Дифференциальные уравнения, допускающие понижение порядка

d 2 y d x 2 = d p d y d y d x = d p d y p ( y ) d 3 y d x 3 = d d p d y p ( y ) d x = d 2 p d y 2 d y d x p ( y ) + d p d y d p d y d y d x = = d 2 p d y 2 p 2 ( y ) + d p d y 2 p ( y )
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.

Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».

Решение уравнений данного вида предполагает выполнение следующих простых шагов:

— частное решение неоднородного дифференциального уравнения.

Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y

целесообразно использовать метод вариации произвольных постоянных.

Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».

Найти решение ЛНДУ высших порядков можно благодаря сумме y = y 0 + y

— частное решение неоднородного дифференциального уравнения.

После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y = y 0 + y

Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».

Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2

Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.

Источник

Дифференциальные уравнения для «чайников». Примеры решения

Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?

Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.

Основные понятия теории дифференциальных уравнений

Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.

Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.

Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.

Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.

Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.

Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.

Порядок дифференциального уравнения определяется наивысшим порядком производных, входящих в него.

Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.

Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:

Решить такое уравнение можно, просто проинтегрировав его правую часть.

Примеры таких уравнений:

Уравнения с разделяющимися переменными

В общем виде этот тип уравнений выглядит так:

Решая такое уравнение, нужно разделить переменные, приведя его к виду:

После этого останется проинтегрировать обе части и получить решение.

Линейные дифференциальные уравнения первого порядка

Такие уравнения имеют вид:

Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:

Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).

Для решения таких уравнений необходима определенная подготовка и взять их “с наскока” будет довольно сложно.

Пример решения ДУ с разделяющимися переменными

Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.

Сначала перепишем производную в более привычном виде:

Затем разделим переменные, то есть в одной части уравнения соберем все «игреки», а в другой – «иксы»:

Теперь осталось проинтегрировать обе части:

Интегрируем и получаем общее решение данного уравнения:

Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник