Что такое дифференциальное уравнение гармонических колебаний
Дифференциальное уравнение гармонических колебаний и его решение



Гармонические колебания
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
Колебаниями называют движения или изменения состояния, повторяющиеся через определенные промежутки времени.
Простейшим видом колебательного движения являются гармонические колебания, когда колеблющаяся величина изменяется со временем по закону синуса или косинуса.
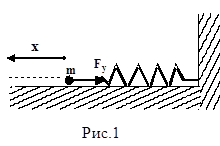 |
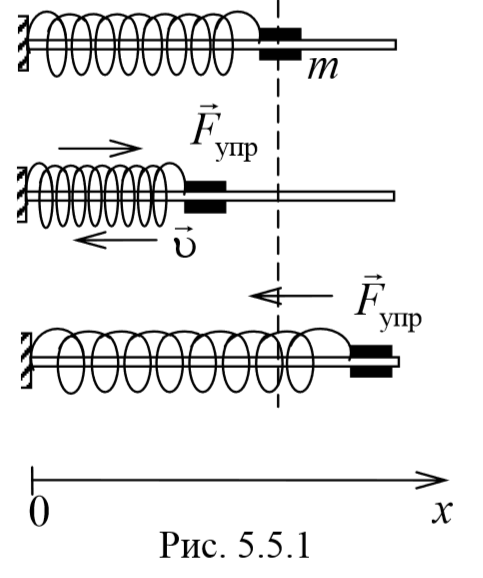
Знак “минус” указывает на противоположность направлений смещения и действия силы упругости.
Чтобы установить характер движения, т.е. зависимость х = f(t), запишем для этого случая дифференциальное уравнение, считая что в рассматриваемой системе движение определяется только наличием силы упругости:
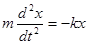
Разделим левую и правую части уравнения (1) на mи обозначим отношение положительных величин k и m через w0 2 :
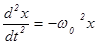
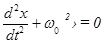
Решение дифференциального уравнения (2) имеет вид:
Зависимость скорости (v) движения материальной точки от времени при гармоническом колебании
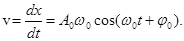
Из сравнения выражений (3) и (4) видно, что смещение и скорость гармонического колебания различаются по фазе на p /2: скорость максимальна при прохождении точкой положения равновесия (смещение равно нулю), наоборот, при максимальном смещении (равном амплитуде) скорость равна нулю.
Выражение для ускорения получается дифференцированием формулы (4):
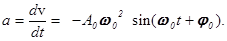
Из формул (3) и (5) следует, что смещение и ускорение изменяются в противофазе.
Лекция №7. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
5.1. Свободные гармонические колебания и их характеристики.
Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени. Наиболее важными характеристиками колебания являются: смещение, амплитуда, период, частота, циклическая частота, фаза.
Простейший вид периодических колебаний − это гармонические колебания. Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид
1) Смещение x − это величина, характеризующая колебания и равная отклонению тела от положения равновесия в данный момент времени.
2) Амплитуда колебаний А − это величина, равная максимальному отклонению тела от положения равновесия.
За период система совершает одно полное колебание.
6) Фаза колебаний ωt + φ0 − фаза указывает местоположение колеблющейся точки в данный момент времени.
5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.
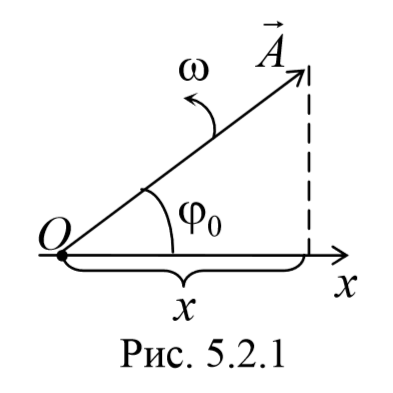
Сложение нескольких колебаний одинакового направления можно изображать графически с помощью метода векторной диаграммы.
1. Сложение одинаково направленных гармонических колебаний.
Определим начальную фазу результирующего колебания.
Из рисунка видно, что начальная фаза результирующего колебания
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, также совершает гармонические колебания в том же направлении и с той же частотой.
2. Сложение взаимно перпендикулярных гармонических колебаний.
где φ − разность фаз обоих колебаний.
Перепишем это уравнение в следующем виде
После преобразования, получим
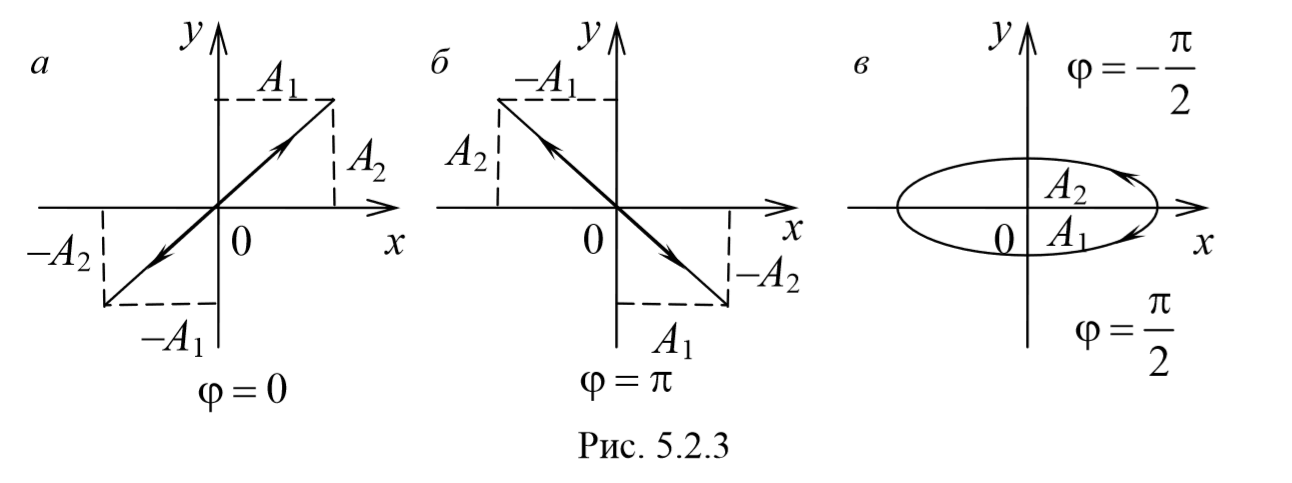
Это есть уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний и разности фаз.
Рассмотрим несколько частных случаев и определим форму траектории для них:
a) разность фаз равна нулю [φ=0]
Рассмотренные три частных случая представлены на рис. 5.2.3, а, б, в. Рис
На рис. 5.2.4 показаны фигуры Лиссажу, которые получаются при соотношении частот 1:2 и различной разности фаз колебаний.
По виду фигур можно определить неизвестную частоту по известной частоте или определить соотношение частот складываемых колебаний.
5.3. Дифференциальное уравнение гармонических колебаний и его решение.
Продифференцируем по времени уравнение гармонических колебаний
и получим выражение для скорости
Продифференцировав уравнение (2) еще раз по времени, получим выражение для ускорения
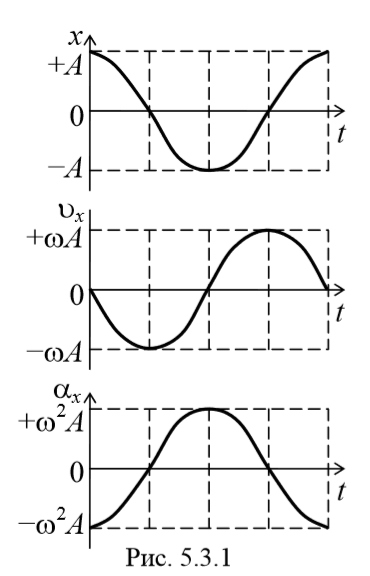
Как следует из уравнения (5.3.3), ускорение и смещение находятся в противофазе. Это означает, что в тот момент времени, когда смещение достигает наибольшего, положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Амплитуда ускорения равна Аω 2 (рис. 5.3.1).
Из выражения (5.3.3) следует дифференциальное уравнение гармонических колебаний
ω0 − собственная частота осциллятора.
5.4. Энергия гармонических колебаний.
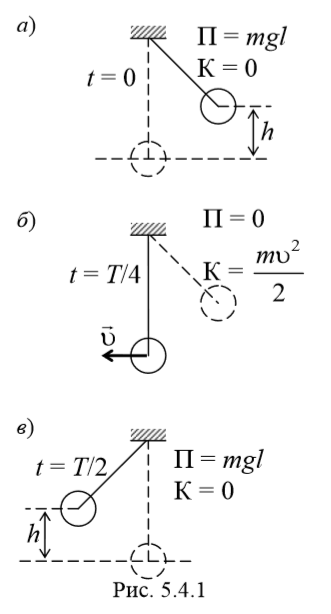
В процессе колебаний происходит превращение кинетической энергии в потенциальную энергию и обратно (рис. 5.4.1). В момент наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего наибольшего значения. Далее при движении к положению равновесия потенциальная энергия уменьшается, при этом кинетическая энергия возрастает. При прохождении через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в этот момент достигает своего наибольшего значения. Далее при движении к точке наибольшего отклонения происходит уменьшение кинетической и увеличение потенциальной энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана нулю. И т. д.
Потенциальная энергия тела, совершающего гармонические колебания равна
Кинетическая энергия тела, совершающего гармонические колебания равна
Таким образом, полная энергия гармонического колебания, состоящая из суммы кинетической и потенциальной энергий, определяется следующим образом
Следовательно, полная энергия гармонического колебания
оказывается постоянной в случае гармонических колебаний.
Найдем среднее значение потенциальной энергии за период колебания
Аналогично получается для среднего значение кинетической энергии
Таким образом, и потенциальная, и кинетическая энергии изменяются относительно своих средних значений по гармоническому закону с частотой 2ω и амплитудой ωt kA 2
5.5. Пружинный, математический и физический маятники.
Рассмотрим несколько простейших систем, совершающих свободные гармонические колебания.
Сравнивая уравнения (5.3.7) и (5.5.2) получаем, что пружинный маятник совершает гармонические колебания с частотой
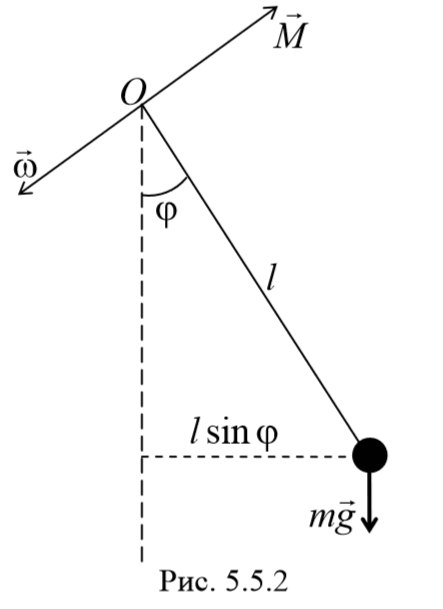
То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой
Период колебаний математического маятника
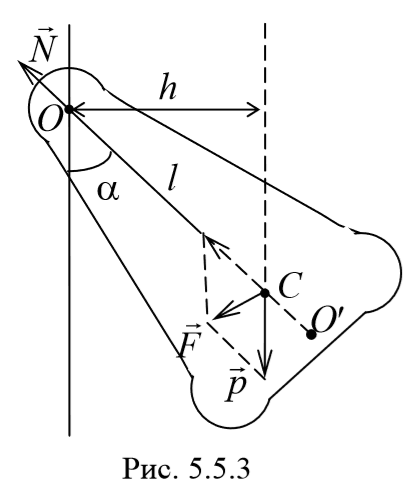
Согласно основному уравнению динамики вращательного движения получаем
где I − момент инерции маятника относительно оси, проходящей через точку подвеса.
То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой
Период колебаний математического маятника
будет иметь такой же период колебаний, что и данный физический маятник.
Величина lпр (отрезок OO′) называется приведенной длиной физического маятника − это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, и лежащая на расстоянии приведенной длины от оси вращения, называется центром качания (О′) физического маятника. Точка подвеса О и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.
Гармонические колебания
9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Механические колебания
Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.
Колебания делятся на два вида: свободные и вынужденные.
Свободные колебания
Это колебания, которые происходят под действием внутренних сил в колебательной системе.
Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.
Вынужденные колебания
А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.
Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.
Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.
Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.
Автоколебания
Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.
У автоколебательной системы есть три важных составляющих:
Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.
Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.
Характеристики колебаний
Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение характеризуется величинами: период, частота, амплитуда, фаза колебаний.
Формула периода колебаний
T = t/N
N — количество колебаний [-]
Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.
Формула частоты
ν = N/t = 1/T
N — количество колебаний [-]
Она используется в уравнении гармонических колебаний:
Гармонические колебания
Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:
Уравнение гармонических колебаний
x — координата в момент времени t [м]
t — момент времени [с]
2πνtв этом уравнении — это фаза. Ее обозначают греческой буквой φ
Фаза колебаний
t — момент времени [с]
Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.
Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.
На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.
Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.
Математический маятник
Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.
Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.
Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:
Формула периода колебания математического маятника
g — ускорение свободного падения [м/с^2]
На планете Земля g = 9,8 м/с2
Пружинный маятник
Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.
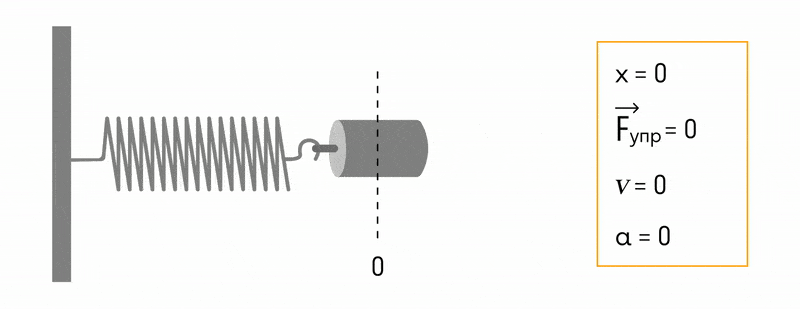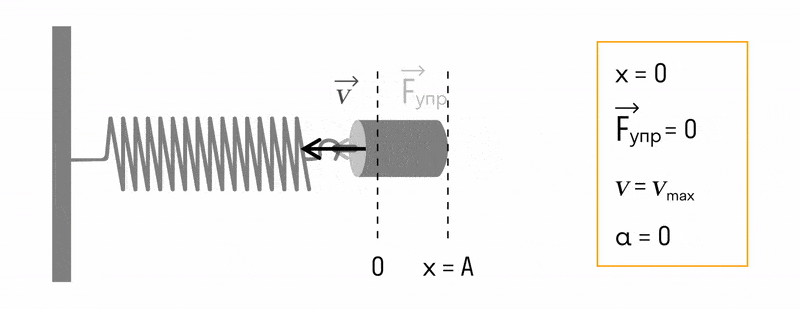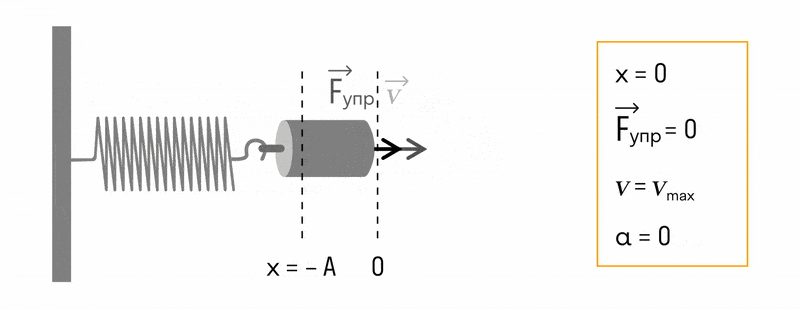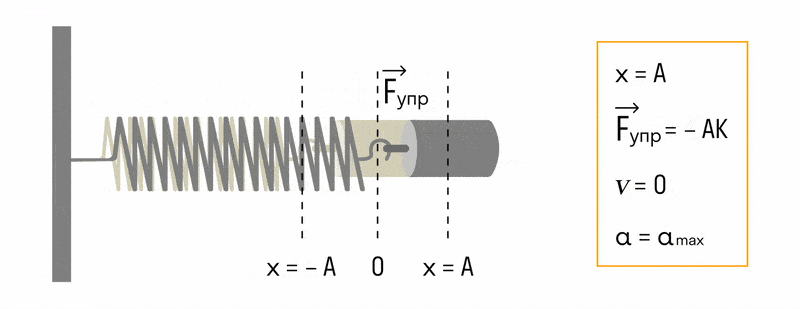
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.




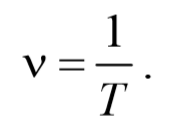
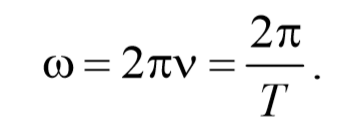
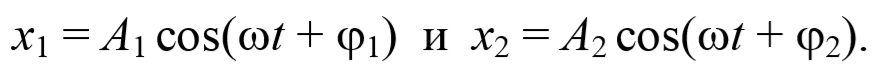
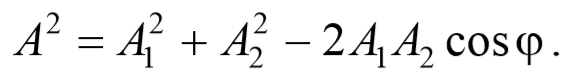
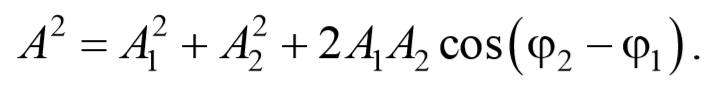
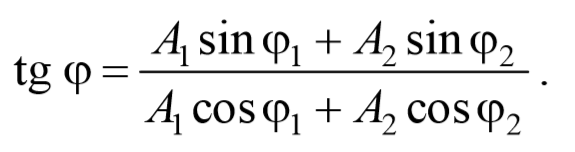
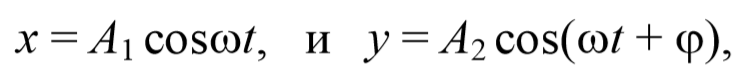
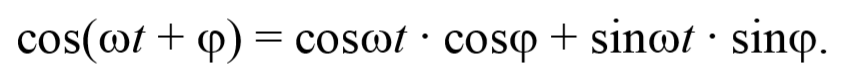
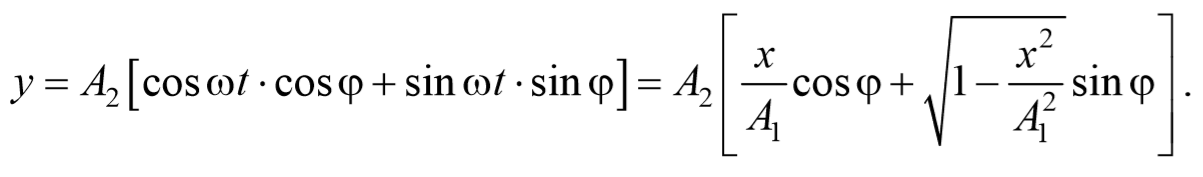
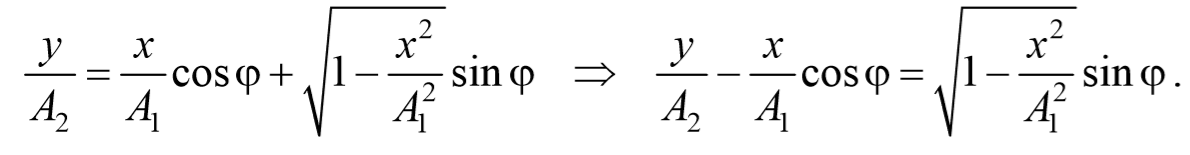
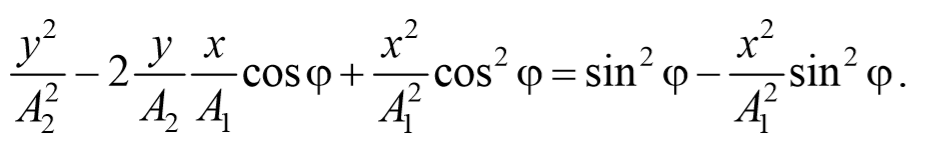
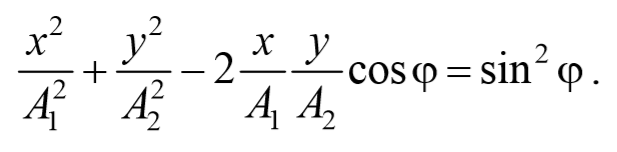
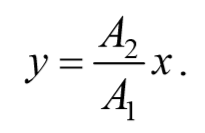
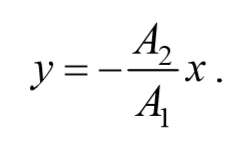
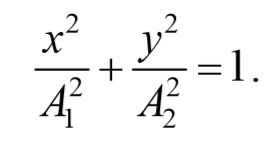

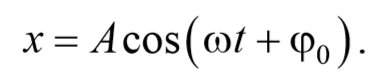
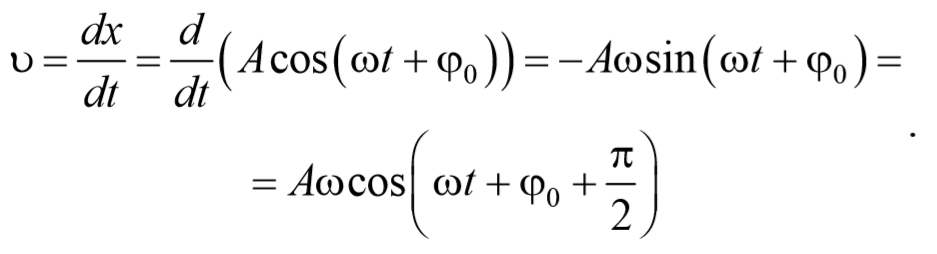

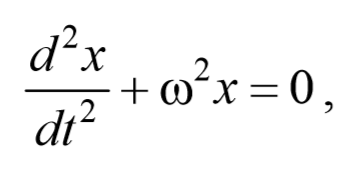
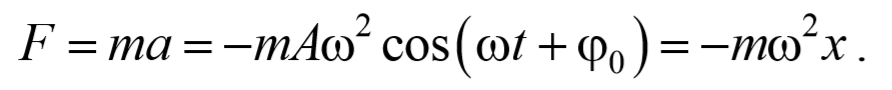
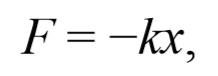
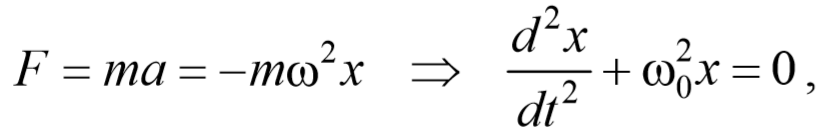
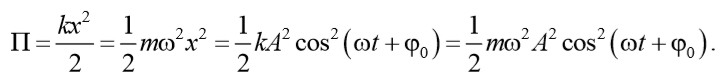

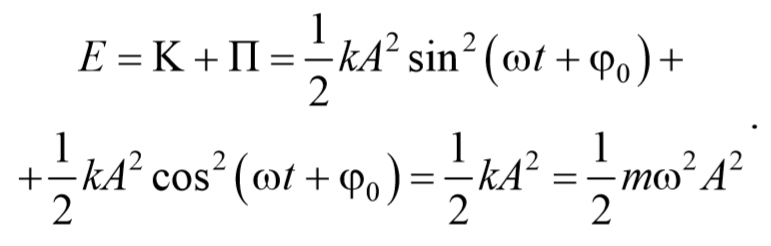
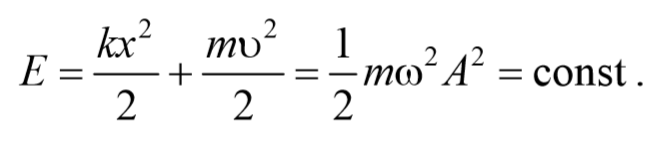
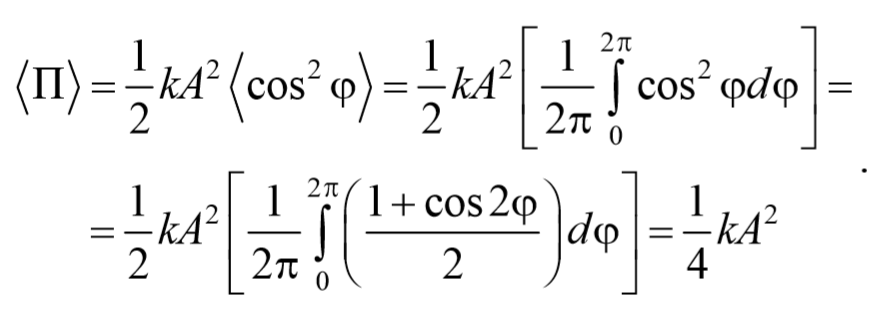
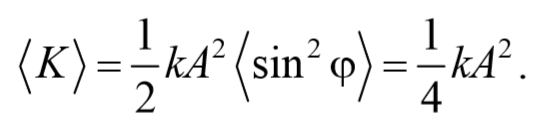
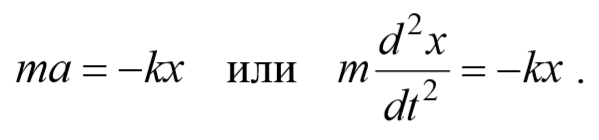
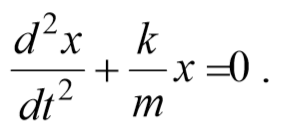
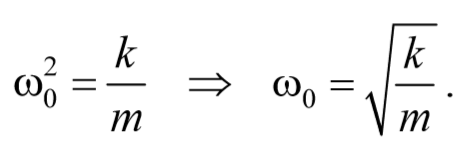
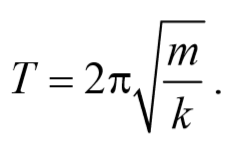
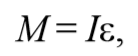
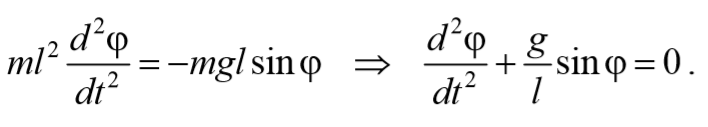
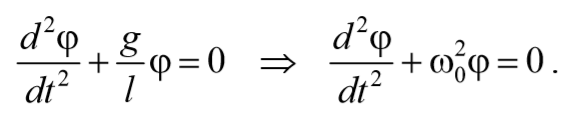
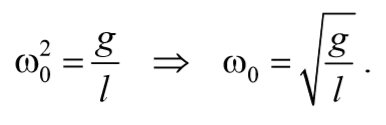
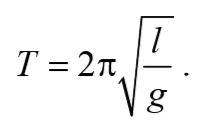
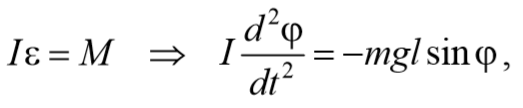
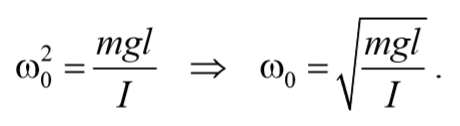
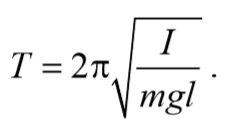
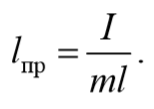








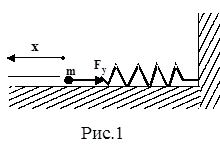
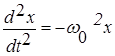 или
или 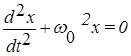 . (2)
. (2) найдем, взяв производную по времени от формулы (3):
найдем, взяв производную по времени от формулы (3):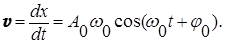 (4)
(4)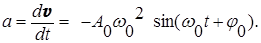 (5)
(5)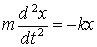 , или
, или 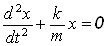 .
. . Тогда получим
. Тогда получим
 ,
,
 , получим:
, получим: .
.



 ;
;  ;
; 




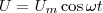



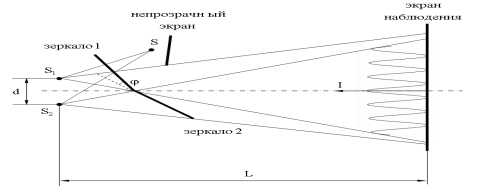 В классической электродинамике, свет рассматривается как электромагнитная волна, которая описывается уравнениями Максвелла. Световые волны, падающие на диэлектрик вызывают малые колебания диэлектрической поляризации в отдельных атомах, в результате чего каждая частица излучает вторичные волны во всех направлениях.
В классической электродинамике, свет рассматривается как электромагнитная волна, которая описывается уравнениями Максвелла. Световые волны, падающие на диэлектрик вызывают малые колебания диэлектрической поляризации в отдельных атомах, в результате чего каждая частица излучает вторичные волны во всех направлениях.