Что такое высота дерева
Измерение высоты дерева
Измерение высоты дерева
Высота дерева определяется как вертикальное расстояние между наиболее высокой точкой кроны и поверхностью земли. Она отличается от длины дерева, которая представляет собой длину ствола от поверхности земли до вершины дерева (Рис. 1). Измерения следует по возможности проводить с точностью до 0,1 м, хотя этот уровень точности не может быть достигнут для крупных деревьев.
Рекомендуется отмечать место (например, расстояние от дерева и азимут) с которого проводится измерение, чтобы проводить все последующие измерения с той же позиции. Эти же точки измерения можно выметить в натуре на земле. Хотя считается, что условия обозреваемости могут меняться через 10-20- лет (рост подроста, развитие крон. ), эта процедура является одним из способов ограничения ошибок измерения.

Совет : в некоторых случаях (например, оттирание периферических побегов, побегов поросли) верхушкой считают самую высокую «живую» почку кроны. Хотя зимой не так просто увидеть вершину дерева во время измерений высоты листопадных видов, но это
позволит отличить вершину от сухих мертвых ветвей, которые весной обычно отламываются.
Совет : Для наклоненных деревьев рекомендуется измерять высоту перпендикуляра от
самой верхней точки кроны до земли в направлении наклона дерева.
Совет : В случае, когда насаждение располагаемся на склоне (> 6°), рекомендуется измерять
высоту дерева на уровне основания дерева (той же высоте над уровнем моря) или выше.
2 способ
Измерение проводят вдвоём. Один человек становится рядом с деревом, а другой, с хорошим глазомером, отойдя на некоторое расстояние, чтобы охватить взглядом, всё дерево от комля до вершины, «откладывает» на глаз, сколько человек данного роста «укладывается» по всей длине ствола. При этом рациональнее каждый раз откладывать расстояние, вдвое больше, чем предыдущее, т.е. мысленно отложить сначала высоту двух «человечков», затем прибавить к ним ещё двух, затем – ещё четырёх, затем ещё восьми и т.д. (т.е. по схеме 1 – 2 – 4 – 8 – 16). С точки зрения человеческого глазомера это проще и точнее. Зная рост «человечка» можно подсчитать высоту дерева.
3 способ
Измерение высоты дерева при помощи тени
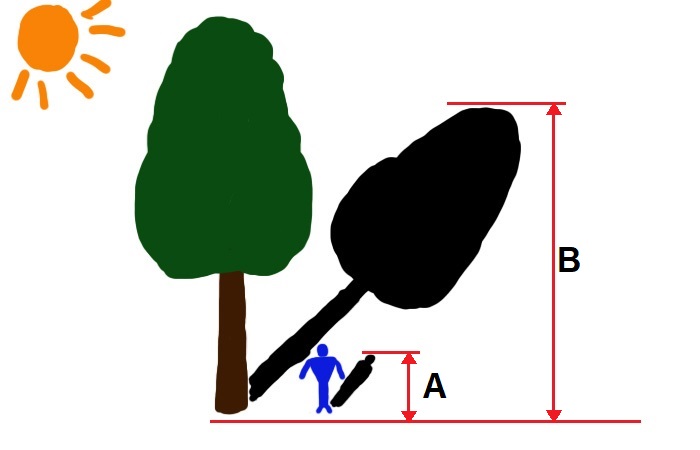
В солнечный день для определения высоты дерева можно воспользоваться отбрасываемой им тенью. Измерив свою тень или тень какого-нибудь шеста, вы можете вычислить искомую высоту из пропорции АВ:аb = ВС:bс
II.4. 3. Методика определения возраста дерева
Все что нужно знать о древовидных структурах данных
Jul 1, 2018 · 14 min read
Деревья прекрасны. Вот рисунок, который я сделал ребенком
Когда вы впервые учитесь кодировать, общепринято изучать массивы в качестве «основной структуры данных».
В конце концов, вы также изучаете хэш-таблицы. Для получения степени по «Компьютерным наукам» (Computer Science) вам придется походить на занятия по структурам данных, на которых вы узнаете о связанных списках, очередях и стеках. Эти структуры данных называются «линейными», поскольку они имеют логические начало и завершение.
Однако в самом начале и зучения деревьев и графов мы можем оказаться слегка сбитыми с толку. Нам привычно хранить данные линейным способом, а эти две структуры хранят данные совершенно иначе.
Данная статья поможет вам лучше понять древовидные структуры данных и устранить все недоразумения на их счет.
Из этой статьи вы узнаете:
Давайте начнем наше учебное путешествие 🙂
Определения
Когда вы только начинаете изучать программирование, обычно бывает проще понять, как строятся линейные структуры данных, чем более сложные структуры, такие как деревья и графы.
Деревья являются широко известными нелинейными структурами. Они хранят данные не линейным способом, а упорядочивают их иерархически.
Давайте вплотную займемся реальными примерами
Что я имею в виду, когда я говорю иерархически?
Представьте себе генеалогическое древо отношений между поколениями: бабушки и дедушки, родители, дети, братья и сестры и т.д. Мы обычно организуем семейные деревья иерархически.
Мое фамильное дерево
Приведенный рисунок — это мое фамильное древо. Тосико, Акикадзу, Хитоми и Такеми — мои дедушки и бабушки.
Тошиаки и Джулиана — мои родители.
ТК, Юдзи, Бруно и Кайо — дети моих родителей (я и мои братья).
Структура организации — еще один пример иерархии.
Структура компании является примером иерархии
В HTML, объектная модель документа (DOM) представляется в виде дерева.
Объектная модель документа (DOM)
Техническое определение
Дерево представляет собой набор объектов, называемых узлами. Узлы соединены ребрами. Каждый узел содержит значение или данные, и он может иметь или не иметь дочерний узел.
Первый узел дерева называется корнем. Если этот корневой узел соединен с другим узлом, тогда корень является родительским узлом, а связанный с ним узел — дочерним.
Все узлы дерева соединены линиями, называемыми ребрами. Это важная часть деревьев, потому что она управляет связью между узлами.
Листья — это последние узлы на дереве. Это узлы без потомков. Как и в реальных деревьях, здесь имеется корень, ветви и, наконец, листья.
Другими важными понятиями являются высота и глубина.
Высота дерева — это длина самого длинного пути к листу.
Глубина узла — это длина пути к его корню.
Справочник терминов
Бинарные деревья
Теперь рассмотрим особый тип деревьев, называемых бинарными или двоичными деревьями.
“В информатике бинарным (двоичным) деревом называется иерархическая структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками.” — Wikipedia
Рассмотрим пример бинарного дерева.
Давайте закодируем бинарное дерево
Как мы реализуем простое двоичное дерево, которое инициализирует эти три свойства?
Вот наш двоичный класс дерева.
Когда мы создаем наш узел, он не имеет потомков. Просто есть данные узла.
Давайте это проверим:
Перейдем к части вставки. Что нам нужно здесь сделать?
Мы реализуем метод вставки нового узла справа и слева.
Давайте это нарисуем 🙂
Вот программный код:
Еще раз, если текущий узел не имеет левого дочернего элемента, мы просто создаем новый узел и устанавливаем его в качестве left_child текущего узла. Или мы создаем новый узел и помещаем его вместо текущего левого потомка. Назначим этот левый дочерний узел в качестве левого дочернего элемента нового узла.
И мы делаем то же самое, чтобы вставить правый дочерний узел.
Но не полностью. Осталось протестировать.
Давайте построим следующее дерево:
Подытоживая изображенное дерево, заметим:
Таким образом, вот код для нашего дерева следующий:
Теперь нам нужно подумать об обходе дерева.
У нас есть два варианта: поиск в глубину (DFS) и поиск по ширине (BFS).
• Поиск в глубину (Depth-first search, DFS) — один из методов обхода дерева. Стратегия поиска в глубину, как и следует из названия, состоит в том, чтобы идти «вглубь» дерева, насколько это возможно. Алгоритм поиска описывается рекурсивно: перебираем все исходящие из рассматриваемой вершины рёбра. Если ребро ведёт в вершину, которая не была рассмотрена ранее, то запускаем алгоритм от этой нерассмотренной вершины, а после возвращаемся и продолжаем перебирать рёбра. Возврат происходит в том случае, если в рассматриваемой вершине не осталось рёбер, которые ведут в не рассмотренную вершину. Если после завершения алгоритма не все вершины были рассмотрены, то необходимо запустить алгоритм от одной из не рассмотренных вершин.
• Поиск в ширину (breadth-first search, BFS) — метод обхода дерева и поиска пути. Поиск в ширину является одним из неинформированных алгоритмов поиска. Поиск в ширину работает путём последовательного просмотра отдельных уровней дерева, начиная с узла-источника. Рассмотрим все рёбра, выходящие из узла. Если очередной узел является целевым узлом, то поиск завершается; в противном случае узел добавляется в очередь. После того, как будут проверены все рёбра, выходящие из узла, из очереди извлекается следующий узел, и процесс повторяется.
Давайте подробно рассмотрим каждый из алгоритмов обхода.
Поиск в глубину (DFS)
DFS исследует все возможные пути вплоть до некоторого листа дерева, возвращается и исследует другой путь (осуществляя, таким образом, поиск с возвратом). Давайте посмотрим на пример с этим типом обхода.
Результатом этого алгоритма будет: 1–2–3–4–5–6–7.
Давайте разъясним это подробно.
Проход в глубь дерева, а затем возврат к исходной точке называется алгоритмом DFS.
После знакомства с этим алгоритмом обхода, рассмотрим различные типы DFS-алгоритма: предварительный обход (pre-order), симметричный обход (in-order) и обход в обратном порядке (post-order).
Предварительный обход
Именно это мы и делали в вышеприведенном примере.
1. Записать значение узла.
2. Перейти к левому потомку и записать его. Это выполняется тогда и только тогда, когда имеется левый потомок.
3. Перейти к правому потомку и записать его. Это выполняется тогда и только тогда, когда имеется правый потомок.
 masterok
masterok
Мастерок.жж.рф
Хочу все знать
Никогда не знаешь, что именно пригодится завтра! Человек должен стараться овладеть как можно большим количеством разнообразных навыков. Некоторые из тех, что на первый взгляд кажутся абсолютно бесполезными, могут сыграть решающую роль в какой-нибудь жизненной ситуации, пригодившись самым неожиданным образом.
Например, мало кто знает, как можно легко и быстро измерять высоту дерева.
Метод первый – при помощи тени
Самый простой способ измерять дерево – это использовать его и свою тень. Для этого нужно встать рядом с растением и сначала отметить место, где оказались пятки, а потом отметить место до которого падала твоя тень. Полученный отрезок необходимо измерять. После этого необходимо снять мерку с тени дерева.
Два важных момента. Первый – тень должна лежать на ровной земле без уклона, в противном случае полученные данные не будут объективными и не помогут получить правильное значение. Второй – измерять тень себя-любимого и коварного дерева нужно в одно и то же время.
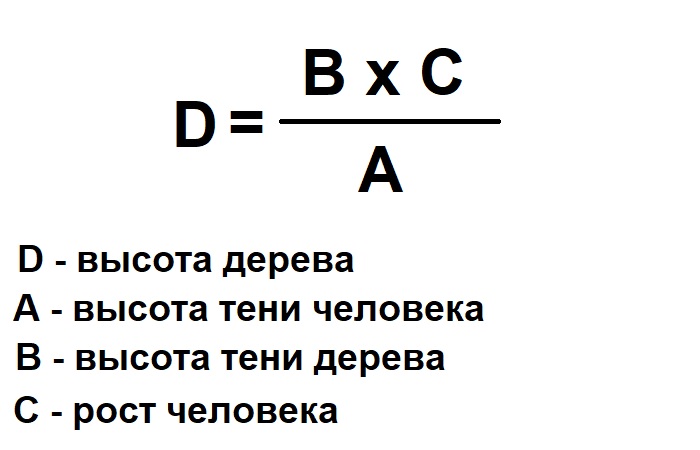
Когда все мерки будут сняты, то дело останется за малым – математическими подсчетами. Для этого умножаем длину тени дерева на высоту своего роста и полученное значение делим на высоту своей тени. Полученное значение и будет высотой дерева.
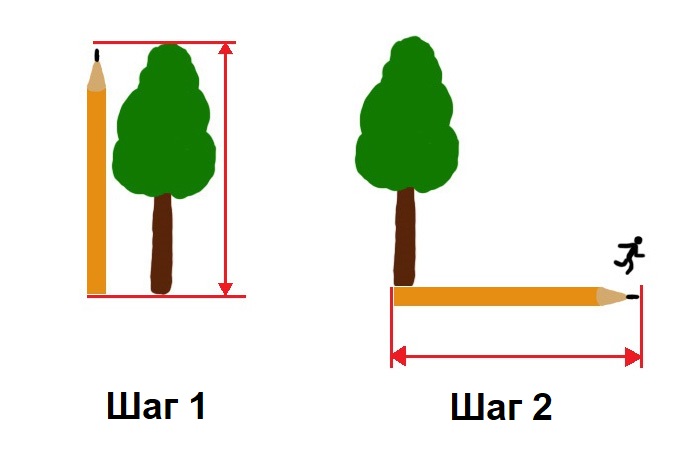
Метод второй – при помощи карандаша
Измерять высоту дерева можно еще и при помощи карандаша. Помимо пишущей принадлежности для работы понадобится еще один (а лучше два) человека. Первым делом следует взять карандаш в руку и стать таким образом, чтобы дерево было видно целиком от корней до макушки. Рядом со стволом дерева ставится человек-помощник.
Сжимаем карандаш в кулаке и вытягиваем его перед собой, прищуриваем один глаз и соотносим кончик грифеля с макушкой растения. Подвигаем ноготь большого пальца так, чтобы он оказался под основанием ствола. Далее поворачиваем кулак на 90 градусов, чтобы карандаш сал параллелен земле.
После этого человеку, стоящему у ствола, дается команда идти вдоль карандаша от дерева. Как только его силуэт достигнет грифеля, следует дать команду остановится. В итоге расстояние от ствола дерева до твоего товарища и будет высотой растения.
Ландшафтный дизайн
Опубликовано: Июль 13, 2010
Опубликовано: Июль 13, 2010
Опубликовано: Июль 13, 2010
Опубликовано: Июль 13, 2010
От: Rogov
Опубликовано: Июль 13, 2010
От: MarkA
Опубликовано: Июль 13, 2010
От: MarkA
Опубликовано: Июль 13, 2010
От: MarkA
Опубликовано: Август 3, 2010
От: MarkA
Опубликовано: Август 3, 2010
От: MarkA
Опубликовано: Август 3, 2010
От: MarkA
Опубликовано: Август 3, 2010
От: MarkA
Опубликовано: Август 3, 2010
От: MarkA
Опубликовано: Август 3, 2010
От: MarkA
Опубликовано: Август 23, 2010
От: MarkA
Опубликовано: Август 23, 2010
От: MarkA
Опубликовано: Август 23, 2010
От: MarkA
Опубликовано: Сентябрь 3, 2010
От: MarkA
Опубликовано: Сентябрь 3, 2010
От: MarkA
Опубликовано: Сентябрь 3, 2010
От: Rogov
Опубликовано: Сентябрь 3, 2010
Ручьи, речки, каналы, бассейны
От: zeta
Опубликовано: Февраль 21, 2014
Цветники цветы, клумбы, рабатки, бордюры, миксбордюры, альпийские горки, вазоны, посадка лиан
Простые способы определения высоты дерева или любого другого предмета по тени, шесту, лужице или зеркалу, прямоугольному треугольнику.
В полевых условиях иногда бывает очень важно и полезно владеть простейшими прикладными способами измерений на местности. Например способами определения высоты дерева или любого другого предмета на местности.
Простые способы определения высоты дерева или любого другого предмета по тени, шесту, лужице или зеркалу, прямоугольному треугольнику.
Высоту дерева или любого другого предмета на местности очень просто можно определить по тени, шесту, лужице или зеркальцу, и прямоугольному треугольнику.
Способ определения высоты дерева или другого предмета по своему росту и длине тени.
Если на ровном месте измерить шагами длину своей тени, а затем длину тени, отбрасываемой деревом илипредметом, то искомую высоту легко вычислить из пропорции :
АК/ак = КЕ/ке
где АК — высота дерева (В), КЕ — тень дерева (D), ак — ваш рост (b), ке — ваша тень (d).
Например длина вашей тени d равна трем шагам, тень дерева D равна девяти шагам, то есть тень дерева длиннее вашей тени в три раза. Если принять ваш рост за 1,5 метра, то высота дерева будет В = 1,5 х 3 = 4,5 метра.
Способ определения высоты дерева или другого предмета по шесту и своему росту.
Этот же способ можно применить при пасмурной погоде, когда тени от предметов не видны. В этом случае для измерения нужно взятьшест, равный длине вашего роста. Шест этот надо установить на таком расстоянии от дерева, чтобы лежа можно было видеть верхушку дерева на одной прямой линии с верхней точкой шеста. Тогда высота дерева равна расстоянию от вашей головы до основания дерева, то есть АС = ВС.
Способ определения высоты дерева или другого предмета по лужице или зеркальцу.
По лужице, зеркальцу илигелиографу высоту дерева или любого другого предмета на местности, можно измерять следующим образом. Станьте так, чтобы лужица поместилась между вами и деревом (В). Найдите точку, из которой видна отраженная в воде вершина дерева. Измеряемоедерево будет во столько раз выше вас, во сколько расстояние от него до лужицы (ВО) больше расстояния от лужицы до вас (АО). Вместо лужицы также можно воспользоваться зеркальцем, положив его горизонтально так, чтобы увидеть вершину дерева.
Способ определения высоты дерева или другого предмета с помощью прямоугольного треугольника с двумя острыми углами по 45 градусов.
С помощью прямоугольного треугольника с двумя острыми углами по 45 градусов, высоту дерева или другогопредмета определяют так. Отходя от дерева на некоторое расстояние и прикладывая треугольник к глазам так, чтобы один из его катетов был параллелен оси дерева, второй — параллелен земной поверхности, а гипотенуза представляла собой линию визирования.
Затем добиваются такого положения, чтобы линия визирования прошла через вершину дерева. В этом случае высота дерева D равна расстоянию от наблюдателя до дерева и плюс рост наблюдателя.
По материалам книги «Карта и компас мои друзья».
Клименко А.И.














 masterok
masterok