Что такое высота дерева в информатике
Какой граф называется деревом? Что такое дерево в информатике?
Содержание:
Граф-дерево является очень распространенным видом графов в информатике. Они нужны для хранения какой-либо информации в нелинейной структуре в иерархическом порядке.
Граф — это структура, состоящая из множества вершин, соединенных ребрами. Все в своей жизни видели транспортные схемы (передвижение автобусов или метро). Если эти схемы смоделировать в компьютере, то остановки и станции — это будут вершины графа, а маршрут транспорта между остановками/станциями — ребра графа.
В зависимости от того, каким образом расположены вершины, какое отношение между ними и каким способом они соединяются между собой ребрами, различают различные виды графов. Граф-дерево — это всего лишь один из множества видов графов.
Граф-дерево
Самое главное, все имена вы соединяли линиями зависимости между собой. Например, свое имя соединили с именами братьев и сестер и с именами своих родителей. Имена ваших родителей вы соединили с именами их братьев и сестер и с их родителями и т. д.
В информатике, граф-дерево выглядит точно так же, как и ваше генеалогическое дерево, только вместо имен — вершины, а вместо линий, связывающих имена — ребра.
Охарактеризовать граф-дерево в информатике можно так — это связный граф, где между двумя вершинам есть единственный связный путь. Вернемся к нашему дереву. Ваше имя будет связано линиями только с вашими родителями и вашими братьями/сестрами, с другими именами дерева у вас нет прямой связи. Например, с вашими дядями, тетями, бабушками и дедушками вы будете связаны только через ваших родителей, а не напрямую. А с вашей прабабушкой или вашим прадедушкой вы будете связаны только через родителей и бабушек с дедушками.
То есть граф-дерево в информатике следует строгой иерархии — одни элементы находятся «наверху» графа и будут называться «корнем дерева», другие элементы будут чуть ниже и будут называться «потомками», от «потомков» будут исходить «листья» — это те вершины, которые не имеют «потомков». Любой элемент верхнего уровня по отношению к нижнему уровню будет называться «предком».
Вернемся к нашему генеалогическому дереву. Бабушка с дедушкой (или прабабушка с прадедушкой, то есть в зависимости до какой глубины своих предков вы дойдете) будут корнем вашего граф-дерева (либо подкорнем, если у вас в корне будут прабабушка с прадедушкой). Ваши родители — это «потомки» вашего граф-дерева и бабушка с дедушкой для них будут «предками» вашего дерева. Вы будете «листьями» граф-дерева, потому что у вас пока нет своего потомства, как только у вас появятся дети, то вы станете «потомками» графа, а ваши дети «листьями». Ваши родители для вас будут «предками» графа.
B-tree
Введение
Деревья представляют собой структуры данных, в которых реализованы операции над динамическими множествами. Из таких операций хотелось бы выделить — поиск элемента, поиск минимального (максимального) элемента, вставка, удаление, переход к родителю, переход к ребенку. Таким образом, дерево может использоваться и как обыкновенный словарь, и как очередь с приоритетами.
Основные операции в деревьях выполняются за время пропорциональное его высоте. Сбалансированные деревья минимизируют свою высоту (к примеру, высота бинарного сбалансированного дерева с n узлами равна log n). Большинство знакомо с такими сбалансированными деревьями, как «красно-черное дерево», «AVL-дерево», «Декартово дерево», поэтому не будем углубляться.
В чем же проблема этих стандартных деревьев поиска? Рассмотрим огромную базу данных, представленную в виде одного из упомянутых деревьев. Очевидно, что мы не можем хранить всё это дерево в оперативной памяти => в ней храним лишь часть информации, остальное же хранится на стороннем носителе (допустим, на жестком диске, скорость доступа к которому гораздо медленнее). Такие деревья как красно-черное или Декартово будут требовать от нас log n обращений к стороннему носителю. При больших n это очень много. Как раз эту проблему и призваны решить B-деревья!
B-деревья также представляют собой сбалансированные деревья, поэтому время выполнения стандартных операций в них пропорционально высоте. Но, в отличие от остальных деревьев, они созданы специально для эффективной работы с дисковой памятью (в предыдущем примере – сторонним носителем), а точнее — они минимизируют обращения типа ввода-вывода.
Структура
При построении B-дерева применяется фактор t, который называется минимальной степенью. Каждый узел, кроме корневого, должен иметь, как минимум t – 1, и не более 2t – 1 ключей. Обозначается n[x] – количество ключей в узле x.
Все листья B-дерева должны быть расположены на одной высоте, которая и является высотой дерева. Высота B-дерева с n ≥ 1 узлами и минимальной степенью t ≥ 2 не превышает logt(n+1). Это очень важное утверждение (почему – мы поймем чуть позже)!
h ≤ logt((n+1)/2) — логарифм по основанию t.
Операции, выполнимые с B-деревом
Как упоминалось выше, в B-дереве выполняются все стандартные операции по поиску, вставке, удалению и т.д.
Поиск
Операция поиска выполняется за время O(t logt n), где t – минимальная степень. Важно здесь, что дисковых операций мы совершаем всего лишь O(logt n)!
Добавление
В отличие от поиска, операция добавления существенно сложнее, чем в бинарном дереве, так как просто создать новый лист и вставить туда ключ нельзя, поскольку будут нарушаться свойства B-дерева. Также вставить ключ в уже заполненный лист невозможно => необходима операция разбиения узла на 2. Если лист был заполнен, то в нем находилось 2t-1 ключей => разбиваем на 2 по t-1, а средний элемент (для которого t-1 первых ключей меньше его, а t-1 последних больше) перемещается в родительский узел. Соответственно, если родительский узел также был заполнен – то нам опять приходится разбивать. И так далее до корня (если разбивается корень – то появляется новый корень и глубина дерева увеличивается). Как и в случае обычных бинарных деревьев, вставка осуществляется за один проход от корня к листу. На каждой итерации (в поисках позиции для нового ключа – от корня к листу) мы разбиваем все заполненные узлы, через которые проходим (в том числе лист). Таким образом, если в результате для вставки потребуется разбить какой-то узел – мы уверены в том, что его родитель не заполнен!
На рисунке ниже проиллюстрировано то же дерево, что и в поиске (t=3). Только теперь добавляем ключ «15». В поисках позиции для нового ключа мы натыкаемся на заполненный узел (7, 9, 11, 13, 16). Следуя алгоритму, разбиваем его – при этом «11» переходит в родительский узел, а исходный разбивается на 2. Далее ключ «15» вставляется во второй «отколовшийся» узел. Все свойства B-дерева сохраняются!
Операция добавления происходит также за время O(t logt n). Важно опять же, что дисковых операций мы выполняем всего лишь O(h), где h – высота дерева.
Удаление
Удаление ключа из B-дерева еще более громоздкий и сложный процесс, чем вставка. Это связано с тем, что удаление из внутреннего узла требует перестройки дерева в целом. Аналогично вставке необходимо проверять, что мы сохраняем свойства B-дерева, только в данном случае нужно отслеживать, когда ключей t-1 (то есть, если из этого узла удалить ключ – то узел не сможет существовать). Рассмотрим алгоритм удаления:
1)Если удаление происходит из листа, то необходимо проверить, сколько ключей находится в нем. Если больше t-1, то просто удаляем и больше ничего делать не нужно. Иначе, если существует соседний лист (находящийся рядом с ним и имеющий такого же родителя), который содержит больше t-1 ключа, то выберем ключ из этого соседа, который является разделителем между оставшимися ключами узла-соседа и исходного узла (то есть не больше всех из одной группы и не меньше всех из другой). Пусть это ключ k1. Выберем ключ k2 из узла-родителя, который является разделителем исходного узла и его соседа, который мы выбрали ранее. Удалим из исходного узла нужный ключ (который необходимо было удалить), спустим k2 в этот узел, а вместо k2 в узле-родителе поставим k1. Чтобы было понятнее ниже представлен рисунок (рис.1), где удаляется ключ «9». Если же все соседи нашего узла имеют по t-1 ключу. То мы объединяем его с каким-либо соседом, удаляем нужный ключ. И тот ключ из узла-родителя, который был разделителем для этих двух «бывших» соседей, переместим в наш новообразовавшийся узел (очевидно, он будет в нем медианой).
Рис. 1.
2)Теперь рассмотрим удаление из внутреннего узла x ключа k. Если дочерний узел, предшествующий ключу k содержит больше t-1 ключа, то находим k1 – предшественника k в поддереве этого узла. Удаляем его (рекурсивно запускаем наш алгоритм). Заменяем k в исходном узле на k1. Проделываем аналогичную работу, если дочерний узел, следующий за ключом k, имеет больше t-1 ключа. Если оба (следующий и предшествующий дочерние узлы) имеют по t-1 ключу, то объединяем этих детей, переносим в них k, а далее удаляем k из нового узла (рекурсивно запускаем наш алгоритм). Если сливаются 2 последних потомка корня – то они становятся корнем, а предыдущий корень освобождается. Ниже представлен рисунок (рис.2), где из корня удаляется «11» (случай, когда у следующего узла больше t-1 ребенка).
Рис.2.
Операция удаления происходит за такое же время, что и вставка O(t logt n). Да и дисковых операций требуется всего лишь O(h), где h – высота дерева.
Итак, мы убедились в том, что B-дерево является быстрой структурой данных (наряду с такими, как красно-черное, АВЛ). И еще одно важное свойство, которое мы получили, рассмотрев стандартные операции, – автоматическое поддержание свойства сбалансированности – заметим, что мы нигде не балансируем его специально.
Базы Данных
Проанализировав, вместе со скоростью выполнения, количество проведенных операций с дисковой памятью, мы можем сказать, что B-дерево несомненно является более выгодной структурой данных для случаев, когда мы имеем большой объем информации.
Очевидно, увеличивая t (минимальную степень), мы увеличиваем ветвление нашего дерева, а следовательно уменьшаем высоту! Какое же t выбрать? — Выбираем согласно размеру оперативной памяти, доступной нам (т.е. сколько ключей мы можем единовременно просматривать). Обычно это число находится в пределах от 50 до 2000. Разберёмся, что же дает нам ветвистость дерева на стандартном примере, который используется во всех статьях про B-tree. Пусть у нас есть миллиард ключей, и t=1001. Тогда нам потребуется всего лишь 3 дисковые операции для поиска любого ключа! При этом учитываем, что корень мы можем хранить постоянно. Теперь видно, на сколько это мало!
Также, мы читаем не отдельные данные с разных мест, а целыми блоками. Перемещая узел дерева в оперативную память, мы перемещаем выделенный блок последовательной памяти, поэтому эта операция достаточно быстро работает.
Соответственно, мы имеем минимальную нагрузку на сервер, и при этом малое время ожидания. Эти и другие описанные преимущества позволили B-деревьям стать основой для индексов, базирующихся на деревьях в СУБД.
Study & Dev О программировании и не только
Структуры данных и алгоритмы. Теория. Деревья. Основные алгоритмы над деревьями
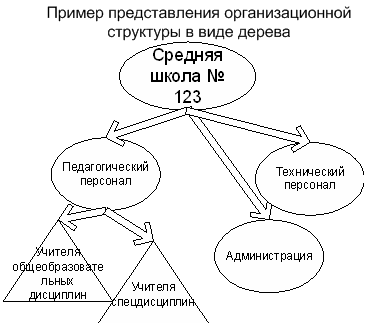
Дерево – это АТД (абстрактный тип данных) для хранения информационных элементов имеющих нелинейные отношения. За исключением элемента, который находится во главе дерева, каждый элемент имеет родителя, а также ноль или более дочерних элементов. Также говорят что дерево – это множество элементов, среди которых есть один выделенный который называется корнем, а остальные содержатся в N непересекающихся подмножествах, которые называются поддеревьями. Очевидно что дерево относится к классу динамических структур данных наряду с нам уже знакомыми стеком, очередями. С помощью дерева можно представить, например, следующую организационную структуру:
Наиболее известным классическим примером деревьев является генеалогическое дерево.
Также в качестве примера можно привести принятую в большинстве файловых систем организацию с помощью иерархически вложенных директорий и файлов. Наиболее ярко это проявляется в О.С. linux и unix, где файловую систему представляют в виде единого дерева, которое начинается с корневой директории обозначаемой “/”.
При дальнейшем обсуждении деревьев следует условиться о терминологии. Корень дерева (root) – первый его элемент (в приведенном выше изображении это “Средняя школа # 123”). Каждый элемент данных называют узлом (node), иногда листом (leaf). Фрагмент дерева называется поддеревом (subtree) или ветвью. Узел, не имеющий отходящих от него ветвей ли поддеревьев, называются терминальным или конечным узлом (terminal node). Высота дерева (height) – определяется количеством уровней, на которых располагаются его узлы. При работе с деревьями полезно изображать их на бумаге, однако при этом всегда следует помнить, что деревья – это метод логической организации информации в памяти компьютера, не физической.
Следует помнить, что большинство операций, которые выполняются над деревьями, являются рекурсивными, т.к. деревья имеют рекурсивную структуру – каждое дерево содержит множество поддеревьев.
О деревьях можно судить как об упорядоченных или не упорядоченных. Мы говорим, что дерево упорядочено, если каждому из элементов можно сопоставить порядковый номер: 1,2,3. На рисунках упорядоченные “братья-узлы” представляются слева направо.
Пример упорядоченного дерева: книга. Книга имеет древовидную структуру с делением на разделы, каждый из которых состоит из множества тем, а тема включает отдельные вопросы. Каждый из вопросов также можно разделить на элементарные части – абзацы, картинки, таблицы. Очевидно, что эти элементы имеют четкий порядок следования, нарушение которого приводит к потере смысла книги.
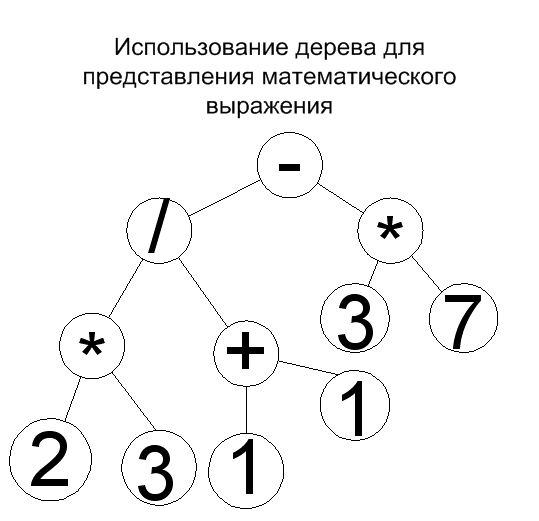
С помощью двоичного дерева можно легко представить арифметическое выражение с использованием бинарных операций.
Например, для выражения: (2*3)/(1+1)-(3*7) можно построить следующее дерево:
Для каждого узла дерева можно определить понятие глубины. Допустим, V – узел дерева. Глубина узла выражается количество предков V, за исключением самого V. По определению глубина корня равна нулю.
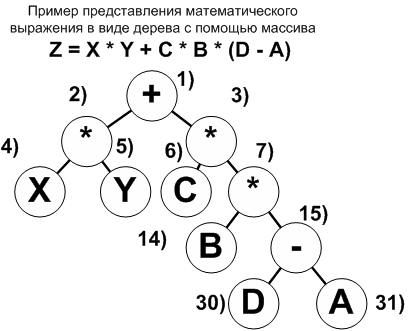
Способы представления деревьев: Представление дерева с помощью массива
Очень важно, что если дерево не полное, то отсутствующим элементам назначаются номера и для них выделяется место в массиве, просто в ячейке с номером “8, 9, 13, 29” и других (согласно приведенному изображению дерева математического выражения) ничего не хранится.
Представление дерева с помощью ссылок
В случае множественного дерева (каждый узел может иметь произвольное количество потомков) возможно, воспользоваться подобным объявлением:
В данном примере DATA_TYPE – тип данных соответствующий хранимому в дереве, например, если у нас дерево математического выражения, то это может быть число или знак арифметической операции. Если дерево служит для хранения генеалогической информации – то в качестве типа каждого узла может быть строка с именем человека, или даже произвольная структура или класс CHuman, описывающий кого-то из предков. Обратите внимание на другое, в структуре присутствует ссылка на узел дерева который является родительским, в общем случае это не требуется, однако при решении многих задач поиска и модификации дерева позволяет их упростить, благодаря подобной ссылке мы можем перемещаться по дереву не только в направлении от корня к нижележащим элементам, но и в обратном порядке.
Под LIST_OF_NODES подразумевается некий контейнер способный хранить внутри себя достаточное количество ссылок на поддеревья. В случае если количество не велико и относительно стабильно, то можно воспользоваться обычным массивом. В случае, когда количество элементом может варьироваться в произвольном диапазоне, то рекомендуется применять один из ранее изученных контейнеров: очередь, дек. Если вы используете средства STL, то можно объявить ссылку на множество поддеревьев так:
Алгоритмы формирования деревьев
До текущего момента все рассмотренные алгоритмы предполагали, что у нас есть построенное двоичное или мульти-дерево. Теперь мы рассмотрим схему формирования деревьев с упором именно на практические направления. Одним из важнейших направлений использования бинарных деревьев является оптимизация задач поиска. Когда мы рассматривали тему поиска, то из двух способов – линейных поиск (затраты порядка O(n)) и двоичного поиска (затраты порядка O(log n)) очевидным было применение именно второго подхода. Однако в этом случае нам было необходимо выполнить сортировку массива данных в противном случае алгоритм не работал. В случае использования двоичных деревьев можно создать такой алгоритм его формирования, что задача поиска в нем нужного элемента также будет составлять порядка O(log n).
Пример: предположим, что нашей программе на вход подается поток чисел (в общем случае не упорядоченный), если мы опишем узел дерева как
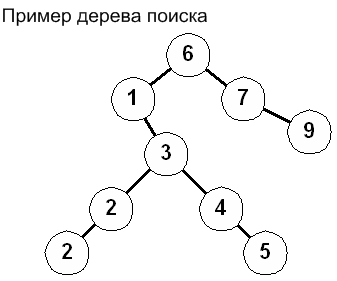
И потребуем чтобы все узлы, находящиеся в правом поддереве были больше чем корневой элемент, а все узлы из левого поддерева были не более чем корневой элемент, то в таком случае для последовательности чисел: 6 1 3 7 2 9 4 5 2 будет построено следующее дерево:
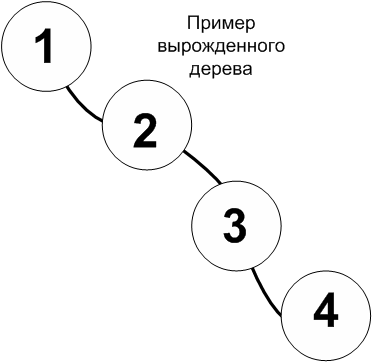
Деревья, для которых выполняется вышеописанное соотношение, называются деревьями поиска. В таком дереве, для того чтобы найти нужный элемент на каждом шаге пути необходимо принимать решение о выборе направления в зависимости от того, как соотносятся искомый элемент X и значение текущего узла Vi. Если Vi >= X то в таком случае поиск должен идти именно в левом поддереве, в противном случае в правом. Следует отметить, что получившееся двоичное дерево и соответственно эффективность операций поиска сильно зависит от степени упорядоченности поступающих наборов чисел. В случае если эти значения уже отсортированы, например: 1, 2, 3, 4 то получающееся дерево вырождается и начинает напоминать обычный линейный список.
В идеальном случае дерево должно быть сбалансированным. Напомню, что сбалансированным деревом является то, где количество узлов в правом и левом поддеревьях отличаются не более чем на 1. для повышения скорости работы алгоритма поиска в бинарном дереве также используют прием буфера (барьера). В этом случае все ветви будут заканчиваться не ссылкой на NULL, а ссылкой на этот буферный элемент. То, что у нас получилось можно увидеть на картинке:
Замечания к приведенным алгоритмам
В примере 2 предполагается наличие глобальной переменной GlobalBuffer, которая и является ссылкой на вспомогательный (фиктивный) барьерный элемент. Отметьте, что значение информационной компоненты data для этого буферного элемента перед началом цикла устанавливается в data, что позволяет упростить поиск за счет уменьшения количества операций сравнения. Часто начинающие программисты пытаются реализовать подобный поиск с помощью рекурсии, аргументируя, что раз структура данных рекурсивна то и поиск тоже должен быть таковым. Напоминаю, что настоятельно рекомендуется избегать применения рекурсии везде где это возможно из-за непроизводительных затрат на вызов функции.
Очевидно, что деревья будут вряд ли применяться в задачах, структуры данных которых сформированы и не изменяются на протяжении работы программы. Также очевидно, что на практике деревья должны будут расти и уменьшаться. Рассмотрим пример использования дерева для решения задачи частотного анализа.
Пример: предположим, что есть файл, содержащий некоторый объем текста. Для каждого из слов (как вариант, буквы) содержащегося в файле необходимо выполнить подсчет частоты его встречи. Простейшее решение, которое приходит в голову, это воспользоваться структурой данных типа ХЕШ (ассоциативный массив) в этом случае в качестве ключа будет использоваться само слово, в качестве его значения будет количество повторений. Разумеется, что хеш будет легко эмулировать с помощью двух массивов. В случае если файл содержит достаточно большое количество разных слов, то узким местом данного алгоритма будет поиск позиции, в которой встречается нужное слово. В случае если слова поступают в не отсортированном виде, что вполне ожидаемо, то мы должны будем просматривать в среднем половину от заполненного массива слов пока не найдем искомый. Можно воспользоваться, например, алгоритмом сортировки (здесь наиболее естественно применять метод вставки), мы же рассмотрим применение поискового дерева. Слова в нем будут располагаться в алфавитном порядке, т.е. все слова левого поддерева должны находиться в словаре раньше, чем корневой элемент, соответственно все слова правого поддерева должны находиться в словаре позже, чем корневой элемент (не забывайте, что такое соотношение должно выполняться для всех поддеревьев). Каждый раз, когда на вход программе будет поступать очередное слово будет выполняться поиск его схема идентична той, которая была приведена в таблице выше, если операция поиска была неудачна (функция из примера 1 вернула NULL, а функция из примера 2 вернула ссылку на сам буферный элемент), то необходимо в соответствующую позицию вставить новое слово, и его счетчик количества повторений инициализировать 1. После завершения формирования дерева его можно распечатать. Фрагмент кода решающего данную задачу приводится ниже.
В приведенном выше примере реализованы две версии функции для добавления нового слова в частотный словарь (нового узла в дерево) – одна из них не рекурсивная, вторая рекурсивна. Обратите внимание на то, каким именно образом в не рекурсивной версии обеспечивается модификация ссылки на узел (левой или правой) для родительского узла. В рекурсивной версии от использования двойной ссылки я отказался а, следовательно, был вынужден возвращать из функции ссылку на новое перестроенное дерево и присваивать его родительскому “left” или “right”.
Задание: в приведенном примере отсутствует код по удалению созданного дерева, освобождения занятой памяти. Добавьте его самостоятельно.
Подсказка: в терминах рекурсии операция удаления дерева формулируется практически идентично операции печати элементов. Что означает удалить дерево – сначала следует удалить левое поддерево, потом правое, и, наконец, сам корневой элемент. Когда вы это сделаете, то попробуйте найти также и не рекурсивное решение.
Задание: классической задачей также можно считать построения по заданному входному тексту дерева с перекрестными ссылками. Для каждого слова каждой строки текста необходимо определить информацию о том, в каких именно строках данное слово встречалось, а затем распечатать слова в алфавитном порядке с перечислением номеров строк. Подсказка в данном случае рекомендуется сочетать использование двоичного дерева из предыдущего примера, в каждом, из узлов которого будет храниться ссылка на другой вспомогательный контейнер для хранения номеров строк. Можно воспользоваться списком или деком из ранее рассмотренных тем. В случае если мы будем хранить именно номера строк, то можно пренебречь эффективностью решения задачи и применить фиксированный массив размером не более чем количество всех строк исходного текста. Однако более совершенным будет использование именно списка. Когда вы сделаете это задание, то попробуйте дальше развить пример и добавить необходимость работать с самими строками, а не их номерами, так можно создать глобальный массив с перечислением строк. А каждый элемент списка будет ссылкой на какой-нибудь из элементов массива строк.
Операции над деревьями. Проход дерева.
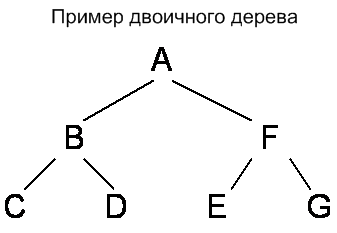
Методы обхода дерева будем рассматривать на примере двоичного дерева изображенного на следующем изображении (следует отметить, что выбор в качестве пример именно бинарного дерева ни коим образом не ограничивает общности наших рассуждений).
Проход дерева представляет собой систематическое посещение всех его узлов. Наиболее известна схема прямого и обратного прохода.
Прямой проход предполагает, что первое обращение осуществляется к корню дерева, а затем по очереди выполняется рекурсивный проход вдоль каждого из поддеревьев выходящих из корневого элемента. С использованием псевдокода эту операцию можно записать так:
Для приведенного нами выше дерева с буквами последовательность выводимых с помощью прямого прохода букв будет следующей:
Пример: Предположим, задано дерево арифметического выражения. Необходимо сформировать его строковое представление по следующему принципу:
Следовательно с помощью псевдокода алгоритм PrintForm(УзелДереваT) можно записать так:
В данном примере предполагается существование некоторого метода toString() который и печатает значение информационной компоненты каждого из узлов.
Обратный проход
Данный проход в некотором смысле является обратным к алгоритму прямого прохода. Прежде всего, идет посещение всех дочерних узлов и только потом корневого. Для приведенного нами выше дерева с буквами последовательность выводимых с помощью прямого прохода букв будет следующей:
Данный вид прохода применяется в том случае, когда необходимо сначала пройти дочерние элементы, например для подсчета некоторой характеристики и только потом на основании этой характеристики обработка узла.
Пример: рассмотрим задачу печати всех узлов дерева, которые имеют нечетное количество подчиненных узлов. В данном случае рекурсивный алгоритм BackPrintNodes (УзелДерева T) будет выглядеть так:
В приведенном фрагменте кода предполагается, что каждый узел дерева имеет ряд методов для доступа к поддеревьям.
Разумеется, что конкретный код реализации данных методов зависит от того какие именно задачи, какую предметную область представляет данное дерево. Однако обратите внимание на то, что сначала мы выполняем проход по всем поддеревьям накапливая количество всех подузлов которые есть у текущего элемента дерева.
В качестве еще одного пример обратного прохода можно привести определение в каком-либо из файловых менеджеров (far, windows commander, Norton commander) объема занимаемого некоторой директорией. Очевидно, что объем директории состоит из объема дискового пространства для хранения служебной информации непосредственно о директории, также объема занимаемого всеми файлами которые находятся в каталоге, и внимание, объема который занимают подкаталоги. Следовательно, мы снова вынуждены выполнить проход по всем подкаталогам (на всех уровнях вложенности) чтобы определить объем текущего каталога.
Иные способы прохода деревьев
Метод прямого и обратного прохода наиболее часто встречается, однако есть и иные способы, например проход по глубине.
Как вы уже знаете каждый узел дерева имеет глубину (расстояние между ним и корневым элементом). В методе прохода по глубине сначала выполняется проход по все узлам, имеющим глубину X, и только потом выполняется переход к узлам с глубиной X + 1.
Исключение элементов из дерева
Вспомогательная функция “helperDelete” выполняет спуск вдоль левого поддерева удаляемого элемента все время вправо до тех пор, пока не будет найден элемент, который не имеет правого, обозначим его как “R”, тогда выполняется копирования его значения в узел для удаляемого элемента, а на самом деле удаляется физически (освобождается память) именно элемент R. Если элемент R имеет левое поддерево, то для него выполняется код аналогичный общей схеме удаления для узла, имеющего одного потомка.
Задания по теме деревья
1) Пусть T – бинарное дерево с количеством узлов N. Предположим, что некоторый узел данного дерева V будет называться романским, если количество потомков в его левой ветви отличается от количества потомков правой ветви максимум на 5. Необходимо разработать метод с линейными затратами времени, который найдет все такие узлы дерева V* которые сами не являются романскими, но при этом все его потомки являются таковыми.
2) Необходимо разработать код приложения, который выполняет прямой проход по дереву, не использую методы рекурсии.
3) Длина пути дерева T вычисляется как сумма глубин всех узлов T. Необходимо разработать метод, который с линейными затратами времени найдет длину дерева T.
4) Напишите программу ввода и отображения генеалогического дерева в виде бинарного дерева. При выводе желательно придерживаться следующей схемы отображения, количество отступов перед выводом каждого имени должно быть равно глубине соответствующего узла:
5) Реализуйте бинарное дерево, используя двунаправленную очередь (подсказка: это задание является развитием способа представления дерева в виде массива, но при этом мы не храним пустые (неиспользуемые элементы дерева). Можно использовать в качестве узла дерева структуру из двух полей: информация об узле а также его порядковый номер).
Разделы
Copyright © Study & Dev | Powered by WordPress