Что такое высказывание в математике примеры

Высказывание (логика)

Высказывательной формой называется логическое высказывание, в котором один из объектов заменён переменной. При подстановке вместо переменной какого-либо значения высказывательная форма превращается в высказывание. Пример: A(x) = «В городе x идёт дождь.», где A — высказывательная форма, x — объект.

Содержание

Виды высказываний

Логические высказывания принято подразделять на два вида: элементарные логические высказывания и составные логические высказывания.

Составное логическое высказывание — это высказывание, образованное из других высказываний с помощью логических связок.

Элементарные логические высказывания — это высказывания не относящиеся к составным.

Примеры: «Петров — врач», «Петров — шахматист» — элементарные логические высказывания. «Петров — врач и шахматист» — составное логическое высказывание, состоящие из двух элементарных высказываний, связанных между собой при помощи связки «и».

Связь с математической логикой

Обычная логика двухзначна, то есть приписывает высказываниям только два возможных значения: истинно оно или ложно.

Пусть — высказывание. Если оно истинно, то пишут , если ложно, то .

Тождественно истинное высказывание обозначают символом 1, тождественно ложное — символом 0.

Основные операции над логическими высказываниями

Отрицание логического высказывания — логическое высказывание, принимающее значение «истинно», если исходное высказывание ложно, и наоборот.

Конъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны.

Дизъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно.

Импликация двух логических высказываний A и B — логическое высказывание, ложное только тогда, когда B ложно, а A истинно.

Равносильность (эквивалентность) двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны.

Кванторное логическое высказывание с квантором всеобщности () — логическое высказывание, истинное только тогда, когда для каждого объекта x из заданной совокупности высказывание A(x) истинно.

Кванторное логическое высказывание с квантором существования () — логическое высказывание, истинное только тогда, когда в заданной совокупности существует объект x, такой, что высказывание A(x) истинно.

См. также

Примечания

Литература

Полезное

Смотреть что такое «Высказывание (логика)» в других словарях:

Высказывание — Высказывание: Высказывание (логика) предложение, которое может быть истинно или ложно. Высказывание (лингвистика) предложение в конкретной речевой ситуации. См. также Суждение … Википедия

ЛОГИКА — (от греч. logos слово, понятие, рассуждение, разум), или Формальная логика, наука о законах и операциях правильного мышления. Согласно основному принципу Л., правильность рассуждения (вывода) определяется только его логической формой, или… … Философская энциклопедия

ЛОГИКА ВЫСКАЗЫВАНИЙ — раздел логики, в котором изучаются истинностные взаимосвязи между высказываниями. В рамках данного раздела высказывания (пропозиции, предложения) рассматриваются только с т.зр. их истинности или ложности, безотносительно к их внутренней субъектно … Философская энциклопедия

логика высказываний — ЛОГИКА ВЫСКАЗЫВАНИЙ, пропозициональная логика раздел символической логики, изучающий сложные высказывания, образованные из простых, и их взаимоотношения. В отличие от логики предикатов, простые высказывания при этом выступают как… … Энциклопедия эпистемологии и философии науки

ВЫСКАЗЫВАНИЕ — грамматически правильное повествовательное предложение, взятое вместе с выражаемым им смыслом. В логике употребляется несколько понятий В., существенно различающихся между собой. Прежде всего это понятие дескриптивного, или о п и с а тельного,… … Философская энциклопедия

Логика Бэрроуза — Логика Бэрроуза Абади Нидхэма (англ. Burrows Abadi Needham logic) или BAN логика (англ. BAN logic) это формальная логическая модель для анализа знания и доверия, широко используемая при анализе протоколов… … Википедия

ЛОГИКА ПРЕДИКАТОВ — центральный раздел логики, в котором изучается субъектно предикатная структура высказывании и истинностные взаимосвязи между ними. Л.п. представляет собой содержательное расширение логики высказываний. В рамках данного раздела любое высказывание… … Философская энциклопедия

ЛОГИКА НАУЧНОГО ПОЗНАНИЯ — или Логика науки, применение идей, методов и аппарата логики в анализе научного познания. Развитие логики всегда было тесно связано с практикой теоретического мышления и прежде всего с развитием науки. Конкретные рассуждения дают логике материал … Философская энциклопедия

ЛОГИКА СИМВОЛИЧЕСКАЯ — ЛОГИКА СИМВОЛИЧЕСКАЯ математическая логика. теоретическая логика область логики, в которой логические выводы исследуются посредством логических исчислений на основе строгого символического языка. Термин “символическая логика” был, по видимому … Философская энциклопедия

ЛОГИКА НАУКИ — в спец. смысле дисциплина, применяющая понятия и технич. аппарат совр. формальной логики к анализу систем науч. знания. Термин «Л. н.» часто употребляется также для обозначения законов развития науки (логика науч. развития), правил и… … Философская энциклопедия

Источник

Математические понятия, предложения и доказательства

Юлия Мехонцева
Математические понятия, предложения и доказательства

МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ, ПРЕДЛОЖЕНИЯ И ДОКАЗАТЕЛЬСТВА

1.,2. Понятий в начальном курсе математики изучается много. Как же их определяют?

Неявные определения: контекстуальные и остенсивные.

В контекстуальных определениях содержание нового понятия раскрывается через отрывок текста, через контекст, через анализ конкретной ситуации.

Пример – определение уравнения в традиционном курсе математики: равенство, содержащее букву (буквы, значение которой (которых) надо найти.

Остенсивные определения – это определения путем показа. Они используются для введения терминов путем демонстрации объектов, которые этими терминами обозначают.

Например, таким образом вводятся понятия равенства и неравенства в начальном курсе математики.

Каждое понятие объединяет в себе класс объектов (вещей, отношений). Это объем понятия и характеристическое свойство присуще всем объектам этого класса только им.

Например, понятие треугольник содержит в себе класс всевозможных треугольников, это объем понятия и характеристические свойства, наличие трех сторон, трех вершин, трех углов – содержание понятия.

Например, прямоугольником называется параллелограмм с прямыми углами. Прямоугольник определяемое понятие, параллелограмм ближайший род – определяющее понятие. Прямой угол видовое отличие.

5. Высказывания и высказывательные формы

Относительно понятий и отношений между ними можно высказывать различные суждения. Языковой формой суждений являются повествовательные предложения. Например, в начальном курсе математики можно встретить такие предложения:

1) число 12 – четное;

4) В числе 15 один десяток и 5 единиц;

5) От перестановки множителей произведение не изменяется;

6) Некоторые числа делятся на 3.

Видим, что предложения, используя в математике, могут быть записаны как на естественном (русском) языке, так и на математическом, с использованием символов. Далее, о предложениях 1, 4, 5 и 6 можно сказать, что они несут верную информацию, а предложение 2 – ложную. Относительно предложения х + 5 =8 вообще нельзя сказать: истинное оно или ложное. Взгляд на предложение с позиции – истину или ложь оно нам сообщает – привел к понятию высказывания.

Определение. Высказыванием в математике называют предложение,относительно которого имеет смысл вопрос: истинно оно или ложно.

Например, предложения 1, 2, 4, 5 и 6 – высказывания, причем предложения 1, 4, 5 и 6 – истинные, а 2 – ложное.

Высказывания принято обозначать прописными буквами латинского алфавита: А, В, С,, Z. Если высказывание А истинно,то записывают: А – «и», если же высказывание А – ложно,то пишут: А – «л».

«Истина» и «ложь» называются значениями истинности высказывания. Каждое высказывание либо истинно, либо ложно, быть одновременно тем и другим оно не может.

Предложение х + 5 = 8 не является высказыванием,так как о нем нельзя сказать: истинно оно или ложно.Однако при подстановке конкретных значений переменной х оно обращается в высказывание: истинное или ложное. Предложение х + 5 = 8 называется высказывательной формой. Оно порождает множество высказываний одной и той же формы.

Среди всех возможных значений переменной нас в первую очередь интересуют те, которые обращают высказывательную форму в истинное высказывание. Множество таких значений переменных называют множеством истинности высказывательной формы.

Например, множеством истинности высказывательной формы х > 5, заданной на множестве действительных чисел, будет промежуток (5;). Множество истинности высказывательной формы х + 5 = 8, заданной на множестве целых неотрицательных чисел, состоит из одного числа 3.

4. Предложения, которые мы рассматривали, были простыми, но можно привести примеры суждений, языковой формой которых будут сложные предложения.

Например: «Если треугольник равнобедренный, то углы при основании в нем равны».

В логике считают, что из двух данных предложений можно образовать новые предложения, используя для этого союзы «и», «или», «если…, то», «тогда и только тогда, когда», а также частица «не» или словосочетание «неверно, что». Слова «и», «или», «если, то», «тогда и только тогда, когда», а также частица «не» называют логическими связками. Предложения, образованные из других предложений с помощью логических связок, называют составными. Предложения, не являющиеся составными, называют элементарными.

Приведем примеры составных предложений.

1) Число 28 четное и делится на 7.

2) Число х меньше или равно 8.

3) Число 14 не делится на 4.

Эти предложения, являясь с логической точки зрения составными, по своей грамматической структуре – простые.

Как определить значение истинности составного высказывания, например, «число 28 делится на 7 и на 9»? Значение истинности высказываний определяется с помощью определенных правил. Но для этого нужно уметь выявлять логическую структуру высказывания.

1) из каких элементарных предложений образовано данное составное предложение;

2) с помощью каких логических связок оно образовано.

Используя данное определение, найдем значение истинности высказывания «число 28 делится на 7 и на 9», которое, как было установлено раньше, состоит из двух элементарных высказываний, соединенных союзом «и», т. е. является конъюнкцией. Так как первое высказывание истинно, а второе ложно, то, согласно определению конъюнкции, высказывание «число 28 делится на 7 и на 9» будет ложным.

Конспект занятия по формированию общего понятия о военных профессиях в старшей группе Задачи. 1. Расширить представление детей о разнообразии профессий. 2. Формировать обобщенное понятие «профессия военных», обогащать активный.

Характеристика понятия «творческие способности детей» (первая часть) По утверждению педагогов-исследователей (Н. А. Ветлугиной, Т. С. Комаровой, В. С. Кузина, Б. М. Неменского, Н. П. Сакулиной, В. А. Флериной и.

Характеристика понятия «творческие способности детей» (вторая часть) 13. Легкость генерирования идей. Чем больше идей порождает человек, тем больше шансов, что среди них будут идеи хорошие. 14. Беглость речи.

Конспект НОД по ФЭМП в старшей группе для детей с ОВЗ «Понятия внутри-снаружи» Автор: учитель-дефектолог, логопед Скрябина Светлана Николаевна МКДОУ №133 г. Кирова Цель: формирование у детей навыков ориентировки в.

Конспект образовательного предложения на тему «В помощь дедушке Фольклору» (средняя группа) Цель: Приобщение детей к истокам русского народного фольклора через сказку. Задачи: • Пополнять и закреплять знания детей об устном народном.

Конспект урока русского языка «Предложения с прямой речью» (4 класс) РУССКИЙ ЯЗЫК ПРЕДЛОЖЕНИЯ С ПРЯМОЙ РЕЧЬЮ Тема: Знаки препинания в предложении с прямой речью, когда прямая речь стоит перед словами автора.

Консультация для родителей «Формирование структуры предложения у детей пяти лет» Цель: Знакомство родителей с формированием структуры предложения у детей пяти лет. Задачи: 1. Познакомить родителей с формированием структуры.

Логико-математические понятия в повседневной жизни В группе Какой карандаш длиннее, короче? Как проверить? Что можно сказать о длине трех ленточек? Как проверить? Какая пирамидка выше, ниже?.

Словесные упражнения, направленные на формирование структуры предложения Согласование подлежащего с прилагательным (определением) Воспитатель: Правильно ли я говорю: Малыш веселый? С какими словами можно еще связать.

Источник

Знания за пределами математики и доказательной логики состоят из предположений. Предположения, составляющие математические знания, закрепляются доказательными рассуждениями и подкрепляются правдоподобными рассуждениями. Математическое доказательство является доказательным рассуждением, косвенные улики юриста, индуктивные доводы физика, статистические доводы экономиста относятся к правдоподобным рассуждениям. Доказательное рассуждение надежно, неоспоримо, окончательно. Правдоподобное рассуждение рискованно, спорно, условно.

Доказательное рассуждение имеет жесткие стандарты, кодифицированные и выясненные логикой, являющейся теорией доказательных рассуждений. Стандарты правдоподобных рассуждений текучи и нет никакой теории таких рассуждений, которая могла бы сравниться с доказательной логикой или обладала бы сравнимой с ней согласованностью.

Доказательные рассуждения. Все новые знания о мире связаны с правдоподобными рассуждениями.

Часто математические утверждения касаются бесконечного множества объектов, и перебрать эти объекты невозможно. Такой перебор можно заменить следующим методом рассуждения: если данное утверждение истинно в одном случае, то оно окажется истинным и в следующем за ним случае, а значит и во всех случаях. Такой метод рассуждения называется методом математической индукции.

Обобщение есть переход от рассмотрения данного множества предметов к рассмотрению большего множества, содержащего данное. Обобщение часто делается при переходе от одного предмета к целому классу, содержащему этот предмет.

Специализация есть переход от рассмотрения данного множества предметов к рассмотрению меньшего множества, содержащегося в данном. Специализация часто производится при переходе от целого класса предметов к одному предмету, содержащемуся в этом классе.

Аналогия. Две системы аналогичны, если они согласуются в ясно определенных отношениях соответствующих частей. Это отношение имеет ясный смысл, если отношения управляются одними и теми же законами.

Далее приводятся некоторые основные факты математической логики, которую еще называют формальной логикой. Формальной потому, что она позволяет проверить правильность рассуждений независимо от их содержания. Цепочки рассуждений в совершенно разных областях математики и других наук можно одинаково описать на языке логики и убедиться в их справедливости или ошибочности.

Высказывания и логические связки

Многие математические понятия удобно записывать в виде выражений, содержащих некоторые логические символы. Так, символ V, называемый квантором общности, используется вместо слов: «для любого», «для всех», «каково бы ни было. » и т.д., а символ

Отрицание — это высказывание, которое получается из данного высказывания А с помощью слова «не». Отрицание можно обозначать по-разному: .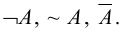

Простое добавление слова «не» к высказыванию чаще всего будет противоречить языковым нормам. Поэтому в конкретных случаях

требуется «перевод» полученного высказывания на русский язык. Пусть, например, А = «Завтра пойдет дождь». Что значит «Не (Завтра пойдет дождь)»: «Дождь пойдет не завтра», «Завтра пойдет не дождь» или «Завтра не пойдет дождь»? Здравый смысл подсказывает, что отрицанием высказывания А является третье предложение. Чтобы определить точно, дадим формальное определение отрицания.

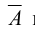
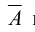
Отрицанием высказывания А называется такое высказывание, которое принимает значение / (ложно), если высказывание А истинно, и значение t (истинно), если высказывание А ложно. В нашем примере этому условию удовлетворяет только третье предложение. Итак, = «Завтра не пойдет дождь».

Дизъюнкция строится с помощью неисключающего «или». Таким образом, дизъюнкция A v В истинна, когда истинно, по крайней мере, одно из высказываний А и В или оба вместе. Другими словами, дизъюнкция ложна в том и только в том случае, когда оба высказывания ложны.

Импликация образуется из высказываний А и В с помощью слов «если. то. ». Получается высказывание вида «если А то В». Напомним, что математическая логика носит формальный характер, содержанием высказываний она не, занимается.

На примере импликации хорошо видна разница между обычным языком и языком логики. В обычном языке сложное предложение «если А, то В» предполагает между А и В отношение посылки и следствия, или же причины и обусловленного ею действия.

Импликация обозначается 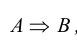, при этом говорят: «А влечет В» или «В при условии, что А», «В, если А», «А есть достаточное условие для В», «В есть необходимое условие для А».

Договорились, что импликация 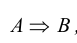ложна в том и только в том случае, когда высказывание А истинно, а высказывание В ложно. Такое определение подсказано здравым смыслом: разумно считать импликацию истинной, если В истинно, независимо от значения А; если оба участника импликации ложны, импликация, естественно, также истинна. В единственном случае, когда «предпосылка» импликации истинна, а «вывод» ложен, импликация считается ложной.

Эквиваленция образуется из высказываний А и В с помощью слов «. тогда и только тогда, когда. »:

Утверждение «А тогда и только тогда, когда В» не означает в логике, что составляющие высказывания А и В имеют одно и то же значение или один и тот же смысл.

Эквиваленция обозначается , Синонимы для эквиваленции: «если А, то В, и если В, то А», «А в том и только в том случае, когда «И есть необходимое и достаточное условие для В», «В есть необходимое и достаточное условие для А». Разумное определение эквиваленции: эквиваленция истинна в том и только в том случае, когда высказывания А и В имеют одинаковое значение истинности (либо оба истинны, либо оба ложны).

Новые высказывания (отрицание, дизъюнкция, конъюнкция, импликация и эквиваленция) образуются из существующих высказываний с помощью операций, или логических связок, имеющих те же названия.

В логике, как и в арифметике, операции делятся по старшинству. Это позволяет при записи сложных высказываний избегать большого количества скобок. Порядок выполнения операций таков: приоритет имеет отрицание, затем на одном уровне — дизъюнкция и конъюнкция, следующая связка — импликация и, наконец, самая последняя — эквиваленция.

Лекции по предметам:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Что такое высказывание в математике примеры

Тема 3. Основы математической логики 1. Логические выражения и логические операции.
2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

1. Логические выражения и логические операции

Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).

Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.

Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.

Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.

Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.

С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.

Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.

В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.

Существуют разные варианты обозначения истинности и ложности логических переменных:

Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).

Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.

Введем перечисленные логические операции.

В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.

Источник