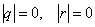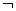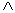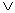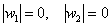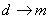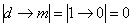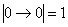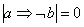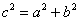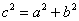Что такое высказывание в дискретной математике

Основы дискретной математики

Привет, хабр. В преддверии старта базового курса «Математика для Data Science» делимся с вами переводом еще одного полезного материала.

Об этой статье

Эта статья содержит лишь малую часть информации по заявленной теме. Рассматривайте ее как вводный курс перед началом всестороннего изучения предмета. Надеюсь, вы найдете в ней полезную информацию. Знание дискретной математики помогает описывать объекты и задачи в информатике, особенно когда дело касается алгоритмов, языков программирования, баз данных и криптографии. В дальнейшем я планирую подробнее раскрыть темы, затронутые в этой статье. Приятного чтения!

ЧТО ТАКОЕ ДИСКРЕТНАЯ МАТЕМАТИКА?

Это область математики, изучающая объекты, которые могут принимать только уникальные отдельные значения.

Мы рассмотрим пять основных разделов в следующем порядке.

ЛОГИКА

Что такое логика?

Это наука о корректных рассуждениях. Мы будем использовать приемы идеализации и формализации. Неформальная логика изучает использование аргументов в естественном языке.

Формальная логика анализирует выводы с чисто формальным содержанием. Примерами формальной логики являются символическая логика и силлогистическая логика (о которой писал Аристотель).

Начнем с азов. Рассмотрим следующее высказывание на естественном языке:

«Если я голоден, я ем».

Пусть «голоден» будет посылкой A, а «ем» — следствием B. Попробуем формализовать:

A => B (то есть из A следует B)

NB. Посылка и следствие являются суждениями.

Логические выражения

Для нас важна форма, а НЕ содержание. Значение будет истинным, если оно соответствует форме.

Например, 10 4 — ИСТИНА.

Логические операции

Суждение P — это утверждение, которое может быть как истинным, так и ложным.

Обозначим истинное значение P единицей (1), а ложное значение P нулем (0).

Существует другое суждение; обозначим истинное значение Q единицей (1), а ложное значение Q нулем (0).

Рассмотрим логические операции с суждениями, значение которых истинно. Они могут сами образовывать истинные значения путем выполнения соответствующих операций над истинными значениями.

Источник

Дискретная математика — логика высказываний

Правила математической логики определяют методы обоснования математических утверждений. Греческий философ Аристотель был пионером логических рассуждений. Логические рассуждения обеспечивают теоретическую основу для многих областей математики и, следовательно, информатики. Он имеет множество практических приложений в области компьютерных наук, таких как проектирование вычислительных машин, искусственный интеллект, определение структур данных для языков программирования и т. Д.

Логика высказываний связана с утверждениями, которым могут быть присвоены значения истинности «истина» и «ложь». Цель состоит в том, чтобы проанализировать эти утверждения по отдельности или в совокупности.

Предлогическая логика — определение

Предложение — это совокупность декларативных утверждений, которые имеют либо значение истины «истина», либо значение истины «ложь». Пропозициональное предложение состоит из пропозициональных переменных и связок. Мы обозначаем пропозициональные переменные заглавными буквами (A, B и т. Д.). Связки соединяют пропозициональные переменные.

Некоторые примеры предложений приведены ниже —

Следующее не является предложением —

«А меньше 2». Это потому, что если мы не дадим конкретное значение A, мы не сможем сказать, является ли утверждение истинным или ложным.

«А меньше 2». Это потому, что если мы не дадим конкретное значение A, мы не сможем сказать, является ли утверждение истинным или ложным.

Связки

В логике высказываний мы обычно используем пять связок, которые:

Отрицание / НЕ ( l n o t )

Импликация / если-тогда ( r i g h t a r r o w )

Если и только если ( L e f t r i g h t a r r o w ).

Отрицание / НЕ ( l n o t )

Импликация / если-тогда ( r i g h t a r r o w )

Если и только если ( L e f t r i g h t a r r o w ).

OR ( l o r ) — Операция OR двух предложений A и B (записанная как A l o r B ) выполняется, если хотя бы любая из пропозициональных переменных A или B истинна.

Таблица истинности выглядит следующим образом —

AND ( l a n d ) — Операция AND двух предложений A и B (записанная как A l a n d B ) верна, если обе пропозициональные переменные A и B верны.

Таблица истинности выглядит следующим образом —

Отрицание ( l n o t ) — отрицание предложения A (записанного как l n o t A ) ложно, когда A истинно, и истинно, когда A ложно.

Таблица истинности выглядит следующим образом —

Импликация / если-тогда ( r i g h t a r r o w ) — импликация A r i g h t a r r o w B — это предложение «если A, то B». Это ложно, если A верно, а B ложно. Остальные случаи верны.

Таблица истинности выглядит следующим образом —

Если и только если ( L e f t r i g h t a r r o w ) — A L e f t r i g h t a r r o w B — это двухусловное логическое связующее, которое истинно, когда p и q одинаковы, т.е. оба являются ложными или оба истинны.

Таблица истинности выглядит следующим образом —

Тавтологии

Тавтология — это формула, которая всегда верна для каждого значения ее пропозициональных переменных.

Пример — Доказать, что l b r a c k ( A r i g h t a r r o w B ) l a n d A r b r a c k r i g h t a r r o w B — тавтология

Таблица истинности выглядит следующим образом —

Как мы видим, каждое значение l b r a c k ( A r i g h t a r r o w B ) l a n d A r b r a c k r i g h t a r r o w B равно «True», это тавтология.

Противоречия

Противоречие — это формула, которая всегда ложна для каждого значения ее пропозициональных переменных.

Пример — Докажите, что ( A l o r B ) l a n d l b r a c k ( l n o t A ) l a n d ( l n o t B ) r b r a c k является противоречием

Таблица истинности выглядит следующим образом —

Как мы видим, каждое значение ( A l o r B ) l a n d l b r a c k ( l n o t A ) l a n d ( l n o t B ) r b r a c k равно «False», это противоречие.

непредвиденные обстоятельства

Непредвиденные обстоятельства — это формула, которая имеет как истинные, так и ложные значения для каждого значения своих пропозициональных переменных.

Пример — Доказать непредвиденную случайность в ( A l o r B ) l a n d ( l n o t A )

Таблица истинности выглядит следующим образом —

Как мы видим, каждое значение ( A l o r B ) l a n d ( l n o t A ) имеет «True» и «False», это непредвиденное обстоятельство.

Пропозициональные эквивалентности

Два утверждения X и Y логически эквивалентны, если выполняется любое из следующих двух условий:

Таблицы истинности каждого утверждения имеют одинаковые значения истинности.

Двухусловное утверждение X L e f t r i g h t a r r o w Y является тавтологией.

Таблицы истинности каждого утверждения имеют одинаковые значения истинности.

Двухусловное утверждение X L e f t r i g h t a r r o w Y является тавтологией.

Пример — Докажите, что l n o t ( A l o r B ) и l b r a c k ( l n o t A ) l a n d ( l n o t B ) r b r a c k эквивалентны

Тестирование по 1- му методу (таблица соответствия)

Здесь мы видим, что значения истинности l n o t ( A l o r B ) и l b r a c k ( l n o t A ) l a n d ( l n o t B ) r b r a c k совпадают, поэтому утверждения эквивалентны.

Тестирование по 2- му методу (би-условность)

Поскольку l b r a c k l n o t ( A l o r B ) r b r a c k L e f t r i g h t a r r o w l b r a c k ( l n o t A ) l a n d ( l n o t B ) r b r a c k является тавтологией, утверждения эквивалентны.

Обратное, Обратное и Противоположительное

Импликация / if-then ( r i g h t a r r o w ) также называется условным оператором. Он состоит из двух частей —

Пример условного высказывания — «Если вы делаете свою домашнюю работу, вы не будете наказаны». Здесь «вы делаете свою домашнюю работу» — это гипотеза, p, а «вы не будете наказаны» — это заключение, q.

Пример — Противоположный вариант «Если вы делаете домашнее задание, вы не будете наказаны» — «Если вы наказаны, вы не сделали домашнее задание».

Принцип двойственности

Принцип двойственности гласит, что для любого истинного утверждения двойственное утверждение, полученное путем взаимного объединения союзов в пересечения (и наоборот) и взаимного изменения универсального множества в нулевое множество (и наоборот), также верно. Если дуальным каким-либо утверждением является само утверждение, оно называется самодвойственным утверждением.

Пример — двойственное значение ( A c a p B ) c u p C равно ( A c u p B ) c a p C

Нормальные Формы

Мы можем преобразовать любое предложение в две нормальные формы —

Конъюнктивная нормальная форма

Составной оператор находится в конъюнктивной нормальной форме, если он получен путем операции И среди переменных (включая отрицание переменных), связанных с ИЛИ. С точки зрения операций над множествами, это составное утверждение, полученное Intersection среди переменных, связанных с Unions.

( A l o r B ) з е м л я ( A l o r C ) з е м л я ( B l o r C l o r D )

( P c u p Q ) c a p ( Q c u p R )

( A l o r B ) з е м л я ( A l o r C ) з е м л я ( B l o r C l o r D )

( P c u p Q ) c a p ( Q c u p R )

Дизъюнктивная нормальная форма

Составной оператор находится в конъюнктивной нормальной форме, если он получен путем операции ИЛИ среди переменных (включая отрицание переменных), связанных с AND. С точки зрения операций над множествами, это составное утверждение, полученное объединением среди переменных, связанных с пересечениями.

( A l a n d B ) l o r ( A l a n d C ) l o r ( B l a n d C l a n d D )

Источник

Основы математической логики

Второй урок практического курса высшей алгебры будет посвящён основам математической логики, которая представляет собой не только отдельный раздел математики, но и имеет огромное значение при изучении всей вышки (да и не только вышки). «Существует и единственно», «из этого следует это», «необходимое условие», «достаточность», «тогда и только тогда» – знакомые обороты, не правда ли? И это не просто «дежурные» штампы, которыми можно пренебречь – это устойчивые выражения, обладающие строгим смыслом, с которым мы и познакомимся в данной статье. Кроме того, материал будет полезен начинающим изучать непосредственно математическую логику – я рассмотрю её базу: высказывания и действия над ними, формулы, основные законы + некоторые практические задачи. И, конечно же, вы узнаете очень важное, а местами и весьма забавное отличие матлогики от нашей «обычной» логики. Начинаем закладывать фундамент:

Высказывания и высказывательные формы

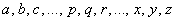
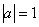
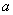
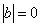
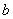
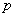
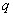
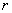
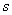
Высказывание – это предложение, о котором можно сказать, истинно оно или ложно. Высказывания обычно обозначают строчными латинскими буквами , а их истинность/ложность единицей и нулём соответственно:

– данная запись (не путать с модулем!) говорит нам о том, что высказывание истинно;
– а эта запись – о том, что высказывание ложно.

– черепахи не летают;
– Луна квадратная;
– дважды два будет два;
– пять больше, чем три.

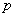
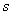
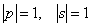
Совершенно понятно, что высказывания и истинны: ,
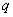
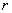
а высказывания и – ложны:

Разумеется, далеко не все предложения являются высказываниями. К таковым, в частности относятся вопросительные и побудительные предложения:

Вы не подскажете, как пройти в библиотеку?
Пойдём в баню!

Очевидно, что здесь не идёт речи об истине или лжи. Как не идёт о них речи и в случае неопределённости либо неполной информации:

Завтра Петя сдаст экзамен – даже если он всё выучил, то не факт, что сдаст; и наоборот – если ничего не знает, то может и сдаст «на шару».

…да ладно, Петь, не переживай – сдашь =)

– а тут мы не знаем, чему равно «эн», поэтому это тоже не высказывание.

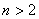
Однако последнее предложение можно доопределить до высказывания, а точнее, до высказывательной формы, указав дополнительную информацию об «эн». Как правило, высказывательные формы записываются с так называемыми кванторами. Их два:

– квантор общности (перевёрнутая буква A – от англ. All) понимается и читается как «для всех», «для любого (ой) (ых) »;

– квантор существования (развёрнутая буква E – от англ. Exist) понимается и читается как «существует».

– для любого натурального числа выполнено неравенство . Данная высказывательная форма ложна, поскольку ей, очевидно, не соответствуют натуральные числа .

– а вот это высказывательная форма уже истинна, как истинно и, например, такое утверждение:
…ну а что, разве существует натуральное число, которое меньше, чем –10?

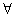
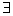
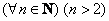
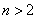
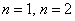
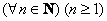
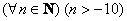
Предостерегаю вас от опрометчивого использования данного квантора, ибо «для любого» может на поверку оказаться вовсе и «не для любого».

Внимание! Если вам что-то не понятно в обозначениях, пожалуйста, вернитесь к уроку о множествах.

– существует натуральное число, которое больше двух. Истина …и, главное, не поспоришь =)

– Ложь

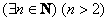
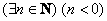
Нередко кванторы «работают в одной упряжке»:

– для любого вектора существует противоположный ему вектор. Прописная истина, а точнее, аксиома (утверждение, принимаемое без доказательства) векторного пространства.

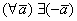
Обратите внимание, что квантор существования подразумевает сам факт существования объекта (хотя бы одного), который удовлетворяет определённым характеристикам. Пусть в мире существуют единственная белая ворона, но существуют же. Более того, в математике (как школьной, так и высшей) доказывается великое множество теорем на существование и как раз единственность чего-либо. Доказательство такой теоремы состоит из двух частей:

1) Существование объекта, удовлетворяющего определённым критериям. В этой части обосновывается сам факт его существования.

2) Единственность данного объекта. Этот пункт доказывается, как правило, методом от противного, т.е. предполагается, что существует 2-й объект с точно такими же характеристиками и далее это предположение опровергается.

Школьников, впрочем, стараются не пугать подобной терминологией, и теорема часто преподносится в завуалированном виде, например:

В любой треугольник можно вписать окружность и, причём только одну

Кстати, а что такое вообще теорема? Логическую суть этого страшного слова мы узнаем очень скоро….

Логические операции (действия над высказываниями)

Подобно тому, как с числами можно проводить арифметические действия (складывать, умножать и т.д.), к высказываниям тоже применимы свои операции. Существует три базовых логических операции:

отрицание высказывания;

конъюнкция или логическое умножение высказываний;

дизъюнкция или логическое сложение высказываний.

1) Отрицание высказывания

Данной операции соответствует логическая связка НЕ и символ

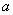
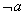
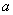
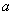
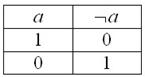
Отрицанием высказывания называется высказывание (читается «не а»), которое ложно, если истинно, и истинно – если ложно:

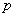
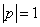
Так, например, высказывание – черепахи не летают истинно: ,
а его отрицание 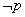– черепахи летают если хорошенько пнуть – ложно: ;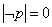

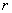
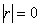
высказывание – дважды два будет два ложно: ,
а его отрицание 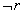– неверно, что дважды два будет два – истинно: .

Кстати, не нужно смеяться над примером с черепахами 😉 садисты

Удачной физической моделью данной операции является обычная лампочка и выключатель:

свет включен – логическая единица или истина,
свет выключили – логический ноль или ложь.

2) Конъюнкция (логическое умножение высказываний)

Данной операции соответствует логическая связка И и символ 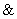либо

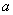
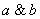
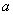
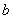
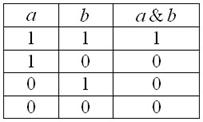
Конъюнкцией высказываний и называют высказывание (читается «а и бэ»), которое истинно в том и только том случае, когда истинны оба высказывания и :

Данная операция тоже встречается сплошь и рядом. Вернёмся к нашему герою с первой парты: предположим, что Петя получает допуск к экзамену по высшей математике, если сдаёт курсовую работу и зачёт по теме. Рассмотрим следующие высказывания:
– Петя сдал курсовую работу;
– Петя сдал зачёт.

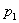
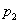
Заметьте, что в отличие от формулировки «Петя завтра сдаст» здесь уже в любой момент времени можно сказать, истина это или ложь.

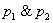
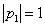
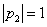
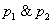
Высказывание (суть – Петя допущен к экзамену) будет истинно в том и только том случае, если он сдал курсовик и зачёт по . Если хоть что-то не сдано (см. три нижних строчки таблицы), то конъюнкция – ложна.

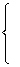
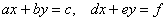
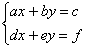
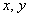
И очень своевременно пришёл мне в голову отличный математический пример: знак системы соединяет входящие в неё уравнения/неравенства как раз по правилу И. Так, например, запись двух линейных уравнений в систему подразумевает то, что мы должны найти ТАКИЕ корни (если они существуют), которые удовлетворяют и первому и второму уравнению.

Рассматриваемая логическая операция распространяется и на большее количество высказываний. Условно говоря, если в системе 5 уравнений, то её корни (в случае их существования) должны удовлетворять и 1-му и 2-му и 3-му и 4-му и 5-му уравнению данной системы.

И в заключение пункта вновь обратимся к доморощенной электротехнике: конъюнктивное правило хорошо моделирует выключатель в комнате и рубильник на электрическом щитке в подъезде (последовательное подключение). Рассмотрим высказывания:

– выключатель в комнате включен;

– рубильник в подъезде включен.

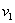
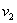
Наверное, все уже поняли, что конъюнкция читается самым что ни на есть естественным образом:
– выключатель в комнате включен и рубильник в подъезде включен.

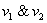
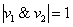
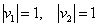
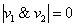
Очевидно, что тогда и только тогда, когда . В трёх других случаях (проанализируйте, каких) цепь разомкнётся и свет погаснет: .

Давайте присоединим ещё одно высказывание:
– рубильник на подстанции включен.

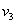
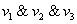
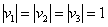
Аналогично: конъюнкция будет истинна тогда и только тогда, когда . Здесь, к слову, уже будет 7 различных вариантов разрыва цепи.

3) Дизъюнкция (логическое сложение высказываний)

Этой операции соответствует логическая связка ИЛИ и символ

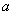
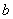
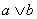
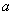
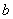
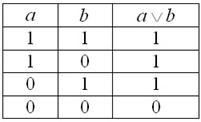
Дизъюнкцией высказываний и называют высказывание (читается «а или бэ»), которое ложно в том и только том случае, когда ложны оба высказывания и :

Предположим, что в экзаменационном билете по высшей математике 2 вопроса и студент сдаёт экзамен, если ответит хотя бы на один вопрос. Рассмотрим следующие высказывания:
– Петя ответил на 1-й вопрос;
– Петя ответил на 2-й вопрос.

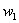
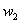
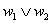
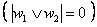
Дизъюнктивная запись читается просто и понятно: Петя ответил на 1-й или 2-й вопрос и подразумевает три истинных исхода (см. таблицу). При этом экзамен Пётр не сдаст в единственном случае – если «запорет» оба вопроса:

Следует отметить, что союз «или» мы очень часто понимаем как «исключающее или», и, более того – его зачастую так и нужно понимать! Из той же фразы о сдаче экзамена человек, скорее всего, сделает вывод, что Петя ответил только на 1-й или только на 2-й вопрос. Однако рассматриваемое ИЛИ – это не обывательское «или».

Операция логического сложения также применима для трёх и бОльшего количества высказываний. Некоторые лояльные преподаватели задают 10-15 вопросов и ставят экзамен, если студент хоть что-то знает = ) Иными словами, логическое ИЛИ скрывает за собой связку «хотя бы на один» (и она вовсе не означает, что СТРОГО на один!).

Ну и давайте отвлечёмся от бытового электричества: подавляющее большинство сайтов Интернета расположены на профессиональных серверах, которые снабжаются, как правило, двумя блоками питания. В электротехнике это называется параллельным подключением, которое как раз и моделирует правило ИЛИ – сервер работает, если исправен хотя бы один блок питания. Оборудование, кстати, поддерживает «горячую» замену, т.е. сгоревший БП можно заменить, не выключая сервер. Такая же история с жёсткими дисками – они дублируются в так называемом RAID-массиве, и более того, сам Дата-центр, где находятся серверы, обычно запитывается двумя независимыми электролиниями + дизель-генератор на всякий случай. Эти меры позволяют обеспечить максимальный аптайм сайтов.

И коль скоро речь зашла о компьютерах, то они… базируются на рассмотренных логических операциях! Это кажется невероятным, но задумаемся – а что вообще могут «понимать» эти «железки»? А понимать они могут следующее:

в проводе есть ток – это логическая единица;
провод обесточен – это логический ноль.

Именно данный факт первопричина того, что в основе измерения объёма информации лежит степень двойки:
и т.д.

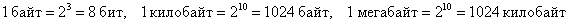
Простейшим «компьютером» является… обычный выключатель – он хранит информацию в 1 бит (истину или ложь в указанном выше смысле). Центральный же процессор современного компьютера насчитывает сотни миллионов (!) транзисторов, и самое сложное программное обеспечение, самая «навороченная игра» раскладывается на множество нулей и единиц, которые обрабатываются с помощью элементарных логических операций!

И уже следующие две операции, которые мы рассмотрим, являются не самостоятельными, то есть могут быть выражены через отрицание, конъюнкцию и дизъюнкцию:

Импликация и логическое следствие.
Необходимое условие. Достаточное условие

До боли знакомые обороты: «следовательно», «из этого следует это», «если, то» и т.п.

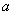
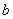
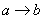
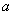
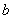
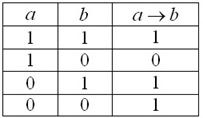
Импликацией высказываний (посылка) и (следствие) называют высказывание , которое ложно в единственном случае – когда истинно, а – ложно:

Фундаментальный смысл операции таков (читаем и просматриваем таблицу сверху вниз):

из истины может следовать только истина и не может следовать ложь;

изо лжи может следовать всё, что угодно (две нижние строчки), при этом:

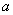
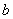
истинность посылки является достаточным условием для истинности заключения ,

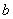
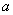
а истинность заключения – является необходимым условием для истинности посылки .

Разбираемся на конкретном примере:

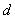
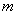
Составим импликацию высказываний – идёт дождь и – на улице сыро:

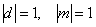
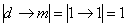
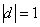
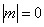
Если оба высказывания истинны , то само собой истинна и импликация – если на улице идёт дождь, то на улице сыро. При этом не может быть такого, чтобы дождь шёл , а на улице было сухо :

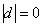
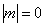
Если же дождя нет , то на улице может быть как сухо :

так и сыро :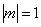
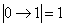
(например, по причине того, что растаял снег).

А теперь ВДУМЫВАЕМСЯ в эти «штампованные» слова необходимость и достаточность:

Дождь является достаточным условием для того, чтобы на улице было сыро, и с другой стороны, сырость на улице необходима для предположения о том, что прошёл дождь (ибо если сухо – то дождя точно не было).

Обратная же импликация нелегальна: – сырости на улице ещё не достаточно для обоснования факта дождя, и, кроме того, дождь ведь не является НЕОБХОДИМОЙ причиной сырости (т.к., например, может пройти и растаять град).

Вроде бы должно быть понятно, но на всякий случай ещё несколько примеров:

– Чтобы научиться выполнять действия с матрицами, необходимо уметь складывать и умножать числа. Но этого, как вы правильно предчувствуете, не достаточно.

– Чтобы научиться выполнять арифметические действия достаточно окончить 9 классов. Но это не является условием необходимым – считать может научить и бабушка, причём ещё в детском саду.

– Чтобы найти площадь треугольника достаточно знать его сторону и высоту, проведённую к этой стороне. Однако опять же – это не необходимость, площадь треугольника можно найти и по трём сторонам (формуле Герона) или, например, с помощью векторного произведения.

– Для допуска к экзамену по высшей математике Пете необходимо отчитаться по курсовой работе. Но этого не достаточно – потому что ещё нужно сдать зачёт.

– Для того чтобы вся группа получила зачёт достаточно занести преподавателю ящик коньяка. И здесь, как нетрудно предположить, отпадает необходимость что-либо учить =) Но, обратите внимание, подготовка вовсе не возбраняется 😉

Бывают ли условия необходимые и в то же время достаточные? Конечно! И очень скоро мы до них доберёмся. А сейчас об одном важном принципе матлогики:

Математическая логика формальна

Её интересует истинность или ложность высказываний, но не их содержание! Так, если мы составим импликацию Если черепахи не летают, то дважды два равно четырём, то она будет истинной! Иными словами, любое истинное высказывание можно обосновать любой истиной (1-я строчка таблицы), и с точки зрения формальной логики это будет истина!

Но ещё интереснее ситуация с ложным посылом: любой ложью можно обосновать всё, что угодно – как истину так и ложь:

– если Луна квадратная, то ;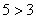
– если пингвины ходят в валенках, то черепахи носят шлёпанцы.

А что? – по таблице оба высказывания истинны!

Данные факты получили название парадокс импликации, но в действительности мы, конечно же, рассматриваем примеры, осмысленные с точки зрения нашей содержательной логики.

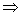
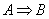
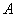
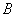
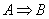
И ещё один очень важный момент: импликацию часто обозначают значком (тоже читается «следовательно», «из этого следует это»), который мы также используем в ходе решения задач, доказательств теорем и т.д. И здесь речь идёт о совпадении обозначений – то, что мы используем в «обычных» математических выкладках, строго говоря, не является импликацией. В чём отличие? Когда мы решаем задачу и пишем, что («из а следует бэ»), то полагаем высказывание заведомо истинным, и более того, выводим из него другую истину . В математической логике это называется логическим следствием. Обычно следствие подлежит обоснованию, и поэтому при оформлении работ всегда старайтесь пояснять, какие аксиомы, теоремы, решённые задачи и т.д. вы использовали для того или иного вывода.

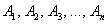
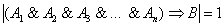
Теорема по своей сути тоже представляет собой логическое следствие: её условие опирается на истинные посылки (аксиомы, ранее доказанные теоремы и т.д.). Доказательство же устанавливает истинность следствия , причём в этом процессе не могут использоваться ложные рассуждения.

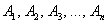
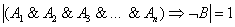
Недоказанная теорема называется гипотезой, и варианта тут два: либо она выводит из истины истину и представляет собой теорему, либо гипотеза невернА, т.е. из множества истинных посылок следует «не бэ»: . В случае опровержения получается тривиальный вывод наподобие «гипотеза Ивана Петрова неверная», но и это, бывает, дорогого стОит – дерзайте, уважаемые читатели!

Рассмотрим в качестве примера, конечно, не мегатеорему, но утверждение, которое требует пусть простого, но обоснования. Хотя и его не будет =) =):

– число делится на 4;
– число делится на 2.

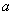
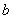
Очевидно, что следствие 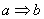истинно, то есть из того, что число делится на 4, следует и его делимость на 2. И, соответственно, противоположное заключение – есть ложь:

При этом ещё раз обращаю внимание, что посылка 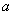изначально постулируется как истина (в отличие от импликации, где она может быть и ложной).

Для логических следствий также в ходу понятия необходимости и достаточности, скопирую пару строк сверху:

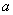
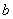
истинность посылки – это достаточное условие для истинности заключения ,

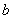
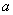
истинность заключения – это необходимое условие для истинности посылки .

Делимость числа на 4 является достаточным условием для того, чтобы оно делилось на 2. И с другой стороны, делимость числа на 2 является необходимым условием делимости на 4.

Следует отметить, что рассмотренный пример можно записать и в виде импликации:
(пользуясь таблицей, проанализируйте все расклады самостоятельно)

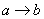
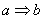
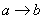
Однако в общем случае «перенос понятий» некорректен! То есть, если мы ведём разговор о том, что , то это ещё не значит, что будет справедлива импликация . И такой пример я приведу в заключительном пункте.

Как уже отмечалось, на практике импликацию часто обозначают значком 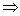, но чтобы не возникло путаницы, я намеренно использовал одиночную стрелку.

Да, чуть не забыл – импликацию можно выразить через предыдущие операции. …Но об этом, пожалуй, во второй части о формулах и законах логики, а то у меня и так неслабый трактат получился.

Эквиваленция. Необходимое и достаточное условие

Эквиваленция обозначается значком 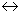и читается «тогда и только тогда»

Наверное, многие догадываются, что это за операция:

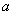
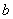
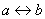
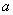
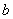
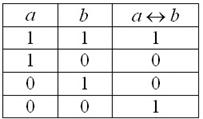
Эквиваленцией высказываний и называют высказывание , которое истинно в том и только том случае, когда высказывания и истинны или ложны одновременно:

Данная операция естественным образом выражается формулой 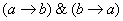– «из а следует бэ и из бэ следует а».

Предположим, что Петя вышел на финишную черту сессии, и ему осталось сдать 3 экзамена:

– три экзамена сданы;
– сессия успешно завершена.

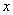
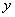
Очевидно, что при описанных выше обстоятельствах эти высказывания эквиваленты:

– сессия успешно завершена тогда и только тогда, когда сдано 3 экзамена.

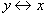
Перед вами пример необходимого и достаточного условия: для того чтобы завершить сессию успешно Пете необходимо сдать 3 экзамена (в противном случае сессия будет не сдана) и в то же самое время этого достаточно (т.к. больше ничего делать не нужно).

Особенность эквиваленции состоит в том, что имеет место либо и то и другое, либо ничего, например:

Петя занимается штангой тогда и только тогда, когда Маша танцует на столе

Это значит, что либо Петя занимается штангой и Маша танцует на столе, либо они оба лежат на диване Пётр, ты заслужил! =) Такие вот дружные Петя и Маша. Теперь вроде бы похожая фраза без «тогда и только тогда»:

Петя занимается штангой, когда Маша танцует на столе

Но смысл несколько поменялся: здесь можно предположить, что Петя, бывает, тягает штангу и без Маши, и другой стороны, Маше «до лампочки», качается ли во время её танца Петя.

Вот в чём сила необходимого и достаточного условия! – оно объединяет и дисциплинирует =)

…хотел я для прикола распределить роли наоборот, но затем передумал… всё-таки нельзя такое пропагандировать =)

К слову, о дисциплине – рациональный подход как раз и предполагает необходимость и достаточность – когда человек для достижения какой-либо цели делает ровно столько, сколько нужно, и не больше. Это, конечно, бывает скучно в обычной жизни, но всячески приветствуется в математических рассуждениях, которые нас уже заждались:

Треугольник является равносторонним тогда и только тогда, когда у него равные углы

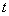
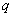
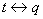
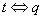
Высказывания – треугольник равносторонний и – у него равные углы можно соотнести эквиваленцией , но на практике мы почти всегда связываем их обоюдоострым значком логического следствия , который тоже читается «тогда и только тогда». Отличие от эквиваленции такое же:

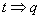
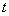
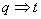
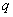
– когда мы утверждаем, что , то изначально полагаем высказывание истиной (и никак не ложью). И наоборот, запись подразумевает безусловную истинность посылки .

И в заключение первой части урока вспомним знаменитую теорему, которую я переформулирую «по-взрослому»:

Для того, чтобы треугольник был прямоугольным необходимо и достаточно, чтобы квадрат одной из его сторон равнялся сумме квадратов двух других сторон:

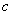
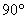
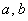
Напоминаю, что сторона называется гипотенузой (бОльшая сторона, лежащая напротив угла ), а стороны – катетами.

Перепишем теорему в сокращённой записи:
– треугольник прямоугольный – выполнено

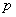
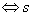
Доказательство «теорем такого типа» состоит из 2 частей, у которых тоже есть стандартные названия (наверное, неоднократно сталкивались):

1) Необходимость (условия ):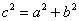
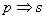
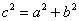
– иными словами, тут нужно доказать, что для того, чтобы треугольник был прямоугольным, необходимо выполнение равенства .

Данный пункт – это собственно и есть теорема Пифагора, формулировка которой нам знакома ещё со школы: «Если треугольник прямоугольный, то ».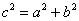

2) На втором шаге обосновывается достаточность:
– здесь надо доказать, что справедливость равенства достаточна для того, чтобы треугольник был прямоугольным.

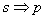
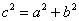
Учащихся опять же такими словами не запугивают, и второй пункт формулируют в виде обратной теоремы Пифагора: «Если 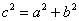, то треугольник прямоугольный».

Связей по схеме «тогда и только тогда» в математике очень много, и я только что привёл стандартную схему их доказательства. И, конечно же, всегда анализируйте, что означают «необходимо», «достаточно», «необходимо и достаточно» в том или ином случае.

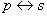
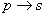
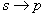
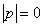
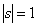
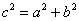
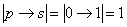
Следует отметить, что теорему можно рассмотреть с точки зрения логической операции , но вот запись (как и обратная запись ) становится нелегальной! Почему? Пусть – треугольник не прямоугольный, – равенство выполнено. Но тогда по импликационной таблице получаем , что не соответствует действительности!

Но зато записи 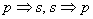совершенно законны, поскольку логическое следствие отталкивается исключительно от истины!

Жду вас во второй части нашего увлекательного урока, где мы познакомимся с основными логическими формулами и законами, а также порешаем практические задачи. Для решения задач потребуется пять табличек с этой страницы, поэтому я рекомендую сразу переписать их на листок – чтобы они были перед глазами.

Кроме того, я открою вам секрет успешного изучения математической логики 😉

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник