Что такое вычислительная ошибка
Классификация ошибок, влияющих на снижение оценки
При проверке математических знаний следует различать грубые и негрубые ошибки.
К грубым ошибкам относятся:
-Вычислительные ошибки в заданиях;
-Ошибки в определении порядка выполнения арифметических действий;
-Неправильное решение задачи (пропуск действий (действия)), неправильный подбор действий (действия), лишние действия;
-Незаконченное решения задачи или примера;
-Невыполненное задание (не приступил к его выполнению) ;
-Незнание или неправильное применение свойств, правил, алгоритмов, существующих зависимостей, которые лежат в основе задач или используются в ходе их выполнения;
-Несоответствие пояснительного текста, задания, названия величин выполненным действиям и полученным результатам;
-Несоответствие выполненных измерений и геометрических построений данным параметрам задачи.
Негрубыми ошибками являются:
-Нерациональные приемы вычисления, если ставились требования воспользоваться такими приёмами;
-Неправильное построение или постановка вопросов к действиям (действия) при решении задачи;
-Неправильное или неграмотное с точки зрения стилистики или по содержанию формулировки ответа задачи;
-Неправильное списывание данных (цифр, знаков) задачи с правильным ее решением;
-Не закончено (не доказано) до логического конца преобразования;
-Ошибки в записях математических терминов, символов;
-Отсутствие ответа в задании или ошибки в записи ответа.
Две негрубым ошибки считают одной грубой ошибки.
Опрятные исправления являются недостатками работы.
За грамматические ошибки, допущенные в работе, оценка по математике не снижается.
За неаккуратно оформленную работу оценка по математике может быть снижена на 1 балл, но не ниже «3», и не в контрольной работе.
Продолжительность выполнения проверочных письменных работ: во 2-м классе начальной школы: I семестр — до 20 мин, II семестр — до 30 мин, 3 — 4-й классы — до 35 мин. За это время ученикам нужно успеть не только полностью выполнить работу, но и проверить ее.
Работа, состоящая из примеров
| Отметка | Характеристика учебных достижений обучающихся |
| Ученикдопускает 4 и более грубых ошибок. | |
| Ученикдопускает 2–3 грубые и 1–2 негрубые ошибки или 3 и более негрубых ошибки. | |
| Ученикдопускает 1 грубую и 1–2 негрубыеошибки. | |
| Ученик выполняет работубез ошибок. |
Работа, состоящая из задач
| Отметка | Характеристика учебных достижений обучающихся |
| Ученикдопускает 2 и более грубых ошибки. | |
| Ученикдопускает 1 грубую и 3–4 негрубыеошибки, правильно выполнено не менее 50% работы. | |
| Ученикдопускает 1 грубую и 1–2 негрубыеошибки. | |
| Ученик выполняет работубез ошибок. |
Комбинированная работа (1 задача, примеры и задание другого вида)
| Отметка | Характеристика учебных достижений обучающихся |
| Ученикдопускает ошибки в ходе решения задачи и хотя быодна вычислительная ошибка или при решении задачи и примеров допущено более 5вычислительных ошибок. | |
| Ученикдопускает ошибки в ходе решения задачи при правильном выполнении всехостальных заданий или допущены 3-4 вычислительные ошибки, при этом ходрешения задачи должен быть верным. | |
| Ученикдопускает 1-2 вычислительные ошибки. | |
| Ученик выполняет работубез ошибок и исправлений. |
Контрольная работа диагностического характера
Егор Вышегородцев | Ошибки танцевальных пар, влияющие на судейскую оценку
Приложение А. Погрешности вычислений
Абсолютная и относительная погрешности
Точность полученного в результате вычисления результата определяется погрешностью вычислений. Различают два вида погрешностей – абсолютную и относительную.
Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения:
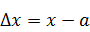
где а – приближенное значение числа х.
Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа:
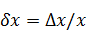
Истинное значение величины х обычно неизвестно. Имеется лишь приближенное значение а и нужно найти его предельную погрешность 

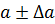
Источники погрешностей
Рассмотрим различные причины возникновения погрешностей.
Математическая модель задачи является неточной
Погрешность возникает из-за того, что сам численный метод или математическая модель является лишь приближением к точному методу (например, дифференцирование). Кроме того, любая математическая модель или метод могут внести существенные погрешности, если в ней не учтены какие-то особенности рассматриваемой задачи. Модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других. Такую погрешность называют также методической. Она всегда имеет место, даже при абсолютно точных данных и абсолютно точных вычислениях. В большинстве случаев погрешность численного метода можно уменьшить до требуемого значения за счет изменения параметров метода (например, уменьшением шага дискретизации, или увеличением количества итераций).
Ошибки в исходных данных
Исходные данные задачи часто являются основным источником погрешностей. Ошибки такого типа неизбежны и проявляются в любых реальных задачах, поскольку любое измерение может быть проведено с только какой-то предельной точностью. Вместе с погрешностями, вносимыми математической моделью, их называют неустранимыми погрешностями, поскольку они не могут быть уменьшены ни до начала решения задачи, ни в процессе ее решения.
Следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других не приводит к повышению точности конечных результатов. Если какие-то отдельные точки данных (измерения) явно ошибочные, их можно исключить из вычислений.
Вычислительные ошибки (ошибки округления)
Ошибки этого типа проявляются из-за дискретной (а не непрерывной) формы представления величин в компьютере. Вычислительные ошибки можно свести к минимуму продуманно организовывая алгоритмы.
Вычислительные ошибки
Рассмотрим подробнее вычислительные ошибки. Допустим, исходные данные не имеют погрешности, но поскольку место в памяти компьютера, отведенное на хранение чисел, ограничено, и соответственно ограничена точность представления чисел, возникновение вычислительных ошибок неизбежно.
Представление чисел с плавающей точкой
Для хранения целых чисел (int, long, unsigned int и т.д.) обычно отводится 4 байта памяти, что позволяет представлять целые числа, находящиеся примерно в диапазоне от 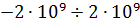
В вычислениях чаще используются вещественные числа (float, double). Такие числа представляются в компьютере в форме с плавающей точкой, и хранятся в логарифмическом виде – мантисса и порядок:
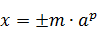
где m – мантисса, p – порядок, а – основание степени.
Например, число 273.9 можно 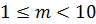
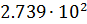
В таблице А.1 приводится диапазон допустимых значений и другие параметры для чисел с плавающей точкой одинарной (float) и двойной (double) точности.
| Точность | Одинарная | Двойная |
| Размер (байты) | 4 | 8 |
| Наименьшее значение | 1.2·10 −38 | 2.3·10 −308 |
| Наибольшее значение | 3.4×10 +38 | 1.7×10 +308 |
| Размеры степени и мантиссы (биты) | 8-23 | 11-52 |
Таблица A.1. Диапазон чисел, представимых в формате с плавающей точкой
Для чисел с плавающей точкой существует понятие машинного эпсилон – наименьшего положительного число ε такого, что 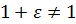
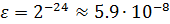
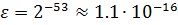
Погрешность округления
При вычислениях с помощью компьютера неизбежны погрешности округлений, связанные с ограниченностью хранимых разрядов мантиссы. Для приближенного числа, полученного в результате округления, абсолютная погрешность 
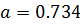
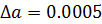
Перевод чисел из одной системы счисления в другую также может быть источником погрешности из-за того, что основание одной системы счисления не является степенью основания другой (например, 10 и 2). Это может привести к тому, что в новой системе счисления число невозможно представить абсолютно точно, например:
Погрешность арифметических действий над приближенными числами
При выполнении операций над приближенными числами можно оценить предельную погрешность результата в зависимости от выполняемой операции. При умножении или делении чисел друг на друга их относительные погрешности складываются:
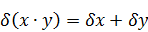
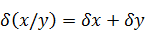
При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени:
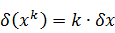
При сложении или вычитании чисел их абсолютные погрешности складываются:
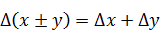
Относительная погрешность суммы положительных слагаемых вычисляется как:
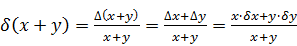
Отсюда следует, что относительная погрешность суммы нескольких чисел одного и того же знака, заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:
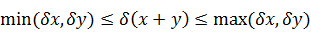
На практике для оценки погрешности при сложении чисел обычно используют максимальную погрешность 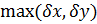
При сложении погрешность будет сильно завесить от абсолютных величин складываемых чисел. Рассмотрим пример сложения двух чисел с одинаковым количеством значащих цифр, но разных по абсолютному значению:
1234 + 0.005678 = 1234.00005678
или в компьютерном представлении:
1.234Е+03 + 5.678Е-03 = 1.234005678Е+03
После сложения количество значащих цифр равно 10. Число с одинарной точностью (float) позволяет хранить только 8 значащих цифр, то есть на самом деле число будет равно 1.2340056Е+03. Две значащие цифры потерялись в процессе сложения. Потеря точности здесь возникает из-за того, что при прибавлении к большому числу малых чисел результат сложения выходит за пределы точности при округлении. Для того чтобы уменьшить погрешность вычислений, нужно складывать числа в порядке возрастания их абсолютной величины. Таким образом можно минимизировать абсолютную величину промежуточной погрешности при каждом сложении.
Рассмотрим теперь вычитание чисел (сложение чисел разного знака, или вычитание чисел одного знака). В соответствии с выражением (А.7) относительная погрешность может быть очень большой в случае, если числа близки между собой, так как даже при малых погрешностях 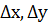
Таким образом, можно сделать вывод, что сложение и вычисление являются плохо обусловленными (неустойчивыми) операторами, так как при некоторых данных даже небольшая погрешность в исходных данных может привести к большой погрешности результата. Уменьшить погрешность можно за счет правильной последовательности операций. Из-за погрешности округления в машинной арифметике важен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются.
Ошибки на ЕГЭ по математике и причины их появления
Прочтите статью об ошибках на ЕГЭ, подготовленную по моей просьбе репетитором по математике из подмосковного Зеленограда Ермаковой Дианой. Я приложил к статье свою руку в качестве редактора — консультанта.
Почему ребята допускают те или иные ошибки на ЕГЭ по математике? Почему за безошибочные работы снимают баллы?
Сразу после обнародования результатов экзамена я проанализировала сканеры учеников, которых, будучи репетитором по математике, готовила к ЕГЭ длительное время. Были сделаны определенные выводам. Я не буду рассматривать здесь случаи, когда ученик вообще не умеет решать характерные типы задач, не берется за них или берется, но пишет откровенную ерунду. Рассмотрю лишь ошибки в заданиях, которые школьники обычно решают более-менее уверенно.
Причины ошибок на ЕГЭ по математике — часть «В».
Здесь я остановлюсь подробно только на вычислительных ошибках, поскольку в сканах работ не отражается сам ход решения и проверить его невозможно.
Первая причина
То, что многие ребята плохо считают без калькулятора — не секрет. Но и те, которые считают хорошо, тоже допускают вычислительные ошибки. Причина видится не только в банальной невнимательности, но и в том, что порой учащимся не хватает умения и/или желания заниматься проверками полученные результатов. Ошибки некоторых заданий «В» всплывают на поверхность сами, проявляя явные числовые или житейские коллизии. Например, получив в задаче об оплате за свет в текущем месяце сумму в 300 тысяч рублей, ученик не задумываясь, переносит ее в бланк. Но разве она может равняться полугодовой зарплате среднестатистического работника? Ответ в В5 и В12 можно всегда проверить подстановкой полученного ответа в исходное уравнение и т.д.
Нужно ли репетитору по математике обучать проверке ответа?
Не только можно, но и нужно. Вопрос только в том, какие задания давать для реализации этого замысла. В обязательном порядке включаются примеры серии «найди ошибку в решении», «проверь полученный ответ подстановкой в уравнение (систему)» и т.д. Вместе с репетитором по математике проводится анализ сканеров работ с реального ЕГЭ, которые в большом количестве есть в пособиях для подготовки экспертов на сайте ФИПИ.
Вторая причина
Часто человек, который дружит с математикой не первый год, часто может решить одну и ту же задачу разными способам. Соответствующий опыт решения позволяет не только искать, но и реалозывать тот или иной план. В силу возрастных особенностей детей школьники выдают репетитору по математике далеко не всегда рациональные решения. Громоздкий пути — рассадник целого спектра ошибок, с которым нужно бороться.
Математические ошибки в части С
Кроме уже описанных выше вычислительных ошибок, здесь ученики допускают промахи еще и логическо — смыслового характера.
В задании С1 ошибки встречаются реже всего. В основном, они связаны не с тригонометрией, а с алгебраическими преобразованиями (потеря знака, неверное извлечение корня при решении простейшего квадратного уравнения и т.д).
Ошибки в тригонометрии связаны обычно или с нетвердым знанием значений функций табличных углов (или непонимании, как решаются простейшие тригонометрические уравнения), или с тем, что ребята путаются в расположении корней на тригонометрическом круге. Для тех, кто отбирает корни с помощью двойного неравенства, наиболее типична ошибка в преобразованиях или при верных преобразованиях потеря значений параметра N. Ребята не замечают, что в интервал входит целое значение N или, наоборот, считают, что в интервал попадает значение, которого там нет. Здесь я рекомендую всегда рисовать ось действительных чисел, сначала расставив на ней целые значения, обозначив их жирными точками, а потом полученные интервалы.
Тригонометрический круг — важнейший инструмент репетитора по математике для механики объяснений. С первых же уроков на синусы и косинусы репетитору необходимо нагружать ученика заданиями на отображение углов на круге, а в перспективе учить отбору корней, удовлетворяющих условию (через представление об оси, как о спирали). Своевременные объяснения и четкие инструкции репетитора по математике, направленные на тренировку отбора позволяет разобраться в оборотах, четвертях, положительном и отрицательном направлении обхода, в расположении корней на круге.
Встречались работы, в которых снимали баллы за оформление. Например, за то, что не обоснован отбор корней, или за то, что необоснованно деление на cosX обеих частей уравнения. Плох тот репетитор по математике, кто в процессе подготовки к ЕГЭ не уделяет вермя на отработку грамотного оформления решений. Это приводит к обидной потере баллов в реальных работах даже при полностью верном ответе.
В задании С2 чаще всего встречается недостаточно полное обоснование решения. Геометрия для ребят традиционно сложнее алгебры, так как связана с тем, что на чертеже не только надо уметь видеть расположение объектов, но и доказывать это расположение. Необходимо учиться доказывать каждый шаг в решении, не пропуская ни одного важного перехода. Это не значит, что надо углубляться в дебри доказательств, доходя до аксиом 7 класса, но важные моменты, например, перпендикулярность диагоналей дельтоида, которое используется при нахождении его площади, обосновать необходимо. Именно на этой перпендикулярности или на том, что сечение построено, но никак не описано его построение, ребята теряли балл.
В сканах своих учеников в двух работах я обнаружила в решении системы неравенств С3 абсолютную чепуху, которую и решением-то назвать нельзя. При этом ребята на уроках решали эти задания почти уверенно, но на экзамене не справились даже с дробно-рациональным уравнением, в котором не нужно ни проверять ОДЗ, ни знать равносильность переходов. Причина проста: ни один из них не принес мне ни одного домашнего задания по С3, хотя я предупреждала, что решать на уроках с репетитором, который поможет, подскажет, направит, исправит ошибки — одно, а решать дома, когда остаешься с заданием один на один — совсем другое. В итоге выявилось, что они вообще не понимают, что надо делать в неравенствах, хотя при объяснении я всегда стараюсь дать суть решения, а не научить механическим действиям. Например, наиболее распространены ошибки в ОДЗ логарифмических неравенств. Ребята не понимают, что логарифм — это показатель степени. Почему основание логарифма должно быть не равно единице? Да потому, что единица в любой СТЕПЕНИ даст единицу, поставив которую в основание мы изменим функцию до «неузнаваемости». Ее область определения превратится в вырожденную точку, сама функция получится неоднозначной, а если считать ее многозначной, то графиком уравнения 
Еще одна распространенная ошибка в С3 как под копирку встречается в большинстве работ, хотя в течение года очень много времени я уделяю сути метода интервалов. Дробно — рациональное неравенство путают с уравнением, отбрасывая знаменатель и не учитывая знаки знаменателя. Опять непонимание сути выполняемых действий: при решении уравнения мы ищем корни, точки пересечения с осями, поэтому приравниваем к нулю числитель, проверив неравенство нулю знаменателя, а при решении уравнения мы ищем интервалы, в которых функция принимает нужный знак. Отбросив знаменатель, мы получим ДРУГУЮ ФУНКЦИЮ с другими знаками. В течение года я строила ребятам графики исходной функции и той функции, которая получается в результате избавления от знаменателя, показывая, что они имеют разный вид и разные знаки на промежутках.
Ошибки в С3 могут быть очень разнообразны, начиная от вычислительных и заканчивая системными, поэтому рассмотреть их все в рамках одной статьи, конечно, не представляется возможным. Единственный момент, на который я в итоге хочу обратить внимание — С3 нельзя решать по шаблону, без понимания выполняемых действий. Также при решении этого задания необходимо быть максимально внимательным и сосредоточенным, поскольку задание имеет большую смысловую нагрузку и объем вычислений, и сделать ошибку легко может даже очень хороший ученик.
Наконец, в одной из работ моей довольно толковой ученицы я встретила очень обидную вещь, объяснить которую я могу только паникой и испугом, потому что она никогда не делала подобных ошибок. Кстати, еще одна причина ошибок — страх перед экзаменом, который упорно культивируют в детях весь период обучения и учителя, и родители, и даже, к сожалению, некоторые репетиторы. Это в принципе нельзя допускать, так как психика у детей еще не сформирована, у них решается судьба поступления в ВУЗы, огромна нагрузка по всем предметам, а их тут еще и ЕГЭ пугают.
Девочка решила дробно-рациональное неравенство, правильно расставила знаки на осях. Осталось списать с оси ответ. И тут она начинает вычислять какое-то несуществующее ОДЗ (числитель больше нуля, знаменатель больше нуля. ) Сказала, что растерялась и запаниковала. Перепутала дробно-рациональное неравенство с логарифмическим. Ну, что тут скажешь? Перед этим бессилен даже профессиональный репетитор по математике с немалым сажем. Разве что применять методику специального запутывания и отвлекания ученика на уроках, но она подходит только сильным ученикам с устойчивой психикой. Слабого она только испугает и вызовет лишнюю панику.
В задачах С4 я встретила только незнание функции половинного угла, в результате чего решение не было доведено до конца. Причем именно на тригонометрию в геометрии я обычно делала особый упор. От углов можно было легко уйти к вычислению площади через высоту и основание, но ребята то ли не увидели этого, то ли зациклились на формуле площади треугольника через синус, потому что углы были даны в задаче. Были также и случаи, когда ученик не увидел или не захотел рассматривать второй вариант чертежа.
Особо хотелось бы поговорить о задании С5. Ребята, которые умеют решать С5, обладают высоким уровнем математической культуры, поэтому редко допускают вычислительные ошибки. Но критерии проверки этого задания традиционно очень строгие. При обучении графическим методам решения этого вида заданий репетитор по математике должен обратить внимание на следующие вещи:
1. Нужно расписывать решение как можно более подробно и обоснованно. Не обязательно писать дискриминант квадратного уравнения, но все важные переходы должны быть описаны и разъяснены.
2. Необходимо задавать функции обеих частей уравнения (неравенства).
3. Если функция элементарная, достаточно ее построить так, как учили в школе и назвать вид полученного графика.
4. Если функция не является элементарной, необходимо ее ПОЛНОСТЬЮ исследовать на монотонность, экстремумы и пересечение с осями координат. В этом году многие не увидели полуокружность и строили «по точкам», что недопустимо и грозило потерей 2-3 баллов.
5. Все положения графика с параметром должны быть обязательно описаны (даже те, которые не используются). Таким образом доказывается, что при других значениях параметра нужных нам решений не будет.
При соблюдении указанных выше условий и отсутствии вычислительных ошибок велика вероятность получить за задание максимальный балл. Ребята ленятся расписывать решение подробно и упускают важные переходы, за что получают меньше максимального на 1 — 2 — 3 балла.
Полное избавление ребят от ошибок для репетитора по математике — неподъемная задача, но нужно стремиться уменьшать вероятность оплошностей. Выделять время не только на решение задач, но и предлагать специальные задания для самоконтроля. Важно научить внимательно и просто вести записи. Время на ЕГЭ ограничено и поэтому внимание репетитора в конце года должно быть сосредоточено на скорости решения. Кроме этого также правильному распределению времени в зависимости от того, на какой балл ученик претендует.
Ермакова Диана Владимировна, репетитор по математике, г. Зеленоград.