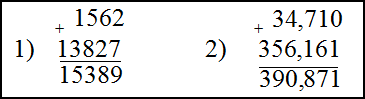Что такое вычисление чисел
Красота чисел. Как быстро вычислять в уме

Старинная запись на квитанции в уплате подати («ясака»). Она означает сумму 1232 руб. 24 коп. Иллюстрация из книги: Яков Перельман «Занимательная арифметика»
Ещё Ричард Фейнман в книге «Вы конечно шутите, мистер Фейнман!» поведал несколько приёмов устного счёта. Хотя это очень простые трюки, они не всегда входят в школьную программу.
Например, чтобы быстро возвести в квадрат число X около 50 (50 2 = 2500), нужно вычитать/прибавлять по сотне на каждую единицы разницы между 50 и X, а потом добавить разницу в квадрате. Описание звучит гораздо сложнее, чем реальное вычисление.
52 2 = 2500 + 200 + 4
47 2 = 2500 – 300 + 9
58 2 = 2500 + 800 + 64
Молодого Фейнмана научил этому трюку коллега-физик Ханс Бете, тоже работавший в то время в Лос-Аламосе над Манхэттенским проектом.
Ханс показал ещё несколько приёмов, которые использовал для быстрых вычислений. Например, для вычисления кубических корней и возведения в степень удобно помнить таблицу логарифмов. Это знание очень упрощает сложные арифметические операции. Например, вычислить в уме примерное значение кубического корня из 2,5. Фактически, при таких вычислениях в голове у вас работает своеобразная логарифмическая линейка, в которой умножение и деление чисел заменяется сложением и вычитанием их логарифмов. Удобнейшая вещь.

Логарифмическая линейка
До появления компьютеров и калькуляторов логарифмическую линейку использовали повсеместно. Это своеобразный аналоговый «компьютер», позволяющий выполнить несколько математических операций, в том числе умножение и деление чисел, возведение в квадрат и куб, вычисление квадратных и кубических корней, вычисление логарифмов, потенцирование, вычисление тригонометрических и гиперболических функций и некоторые другие операции. Если разбить вычисление на три действия, то с помощью логарифмической линейки можно возводить числа в любую действительную степень и извлекать корень любой действительной степени. Точность расчётов — около 3 значащих цифр.
Чтобы быстро проводить в уме сложные расчёты даже без логарифмической линейки, неплохо запомнить квадраты всех чисел, хотя бы до 25, просто потому что они часто используются в расчётах. И таблицу степеней — самых распространённых. Проще запомнить, чем вычислять каждый раз заново, что 5 4 = 625, 3 5 = 243, 2 20 = 1 048 576, а √3 ≈ 1,732.
Ричард Фейнман совершенствовал свои навыки и постепенно замечал всё новые интересные закономерности и связи между числами. Он приводит такой пример: «Если кто-то начинал делить 1 на 1,73, можно было незамедлительно ответить, что это будет 0,577, потому что 1,73 — это число, близкое к квадратному корню из трёх. Таким образом, 1/1,73 — это около одной трети квадратного корня из 3».
Настолько продвинутый устный счёт мог бы удивить коллег в те времена, когда не было компьютеров и калькуляторов. В те времена абсолютно все учёные умели хорошо считать в уме, поэтому для достижения мастерства требовалось достаточно глубоко погрузиться в мир цифр.
В наше время люди достают калькулятор, чтобы просто поделить 76 на 3. Удивить окружающих стало гораздо проще. Во времена Фейнмана вместо калькулятора были деревянные счёты, на которых тоже можно было производить сложные операции, в том числе брать кубические корни. Великий физик уже тогда заметил, что использование таких инструментов, людям вообще не нужно запоминать множество арифметический комбинаций, а достаточно просто научиться правильно катать шарики. То есть люди с «расширителями» мозга не знают чисел. Они хуже справляются с задачами в «автономном» режиме.
Вот пять очень простых советов устного счёта, которые рекомендует Яков Перельман в методичке «Быстрый счёт» 1941 года издательства.
1. Если одно из умножаемых чисел разлагается на множители, удобно бывает последовательно умножать на них.
225 × 6 = 225 × 2 × 3 = 450 × 3
147 × 8 = 147 × 2 × 2 × 2, то есть трижды удвоить результат
2. При умножении на 4 достаточно дважды удвоить результат. Аналогично, при делении на 4 и 8, число делится пополам дважды или трижды.
3. При умножении на 5 или 25 число можно разделить на 2 или 4, а затем приписать к результату один или два нуля.
Здесь лучше сразу оценивать, как проще. Например, 31 × 25 удобнее умножать как 25 × 31 стандартным способом, то есть как 750+25, а не как 31 × 25, то есть 7,75 × 100.
При умножении на число, близкое к круглому (98, 103), удобно сразу умножить на круглое число (100), а затем вычесть/прибавить произведение разницы.
37 × 98 = 3700 – 74
37 × 104 = 3700 + 148
4. Чтобы возвести в квадрат число, оканчивающееся цифрой 5 (например, 85), умножают число десятков (8) на него же плюс единица (9), и приписывают 25.
8 × 9 = 72, приписываем 25, так что 85 2 = 7225
Почему действует это правило, видно из формулы:
(10Х + 5) 2 = 100Х 2 + 100Х + 25 = 100Х (X+1) + 25
Приём применяется и к десятичным дробям, которые оканчиваются на 5:
5. При возведении в квадрат не забываем об удобной формуле
(a + b) 2 = a 2 + b 2 + 2ab
44 2 = 1600 + 16 + 320
Алгебра. Урок 1. Числа и вычисления
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Действия с дробями
Понятие обыкновенной, десятичной, смешанной дроби.
Обыкновенная дробь – дробь вида
где число a – числитель дроби, число b – знаменатель.
Примеры:
Обыкновенная дробь может быть правильной или неправильной, сократимой или несократимой:
Основное свойство обыкновенной дроби:
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число (натуральные числа – числа, которые используются при счете: 1, 2, 3, …), то получится дробь, равная данной.
Смешанную дробь всегда можно перевести в неправильную обыкновенную дробь.
3 1 2 = 3 ⋅ 2 + 1 2 = 7 2
2 7 8 = 2 ⋅ 8 + 7 8 = 23 8
90 12 77 = 90 ⋅ 77 + 12 77 = 6942 77
Десятичную дробь всегда можно перевести в смешанную дробь или в обыкновенную дробь с числителем и знаменателем. Так поступают, когда необходимо совершить действие между обыкновенной дробью и десятичной.
Перевод в смешанные дроби:
56,002 = 56 2 1000 = 56 1 500
56,002 = 56 2 1000 = 56 1 500
Перевод в обыкновенные дроби:
Сложение и вычитание дробей.
Для того, чтобы складывать и вычитать смешанные дроби между собой, необходимо действовать следующим образом:
(1) 2 1 6 + 1 7 8 = 2 ⋅ 6 + 1 6 + 1 ⋅ 8 + 7 8 = 13 6 + 15 8 = 13 ⋅ 4 6 ⋅ 4 + 15 ⋅ 3 8 ⋅ 3 = 52 + 45 24 = 97 24 = 4 1 24
(2) 3 7 12 − 2 3 16 = 3 ⋅ 12 + 7 12 − 2 ⋅ 16 + 3 16 = 43 12 − 35 16 = 43 ⋅ 4 12 ⋅ 4 − 35 ⋅ 3 16 ⋅ 3 = 172 − 105 48 = 67 48 = 1 19 48
(3) 2 3 14 − 0,6 = 2 ⋅ 14 + 3 14 − 6 10 = 31 14 − 3 5 = 31 ⋅ 5 14 ⋅ 5 − 3 ⋅ 14 5 ⋅ 14 = 155 − 42 70 = 113 70 = 1 43 70
Умножение и деление дробей.
При умножении двух дробей числитель первой дроби умножается на числитель второй дроби, знаменатель первой дроби умножается на знаменатель второй:
При делении двух дробей необходимо первую дробь умножить на «перевёрнутую» предыдущую, то есть у дроби-делителя поменять местами числитель и знаменатель и поставить операцию умножения вместо операции деления между этими дробями:
(1) 2 3 4 ⋅ 8 11 ÷ 0,5 = 11 1 4 1 ⋅ 8 2 11 1 ÷ 5 1 10 2 = 2 ÷ 1 2 = 2 ⋅ 2 1 = 4
(2) 6 ÷ 2,25 ⋅ 1,5 = 6 1 ÷ 2 1 4 ⋅ 1 5 1 10 2 = 6 1 ÷ 9 4 ⋅ 3 2 = 6 3 1 ⋅ 4 9 3 ⋅ 3 1 2 1 = 4
Сравнение дробей.
Для того, чтобы сравнивать две дроби между собой, нужно уметь выполнять действия с дробями (сложение, вычитание, умножение, деление). При сравнении дробей, особенно в заданиях, где требуется расположить дроби в порядке возрастания или убывания, удобно приводить обыкновенную дробь к виду десятичной.
Сравнение дробей с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
Примеры:
\[\frac<4> <7>\frac<1><<14>>;\;\;\;\; \frac<2> <3>Сравнение дробей с одинаковыми числителями
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.
Примеры:
\[\frac<2> <7>\frac<7><<11>>;\;\;\;\; \frac<5> <4>> \frac<5><5>.\] Сравнение дробей с разными числителями и знаменателями
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю.
Пример 1:
Приводим дроби к общему знаменателю:
Приходим к выводу, что:
Действия со степенями.
Запись 0 0 в математике не имеет смысла.
Свойства степеней с натуральным показателем:
Что такое вычислить сумму чисел
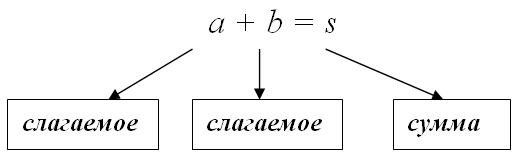
Сумма чисел – это простое (базовое) математическое решение, выражающееся в увеличении исходного числа на заданное.
Визуально операцию суммирования можно представить следующим образом – положите на стол одно яблоко, а затем положите ещё два яблока. Итого получится три яблока. Это и есть сумма чисел яблок.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлено определение суммы чисел и самый простой онлайн калькулятор расчета расчета суммы чисел.
Вычислить сумму чисел до данного
Сделайте три варианта решения:
Пример работы вашей функции:
P.S. Какой вариант решения самый быстрый? Самый медленный? Почему?
Решение с помощью цикла:
Решение через рекурсию:
Решение по формуле: sumTo(n) = n*(n+1)/2 :
P.S. Надо ли говорить, что решение по формуле работает быстрее всех? Это очевидно. Оно использует всего три операции для любого n, а цикл и рекурсия требуют как минимум n операций сложения.
Вариант с циклом – второй по скорости. Он быстрее рекурсии, так как операций сложения столько же, но нет дополнительных вычислительных затрат на организацию вложенных вызовов. Поэтому рекурсия в данном случае работает медленнее всех.
Определение суммы чисел
Задание. Найти сумму чисел:
Ответ.
Свойства суммы чисел
На основании этих свойств можем заключить, что от перестановки мест слагаемых сумма не изменяется.
Дистрибутивность по отношению к умножению
$$(n+m) cdot k=n cdot k+m cdot k$$
Задание. Найти сумму чисел удобным способом:
Решение. По свойствам сложения имеем
При сложении больших чисел или десятичных дробей используется сложение в столбик.
Задание. Найти сумму чисел удобным способом:
Решение. Складываем эти числа в столбик, для этого запишем их друг под другом, разряд под разрядом. В случае десятичных дробей ориентируемся на то, чтобы запятая первого числа стояла под запятой второго. Далее складываем числа стоящие друг под другом, двигаясь справа на лево и записывая результата под чертой дроби. Если сумма чисел в одном столбце превышает десять, то количество десятков прибавляем к числам стоящим в следующем столбце слева от этого столбца:
Сложение рациональных дробей производится по правилу
Задание. Найти сумму чисел:
Решение. Вычислим первую сумму используя правило сложения рациональных чисел
Числитель и знаменатель полученной дроби можно сократить на 2, тогда в ответе получим
Для вычисления второй суммы, преобразуем сначала второе слагаемое в неправильную дробь, для этого умножим целую часть на знаменатель и прибавим полученное число к числителю. Далее применим правило сложение рациональных дробей
Выделим в полученной дроби целую часть, для этого разделим числитель на знаменатель с остатком. Полученное частное запишем в целую часть, а остаток от деления в числитель.
Вычисление
Вычисле́ние — математическое преобразование, позволяющее преобразовывать входящий поток информации в выходной, с отличной от первого структурой. Если смотреть с точки зрения теории информации, вычисление — это получение из входных данных нового знания.
Этот термин используется в широком диапазоне значений, от арифметического вычисления суммы чисел до вычисления шансов на победу в соревновании с использованием сложного эвристического анализа.
Примеры
Умножение 2 на 2 — это простое алгоритмическое вычисление.
Для статистической оценки вероятных результатов выборов на основе опросов общественного мнения также используются алгоритмические вычисления, но результаты представляются не точными числами, а как интервалы вероятностей.
Смотреть что такое «Вычисление» в других словарях:
вычисление — подсчёт, расчёт, счёт, итог, калькуляция, подсчитывание, высчитывание, отсчёт; калькулирование, расчет, прикидка, исчисление, просчитывание, подсчет Словарь русских синонимов. вычисление см. подсчёт Словарь синонимов русского языка. Практический… … Словарь синонимов
ВЫЧИСЛЕНИЕ — ВЫЧИСЛЕНИЕ, вычисления, ср. (книжн. научн.). 1. только ед. Действие по гл. вычислить вычислять. Произвести вычисление. 2. Результат этого действия, то, что получено посредством этого действия. Опубликовать свои вычисления. Толковый словарь… … Толковый словарь Ушакова
вычисление — ВШЫЧИСЛИТЬ, лю, лишь; ленный; сов. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
вычисление — вычисления Процесс выполнения арифметических и логических операций, а также обработки данных с помощью компьютера или других вычислительных средств. См. RISC. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь… … Справочник технического переводчика
ВЫЧИСЛЕНИЕ — получение числового результата некоторым алгоритмом из исходных данных … Большая политехническая энциклопедия
вычисление — ▲ определение (неявного) ↑ величина вычисление определение величины (произвести #). вычислять. счет (устный #). считать (# в уме). высчитать. счетный. расчет. расчетчик. рассчитать. подсчет. подсчитать. просчитать. насчитать. выкладки. прикинуть … Идеографический словарь русского языка
вычисление — skaičiavimas statusas T sritis automatika atitikmenys: angl. calculation; calculus; computation vok. Berechnung, f; Kalkulation, f; Rechnung, f; Zählung, f rus. вычисление, n; исчисление, n; расчёт, m; счёт, m pranc. calcul, m; compte, m … Automatikos terminų žodynas
вычисление — skaičiavimas statusas T sritis Standartizacija ir metrologija apibrėžtis Tam tikro uždavinio sprendimas remiantis kiekybiniais duomenimis. atitikmenys: angl. calculation; counting vok. Rechnen, f; Rechnung, f rus. вычисление, n pranc. calcul, m … Penkiakalbis aiškinamasis metrologijos terminų žodynas
вычисление — apskaičiavimas statusas T sritis chemija apibrėžtis Matematinio uždavinio sprendimas remiantis kiekybiniais duomenimis. atitikmenys: angl. calculation; computation rus. вычисление; исчисление; расчет … Chemijos terminų aiškinamasis žodynas
вычисление — skaičiavimas statusas T sritis fizika atitikmenys: angl. calculation; computation; counting vok. Rechnen, n; Rechnung, f; Zählung, f rus. вычисление, n; расчёт, m; счёт, m pranc. calcul, m … Fizikos terminų žodynas
Алгебра. Урок 3. Вычисления и алгебраические выражения
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Преобразования и вычисления
Свойства степеней:
(3) ( a ⋅ b ) n = a n ⋅ b n
(4) ( a b ) n = a n b n
Свойства квадратного корня:
18 = 9 ⋅ 2 = 9 ⋅ 2 = 3 2
(4) a 2 = | a | при любом a
Рациональные и иррациональные числа
Рациональные числа – числа, которые можно представить в виде обыкновенной дроби m n где m – целое число ( ℤ = 0, ± 1, ± 2, ± 3 … ), n – натуральное ( ℕ = 1, 2, 3, 4 … ).
Примеры рациональных чисел:
1 2 ; − 9 4 ; 0,3333 … = 1 3 ; 8 ; − 1236.
Примеры иррациональных чисел:
Аналогично, число 4 81 = 4 81 = 2 9 есть число рациональное.
В некоторых задачах требуется определить, какие из чисел являются рациональными, а какие иррациональными. Задание сводится к тому, чтобы понять, какие числа иррациональные, а какие под них маскируются. Для этого нужно уметь совершать операции вынесения множителя из-под знака квадратного корня и внесения множителя под знак корня.
Внесение и вынесение множителя за знак квадратного корня
При помощи вынесения множителя за знак квадратного корня можно ощутимо упростить некоторые математические выражения.
1 способ (вынесение множителя из-под знака корня): 2 8 2 = 2 4 ⋅ 2 2 = 2 4 ⋅ 2 2 = 2 ⋅ 2 = 4
2 способ (внесение множителя под знак корня): 2 8 2 = 2 2 8 2 = 4 ⋅ 8 2 = 4 ⋅ 8 2 = 16 = 4
Формулы сокращенного умножения (ФСУ)
(1) ( a + b ) 2 = a 2 + 2 a b + b 2
( 3 x + 4 y ) 2 = ( 3 x ) 2 + 2 ⋅ 3 x ⋅ 4 y + ( 4 y ) 2 = 9 x 2 + 24 x y + 16 y 2
(2) ( a − b ) 2 = a 2 − 2 a b + b 2
( 5 x − 2 y ) 2 = ( 5 x ) 2 − 2 ⋅ 5 x ⋅ 2 y + ( 2 y ) 2 = 25 x 2 − 20 x y + 4 y 2
Сумма квадратов не раскладывается на множители
(3) a 2 − b 2 = ( a − b ) ( a + b )
25 x 2 − 4 y 2 = ( 5 x ) 2 − ( 2 y ) 2 = ( 5 x − 2 y ) ( 5 x + 2 y )
(4) ( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
( x + 3 y ) 3 = ( x ) 3 + 3 ⋅ ( x ) 2 ⋅ ( 3 y ) + 3 ⋅ ( x ) ⋅ ( 3 y ) 2 + ( 3 y ) 3 = x 3 + 3 ⋅ x 2 ⋅ 3 y + 3 ⋅ x ⋅ 9 y 2 + 27 y 3 = x 3 + 9 x 2 y + 27 x y 2 + 27 y 3
(5) ( a − b ) 3 = a 3 − 3 a 2 b + 3 a b 2 − b 3
( x 2 − 2 y ) 3 = ( x 2 ) 3 − 3 ⋅ ( x 2 ) 2 ⋅ ( 2 y ) + 3 ⋅ ( x 2 ) ⋅ ( 2 y ) 2 − ( 2 y ) 3 = x 2 ⋅ 3 − 3 ⋅ x 2 ⋅ 2 ⋅ 2 y + 3 ⋅ x 2 ⋅ 4 y 2 − 8 y 3 = x 6 − 6 x 4 y + 12 x 2 y 2 − 8 y 3
(6) a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 )
8 + x 3 = 2 3 + x 3 = ( 2 + x ) ( 2 2 − 2 ⋅ x + x 2 ) = ( x + 2 ) ( 4 − 2 x + x 2 )
(7) a 3 − b 3 = ( a − b ) ( a 2 + a b + b 2 )
x 6 − 27 y 3 = ( x 2 ) 3 − ( 3 y ) 3 = ( x 2 − 3 y ) ( ( x 2 ) 2 + ( x 2 ) ( 3 y ) + ( 3 y ) 2 ) = ( x 2 − 3 y ) ( x 4 + 3 x 2 y + 9 y 2 )
Стандартный вид числа
Для того, чтобы понять, как приводить произвольное рациональное число к стандартному виду, надо знать, что такое первая значащая цифра числа.
Первой значащей цифрой числа называют его первую слева отличную от нуля цифру.
Для того, чтобы привести число к стандартному виду, надо:
Запятая сдвинулась влево на 1 разряд. Так как сдвиг запятой осуществляется влево, степень положительная.
Запятая сдвинулась вправо на 1 разряд. Так как сдвиг запятой осуществляется вправо, степень отрицательная.
Запятая сдвинулась вправо на три разряда. Так как сдвиг запятой осуществляется вправо, степень отрицательная.