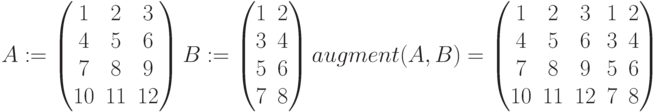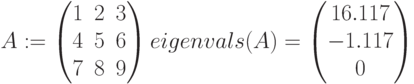Что такое встроенная функция mathcad
Что такое встроенная функция mathcad
Этот раздел описывает, как использовать команду Вставить функцию, чтобы увидеть список всех встроенных функций вместе с кратким описанием каждой функции. Набор встроенных функций Mathcad может изменяться, если Вы установили дополнительные функциональные пакеты или написали Ваши собственные встроенные функции. Функции могут появляться из четырех источников:
Встроенные функции Mathcad
Это — основной набор функций, которые поставляются с Mathcad. Все эти функции описаны в разных частях настоящего Руководства. Некоторые из них доступны только в Mathcad PLUS — если Mathcad PLUS не установлен, то некоторые функции, описанные в этом Руководстве, окажутся недоступными.
Пакеты Функций Mathcad.
Пакет Функций состоит из совокупности усовершенствованных функций, приспособленнных к специфической области применения. Описания этих функций содержатся в самом Пакете Функций. Список существующих Пакетов Функций постоянно расширяется и включает собрания функций для обработки изображения, численного анализа и продвинутого статистического анализа. Чтобы узнать больше относительно библиотеки Пакетов Функций, позвоните в MatSoft (USA) 8-101-617-577-1017. (В России консультации можно получить по 8-495-232-00-23, 8-495-126-90-65, 8-495-148-52-84).
Некоторые Электронные Книги содержат дополнительные функции. Описания этих функций находятся непосредственно в Электронных Книгах.
Функции, которые Вы записываете сами
Левый список диалогового окна “Вставить функцию” показывает все встроенные функции наряду с их аргументами. В окошке справа появляется описание выбранной функции. Чтобы применить функцию к уже введённому выражению, заключите выражение в синюю выделяющую рамку и вызовите функцию, как это описано выше.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Встроенные операторы и функции Mathcad
Таблица ПЗ.1. Арифметические операторы
Вычитание или отрицание (унарная операция)
Матричное умножение, умножение на скаляр
Скобки (изменение приоритета)
Возведение в степень n
Возведение матрицы в степень n
Скалярные операции над векторами и матрицами, если это не оговорено особо, производятся независимо над их каждым элементом, как над скаляром.
Таблица П3.2. Вычислительные операторы
Вычисление n-й производной
Сумма ранжированной переменной
Произведение ранжированной переменной
Таблица ПЗ.З. Встроенные функции по алфавиту
Обратная тригонометрическая или гиперболическая функция *
Функция Эйри первого рода
х,у — координаты точки
Угол между точкой и осью ОХ
file— строковое представление пути к файлу
Дозапись данных в существующий текстовый файл
z — аргумент функции
Аргумент комплексного числа
х,у — координаты точки
Угол, отсчитываемый от оси ОХ до точки (х,у)
А,В,С. — векторы или матрицы
Слияние матриц слева направо
n — порядок х — аргумент
Мнимая и действительная части функции Бесселя —Кельвина
Функция Эйри второго рода
х,у — векторы данных
и — вектор значений сшивок В-сплайнов
n — порядок полиномов
Вектор коэффициентов В-сплайна
Bulstoer (y0, t0, t1, M, D)
Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера
bulstoer (y0, t0, t1, acc, D, k, s)
Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера (для определения только последней точки интервала)
Bvalf it (z1, z2, x0, x1, xf, D, load1, load2, score)
zl,z2 — вектор начальных значений для недостающих левых и правых граничных условий
хО — левая граница xl — правая граница xf — внутренняя точка
D(x,y) — векторная функция, задающая систему ОДУ
Возвращает вектор недостающих граничных условий у краевой задачи для системы N ОДУ с дополнительным условием в промежуточной точке
Наименьшее целое, не меньшее х
Вектор прямого комплексного преобразования Фурье (в разных нормировках)
А — квадратная, определенная матрица
А — матрица или вектор
Объединение строковых переменных
А — квадратная матрица
Числа обусловленности в разных нормах (Ы, L2, Евклидова, »)
А — матрица i — индекс столбца
Сортировка строк матрицы по элементам 1-го столбца
CreateMesh (F, s0, s1, t0, t1, sgr, tgr, fmap)
tO.tl — пределы! sO.sl — пределы s
tgr, sgr — число точек сетки по t и s
fmap— функция преобразования координат
Cre-ateSpace(F[, t0, t1, tgr, fmap])
F(t) — векторная функция из трех элементов
tgr — число точек сетки по t
fmap— функция преобразования координат
Комплексный знак числа
х,у — векторы данных
Вектор коэффициентов кубического сплайна
r,6,z— цилиндрические координаты
Преобразование цилиндрических координат в прямоугольные
х— значение случайной величины
par — список параметров распределения *
Плотность вероятности со статистикой распределения *
Диагональная матрица, на диагонали которой находятся элементы вектора
А — квадратная матрица
Собственные значения матрицы
А — квадратная матрица
А. — собственное значение
Собственный вектор матрицы, соответствующий заданному собственному значению
А — квадратная матрица
Собственные векторы матрицы
Обратная функция ошибок
Возвращает строку S как сообщение об ошибке
Экспонента в степени z
x,y — векторы данных
g — вектор начальных значений а,Ь,с
Вектор прямого преобразования Фурье (в разных нормировках)
Функция Бесселя второго рода нулевого, первого и m-го порядка
n — порядок х — аргумент
Сферическая функция Бесселя второго рода
Некоторые функции, составляющие семейства типовых функций, приведены в сокращенном виде с недостающей частью имени в виде звездочки *. Например, различные статистические функции, описывающие различные распределения, или функции вывода в файлы. Подробные сведения содержатся в разделе, на который указывает соответствующая ссылка.
Встроенные функции MathCAD
Часто используемые функции
ceil(y) – возвращает наименьшее целое, большее или равное y. Значение y должно быть вещественным числом:
cols(A) – число столбцов матрицы А.
csort(B,n) – сортирует строки матрицы В таким образом, чтобы расположить элементы столбца n в порядке возрастания. Нумерация столбцов по умолчанию начинается с нуля:
eigenvals(A) – определяет вектор собственных значений для квадратной матрицы А:
find(x,y,…) – возвращает значения x,y,…, удовлетворяющие ограничениям: равенствам или неравенствам, заданным в блоке given решения уравнений. Число уравнений должно равняться числу неизвестных.
floor(y) – возвращает наибольшее целое, меньшее или равное y. Значение y должно быть вещественным числом:
identity(n) – создает единичную матрицу размером
length(v) – длина вектора v.
max(v) – максимальный по значению элемент вектора v.
min(v) – минимальный по значению элемент вектора v.
mean(M) – среднее арифметическое элементов вектора или матрицы.
median(v) – медиана вектора. Элементы вектора должны быть заданы в порядке возрастания:
rbeta (m, s 1, s2)Возвращает вектор m случайных чисел, имеющих бэта-распределение. 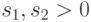
rgamma (m, s) Возвращает вектор m случайных чисел, имеющих гамма- распределение, 
rgeom (m, p) Возвращает вектор m случайных чисел, имеющих геометрическое распределение. 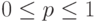
rlogis (m, l, s) Возвращает вектор m случайных чисел, имеющих логистическое распределение, в котором l является п а раметром расположения, а 
rpois (m,d) Возвращает вектор m случайных чисел, имеющих распределение Пуассона. 
rt (m, d) Возвращает вектор m случайных чисел, имеющих t-распределение Стьюдента. 
runif (m, a, b) Возвращает вектор m случайных чисел, имеющих равномерное распределение, в котором b и a являются граничными точками интервала. 
rnd (x) Возвращает равномерно распределенное случайное число между 0 и x. Эквивалент runif (1, 0, x).
round(y,n) – округляет вещественное число y до n знаков справа от десятичной точки. Если n отсутствует, то y округляется до ближайшего целого числа. Если n Нумерация строк по умолчанию начинается с нуля.
submatrix(M,ir,jr,ic,jc) – подматрица, состоящая из элементов матрицы М, содержащихся в строках от ir до jr и столбцах от ic до jc:
Что такое встроенная функция mathcad
Этот раздел описывает тригонометрические, гиперболические и показательные функции Mathcad вместе с обратными им. Здесь также описываются встроенные функции Бесселя.
Тригонометрические функции и обратные им.
Тригонометрические функции Mathcad и обратные им определены для любого комплексного аргумента. Они также возвращают комплексные значения везде, где необходимо. Результаты для комплексных значений вычисляются с использованием тождеств:
Для применения этих функций к каждому элементу вектора или матрицы используйте оператор векторизации.
Обратите внимание, что все эти тригонометрические функции используют аргумент, выраженный в радианах. Чтобы перейти к градусам, используется встроенная единица deg. Например, чтобы вычислить синус 45 градусов, введите sin(45*deg).
Имейте в виду, что из-за ошибок округления, свойственных машинной арифметике, Mathcad может возвращать очень большое число в той точке, где находится особенность вычисляемой функции. Вообще, необходимо быть осторожным при вычислениях в окрестности таких точек.
| asin(z) | Возвращает угол (в радианах), чей синус — z. |
| acos(z) | Возвращает угол (в радианах), чей косинус — z. |
| atan(z) | Возвращает угол (в радианах), чей тангенс — z. |
Гиперболические функции sinh и cosh определяются формулами:
Эти функции также могут использовать комплексный аргумент и возвращать комплексные значения. Гиперболические функции тесно связаны с тригонометрическими функциями. Справедливы формулы:
sinh(i


| sinh (z) | Возвращает гиперболический синус z. |
| cosh (z) | Возвращает гиперболический косинус z. |
| tanh (z) | Возвращает sinh(z)/cosh(z), гиперболический тангенс z. |
| csch (z) | Возвращает 1/sinh(z), гиперболический косеканс z. |
| sech (z) | Возвращает 1/cosh(z), гиперболический секанс z. |
| coth (z) | Возвращает 1/tanh(z), гиперболический котангенс z. |
| asinh (z) | Возвращает число, чей гиперболический синус — z. |
| acosh (z) | Возвращает число, чей гиперболический косинус — z. |
| atanh (z) | Возвращает число, чей гиперболический тангенс — z. |
Логарифмические и показательные функции
Логарифмические и показательные функции Mathcad могут использовать комплексный аргумент и возвращать комплексные значения. Значения экспоненциальной функции для комплексного аргумента вычисляются с применением формулы
e x+iy =e x (cos(y) + i
Вообще говоря, значения натурального логарифма даются формулой
ln(x + i





В Mathcad функция ln возвращает значение, соответствующее n = 0. А именно:
ln(x + i


Оно называется основным значением логарифма. Рисунок 1 иллюстрирует некоторые основные свойства логарифма.
| exp(z) | Возвращает e в степени z. |
| ln(z) | Возвращает натуральный логарифм z. (z 0). 0). |
| log(z) | Возвращает логарифм z по основанию 10. (z 0). 0). |
На Рисунке 1 показано, как можно использовать эти функции для вычисления логарифма по любому основанию.
Рисунок 1: Использование логарифмических функций.
Эти функции обычно возникают как решения для волнового уравнения, подчиненного цилиндрическим граничным условиям.
Функции Бесселя первого и второго рода, Jn(x) и Yn(x), являются решениями для дифференциального уравнения
Модифицированные функции Бесселя первого и второго рода, In(x) и Kn(x), являются решениями для немного видоизмененного уравнения:
| J0(x) | Возвращает J0(x); x вещественный. |
| J1(x) | Возвращает J1(x); x вещественный. |
| Jn(m, x) | Возвращает Jn(x); x вещественный, 0 m m 100. 100. |
| Y0(x) | Возвращает Y0(x); x вещественный, x > 0. |
| Y1(x) | Возвращает Y1(x); x вещественный, x > 0. |
| Yn(m, x) | Возвращает Yn(x). x > 0, 0 m m 100 100 |
| I0(x) | Возвращает I0(x); x вещественный. |
| I1(x) | Возвращает I1(x); x вещественный. |
| In(m, x) | Возвращает In(x); x вещественный, 0 m m 100. 100. |
| K0(x) | Возвращает K0(x); x вещественный, x > 0. |
| K1(x) | Возвращает K1(x); x вещественный, x > 0. |
| Kn(m, x) | Возвращает Kn(x). x > 0, 0 m m 100 100 |
Следующие функции возникают в широком круге задач.
x должен быть вещественным.
Гамма-функция Эйлера удовлетворяет рекуррентному соотношению
Откуда следует для положительных целых z:
Интеграл ошибок часто возникает в статистике. Он может также быть использован для определения дополнения интеграла ошибок по формуле:
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Что такое встроенная функция mathcad
Mathcad содержит функции для выполнения быстрого дискретного преобразования Фурье (БПФ) и его обращения. В Mathcad PLUS имеется также одномерное дискретное волновое преобразование и его обращение. Все эти функции имеют векторные аргументы. При определении вектора v для нахождения волнового преобразования или преобразования Фурье убедитесь, что первый элемент вектора имеет нулевой индекс: v0. Если элемент v0 не определен, Mathcad автоматически устанавливает его равным 0. Это может привести к искажению результата.
Введение в дискретное преобразование Фурье
В Mathcad входят два типа функций для дискретного преобразования Фурье: fft/ifft и cfft/icfft . Эти функции дискретны: они берут в качестве аргументов и возвращают векторы и матрицы. Они не могут быть использованы с другими функциями.
Используйте функции cfft и icfft во всех других случаях.
Первое условие необходимо, потому что функции fft/ifft используют тот факт, что для вещественных данных вторая половина преобразования Фурье является комплексно сопряженной с первой. Mathcad отбрасывает вторую половину вектора-результата. Это сохраняет и время и память при вычислениях.
Пара функций cfft/icfft не использует симметрию в преобразовании. По этой причине необходимо использовать их для комплексных данных. Так как вещественные числа — подмножество комплексных чисел, можно также использовать пару cfft/icfft для вещественных чисел.
Второе условие требуется, потому что пара функций fft/ifft использует высоко эффективный алгоритм быстрого преобразования Фурье. Для этого вектор аргумента, используемого с fft, должен иметь 2 m элементов. В функциях сfft/icfft использован алгоритм, который допускает в качестве аргументов как матрицы, так и векторы произвольного размера. Когда эта пара функций используется с матрицей в качестве аргумента, вычисляется двумерное преобразование Фурье.
Обратите внимание, что, если использована функция fft для прямого преобразования, необходимо использовать функцию ifft для обратного. Аналогично, если для прямого преобразования использована cfft, то для обратного необходимо использовать icfft.
Различные формулировки определения преобразования Фурье используют различные нормировочные коэффициенты и соглашения о знаке перед мнимой единицей в показателе экспоненты прямого и обратного преобразований. Функции fft, ifft, cfft и icfft используют 1/ 
Преобразование Фурье в вещественной области
Для вещественнозначных векторов с 2 m элементами можно применять пару функций fft/ifft. В алгоритме вычисления этих функций используются преимущества симметрии, существующей только для вещественных данных. Это позволяет сохранить и время, и память, необходимые для вычислений.
Элементы вектора, возвращаемого fft, вычисляются по формуле
В этой формуле n — число элементов в v, i — мнимая единица.
| ifft (v) | Возвращает обратное дискретное преобразование Фурье; результат — вещественнозначный. |
Аргумент v — вектор, подобный созданному функцией fft. Чтобы вычислить результат, Mathcad сначала создает новый вектор w, комплексно сопряженный v, и присоединяет его к вектору v. Затем Mathcad вычисляет вектор d, чьи элементы вычисляются по формуле:
Это та же самая формула, что и для fft, кроме знака минус в функции exp. Функции fft и ifft — точные обращения. Для всх вещественнозначных v справедливо ifft(fft(v))=v.
Преобразование Фурье в комплексной области
Комплексное преобразование Фурье требует следующих функций:
| cfft (A) | Возвращает дискретное преобразование Фурье комплекснозначных вектора или матрицы. Возвращаемый массив имеет тот же самый размер, что и массив, используемый как аргумент. |
| icfft (A) | Возвращается обращение дискретного преобразования Фурье вектора или матрицы данных. Функция icfft — обратная к функции cfft. Подобно cfft, эта функция возвращает массив того же самого размера, что и аргумент. |
Рисунок 3: Использование быстрых преобразований Фурье в Mathcad.
Пара преобразований cfft/icfft может работать с массивами любого размера. Однако они работают значительно быстрее, когда число строк и столбцов может быть представлено в виде произведения большого количества меньших сомножителей. Например, векторы с длиной 2 m относятся к этому классу, так же как и векторы, имеющие длины, подобные 100 или 120. С другой стороны, вектор, чья длина — большое простое число, замедлит вычисление преобразования Фурье.
Функции cfft и icfft — обратные друг к другу. То есть icfft(cfft(v))=v. Рисунок 3 показывает примеры использования преобразования Фурье в Mathcad.
Когда в качестве аргумента cfft используется матрица, результат есть двумерное преобразование Фурье исходной матрицы.
Альтернативные формы преобразования Фурье
Определения преобразования Фурье, обсужденные выше, не являются единственно возможными. Например, следующие определения для дискретного преобразования Фурье и его обращения можно найти в книге Ronald Bracewells, The Fourier Transform and Its Applications (McGraw-Hill, 1986):
Функции FFT, IFFT, CFFT и ICFFT используются аналогично функциям, обсужденным в предыдущем разделе.
Волновое преобразование
A Mathcad PLUS включены две функции волновых преобразований: для выполнения прямого одномерного дискретного волнового преобразования и его обращения. Преобразование выполняется с использованием четырехкоэффициентного волнового базиса Даубечи.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter