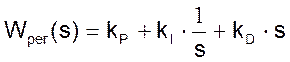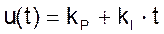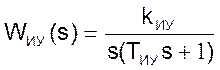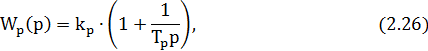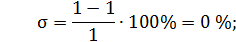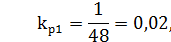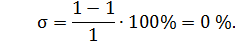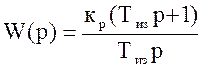Что такое время предварения

Мы при создании модели регулятора априори будем считать, что он работает в области нормальных режимов.

Наибольшее распространение получили регуляторы следующих типов:

■ I – интегральные регуляторы;

Передаточная функция PID регулятора имеет вид

Блок дифференцирования регулятора носит название «блок предварения».

PI регуляторы характеризуются параметром, который называется «время изодрома» (время удвоения входного сигнала).

При нулевых начальных условиях и действии на вход PI регулятора единичной функции выходной сигнал регулятора с течением времени будет изменяться по закону

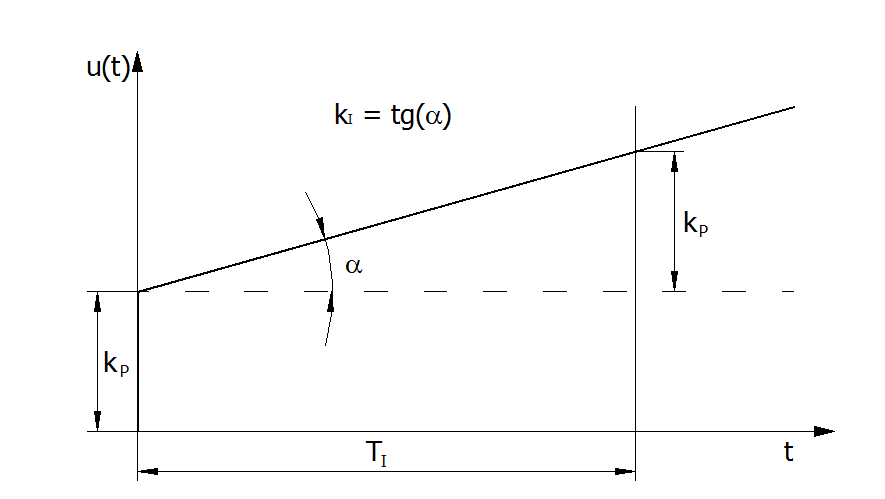
Время, в течение которого выходной сигнал u(t) станет равным 2k_P, и будет называться «временем изодрома» Т_I.

.

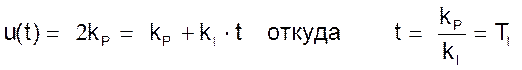
Из чертежа следует

Рис.1 Определение времени изодрома.

PID регулятор характеризуется помимо параметра «время изодрома» еще одним параметром «время предварения».

Время предварения равно

.

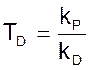
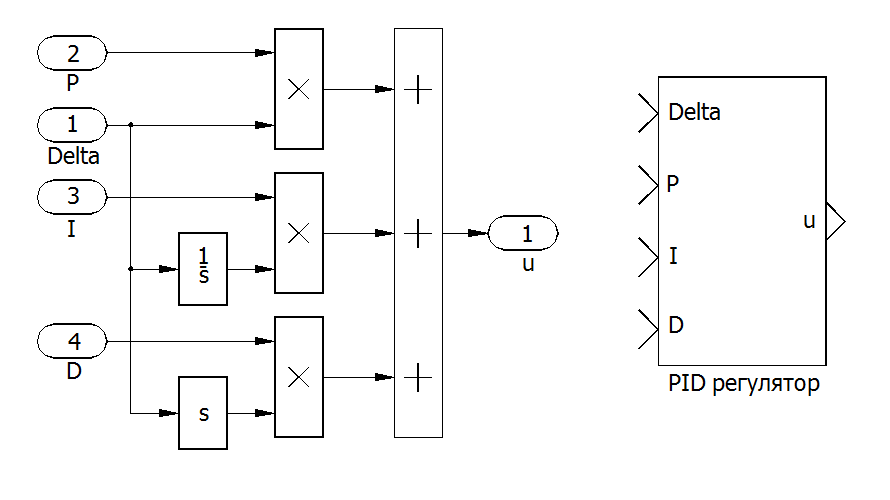
Модель регулятора в соответствии с его уравнением можно представить в виде:

Рис. 2. Модель PID регулятора в пиктограммах SIMULINK.

9.1.1.2. Качественные показатели систем автоматического управления промышленными объектами[1].

К основным качественным показателям систем автоматического управления промышленными объектами можно отнести:

2) перерегулирование – наибольшее отклонение регулируемого параметра от установившегося значения при внезапном изменении задания или под действием возмущающих сил;

3) динамический коэффициент регулирования – отношение максимального отклонения регулируемого параметра от величины заданного значения в переходном процессе, вызванное скачкообразным возмущением, к отклонению от задания при таком же возмущении, но без регулятора;

4) запас устойчивости – зависимость между изменениями каких либо параметров системы или характеристика, определяющая удаление годографа передаточной функции разомкнутой системы от критической точки;

5) степень устойчивости – абсолютное значение вещественной части корня характеристического уравнения, ближайшего к мнимой оси;

6) колебательность системы – тангенс половины угла, внутри и на границах которого расположены все корни характеристического уравнения;

7) максимальное ускорение, с которым изменяется регулируемая величина при заданном ступенчатом управляющем воздействии;

8) установившаяся погрешность регулирования – величина, характеризующая точность отработки задания регулирования в переходных и установившихся режимах;

9) интеграл квадрата отклонения регулируемой величины от ее заданного значения или интеграл квадрата отклонения регулируемой величины от заданного значения плюс сумма некоторого числа производных этого отклонения в квадрате;

10) среднеквадратическое значение отклонения регулируемой величины от заданного значения при случайном характере возмущений;

11) наименьшая возможная длительность отработки начального отклонения (оптимальность по быстродействию);

12) наименьшее возможное перерегулирование (оптимальность по перерегулированию);

13) среднеквадратическое значение отклонения регулируемой величины от заданного значения плюс интеграл от квадрата отклонения или показатели, характеризующие процессы при отработке начального отклонения;

14) максимально допустимые значения амплитуды и частоты автоколебаний регулируемого параметра.

Для систем взаимосвязанного регулирования имеются дополнительные показатели: автономность или инвариантность одних регулируемых параметров к возмущениям, действующим в контурах регулирования других параметров.

При каскадном включении регуляторов когда один регулятор (ведущий) «ведет» другие (ведомые) показателем может быть определенное соотношение скоростей протекания переходных процессов и заданная точность.

Даже далеко не полный перечень качественных характеристик автоматического регулирования показывает, что удовлетворить всем требованиям да еще одновременно просто невозможно, более того некоторые из них являются взаимно противоречивыми. Естественно предложить выбрать несколько из них в качестве основных, а остальные считать второстепенными и не предъявлять к ним особых требований. При таком разделении следует руководствоваться требованиями технологического процесса.

9.1.2. Области применения регуляторов разных типов.

9.1.2.1. Пропорционально регуляторы (рекомендации по их применению)[2].

Пропорциональный регулятор, включенный последовательно с астатическим исполнительным устройством типа

относится к интегральным регуляторам.

9.1.2.2. Интегральные регуляторы (рекомендации по их применению).

Интегральные регуляторы не могут обеспечить устойчивости нейтральных объектов и объектов с отрицательным самовыравниванием без запаздывания и с запаздыванием, так как такие объекты структурно не устойчивы[4].

9.1.2.3. Пропорционально-дифференциальные регуляторы (рекомендации по их применению).

Применение PD регуляторов дает возможность увеличивать общее усиление при сохранении устойчивости системы, что резко улучшает качество переходных процессов.

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Расчёт настроек регулятора и его выбор

Передаточная функция ПИ-регулятора W_p(p) имеет вид, соответствующий формуле (2.26):

где k_п, k_и – коэффициенты пропорциональной и интегральной частей;

Т_и и Т_из – постоянные времени интегрирования и изодрома;

p – символ дифференцирования.

Для упрощенной типовой модели первого порядка с запаздыванием настроечные параметры регулятора принимают вид в соответствии с формулами (2.27), (2.28):

(2.27)

где k_p – коэффициент пропорциональной части;

k_о – коэффициент передачи объекта;

τ_о – время запаздывания;

Т_и – постоянная времени интегрирования;

Т_о – постоянная времени.

0,0091,

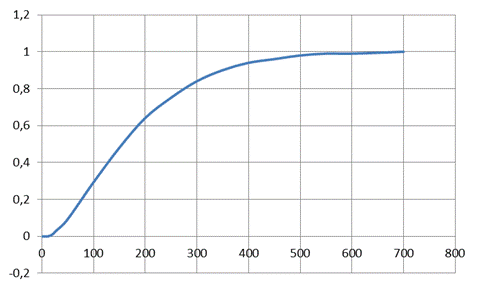
Рисунок 2.19 – Переходный процесс ПИ-регулятора с настроечными параметрами

По переходному процессу определяются следующие показатели качества [6]:

– используя формулу (2.29), рассчитывается величина перерегулирования :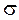

%, (2.29)

где y_м – величина отклонения;

– установившееся состояние.

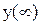
– длительность переходного процесса t_п определяется по графику, изображённому на рисунке 2.19, t_п = 628 с;

– количество колебаний n определяется по графику (рисунок 2.19), n = 0;

– коэффициент затухания рассчитывается по формуле 2.30:

%, (2.30)

где А₁ и А₂ – соседние амплитуды колебаний выходного сигнала одного знака.

Передаточная функция ПИД-регулятора W_p(p) имеет вид, соответствующий формуле (2.31):

, (2.31)

где k_п, k_и – коэффициенты пропорциональной и интегральной частей;

Т_и и Т_из – постоянные времени интегрирования и изодрома;

Т_д – время предварения;

p – символ дифференцирования.

Для упрощенной типовой модели с запаздыванием настроечные параметры регулятора принимают вид в соответствии с формулами (2.32), (2.33), (2.34):

где k_p – коэффициент пропорциональной части;

k_о – коэффициент передачи объекта;

τ_о – время запаздывания;

Т_и – постоянная времени интегрирования;

Т_о – постоянная времени;

Т_д – время предварения.

Используя формулы (2.35), (2.36), рассчитываются коэффициенты передачи объекта k_р1, k_р2:

где Т_и – постоянная времени интегрирования;

k_p – коэффициент пропорциональной части.

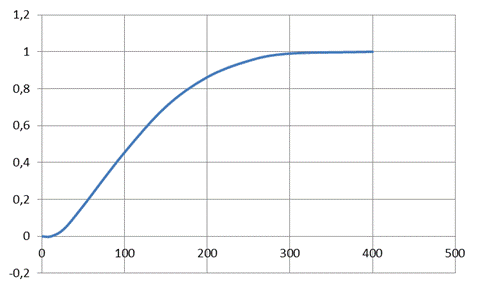
Полученный переходный процесс является неустановившимся, поэтому значения k_р, k_р1, k_р2 подбираются таким образом, чтобы переходный процесс установился полностью (рисунок 2.20).

Принимаются следующие значения коэффициентов передачи объекта k_р, k_р1 и k_р2:

Рисунок 2.20 – Переходный процесс ПИД-регулятора с расчетными параметрами

По переходному процессу определяются следующие показатели качества [7]:

– используя формулу (2.29), рассчитывается величина перерегулирования :

– длительность переходного процесса t_п определяется по графику, изображённому на рисунке 2.20, t_п = 319 с;

– количество колебаний n определяется по графику (рисунок 2.20), n = 0;

– коэффициент затухания рассчитывается по формуле 2.30:

Выбор регулятора производится по прямым и по частотным показателям качества.

Источник

Пропорционально-интегральный регулятор

.

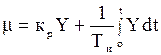
Передаточная функция ПИ-регулятора: W(p) = к_р + 1 /(Т_ир).

При постоянном входном сигнале Y=Y_o уравнение регулятора можно представить в виде:

Кроме рассмотренной структурной схемы ПИ-регулятора на практике широко применяется следующая схема:

которая реализует закон регулирования вида:

Передаточная функция регулятора имеет вид:

Временная характеристика такого регулятора имеет вид:

Дифференциальные регуляторы (Д, ПД, ПИД)

Реально такие регуляторы бывают двух видов : пропорционально-дифференциальные (ПД-) и пропорционально-интегрально-дифференциальные (ПИД-) регуляторы. Дифференциальные регуляторы еще называют регуляторами с предварением.

— ПД-регулятор

Вид передаточных функций регуляторов:

Временные характеристики регуляторов:

регулятора на линейно нарастающий входной сигнал:

Источник

время предварения

1 derivative action time

время предварения
время дифференцирования
Время, в течение которого входной сигнал, изменяющийся с постоянной скоростью, достигнет значения выходного сигнала, изменяющегося с той же скоростью, в момент начала отсчета.
[ ГОСТ 9988-84]

derivative action time
for a derivative element the same as the derivative action coefficient, if its input and output variables have the same unit
Note 1 – Then the derivative action time is given by T_D = K_D, where K_D is the derivative action coefficient.
Note 2 – The derivative action time can also be given as the duration of the time interval that a rampwise variation of the input variable needs to reach the same value as the stepwise varying output variable.
[IEV ref 351-28-26]

constante de temps de dérivation
pour un élément à action par dérivation, la constante de temps de dérivation est égale au coefficient d’action par dérivation, si ses variables d’entrée et de sortie sont dans la même unité
Note 1 – La constante de temps de dérivation est alors donnée par T_D = K_D, où K_D est le coefficient d’action par dérivation.
Note 2 – La constante de temps de dérivation peut également être donnée comme la durée de l’intervalle de temps nécessaire pour qu’une variation en rampe de la variable d’entrée atteigne la même valeur que la variable de sortie correspondante.
[IEV ref 351-28-26]

Источник

Форум АСУТП

Клуб специалистов в области промышленной автоматизации

Запутался в определениях. Помогите разобраться

Запутался в определениях. Помогите разобраться

Сообщение littlemaster1 » 29 мар 2016, 21:48

Запутался в определениях. Помогите разобраться

Сообщение rwg » 29 мар 2016, 22:37

Стыдно признаться, но из трёх вопросов могу ответить только на один. Настройка по методу Зиглера-Николса производится для любого ПИ и ПИД регулятора, как бы он ни назывался. Лишь бы он был ПИ(Д). Слово «изодром» когда то очень давно я слышал, скорей всего применительно к пневматическим регуляторам. А с параллельными никаких ассоциаций.

Запутался в определениях. Помогите разобраться

Сообщение Serex » 29 мар 2016, 23:36

Запутался в определениях. Помогите разобраться

Сообщение rwg » 30 мар 2016, 00:36

Запутался в определениях. Помогите разобраться

Сообщение littlemaster1 » 30 мар 2016, 06:54

Запутался в определениях. Помогите разобраться

Сообщение rwg » 30 мар 2016, 08:09

Запутался в определениях. Помогите разобраться

Сообщение VADR » 30 мар 2016, 08:25

Запутался в определениях. Помогите разобраться

Сообщение Looker » 30 мар 2016, 12:50

Запутался в определениях. Помогите разобраться

Сообщение perfect_gentleman » 30 мар 2016, 13:40

Запутался в определениях. Помогите разобраться

Сообщение rwg » 30 мар 2016, 13:43

Запутался в определениях. Помогите разобраться

Сообщение Serex » 30 мар 2016, 14:33

Запутался в определениях. Помогите разобраться

Сообщение perfect_gentleman » 30 мар 2016, 15:24

Запутался в определениях. Помогите разобраться

Сообщение rwg » 30 мар 2016, 16:00

Запутался в определениях. Помогите разобраться

Сообщение VADR » 30 мар 2016, 16:10

Запутался в определениях. Помогите разобраться

Сообщение perfect_gentleman » 30 мар 2016, 16:25

Запутался в определениях. Помогите разобраться

Сообщение Looker » 30 мар 2016, 16:45

Запутался в определениях. Помогите разобраться

Сообщение littlemaster1 » 30 мар 2016, 17:43

Что означает «series form» в этом тексте?: Almost all analog controllers and most commercial digital control systems use the series form. Such tuning methods as the Ziegler-Nichols methods (discussed in Chapter 6 ) were developed using series form controllers.

Хочу ещё добавить, что смоделировал в симулинке параллельный пи-регулятор (сумма пропорциональной и интегральной части) с параметрами, рассчитанными по зиглеру-николсу. Получился переходный процесс с параметрами перерегулирования = 20% и временем регулирования 176 сек. При самой малой постоянной времени объекта 10 сек.
Есть ли у системы с параметрами по зиглеру-николсу стандартные прямые показатели, как при настройке на модульный оптимум, например?

Источник