Что такое внешнее касание окружностей
Две окружности на плоскости.
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
 | ||
| Внешнее касание двух окружностей | ||
 | ||
| Внутреннее касание двух окружностей | ||
 | ||
| Окружности пересекаются в двух точках | ||
 | ||
 | ||
| Каждая из окружностей лежит вне другой | ||
 Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
 Расстояние между центрами окружностей равно сумме их радиусов Расстояние между центрами окружностей равно разности их радиусов | ||
| Окружности пересекаются в двух точках | ||
 Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
 | |
| Внутреннее касание двух окружностей | |
 | |
| Окружности пересекаются в двух точках | |
 | |
| Внешнее касание двух окружностей | |
 | |
 | |
| Каждая из окружностей лежит вне другой | |
 | |
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Существует единственная общая внешняя касательная. Других общих касательных нет.
Существуют две общих внешних касательных. Других общих касательных нет.
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет













































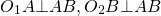
 2) Если две окружности с различными радиусами касаются внешне, то общие внешние касательные образуют угол, в который обе окружности вписаны.
2) Если две окружности с различными радиусами касаются внешне, то общие внешние касательные образуют угол, в который обе окружности вписаны.




 — расстояние между центрами окружностей радиусов
— расстояние между центрами окружностей радиусов  и
и  общая внешняя касательная касается окружностей в точках
общая внешняя касательная касается окружностей в точках  и
и  общая внутренняя в точках
общая внутренняя в точках  и
и  то
то


 .
. .
.

 .
.
 . Значит, SO || O 2 Y и
. Значит, SO || O 2 Y и  .
.