Что такое вес графа
Что такое вес графа
страницы: 1 2 3 4
Содержание
Ориентированные графы
Рис. 11.6. Орграф
Таблица 11.2. Примеры ориентированных графов
Взвешенные графы
Рис. 11.7. Взвешенный граф
Таблица 11.3. Примеры взвешенных графов
| Граф | Вершины | Вес вершины | Рёбра (дуги) | Вес ребра (дуги) |
|---|---|---|---|---|
| Таможни | Государства | Площадь территории | Наличие наземной границы | Стоимость получения визы |
| Переезды | Города | Стоимость ночёвки в гостинице | Дороги | Длина дороги |
| Супер–чайнворд | Слова | — | Совпадение конца и начала слов (возможность «сцепить» слова) | Длина пересекающихся частей |
| Карта | Государства | Цвет на карте | Наличие общей границы | — |
| Сеть | Компьютеры | — | Сетевой кабель | Стоимость кабеля |
Способы представления графов
Матрица смежности
Матрица смежности Sm — это квадратная матрица размером NxN ( N — количество вершин в графе ), заполненная единицами и нулями по следующему правилу:
Заметим, что данное определение подходит как ориентированным, так и неориентированным графам : матрица смежности для неориентированного графа будет симметричной относительно своей главной диагонали, а для орграфа — несимметричной.
Задать взвешенный граф при помощи матрицы смежности тоже возможно. Необходимо лишь внести небольшое изменение в определение:
Таблица 11.8. Примеры матриц смежности
| a | b | c | d | f | 1 | 2 | 3 | 4 | 5 | a | b | c | d | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | a | 0 | 1 | 10 | 0 |
| b | 1 | 0 | 1 | 1 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | b | 1 | 0 | 2 | 10 |
| c | 1 | 1 | 0 | 1 | 1 | 3 | 1 | 1 | 0 | 0 | 1 | c | 10 | 2 | 0 | 3 |
| d | 0 | 1 | 1 | 0 | 1 | 4 | 0 | 0 | 1 | 0 | 0 | d | 0 | 10 | 3 | 0 |
| f | 0 | 1 | 1 | 1 | 0 | 5 | 0 | 0 | 0 | 0 | 0 |
Что такое взвешенный граф в информатике
Вы будете перенаправлены на Автор24
Взвешенный граф в информатике — это граф с вершинами или рёбрами, несущими добавочную информацию, другими словами вес.
Взвешенный граф
Под взвешенным графом понимается граф, у которого рёбрам соответствуют некоторые весовые параметры. То есть каждому ребру (дуге) поставлено в соответствие некое числовое значение, которое называется длина дуги (или вес, стоимость). Обычные графы (не взвешенные) тоже возможно представить в виде взвешенных, если считать, что все их рёбра обладают весом равным единице. Под длиной пути во взвешенном графе понимается суммарная длина (вес) рёбер, составляющих данный путь. Расстоянием между вершинами считается дистанция самого короткого по весу пути. На рисунке один приведён пример взвешенного графа и там можно видеть, что расстояние между вершинами a и d равняется шести. То есть это путь с наименьшим суммарным весом (от вершины a и далее b, c, d).
Рисунок 1. Образец взвешенного графа. Автор24 — интернет-биржа студенческих работ
Эйлеровы и гамильтоновы графы
Если в составе графа есть цикл (возможно и не простой), который содержит каждое ребро графа один раз, то этот цикл носит название эйлеровый цикл, и, соответственно, такой граф именуется эйлеровым.
Если в составе графа существует цепь, которая содержит каждую вершину один раз, то эта цепь считается эйлеровой цепью, а граф называется полуэйлеровым.
Эти формулировки появились в 1735-ом году в работе Эйлера, где он искал решение задачи о Кёнигсбергских мостах и там первым привёл термин граф. На рисунке два изображена схема, где представлены семь мостов в городе Кёнигсберг (сегодня это Калининград). По условиям задачи требуется пересечь каждый из мостов только один раз и выполнить возврат в начальную точку С. Так как обход мостов завешается в начальной точке маршрута и есть условие однократного пересечения каждого моста, то такой маршрут можно считать простым циклом, который содержит все рёбра графа. Позже подобные циклы получили название эйлеровых, а графы, в составе которых есть такие циклы, назвали эйлеровыми графами.
Готовые работы на аналогичную тему
Рисунок 2. Задача Эйлера о Кёнигсбергских мостах. Автор24 — интернет-биржа студенческих работ
На этом рисунке а — схема местоположения семи мостов в Кёнигсберге (сегодня Калининграде); б — граф, изображающий семь мостов в Кёнигсберге. Мосты представляют собой ребра графа, вершины отображают районы города, которые соединяют мосты.
Цикл Эйлера возможно представить как след от пера, которое рисует данный граф без отрыва пера от листа. То есть, иначе говоря, эйлеровы графы представляют собой графы, которые возможно нарисовать одним движением пера. При этом сам процесс рисования имеет начало и окончание в одной точке.
Выяснив, что в этом графе нет циклических обходов, которые проходят по каждому ребру один раз, Эйлер решил поставить задачу в более общей формулировке: какие должны выполняться условия, чтобы такой цикл в графе мог быть обнаружен? Ответ на поставленный вопрос Эйлер дал в своей теореме. Теорема Эйлера: для существования в связанном неориентированном графе G эйлерова цикла, необходимо и достаточно, чтобы количество вершин с нечётной степенью не превышало две.
Цепью Гамильтона в графе считается простая цепь, проходящая через каждую вершину графа строго по одному разу. Цикл графа, который проходит через все его вершины, считается гамильтоновым циклом. Гамильтоновым называют граф, у которого есть гамильтонов цикл. Гамильтоновы графы возможно использовать для построения моделей большого числа задач практики. К примеру, такие графы могут моделировать движение поездов, и это поможет составить оптимальное расписание их движения. Базой подобных задач является классическая проблема коммивояжера, которому необходимо выполнить вояж по городам и возвратиться в исходную точку, посетив каждый город только один раз. Затраты на поездку должны быть минимальными.
Погружение в графы
Графы в большинстве своем представляют собой неупорядоченные деревья. В основном это утверждение касается ненаправленных и невзвешенных графов. Однако оно остается в силе и в отношении направленных или взвешенных графов, либо направленных и взвешенных одновременно, только при этом надо детализировать понятие “неупорядоченности”.
Направленные графы
Прежде, чем познакомиться с направленным графом, взгляните на ненаправленный граф, представленный ниже:
Ненаправленный граф позволяет свободно перемещаться между вершинами в любом направлении. Теперь посмотрите на направленную версию этого графа:
Тут все меняется. Вы можете перемещаться между вершинами только в направлении стрелки, прикрепленной к каждому ребру. Например, вы можете перейти из пункта А в пункт В, но не из пункта В в пункт А. Немного более строго, верно?
Взвешенные графы
Теперь подумаем о том, чтобы добавить веса ребрам графа. Представьте себе, что у каждого ребра есть цена; цена, которую нужно заплатить, чтобы пересечь ребро. Но перед этим представьте, что все ребра бесплатные, то есть имеют нулевую цену.
На самом деле это мало что меняет, так как с самого начала не было никакой цены, которую нужно было платить. Мы все еще можем пройти по графу без раздумий, если будем следовать указаниям стрелок. Даже если у каждого ребра есть цена, пока все они равны, поскольку каждое ребро имеет одинаковое значение, или вес.
Хорошо, но что, если бы цены были другими? Как бы это изменило способ прохождения по графу?
Поскольку цены теперь отличаются друг от друга, вводится новая динамика. Переход от вершины к вершине будет стоить разных сумм “денег”. Иногда есть только один путь, но в некоторых случаях можно выбрать маршрут, и цена обычно служит определяющим фактором в этом решении. В общем, при переходе из одной вершины графа в другую “самый дешевый” путь является желаемым. Например, если бы я хотел выбрать самый дешевый путь из пункта А в пункт Е, я бы пошел по маршруту АBDЕ. Хотя первоначальным решением мог бы стать маршрут ABE, на самом деле он вышел бы дороже. Подсчеты показывают: стоимость ABE составляет 11, в то время как АBDЕ — всего 9. Надеюсь, вы получили основное представление о взвешенных графах.
До этого момента я называл числа, представляющие каждое ребро, его “ценой”, имея в виду деньги. На самом деле эти цифры обозначают “вес” ребра. Аналогия с деньгами упрощает знакомство с этим видом графа, поскольку деньги — это то, с чем все мы знакомы. Есть и другие способы рассмотрения взвешенного графа. Вы можете представить числа как расстояние между двумя вершинами. Большинство иллюстраций графов не соотнеслись бы с таким представлением, но, тем не менее, такая аналогия тоже приемлема.
Представление графов в коде
Итак, вы уже знаете, что такое направленные и взвешенные графы. Теперь выясним, как представить графы в коде. До сих пор мы использовали только иллюстрации графов. Что ж, оказывается, существует множество способов их представления в коде. Рассмотрим некоторые из них в отношении направленного и невзвешенного графа, показанного ранее.
Список ребер
Список ребер — это именно то, на что похож приведенный ниже код; это список всех ребер на графе. Обратите внимание: каждое ребро представлено своими вершинами — начальной и конечной.
Список смежности
Список смежности — это что-то вроде словаря, в котором каждый ключ является вершиной в графе, а каждое значение — это все, к чему эта вершина примыкает. В направленном графе стрелки должны быть направлены так, чтобы вершина была ключом в списке.
Матрица смежности
Чтобы лучше понять матрицу смежности, изобразим ее в виде рисунка. Если у вас есть опыт работы с матрицами в исчислении, то вам это дастся довольно легко. Если нет, не стоит беспокоиться — всему свое время.
В матрице смежности “0” означает, что две вершины не являются смежными, а “1”, указывает на то, что они являются смежными. Существует множество способов манипулировать такой матрицей и работать с ней, но это выходит за рамки данного объяснения. Обратите внимание на то, что на диагонали есть только нули. Подумайте, почему это так…
Для кодирования матрицы смежности существует несколько способов. В следующих случаях используется ООП:
Когда следует использовать каждый метод
Каждый метод является допустимым представлением графа. Когда же предпочесть один из них всем остальным? Если коротко, то это зависит от того, что вы делаете и как собираетесь манипулировать данными. Например, матрица смежности великолепна и проста в использовании, но может занимать гораздо больше памяти, чем, скажем, список ребер. Обратите внимание и на то, что каждый метод годится для указания веса ребра в случае со взвешенным графом; эта информация была исключена из примеров для упрощения.
Заключение
Мир графов в компьютерных науках огромен. Возможно, для вас это было первое знакомство с ним. Надеемся, что теперь вы лучше сможете понять основы продвижения проектов.
Для дальнейшего погружения в тему рекомендуем изучить алгоритмы обхода, такие как DFS (поиск в глубину) и BFS (поиск в ширину).
Содержание урока
Взвешенный граф
Взвешенный граф
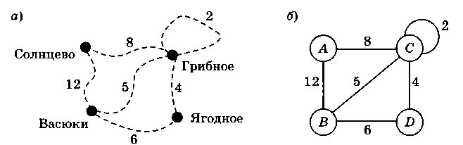
Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).

Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.
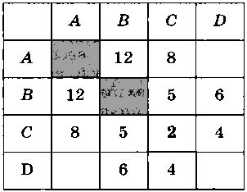
Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.
Что означают пустые ячейки в весовой матрице?
Как по весовой матрице сразу определить, сколько рёбер в графе?
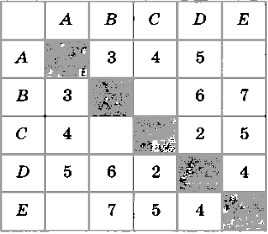
Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?
Следующая страница 
Cкачать материалы урока
Лекция 11. Графы
Геометрические графы
Глава о графах начиналась с рассказа о неких рисунках и схемах, которые Д. Кёниг предложил называть графами. Тем не менее, в предыдущем пункте, где давались определения понятия графа, рисунки или схемы даже не упоминались. Дело в том, что выше речь шла о так называемых абстрактных графах, а рисунки и схемы представляют собой геометрические графы. Эти два понятия хотя и очень близкие, но, тем не менее, различные.
1. каждая замкнутая кривая множества 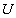
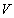
2. каждая незамкнутая кривая множества 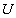
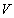
3. кривые множества 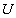
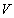
Таким образом, геометрический граф есть просто геометрическая конфигурация или структура в пространстве, состоящая из множества точек, взаимосвязанных множеством простых (не имеющих точек самопересечения) кривых. На рис. 4.1 изображены два геометрических графа.
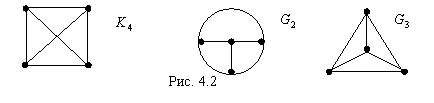
Очевидно, что вершины любого абстрактного графа можно представить точками пространства, а его ребра отождествить с некоторыми простыми кривыми, соединяющими концы этих ребер. Поэтому любой абстрактный граф всегда эквивалентен (по отношению к свойствам, изучаемым в теории графов) некоторому геометрическому графу. Геометрический граф, эквивалентный в указанном выше смысле абстрактному графу, будем называть изображением этого абстрактного графа. Таким образом, геометрические графы можно рассматривать как удобное и наглядное представление абстрактных графов, а не просто как частный случай. Отметим только, что существует огромное количество вариантов расположения вершин геометрического графа в пространстве и не меньшее количество способов начертания его ребер. Следовательно, у абстрактного графа могут быть различные по виду изображения, на первый взгляд совершенно не похожие друг на друга. Оба графа на рис.4.1 являются изображениями абстрактного графа из примера 4.1. Не похожи и три изображения абстрактного графа, показанные на рис. 4.2.

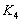
Хотя многие графы, представляющие реальные объекты, являются геометрическими графами, с точки зрения теории графов их единственная структурная особенность состоит в том, что с каждым геометрическим ребром связаны две (возможно, совпадающие) геометрические вершины. Теория графов построена с учетом именно этой особенности и не учитывает реальной природы вершин и ребер. Таким образом, нумерация вершин и ребер с фиксацией вершин концов каждого ребра и указанием его ориентации (в тех случаях, когда это необходимо) содержит всю информацию, достаточную для описания и геометрического графа, и абстрактного графа. Все понятия и определения, введенные выше для абстрактных графов, справедливы и для их изображений, т.е. для геометрических графов.
Заметим, что введение абстрактного графа позволяет не только избавиться от случайных геометрических характеристик, сохранив наиболее существенные комбинаторные свойства графа. Оно расширяет возможности приложения теории, так как многие реальные структуры имеют комбинаторные свойства, которые удобно рассматривать как граф. Например, в виде графа можно задать соотношения между отдельными работами, которые составляют сложные проекты. В этом случае ребра, после того как задана их ориентация, представляют отдельные работы, а вершины отражают последовательность их выполнения.
Взвешенные графы
Следующий шаг в описании связей между объектами с помощью графов состоит в приписывании ребрам некоторых количественных значений, качественных признаков или характерных свойств, называемых весами. В простейших случаях это может быть порядковая нумерация ребер, указывающая на очередность их рассмотрения (приоритет или иерархия). Вес ребра может означать длину (пути сообщения), пропускную способность (линии связи), напряжение или ток (электрические цепи), количество набранных очков (турниры), валентность связей (химические формулы), количество рядов движения (автомобильные дороги), цвет проводника (монтажные схемы электронного устройства), характер отношения между людьми (сын, отец, подчиненный, учитель) и т. п.
Вес можно приписывать не только ребрам, но и вершинам. Например, вершины, соответствующие населенным пунктам, могут характеризоваться количеством мест в гостиницах, пропускной способностью станций техобслуживания. Вообще, вес вершины означает любую характеристику соответствующего ей объекта – атомный вес элемента в структурной формуле, цвет изображаемого вершиной предмета, возраст человека и т. п.
Определение 4.4. Графы, вершинам и (или) ребрам которых приписаны некоторые веса, называют взвешенными графами. Графы, вершины которых пронумерованы, еще называют помеченными графами.
Особое значение для моделирования физических систем приобрели взвешенные ориентированные графы, называемые графами потоков сигналов или сигнальными графами. Вершины сигнального графа отождествляются с некоторыми переменными, описывающими состояние системы, а вес каждой вершины означает функцию времени или некоторой величины, характеризующую соответствующую переменную (сигнал вершины). Дуги отображают связи между переменными, и вес каждой дуги представляет собой численное или функциональное отношение, задающее передачу сигнала от одной вершины к другой (передача дуги). Сигнальные графы находят широкое применение в теории цепей и систем, а также во многих других областях науки и техники.
Степени вершин
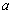
Число 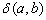
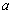
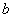
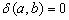
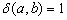
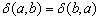
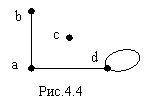
У графа, представленного на рис. 4.4, 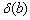
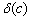
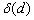
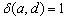
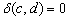
Выпишем несколько простых формул. Очевидно, что степень любой вершины графа 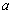
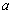
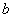
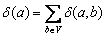
Так как каждое звена графа принимается во внимание при вычислении степеней обоих его концов, то число звеньев графа 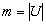
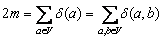
Эти формулы справедливы и при наличии у графа петель, если только при подсчете степеней вершин петли считать дважды. Из последней формулы следует, что сумма степеней всех вершин неографа всегда четна, следовательно,
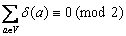
Сумма в левой части этой формулы, естественно, останется четной даже в том случае, когда отбрасываются все четные степени вершин. Поэтому справедлива следующая теорема.
Это утверждение установлено Эйлером и является исторически первой теоремой теории графов.