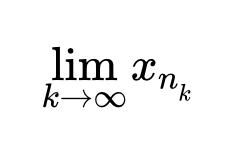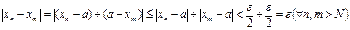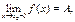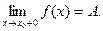Что такое верхний предел

Верхний предел

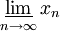
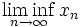
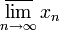
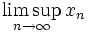
Нижним пределом последовательности (обозначается или ) называется наименьший элемент множества частичных пределов последовательности, а верхним пределом ( или ) — наибольший элемент.

Докажем это утверждение для верхнего предела. По теореме Больцано — Вейерштрасса множество частичных пределов ограниченной последовательности непусто. Пусть s — верхняя грань множества A частичных пределов. Тогда заметим, что 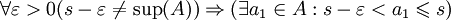, а это означает, что в любой окрестности точки a₁ находится бесконечно много членов последовательности. Поскольку утверждение верно для любого , мы можем сказать, что в любой окрестности точки s содержится бесконечно много членов последовательности (так как в любой окрестности мы можем найти точку a₁ ). Значит, s по определению является предельной точкой последовательности, а стало быть, и её частичным пределом, что и требовалось доказать. Аналогично доказывается случай нижнего предела.

Последовательность <x_n> сходится к a тогда и только тогда, когда 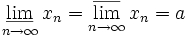, так как получается, что a — единственная предельная точка множества элементов последовательности.

Полезное

Смотреть что такое «Верхний предел» в других словарях:

верхний предел — Пороговое значение [http://www.dunwoodypress.com/148/PDF/Biotech Eng Rus.pdf] Тематики биотехнологии EN ceiling limit … Справочник технического переводчика

верхний предел — viršutinė riba statusas T sritis automatika atitikmenys: angl. super limit; superior limit vok. obere Grenze, f; oberer Grenzwert, m; Obergrenze, f rus. верхний предел, m pranc. limite supérieure, f … Automatikos terminų žodynas

верхний предел — viršutinė riba statusas T sritis fizika atitikmenys: angl. superior limit; upper limit vok. obere Grenze, f; oberer Grenzwert, m rus. верхний предел, m; верхняя граница, f pranc. limite supérieure, f … Fizikos terminų žodynas

верхний предел измерений тензорезисторного датчика силы — верхний предел измерений датчика Значение измеряемой силы, соответствующее верхней границе измерений тензорезисторного датчика силы, для которого нормированы допускаемые погрешности. [ГОСТ 16217 83] Тематики датчики и преобразователи физических… … Справочник технического переводчика

верхний предел критической температуры фазового перехода или превращения — верхний предел критической точки фазового перехода или превращения — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом Синонимы верхний предел критической точки фазового перехода или превращения EN… … Справочник технического переводчика

Верхний предел воспламенения — максимальная концентрация вещества в паровом облаке, при которой еще возможно инициирование самоподдерживающейся реакции горения. При концентрации выше В. п. в. реакция горения уже невозможна … Российская энциклопедия по охране труда

верхний предел воспламеняемости — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN upper flammable limitUFL … Справочник технического переводчика

верхний предел для передачи значений измеряемой величины. — верхний предел для передачи значений измеряемой величины. — [ГОСТ Р МЭК 60870 5 104 2004] Тематики телемеханика, телеметрия EN high limit for transmission of measured value … Справочник технического переводчика

верхний предел измерений — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN full scale value … Справочник технического переводчика

верхний предел измерений (прибора) — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN full scale value … Справочник технического переводчика

Источник

Подпоследовательности и частичные пределы последовательностей

Определение подпоследовательности

Свойства подпоследовательностей

Свойство 3 является следствием свойств 1 и 2.

Частичный предел последовательности

Произвольная последовательность может иметь конечное или бесконечное число частичных пределов ⇑.

5. Свойство частичного предела последовательности
Точка является частичным пределом последовательности тогда и только тогда, когда в любой окрестности точки a содержится бесконечное число членов последовательности.
Доказательство ⇓

Верхний и нижний частичные пределы

Рассмотрим множество частичных пределов последовательности. Эта теорема утверждает, что верхняя и нижняя грани этого множества являются ее элементами. То есть множество частичных пределов последовательности замкнуто, оно содержит свою границу. Для произвольного множества это может не выполняться. Например, для открытого интервала не существует наибольшего и наименьшего элемента, поскольку и верхняя грань b и нижняя a не принадлежит этому множеству.

Если последовательность не ограничена сверху, то ее верхний частичный предел равен плюс бесконечности:
.
Соответственно, если последовательность не ограничена снизу, то
.

Если последовательность ограничена, то ее верхний и нижний частичные пределы конечны.

8. Теорема о неравенстве между верхним и нижним частичными пределами
Верхний и нижний частичные пределы последовательности удовлетворяют неравенству:
.
Частичные пределы равны друг другу тогда и только тогда, когда существует предел последовательности:
.
Доказательство ⇓

9. Связь верхних и нижних пределов между последовательностями n> и <–x_n>.
Имеет место очевидное равенство:
.

10. Свойства верхних и нижних пределов суммы последовательностей
Верхний и нижний частичные пределы от суммы последовательностей удовлетворяют следующим неравенствам:
;
,
где последовательности и ограничены.
Доказательство ⇓

11. Свойство верхних пределов произведения последовательностей
Пусть последовательность сходится к конечному положительному числу:
.
И пусть – любая последовательность. Тогда
.
Отсюда
.
Доказательство ⇓

Применяя равенство
,
можно получить другие подобные соотношения.

Доказательство свойств и теорем

Далее перечислены определения и свойства, которые мы будем использовать при доказательстве свойств подпоследовательностей.

1. Свойство подпоследовательностей сходящейся последовательности

2. Свойство последовательности, все подпоследовательности которой сходятся к одному числу

5. Свойство частичного предела последовательности

Все свойства ⇑ Точка является частичным пределом последовательности тогда и только тогда, когда в любой окрестности точки a содержится бесконечное число членов последовательности.

Возьмем произвольную окрестность точки a : ⇑. В качестве первого члена подпоследовательности возьмем любой член последовательности, принадлежащий этой окрестности.

6. Теорема о существовании верхнего и нижнего частичных пределов

В этом случае точка является верхним частичным пределом последовательности.

Пусть последовательность ограничена сверху и при этом любой отрезок содержит только конечное число членов последовательности.

Поскольку мы выбирали самые правые отрезки с бесконечным числом членов, то точка c является верхним частичным пределом последовательности.

7. Свойство верхнего и нижнего частичных пределов

8. Теорема о неравенстве между верхним и нижним частичными пределами

Все свойства ⇑ Верхний и нижний частичные пределы последовательности удовлетворяют неравенству:
.
Частичные пределы равны друг другу тогда и только тогда, когда существует предел последовательности:
.

10. Свойства верхних и нижних пределов суммы последовательностей

Все свойства ⇑ Верхний и нижний частичные пределы от суммы последовательностей удовлетворяют следующим неравенствам:
;
,
где последовательности и ограничены.

Докажем второе неравенство:
.
Умножим первое неравенство на – 1 :
.
Применим свойство 8 ⇑:
.

11. Свойство верхних пределов произведения последовательностей

Все свойства ⇑ Пусть последовательность сходится к конечному положительному числу:
.
И пусть – любая последовательность. Тогда
.
Отсюда
.

Из (10.1) и (10.2) следует, что
.
Свойство доказано.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Верхний и нижний пределы последовательности

Верхний и нижний пределы последовательности

Верхний и нижний пределы последовательности. В разделе 4.6 показано, что числовая последовательность всегда имеет по крайней мере 1 частичный предел, либо конечный, либо бесконечный. Максимум и минимум из них (учитывая ниже, что они всегда присутствуют) это играОн играет особую роль в теории последовательностей. Здесь понятия «максимум» и «минимум» понимаются в смысле расширенного набора действительных чисел K (см.§ 3.1).То есть наибольший (наименьший) элемент множества X ^ K в частности равен+ then (соответственно), что делается при+€€ € (—это€X).в данном случае это означает, что бесконечность соответствующего знака является частичным ограничением рассматриваемой последовательности. Не все наборы расширенных числовых строк имеют максимальный (минимальный) элемент.

Множество его конечных пределов, обозначенных через а, не является пустым или пустым. Людмила Фирмаль

Для любого числа n, например n’N и xn’A-e, существует число n ’(зависящее от e и n). Условие 1 означает, что для любого фиксированного e в последовательности существует только конечное число членов xn, таких как xn a + e (эти числа не больше ne). Условие 2 означает, что для любого фиксированного e в последовательности существует бесконечно много таких членов xn. Доказательство необходимости. Давайте попробуем это исправить. Если в полупериоде существует бесконечно много членов последовательности [a + e,+ then), то существует подпоследовательность, элементы которой принадлежат этому полупериоду и имеют конечные или бесконечные пределы. очевидно, что b A + e A противоречит тому факту, что a является максимальным частичным ограничением последовательности. Условие 1 доказано.

Здесь мы указываем, что число a является самым большим частичным пределом. Людмила Фирмаль

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Что такое верхний предел

Докажем, что верхний предел последовательности является её частичным пределом.

Напомним необходимые определения.

Напомним, что верна

Теорема (Больцано-Вейерштрасса).
Любая ограниченная последовательность имеет сходящуюся подпоследовательность.

Опр. Число M называется точной верхней гранью множества L, если

Опр. Верхним пределом последовательности называют супремум
множества частичных пределов, т.е.

где м-во частичных пределов.

Задача. Доказать, что для любой последовательности

также является её частичным пределом. Т.е. что

Решение.

Напомним, что для любой последовательности не пусто и
что для любого непустого множества супремум существует.
Пусть (может оказаться, что ).

Тогда по определению супремума

По определению предела

Тогда существует подпоследовательность такая, что

Для него тоже существует подпоследовательность

(может быть другая), такая, что

Т.к. это условие выполнено для сколь угодно больших номеров

При этом по построению верно, что

т.е. определяют первые два члена подпоследовательности.

Источник

Верхний и нижний пределы последовательности.

Всякая ограниченная последовательность имеет хотя бы одну предельную точку.

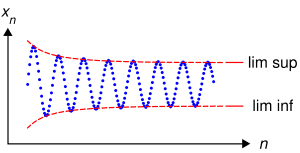
Определение. Наибольшая (наименьшая) из предельных точек ограниченной последовательности <x_n> наз. ёе верхним (нижним) пределом и обозначается: .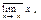

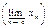
Если последовательность <x_n> сходится, то она имеет ровно одну предельную точку (ее предел), и в этом случае = = .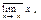

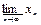
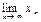
Если ограниченная последовательность имеет конечное число предельных точек, то среди них, очевидно, есть наибольшая и наименьшая, то есть в этом случае последовательность имеет верхний и нижний пределы. Если же число предельных точек бесконечно, то существование верхнего и нижнего пределов не является очевидным.

Теорема 6.3. Любая ограниченная последовательность имеет верхний и нижний пределы.

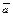
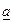
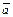
Достаточно доказать, что Î <a>, Î <a>. Проведем доказательство для .

Рассмотрим произвольную e-окрестность точки и, кроме того, рассмотрим -окрестность точки .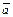

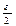
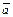
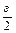
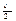
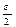
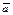
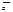
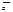
По определению точной верхней грани, существует точка a Î <a>: a Î < -окрестности точки a>, а по определению 2 предельной точки в -окрестности точки a содержится бесконечно много членов последовательности <x_n>. Но < -окрестность точки a> Ì >, тем самым, в e-окрестности точки содержится бесконечно много членов последовательности <x_n>, а это и означает, что — предельная точка последовательности <x_n>, то есть Î <a>.

БИЛЕТ 12

Числовая последовательность удовлетворяет условию Коши называется фундаментальной. Можно доказать, что и справедлива и обратное утверждение. Таким образом мы имеем критерий (необходимое и достаточное условие) сходимости последовательности.

В заключении рассмотрим вопрос критерия сходимости числовой последовательности.

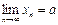
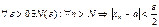
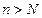
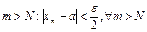
Пусть т.е.: на ряду с натуральным числом можно подставить в последнее неравенство другое натуральное число ,тогда

Мы получили следующее утверждение:

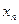
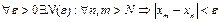
Если последовательность сходится, выполняется условие Коши:

(5)

Числовая последовательность удовлетворяет условию Коши называется фундаментальной. Можно доказать, что и справедлива и обратное утверждение. Таким образом мы имеем критерий (необходимое и достаточное условие) сходимости последовательности.

Критерий Коши.

Для того, чтобы последовательность имела предел необходимо и достаточно, что бы она была фундаментальной.

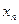
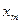
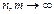
Второй смысл критерия Коши. Члены последовательности и где n и m – любые неограниченно сближающиеся при .

БИЛЕТ 13

Односторонние пределы.

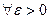
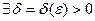
Определение 13.11. Число А называется пределом функции у = f(x) при х, стремящемся к х₀ слева (справа), если такое, что |f(x)-A|

Обозначения:

Теорема 13.1(второе определение предела). Функция y=f(x) имеет при х, стремящемся к х₀, предел, равный А, в том и только в том случае, если оба ее односторонних предела в этой точке существуют и равны А.

Источник