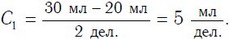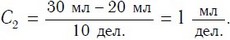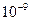Что такое верхний предел измерения
§ 7. Измерительные приборы. Цена деления. Точность измерений
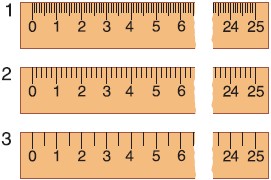
На рисунке 39 изображены три линейки с одинаковыми верхними пределами (25 см). Но эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 1, менее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала цену деления шкалы прибора.
Цена деления — это значение наименьшего деления шкалы прибора.
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
C1 = 1 см : 10 дел = 0,1 см/дел
C2 = 1 см : 5 дел = 0,2 см/дел
C3 = 1 см : 2 дел = 0,5 см/дел
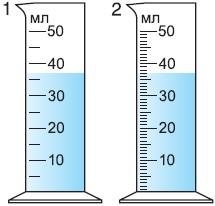
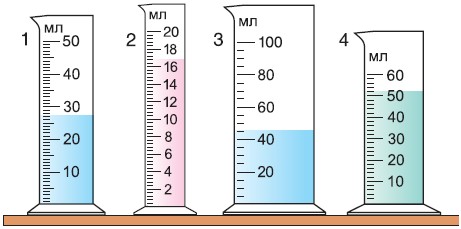
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 40). Цена деления шкалы мензурки 1:
Цена деления шкалы мензурки 2:
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Исходя из показаний шкалы объем воды в мензурке 1:
V = 35 мл.
Из показаний шкалы мензурки 2:
V = 37 мл.
Понятно, что точнее измерен объем воды мензуркой 2, цена де- ления которой меньше (1 мл/дел
верхний предел измерений
5.2.22 верхний предел измерений (upperlimitof measurement): Максимальное значение характеристики качества воздуха, которое может быть получено при допускаемых значениях характеристик (метода).
Смотри также родственные термины:
57 верхний предел измерений без перестройки диапазона (гравиметра)
Максимальное значение разности силы тяжести, которое может быть измерено данным гравиметром с нормированной погрешностью без перестройки диапазона измерений гравиметра.
58 верхний предел измерений с перестройкой диапазона (гравиметра)
Максимальное значение разности силы тяжести, которое может быть измерено данным гравиметром с нормированной погрешностью с применением перестройки диапазона измерений гравиметра.
10. Верхний предел измерений тензорезисторного датчика силы
Верхний предел измерений датчика
11. Предельная нагрузка тензорезисторного датчика силы
Предельная нагрузка датчика
Наибольшее значение внешней силы, не нарушающей работоспособность тензорезисторного датчика силы
Полезное
Смотреть что такое «верхний предел измерений» в других словарях:
верхний предел измерений — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN full scale value … Справочник технического переводчика
верхний предел измерений — galutinė matavimo srities riba statusas T sritis Standartizacija ir metrologija apibrėžtis Didžiausias leidžiamasis matavimo priemonės rodmuo. atitikmenys: angl. full scale value vok. maximal zulässiger Ablesewert, m rus. верхний предел измерений … Penkiakalbis aiškinamasis metrologijos terminų žodynas
верхний предел измерений тензорезисторного датчика силы — верхний предел измерений датчика Значение измеряемой силы, соответствующее верхней границе измерений тензорезисторного датчика силы, для которого нормированы допускаемые погрешности. [ГОСТ 16217 83] Тематики датчики и преобразователи физических… … Справочник технического переводчика
верхний предел измерений без перестройки диапазона (гравиметра) — Максимальное значение разности силы тяжести, которое может быть измерено данным гравиметром с нормированной погрешностью без перестройки диапазона измерений гравиметра. [ГОСТ Р 52334 2005 ] Тематики гравиразведка и магниторазведка EN counter… … Справочник технического переводчика
верхний предел измерений с перестройкой диапазона (гравиметра) — Максимальное значение разности силы тяжести, которое может быть измерено данным гравиметром с нормированной погрешностью с применением перестройки диапазона измерений гравиметра. [ГОСТ Р 52334 2005 ] Тематики гравиразведка и магниторазведка EN… … Справочник технического переводчика
верхний предел измерений (прибора) — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN full scale value … Справочник технического переводчика
Верхний предел измерений тензорезисторного датчика силы — 10. Верхний предел измерений тензорезисторного датчика силы Верхний предел измерений датчика 11. Предельная нагрузка тензорезисторного датчика силы Предельная нагрузка датчика Наибольшее значение внешней силы, не нарушающей работоспособность… … Словарь-справочник терминов нормативно-технической документации
верхний предел измерений без перестройки диапазона (гравиметра) — 57 верхний предел измерений без перестройки диапазона (гравиметра) Максимальное значение разности силы тяжести, которое может быть измерено данным гравиметром с нормированной погрешностью без перестройки диапазона измерений гравиметра. Источник:… … Словарь-справочник терминов нормативно-технической документации
верхний предел измерений с перестройкой диапазона (гравиметра) — 58 верхний предел измерений с перестройкой диапазона (гравиметра) Максимальное значение разности силы тяжести, которое может быть измерено данным гравиметром с нормированной погрешностью с применением перестройки диапазона измерений гравиметра.… … Словарь-справочник терминов нормативно-технической документации
ГОСТ Р ИСО 6879-2005: Качество воздуха. Характеристики и соответствующие им понятия, относящиеся к методам измерений качества воздуха — Терминология ГОСТ Р ИСО 6879 2005: Качество воздуха. Характеристики и соответствующие им понятия, относящиеся к методам измерений качества воздуха оригинал документа: 5.2.2 аналитическая функция (analytical function): Функция, обратная… … Словарь-справочник терминов нормативно-технической документации
Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.
Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать
Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: 

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
На точность измерения влияет много факторов, в частности:
Все это необходимо учитывать при проведении измерений.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.
Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.
Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:
Цена деления шкалы мензурки 2:
А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
Пример решения задачи
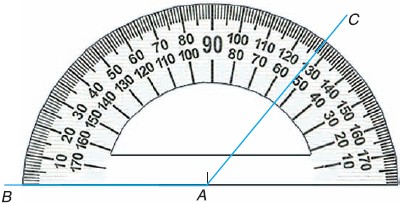
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.
Решение:
1) Цена деления нижней шкалы:
Цена деления средней шкалы:
Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10° 

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Лекция 3. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
Метрологические характеристики прибора – это те, которые непосредственно связаны с его основным назначением – производством измерений. В эти характеристики входят пределы измерения, основная и дополнительные погрешности и класс точности.
Верхний и нижний пределы измерения ограничивают область (диапазон) использования прибора и поэтому представляют собой наиболее важную его характеристику. Чаще всего нижним пределом измерения прибора является нуль, что означает что, измеряемая величина, как таковая, отсутствует. Однако, это не всегда так. Иногда нуль располагается между верхним и нижним пределами и делит значения измеряемой величины на положительные и отрицательные. Пример – шкала термометра. Диапазон измерения
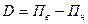
где 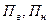
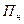
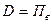
если же
При таком подходе (при условном постоянстве абсолютной погрешности) относительная погрешность измерения прибором (формула 1.7) приводится к виду
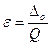
Таблица 3.2. Значения 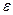
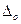
Числовые отметки, 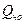 , МПа , МПа | ||||||
Относительные ошибки, 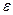 | — | 0.075 | 0.038 | 0.025 | 0.019 | 0.015 |
Из таблицы 3.2 (продолжение примера, данного в таблице 3.1) видно, что относительные погрешности максимальны на наименьшей числовой отметке и минимальны (равны классу точности) на наибольшей отметке. Это следует из формулы (3.7). Пример подтверждает правило, согласно которому разовые измерения желательно проводить в верхней трети шкалы. Это обеспечит наибольшую точность измерений.
Соответственно, ожидаемое значение измеряемой величины должно быть
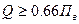
Наоборот, при выборе прибора для разовых измерений величины 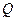
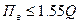
Требуемый класс точности определяют по заданной максимально допустимой относительной погрешности 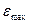
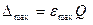
При выборе метрологических характеристик прибора непрерывного действиянеобходимо знать ожидаемый диапазон измеряемой величины от 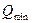
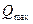
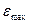
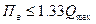
Максимальная абсолютная погрешность
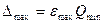
и приведенная погрешность 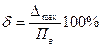
По приведенной погрешности из параметрического ряда выбирают соответствующий класс точности. Необходимо подчеркнуть, что при выборе приборав соответствии с заданной целью измерения, из ряда следует брать не ближайшее большее значение (как приоценкеточности прибора – см выше, формулы (3.4) – (3.6)), а наоборот, – ближайшее меньшее значение. В противном случае не выполняется требование непревышения заданного максимума относительной погрешности 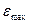
Для примера в таблице 3.3 заданы требования к исходным параметрам расхода
Таблица 3.3. Выбор метрологических характеристик бурового расходомера
| Параметр, символ, единица | Значение | Формула |
| Исходные данные | ||
Минимальный расход, 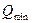 , л/с , л/с | ||
Максимальный расход, 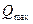 , л/с , л/с | ||
Максимальная относительная погрешность, 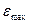 | 0.1 | |
| Результаты расчетов | ||
Верхний предел измерения расходомера, 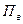 , л/с , л/с | (3.11) | |
Максимальная абсолютная погрешность, 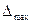 , л/с , л/с | 0.5 | (3.12) |
Приведенная погрешность, 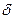 , % , % | 1.25 | (3.13) |
Класс точности, 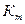 ,% ,% | (из параметрического ряда) | |
Основная погрешность, 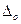 , л/с , л/с | 0.4 | (3.5) |
промывочной жидкости и по ним найдены метрологические характеристики расходомера.
Чем выше класс точности прибора, тем он дороже, сложнее в эксплуатации и обслуживании, чаще требует поверок и ремонтов. Поэтому надо стремиться использовать приборы возможно более низких классов точности, но при этом достигать необходимой точности измерений. Это достигается применением многопредельных приборов.
По формуле (3.12) принимающей вид 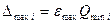
вычисляют 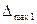
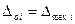
Преобразуя формулу (3.5), получают значение верхнего предела измерения
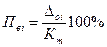
Принимают верхний предел первого диапазона за минимум измеряемой величины на втором диапазоне 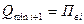
Далее определяют 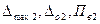
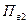
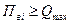
то выбирают двухдиапазонный прибор, иначе рассчитывают третий диапазон и т. д.
Пример. Для условий предыдущего примера ( 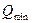
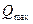
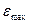
Таблица 3.4. Расчет многопредельного расходомера с классом точности 4%
| Параметр, символ, единица | Значение | Формула |
| Первый диапазон измерения | ||
Минимальный расход, 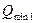 , л/с , л/с | (3.14) | |
Максимальная абсолютная погрешность, 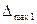 , л/с , л/с | 0.5 | (3.15) |
Основная погрешность, 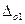 , л/с , л/с | 0.5 | (3.16) |
Верхний предел измерения расходомера, 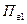 , л/с , л/с | (3.17) | |
| Второй диапазон измерения | ||
Минимальный расход, 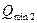 , л/с , л/с | (3.18) | |
Максимальная абсолютная погрешность, 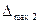 , л/с , л/с | 1.2 | (3.15) |
Основная погрешность, 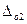 , л/с , л/с | 1.2 | (3.16) |
Верхний предел измерения расходомера, 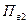 , л/с , л/с | 30* | (3.17) |
* Удовлетворяет условию (3.19), поэтому прибор остается двухдиапазонным
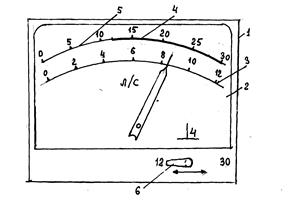
Рис.3.1 Расходомер с двухпредельной шкалой
1 – корпус показывающего прибора; 2 – циферблат; 3 – шкала нижнего диапазона; 4 – рабочая часть шкалы верхнего диапазона; 5 – нерабочая (относящаяся к нижнему диапазону) часть шкалы верхнего диапазона; 6 – переключатель диапазонов
На работу измерительного прибора и, в частности, на его точность, сильное влияние оказывают факторы внешней среды. К ним относятся климатические факторы, механические факторы, а для электрических приборов также и параметры питающей сети. Температура окружающего воздуха, его влажность, атмосферное давление относятся к климатическим факторам; наличие вибраций, сотрясений; ударов, пыли и брызгов – к механическим факторам; питающая сеть характеризуется напряжением и частотой.
Существуют так называемые нормальные условия измерения. Нормальными условиями измерения называют такие, при которых все влияющие факторы внешней среды находятся у значений (или в пределах некоторых интервалов значений), которые согласно паспорту данного прибора считаются нормальными. Так, нормальной температурой для большинства приборов, включая приборы контроля режима бурения, считается 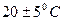
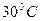
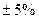
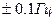
Выше указывалось, что при нормальных условиях измерения погрешность прибора не должна превышать значение его основной погрешности 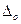
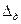
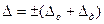
Дополнительная погрешность в этой формуле зависит от всех влияющих факторов, рассматриваемых вместе. Дополнительная погрешность по какому-то одному влияющему факторуА 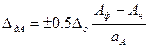
В этой формуле 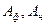
Таблица 3.5. Значения стандартного отклонения
| Наименование влияющего фактора | Стандартное отклонение 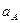 |
Температура окружающего воздуха, 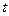 , градусов , градусов | |
Напряжение питающей сети, 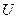 , % от номинального , % от номинального | |
Частота питающей сети, 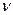 , Гц , Гц |
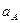
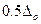
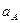
После установления дополнительных погрешностей, по всем, отклонившимся от нормальных условий факторам 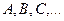
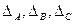
Таблица 3.6. Общая допустимая погрешность электрического манометра
| Параметр, символ, единица | Значение | Формула |
| Исходные данные | ||
Основная погрешность, 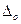 , МПа , МПа | 0.1 | |
Нормальная температура, 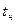 , град , град | ||
Фактическая температура, 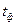 , град , град | ||
Стандартное отклонение температуры от нормальной, 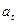 , град , град | ||
Нормальная частота сети, 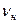 , Гц , Гц | ||
Фактическая частота сети, 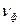 , Гц , Гц | ||
Стандартное отклонение частоты от нормальной, 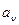 , Гц , Гц | ||
| Результаты расчетов | ||
Дополнительная погрешность по температуре, 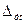 , МПа , МПа | 0.1 | (3.21) |
Дополнительная погрешность по частоте, 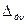 , МПа , МПа | 0.15 | (3.21) |
Суммарная дополнительная погрешность, 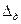 , МПа , МПа | 0.18 | (3.22) |
Общая допустимая погрешность, 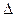 , МПа , МПа | 0.28 | (3.20) |
дополнительная погрешность определяется как
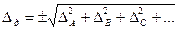
Пример нахождения общей допустимой погрешности манометра при отклонениях влияющих факторов внешней среды от нормальных условий приведен в таблице 3.6
Все измерительные приборы должны периодически – с периодичностью, указанной в их паспорте – проходить поверку. Часто такой период равняется одному году. Цель поверки – убедиться, что за очередной период эксплуатации основная и дополнительные погрешности прибора не вышли за допустимые пределы.
По отношению к поверке все приборы делятся на три группы: эталоны, образцовые приборы и рабочие приборы. Эталономназывается измерительное средство, обладающее наивысшей точностью, достижимой на данном этапе развития науки и техники. Так, если 50 лет назад эталоном метра было расстояние между насечками на платиноиридиевом стержне, то в наше время эталон метра считается равным 1650763.73 длин волны излучения, соответствующего оранжевой линии в спектре криптона-86. Абсолютная погрешность числа равна половине его последнего знака, т. е, в случае указанного числа длин волн – это 0.005 от длины одной волны (число заканчивается сотыми) Отсюда относительная погрешность (формула(1.7)) эталона метра 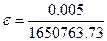
Существуют первичные, вторичные и третичные эталоны. Каждая основная единица системы СИ имеет свой эталон, хранящийся в Бюро мер и весов в Париже. Все государства, использующие систему СИ имеют одну копию этого эталона в качестве своего первичного-государственного эталона данной единицы. По первичному эталону, как по образцу, выполняется несколько вторичных эталонов, по ним – гораздо большее число третичных эталонов. Первичные эталоны постоянно находится на хранении в специальной организации (в России – это Институт метрологии им. Д.И. Менделеева в Санкт Петербурге). Все влияющие факторы внешней среды в помещении хранения строго стабилизированы. Третичные эталоны хранятся в крупных городах. По первичным эталонам периодически проходят поверку соответствующие вторичные эталоны, по вторичным – третичные эталоны, по третичным так называемые образцовые приборы.
Образцовые приборы служат для поверки, и градуировки рабочих приборов, используемых на различных производствах для контроля применяемой технологии. Поверять одни рабочие приборы с помощью других (пусть более точных) рабочих приборов запрещено. Используемый для поверки образцовый прибор должен иметь тот же диапазон измерения, что и поверяемый прибор. Основная погрешность образцового прибора должна быть не более 0.1 от основной погрешности поверяемого прибора (в исключительных случаях это соотношение может быть повышено до 0.33)
Процедура поверки заключается в том, что рабочий и образцовый приборы помещаются в одну и ту же измерительную магистраль (см., например рис. 2.1) поверочной установки. Поверка производится на всех числовых отметках (как в таблице 3.1), причем по формуле (1.6) определяется 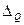
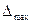
Если проверяется основная погрешность прибора, то ее вычисленное по формуле (3.5) значение сравнивают с 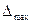
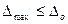
Если проводится поверка дополнительной погрешности, то прибор помещают в условия, когда рассматриваемый фактор 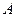
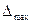
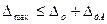
где 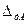
Если условия (3.23) и (3.24) соблюдены, то прибор выдержал поверку, и в его паспорте ставят соответствующую отметку с разрешением использования в течение следующего межповерочного срока. В противном случае прибор считается неисправным и его использование запрещается. Тогда он либо сдается на юстирование ( ремонт с целью повышения точности ), либо списывается.
Рекомендуемая литература: 1. с. 61-72.
1. Что такое пределы измерения прибора?
2. Что такое класс точности и как его находят?
3. Как выбрать прибор, если известны требования к результатам измерений?
4. Что такое основная и дополнительная погрешности измерительного прибора?
5. Как классифицируют измерительные средства, участвующие в поверке?