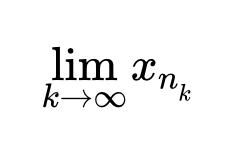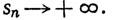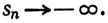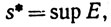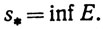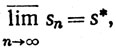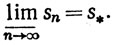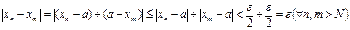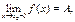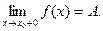Что такое верхний и нижний пределы

Подпоследовательности и частичные пределы последовательностей

Определение подпоследовательности

Свойства подпоследовательностей

Свойство 3 является следствием свойств 1 и 2.

Частичный предел последовательности

Произвольная последовательность может иметь конечное или бесконечное число частичных пределов ⇑.

5. Свойство частичного предела последовательности
Точка является частичным пределом последовательности тогда и только тогда, когда в любой окрестности точки a содержится бесконечное число членов последовательности.
Доказательство ⇓

Верхний и нижний частичные пределы

Рассмотрим множество частичных пределов последовательности. Эта теорема утверждает, что верхняя и нижняя грани этого множества являются ее элементами. То есть множество частичных пределов последовательности замкнуто, оно содержит свою границу. Для произвольного множества это может не выполняться. Например, для открытого интервала не существует наибольшего и наименьшего элемента, поскольку и верхняя грань b и нижняя a не принадлежит этому множеству.

Если последовательность не ограничена сверху, то ее верхний частичный предел равен плюс бесконечности:
.
Соответственно, если последовательность не ограничена снизу, то
.

Если последовательность ограничена, то ее верхний и нижний частичные пределы конечны.

8. Теорема о неравенстве между верхним и нижним частичными пределами
Верхний и нижний частичные пределы последовательности удовлетворяют неравенству:
.
Частичные пределы равны друг другу тогда и только тогда, когда существует предел последовательности:
.
Доказательство ⇓

9. Связь верхних и нижних пределов между последовательностями n> и <–x_n>.
Имеет место очевидное равенство:
.

10. Свойства верхних и нижних пределов суммы последовательностей
Верхний и нижний частичные пределы от суммы последовательностей удовлетворяют следующим неравенствам:
;
,
где последовательности и ограничены.
Доказательство ⇓

11. Свойство верхних пределов произведения последовательностей
Пусть последовательность сходится к конечному положительному числу:
.
И пусть – любая последовательность. Тогда
.
Отсюда
.
Доказательство ⇓

Применяя равенство
,
можно получить другие подобные соотношения.

Доказательство свойств и теорем

Далее перечислены определения и свойства, которые мы будем использовать при доказательстве свойств подпоследовательностей.

1. Свойство подпоследовательностей сходящейся последовательности

2. Свойство последовательности, все подпоследовательности которой сходятся к одному числу

5. Свойство частичного предела последовательности

Все свойства ⇑ Точка является частичным пределом последовательности тогда и только тогда, когда в любой окрестности точки a содержится бесконечное число членов последовательности.

Возьмем произвольную окрестность точки a : ⇑. В качестве первого члена подпоследовательности возьмем любой член последовательности, принадлежащий этой окрестности.

6. Теорема о существовании верхнего и нижнего частичных пределов

В этом случае точка является верхним частичным пределом последовательности.

Пусть последовательность ограничена сверху и при этом любой отрезок содержит только конечное число членов последовательности.

Поскольку мы выбирали самые правые отрезки с бесконечным числом членов, то точка c является верхним частичным пределом последовательности.

7. Свойство верхнего и нижнего частичных пределов

8. Теорема о неравенстве между верхним и нижним частичными пределами

Все свойства ⇑ Верхний и нижний частичные пределы последовательности удовлетворяют неравенству:
.
Частичные пределы равны друг другу тогда и только тогда, когда существует предел последовательности:
.

10. Свойства верхних и нижних пределов суммы последовательностей

Все свойства ⇑ Верхний и нижний частичные пределы от суммы последовательностей удовлетворяют следующим неравенствам:
;
,
где последовательности и ограничены.

Докажем второе неравенство:
.
Умножим первое неравенство на – 1 :
.
Применим свойство 8 ⇑:
.

11. Свойство верхних пределов произведения последовательностей

Все свойства ⇑ Пусть последовательность сходится к конечному положительному числу:
.
И пусть – любая последовательность. Тогда
.
Отсюда
.

Из (10.1) и (10.2) следует, что
.
Свойство доказано.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Частичный предел последовательности

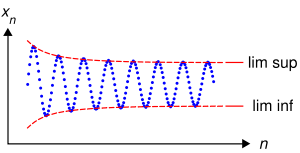
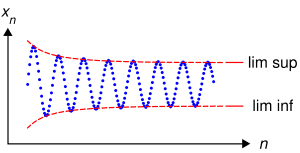
Частичный предел некоторой последовательности — это предел одной из её подпоследовательностей, если только он существует. Для сходящихся числовых последовательностей частичный предел совпадает с обычным пределом в силу единственности последнего, однако в самом общем случае у произвольной последовательности может быть от нуля до бесконечного числа различных частичных пределов. При этом, если обычный предел характеризует точку, к которой элементы последовательности приближаются с ростом номера, то частичные пределы характеризуют точки, вблизи которых лежит бесконечно много элементов последовательности.

Два важных частных случая частичного предела — верхний и нижний пределы.

Содержание

Определение

Частичным пределом последовательности называется предел какой-либо её подпоследовательности, если существует хотя бы одна подпоследовательность, имеющая предел. В противном случае, говорят, что у последовательности нет частичных пределов. В некоторой литературе в случаях, если из последовательности удаётся выделить бесконечно большую подпоследовательность, все элементы которой одновременно положительны или отрицательны, её частичным пределом называют соответственно или .

Нижний предел последовательности — это точная нижняя грань множества частичных пределов последовательности.

Верхний предел последовательности — это точная верхняя грань множества частичных пределов последовательности.

Иногда нижним пределом последовательности называют наименьшую из её предельных точек, а верхним — наибольшую. [1] Очевидно, что эти определения эквивалентны.

Обозначения

Нижний предел последовательности :

Верхний предел последовательности :

Примеры

Свойства

Примечания

Полезное

Смотреть что такое «Частичный предел последовательности» в других словарях:

Частичный предел — Верхний предел (lim sup) и нижний предел (lim inf) последовательности. Частичным пределом последовательности называется предел какой либо её подпоследовательности, если существует хотя бы одна подпоследовательность, имеющая предел. Очевидно, что… … Википедия

ЧАСТИЧНЫЙ ПРЕДЕЛ — данной последовательности предел нек рой ее подпоследовательности. У всяком числовой последовательности (а также у всякой последовательности точек конечномерного евклидова пространства) существует, по крайней мере, один Ч. п. (конечный или… … Математическая энциклопедия

Предел числовой последовательности — Предел числовой последовательности предел последовательности элементов числового пространства. Числовое пространство это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому, предел … Википедия

Предел — объект, представляющий собой воображаемую или реальную границу для другого объекта. В математическом анализе см. Предел (математика), а также: Предел последовательности Предел функции Предел категории Частичный предел Проективный предел Банаховы… … Википедия

ПРЕДЕЛ — одно из основных понятий математики, означающее, что какая то переменная, зависящая от другой переменной, при определенном изменении последней, неограниченно приближается к нек рому постоянному значению. Основным при определении П. является… … Математическая энциклопедия

Предел (математика) — У этого термина существуют и другие значения, см. Предел. Предел одно из основных понятий математического анализа. Различают предел последовательности и предел функции. Понятие предела на интуитивном уровне использовалось ещё во второй половине… … Википедия

Предел — одно из основных понятий математики. П. постоянная, к которой неограниченно приближается некоторая переменная величина, зависящая от другой переменной величины, при определённом изменении последней. Простейшим является понятие П. числовой … Большая советская энциклопедия

Числовая последовательность — Последовательность Числовая последовательность это последовательность элементов числового пространства. Числовые пос … Википедия

Асимптотическая плотность — В теории чисел асимптотическая плотность это одна из характеристик, помогающих оценить, насколько велико подмножество множества натуральных чисел … Википедия

Источник

Нижний предел

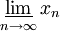
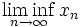
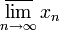
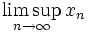
Нижним пределом последовательности (обозначается или ) называется наименьший элемент множества частичных пределов последовательности, а верхним пределом ( или ) — наибольший элемент.

Докажем это утверждение для верхнего предела. По теореме Больцано — Вейерштрасса множество частичных пределов ограниченной последовательности непусто. Пусть s — верхняя грань множества A частичных пределов. Тогда заметим, что 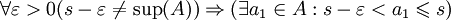, а это означает, что в любой окрестности точки a₁ находится бесконечно много членов последовательности. Поскольку утверждение верно для любого , мы можем сказать, что в любой окрестности точки s содержится бесконечно много членов последовательности (так как в любой окрестности мы можем найти точку a₁ ). Значит, s по определению является предельной точкой последовательности, а стало быть, и её частичным пределом, что и требовалось доказать. Аналогично доказывается случай нижнего предела.

Последовательность <x_n> сходится к a тогда и только тогда, когда 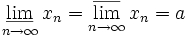, так как получается, что a — единственная предельная точка множества элементов последовательности.

Полезное

Смотреть что такое «Нижний предел» в других словарях:

нижний предел — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN inferior limitsmallest extreme … Справочник технического переводчика

нижний предел — apatinė riba statusas T sritis automatika atitikmenys: angl. inferior limit; lower limit vok. untere Grenzwert, m; Untergrenze, f rus. нижний предел, m pranc. limite inférieure, f … Automatikos terminų žodynas

нижний предел — apatinė riba statusas T sritis fizika atitikmenys: angl. inferior limit; lower limit vok. untere Grenze, f; unterer Grenzwert, m rus. нижний предел, m; нижняя граница, f pranc. limite inférieure, f … Fizikos terminų žodynas

нижний предел критической температуры фазового перехода или превращения — нижний предел критической точки фазового перехода или превращения — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом Синонимы нижний предел критической точки фазового перехода или превращения EN… … Справочник технического переводчика

Предел текучести физический (нижний предел текучести) s_т — Наименьшее напряжение, при котором образец деформируется без заметного увеличения растягивающего усилия Источник: ГОСТ 1497 84: Металлы. Методы испытаний на растяжение оригинал документа … Словарь-справочник терминов нормативно-технической документации

Нижний предел воспламенения — (НПВ) концентрация углеводородного газа в воздухе, ниже которой невозможно поддержание и распространение процесса горения (для газовых смесей, образующихся от выделения углеводородного газа нефтепродуктами в воздушную атмосферу судовых помещений … Официальная терминология

нижний предел взрываемости (метана) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN lower explosive limit … Справочник технического переводчика

нижний предел взрывоопасности — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN lower explosive limitLEL … Справочник технического переводчика

нижний предел воспламеняемости — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN lower flammable limit … Справочник технического переводчика

Источник

Что такое верхний и нижний пределы

Верхний и нижний пределы

Аналогичным образом, если для любого вещественного числа М существует целое N, такое, что при n≥N мы имеем s_n≤M, то мы пишем

Следует отметить, что мы теперь используем символ → (введенный в определении 3.1) для некоторых типов расходящихся последовательностей, так же как и для сходящихся последовательностей, но что определения сходимости и предела, данные в п. 3.1, никоим образом не меняются.

Вспомним теперь определения 1.34 и 1.40 и положим

Конечно, аналогичный результат верен для s_*.

Доказательство. Если s * = +∞, то множество Е не ограничено сверху; значит, последовательность n> не ограничена сверху и существует подпоследовательность n_k>, такая, что s_nk→+∞.

Тем самым (а) установлено во всех случаях.

Таким образом, s * удовлетворяет условиям (а) и (b).

Для доказательства единственности допустим, что существуют два числа р и q, удовлетворяющие условиям (а) и (b), и допустим, что р

Источник

Верхний и нижний пределы последовательности.

Всякая ограниченная последовательность имеет хотя бы одну предельную точку.

Определение. Наибольшая (наименьшая) из предельных точек ограниченной последовательности <x_n> наз. ёе верхним (нижним) пределом и обозначается: .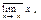

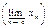
Если последовательность <x_n> сходится, то она имеет ровно одну предельную точку (ее предел), и в этом случае = = .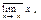

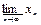
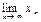
Если ограниченная последовательность имеет конечное число предельных точек, то среди них, очевидно, есть наибольшая и наименьшая, то есть в этом случае последовательность имеет верхний и нижний пределы. Если же число предельных точек бесконечно, то существование верхнего и нижнего пределов не является очевидным.

Теорема 6.3. Любая ограниченная последовательность имеет верхний и нижний пределы.

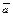
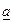
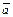
Достаточно доказать, что Î <a>, Î <a>. Проведем доказательство для .

Рассмотрим произвольную e-окрестность точки и, кроме того, рассмотрим -окрестность точки .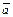

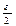
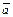
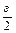
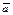
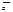
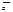
По определению точной верхней грани, существует точка a Î <a>: a Î < -окрестности точки a>, а по определению 2 предельной точки в -окрестности точки a содержится бесконечно много членов последовательности <x_n>. Но < -окрестность точки a> Ì >, тем самым, в e-окрестности точки содержится бесконечно много членов последовательности <x_n>, а это и означает, что — предельная точка последовательности <x_n>, то есть Î <a>.

БИЛЕТ 12

Числовая последовательность удовлетворяет условию Коши называется фундаментальной. Можно доказать, что и справедлива и обратное утверждение. Таким образом мы имеем критерий (необходимое и достаточное условие) сходимости последовательности.

В заключении рассмотрим вопрос критерия сходимости числовой последовательности.

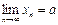
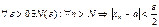
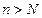
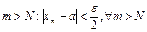
Пусть т.е.: на ряду с натуральным числом можно подставить в последнее неравенство другое натуральное число ,тогда

Мы получили следующее утверждение:

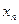
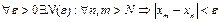
Если последовательность сходится, выполняется условие Коши:

(5)

Числовая последовательность удовлетворяет условию Коши называется фундаментальной. Можно доказать, что и справедлива и обратное утверждение. Таким образом мы имеем критерий (необходимое и достаточное условие) сходимости последовательности.

Критерий Коши.

Для того, чтобы последовательность имела предел необходимо и достаточно, что бы она была фундаментальной.

Второй смысл критерия Коши. Члены последовательности 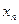и где n и m – любые неограниченно сближающиеся при .

БИЛЕТ 13

Односторонние пределы.

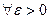
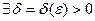
Определение 13.11. Число А называется пределом функции у = f(x) при х, стремящемся к х₀ слева (справа), если такое, что |f(x)-A|

Обозначения:

Теорема 13.1(второе определение предела). Функция y=f(x) имеет при х, стремящемся к х₀, предел, равный А, в том и только в том случае, если оба ее односторонних предела в этой точке существуют и равны А.

Источник