Что такое векторная диаграмма
Векторная диаграмма токов и напряжений
Процессы, протекающие в электроцепи переменного тока с активным сопротивлением и реактивной индуктивностью, можно наглядно выразить в графическом виде.
Статья даст описание, что такое векторные диаграммы, где и для чего они используются. Также будет описана временная диаграмма и ее назначение. В конце будет дан пример построения простой диаграммы для электроцепи с последовательным соединением элементов.
Определение
Векторная диаграмма токов и напряжений — это геометрическое изображение всех процессов, величин и амплитуд синусоидального тока. Все имеющиеся величины располагаются на плоскости в виде векторов.
Построение векторной диаграммы использует физика и электротехника. Благодаря созданию такой диаграммы можно значительно упростить выполняемые расчеты, а так же в наглядном и доступном виде отобразить происходящие процессы.
Метод векторных диаграмм позволяет также увидеть в цепи переменного тока возникающие короткие и межфазовые замыкания, а также вычислить возможные потери мощности.
Обычно такая диаграмма строится вместе с временной. Временная диаграмма — это графическое изображение входа и выхода в электрической цепи. Временные диаграммы помогают определить временной промежуток между началом, протеканием и окончанием сигнала. Например, при нажатии на кнопку возникает сигнал, который поступает к приемнику и запускает процесс его работы.
Временные диаграммы также применимы к синусоидальной электрической цепи, так как этот ток имеет начальную точку отсчета (включение питания) и время движения от источника тока к потребителю. Такие диаграммы представляют собой график, на котором изображается начальная точка отсчета, вектор времени и углы смещения фаз.
Разновидности
Разобравшись, что такое и для чего применяется векторная диаграмма, нужно узнать какие разновидности построения существуют. Они отличаются по характеру построения и типу. По характеру бывают:
Векторную диаграмму токов можно построить 2 разными способами:
Оба построения могут использоваться для расчета характеристик переменного тока в цепи с сопротивлением и индуктивностью.
Построение
Построение простых векторных диаграмм будет рассмотрено в данном разделе. Для примера можно взять простую цепь с несколькими элементами и их значениями. Такая схема подразумевает последовательное соединение элементов между собой. Цепь состоит из катушки индуктивности, конденсатора и активного сопротивления. Параметры каждого элемента цепи приведены ниже.
Далее можно сделать простую диаграмму, которая поможет определить напряжение для всей схемы.
Поэтому если есть схема с последовательным соединением элементов, то всегда можно довольно просто построить векторную диаграмму и рассчитать общее напряжение для такой схемы.
Способ 2
Построение векторных диаграмм с учетом всех известных значений для цепи переменного тока с последовательным соединением конденсатора, резистора и катушки индуктивности. При таком построении нам так же известно напряжение самой цепи. Цепь состоит из:
Данная диаграмма может использоваться для контроля и расчета влияния всех известных параметров цепи и элементов, а также их взаимосвязи между собой.
Основное преимущество векторной диаграммы заключается в следующем — простое и быстрое сложение, вычитание двух параметров во время расчета электрических цепей.
Понятие о векторах и векторных диаграммах также подразумевает расчет цепи питания трехфазной сети, подключенной по методу звезды. Она строится с учетом сразу 3 отложенных векторов от 0 оси ординат. Такое построение определяет вектор от источника тока к приемнику. Строится вектор со следующими значениями:
Далее нужно сделать:
Таким же образом на плоскость накладываются еще две прямые линии. Общая диаграмма покажет симметричность фаз или их сдвиг при появлении короткого замыкания. Такая диаграмма может стать примером для расчета напряжения, тока или нагрузки на каждую фазу с моделированием различных параметров.
Заключение
Векторные диаграммы сложны в понимании при расчете сложных цепей, с большим количеством сопротивлений и индуктивностью. Также, при расчете стоит учитывать тип соединения всех элементов, симметрию цепи и основные ее значения.
Видео по теме
Что такое векторные диаграммы и для чего они нужны
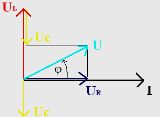
При расчете цепей переменного тока часто приходится суммировать (или вычитать) несколько однородных синусоидально изменяющихся величин одной и той же частоты, но имеющих разные амплитуды и начальные фазы. Такую задачу можно решать аналитическим путем тригонометрических преобразований или геометрически. Геометрический метод более прост и нагляден, чем аналитический.
Векторные диаграммы являются совокупностью векторов, изображающих действующие синусоидальные ЭДС и токи или их амплитудные значения.
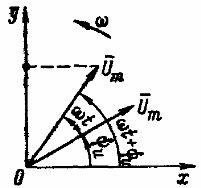
Гармонически изменяющееся напряжение определяется выражением u = Um sin ( ωt + ψ и ).
Рис. 1. Изображение синусоидального напряжения вращающегося вектора
При расчете цепи переменного тока часто приходится складывать ЭДС, токи или напряжения одной и той же частоты.
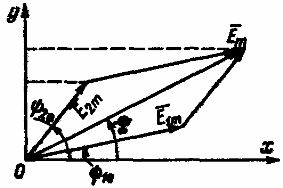
Такое сложение можно осуществить аналитически и графически. Последний способ более нагляден и прост. Две складываемые ЭДС е1 и е2 в определенном масштабе представлены векторами E1 m E 2m (рис. 2). При вращении этих векторов с одной и той же частотой вращения, равной угловой частоте, взаимное расположение вращающихся векторов остается неизменным.
Рис. 2. Графическое сложение двух синусоидальных ЭДС одинаковой частоты
Сумма проекций вращающихся векторов E1 m и E 2m на ось ординат равна проекции на ту же ось вектора E m, являющегося их геометрической суммой. Следовательно, при сложения двух синусоидальных ЭДС одной и той же частоты получается синусоидальная ЭДС той же частоты, амплитуда которой изображается вектором E m, равным геометрической сумме векторов E1 m и E 2m: E m = E1 m + E 2m.
Векторы переменных ЭДС и токов являются графическими изображениями ЭДС и токов в отличие от векторов физических величин, имеющих определенное физическое значение: вектора силы, напряженности поля и других.
Указанный способ можно применить для сложения и вычитания любого числа ЭДС и токов одной частоты. Вычитание двух синусоидальных величин можно представить в виде сложения: e1— e2 = e1+ (- e2), т. е. уменьшаемая величина складывается с вычитаемой, взятой с обратным знаком. Обычно векторные диаграммы строятся не для амплитудных значений переменных ЭДС и токов, а для действующих величин, пропорциональных амплитудным значениям, так как все расчеты цепей обычно выполняются для действующих ЭДС и токов.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Векторная диаграмма токов и напряжений
Большинство физических процессов имеют динамический характер, когда измеряемые параметры (напряжение электрического поля, сила тока, отклонения маятника или струны) изменяются во времени с определённой частотой повторения. Математический аппарат, применяемый для описания таких колебательных явлений, базируется на использовании гармонических функций, имеющих синусоидальный (или косинусоидальный) вид.
Оказалось, что гармонические колебания можно наглядно описывать в графическом виде с помощью векторных диаграмм (ВД). Колебательный процесс представляется в виде проекции вращающегося вектора на координатную ось (обычно на ось абсцисс Х в прямоугольной системе координат).
Разновидности векторных диаграмм
Основные понятия и обозначения
Колебания — это повторяющийся процесс изменения какой-либо системы (механической, электрической, акустической, тепловой, оптической) вблизи точки равновесия. Типичные примеры:
В общем виде гармоническое колебание описывается формулой:
Когда возникает задача сложения нескольких колебаний, то аналитическое (в виде формул) представление не позволяет судить о действующих соотношениях величин, так как они являются функциями времени. Изображение колебаний (величин A(t)) в виде векторов на плоскости, позволяет добиться наглядности и упрощает анализ количественных параметров системы. При этом колебания совершает проекция на ось абсцисс радиуса-вектора величины A(t) в данный момент времени.
Пускай имеется система, в которой есть два гармонических колебания B1(t), B2(t) с равными частотами ω0. Например, это могут быть токи в электрической цепи или колебания грузиков на пружинках в механической системе. Чтобы получить суммарное колебание, необходимо сложить два выражения: B1(t) = B1 * cos(ω0 * t + φ1) и B2(t) = B2 * cos(ω0 * t + φ2)
Отложим на плоскости вектора B1 и B2 (см. Рис.2). Сумма этих векторов равна:
Видно, что векторное представление позволяет суммировать несколько колебаний с помощью наглядной процедуры сложения векторов.
Типы ВД
Существует два основных типа диаграмм: точные и качественные.
Качественные ВД являются одним из основных инструментов при анализе электрических цепей, наглядно иллюстрирующие положение искомого вектора.
ВД в комплексном представлении
Кроме алгебраической формы, применяется ещё два варианта записи: Z =|Z| * cos(φ)+ i * sin(φ) — тригонометрический, Z = |Z| * e iφ — показательный.
Последний вариант называется формулой Эйлера в честь великого математика, который предложил и обосновал эту формулу в XVIII веке. Комплексное представление гармонических колебаний позволяет упростить сложные тригонометрические вычисления наглядными и менее громоздкими действиями с показательными функциями. Графические ВД, рассмотренные ранее, можно считать аналогом (вариантом) представления гармонических колебаний с помощью комплексных чисел.
Примеры применения
Гармонический осциллятор в механике
Механическая система, будучи выведенная из равновесия, при определённых условиях начинает совершать гармонические колебания под действием возвращающей силы. Такая система называется гармоническим осциллятором. Классические примеры механического осциллятора:
Системы, в которых происходят гармонические колебания, имеют два основных признака:
С помощью универсального уравнения удаётся описать не только механические явления, но и акустические колебания, и электрические (переменный ток, напряжение), а также колебания электронов внутри атомов. Решения данного уравнения представляют собой выражения аналогичные: X(t) = X0 * sin(ω * t +φ0) или X(t) = X0 * cos(ω * t + φ0)
Свободные гармонические колебания без затухания
Из выражений следует, что гармонический осциллятор совершает свободные гармонические колебания с частотой: ω0 = √(k/m). Период колебаний: T = 2*π* √(m/k), где π=3,14. Свободные гармонические колебания в графическом представлении с помощью ВД изображаются вращающимся с частотой ω0 вектором А (Рис.4).
Гармонический осциллятор с затуханием и внешней вынуждающей силой
Гораздо чаще требуется решать задачи, в которых на осциллятор накладывается действие внешней силы, а также имеет место затухание колебаний в связи с наличием силы трения.
Из высшей математики известно, что любую функцию можно представить (разложить) в виде ряда или интеграла Фурье. Значит, решение уравнения может быть сведено к решению с синусоидальной силой:
Метод ВД в данном случае применяется в следующей последовательности:
Чтобы ускорение было направлено к точке равновесия, необходимо выполнение двух условий для выполнения составляющих (радиальной fr и перпендикулярной fp) сил и ускорения по оси вдоль радиуса-вектора по оси ей перпендикулярной. Два условия дают два уравнения:
В результате решения данных уравнений получают выражение для амплитуды колебания при заданной величине вынуждающей силы f:
Из отношения компонент силы fr и fp можно найти тангенс угла, под которым вектор силы на ВД наклонён к радиусу-вектору. Таким образом, будет найден сдвиг фазы колебаний x относительно фазы колебаний внешней силы f.
Метод ВД для расчёта электрических цепей
Чаще всего метод ВД применяется при расчётах электрических цепей. В принципе использование комплексного представления для гармонических колебаний более эффективно, чем классическое построение ВД, так как позволяет анализировать схемы любой сложности, состоящие из резисторов, индуктивностей и конденсаторов. К достоинствам ВД следует отнести доступность в приобретении навыков расчёта, в то время как математический аппарат комплексных чисел требует дополнительных знаний.
Самые распространённые случаи использования ВД для анализа — электрические схемы, в которых применяются пассивные элементы: резисторы, конденсаторы, индуктивности. С помощью ВД получается расчётная формула, при этом сама ВД выполняет роль чертежа-схемы, геометрическим способом иллюстрирующего поведение токов в цепи.
Для того чтобы не использовать комплексное представление, было введено понятие реактивного сопротивления конденсаторов и катушек индуктивностей. Это связано с физическими особенностями протекания переменного тока через эти схемные элементы. Основные формулы, связывающие токи и падения напряжений на элементах:
Напряжение на индуктивности будет:
Формулы для вычисления напряжений на конденсаторе и индуктивности напоминают классический закон Ома за исключением двух отличий:
На основании последних двух формул вводится понятие реактивного сопротивления Z:
ZC = 1/ωC — реактивное емкостное сопротивление.
ZC = ωL — реактивное индуктивное сопротивление.
Преобразование Фурье
Преобразование Фурье — это математическая операция, позволяющая разложить функцию с вещественной переменной на отдельные составляющие — гармонические колебания с разными частотами. Хорошей аналогией в данном случае служит аккорд на музыкальном инструменте, который состоит из нескольких отдельных звуков (нот) определённой частоты. На выходе преобразования получается набор частот (спектр), присутствующих в сигнале и пропорции амплитудных величин.
Преобразование Фурье вещественной функции u(t) задаётся следующей формулой:
где: u(t) — исходный сигнал, U(f) — изображение по Фурье, параметром которого выступает частота.
Эта математическая операция разлагает исходный сигнал на гармонические составляющие (гармоники). При исследованиях частотных спектров применение ВД в некоторых случаях позволяет получить результаты с хорошей точностью простыми средствами. Помимо этого, ВД полезны в иллюстративном плане для качественного понимания формальных вычислений.
Дифракция
Дифракцией в физике называют отклонение световых (электромагнитных) волн от распространения по законам геометрической оптики. При определённых соотношениях длины волны и параметров среды наблюдаются отклонения от прямолинейного распространения, возникает огибание препятствий и проникновение света в область геометрической тени.
Частным случаем является дифракция Фраунгофера (дифракция в параллельных лучах), когда световой источник и точка, где проводятся измерения (наблюдения), бесконечно удалены от препятствия, вызвавшего дифракцию. Как и в предыдущих случаях возникает задача суммирования синусоидальных волн с равными амплитудами, но сдвинутых по фазе на одинаковую величину (предыдущая с последующей). Фазовые сдвиги пропорциональны синусу угла.
Значит, может использоваться метод ВД, в котором каждая синусоида будет представлена вектором. В результате образуется ломаная линия, вписанная в окружность. Переходя к пределу, получится дуга окружности. Суммирующий вектор — это хорда полученной дуги, длина которой рассчитывается по известным геометрическим формулам.
С помощью ВД возможно качественно изучить переход от чисто фраунгоферового случая к более реальному, когда точка наблюдения приближается к щели. Длины векторов становятся неравными, но примерно можно оценить, как изменяется картина, пока расстояние уменьшилось не очень сильно.
Построение ВД напряжений и токов
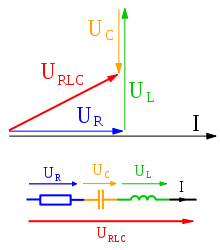
В качестве примера построения ВД рассмотрим последовательную цепочку из сопротивления R, индуктивности L и конденсатора C. Схема приведена на рисунке ниже.
Напряжения на элементах схемы — UR, UL, UC. Ток в цепи — i.
Пускай в цепи протекает синусоидальный ток с частотой ω и с нулевым сдвигом фазы. Для ненулевого сдвига фазы ВД просто повернётся на этот начальный угол, а общий её вид не изменится. Амплитуды напряжений на каждом элементе в форме закона Ома:
Соответствующие этим амплитудам длины векторов наносятся на ВД. При этом каждый вектор наносится с учетом своего фазового сдвига. Суммарный вектор оказался равен U = UR + UL + UC, но это теперь доказано геометрически на диаграмме.
Применив формулы, указанные выше, получим:
Можно вынести за скобки i0 (амплитуда тока — длина вектора i), тогда:
Пользуясь последней формулой, можно вычислять амплитуду синусоидального напряжения. Полученные формулы справедливы для случая обратной задачи, когда требуется найти ток в цепи с известным источником напряжения.
Заключение
Приведённые примеры демонстрируют универсальность применения метода ВД для решения разных физических и технических задач. Синусоидальные, повторяющиеся процессы происходят и в других областях знаний (химических и биологических системах). Наглядность и простота использования хорошо сочетаются на начальном этапе обучения, позволяя в дальнейшем перейти к освоению более сложного аппарата комплексного представления гармонических сигналов.
Что такое векторная диаграмма токов и напряжений? Как построить график

Векторной диаграммой принято называть геометрическое представление изменяющихся по синусоидальному (либо косинусоидальному) закону направленных отрезков — векторов, отображающих параметры и величины действующих синусоидальных токов, напряжений либо их амплитудных величин.
Широкое применение векторные диаграммы нашли в электротехнике, теории колебаний, акустике, оптике и т.д.
Различают 2-х вида векторных диаграмм:
Интересное видео о векторных диаграммах смотрите ниже:
Точные изображаются по результатам численных расчетов при условии соответствия масштабов действующих значений. При их построении можно геометрически определить фазы и амплитудные значения искомых величин.
Они являются одним из основных средств анализа электрических цепей, позволяя наглядно иллюстрировать и качественно контролировать ход решения задачи и легко установить квадрант, в котором располагается искомый вектор.

Векторы, изображаемые на такой диаграмме, характеризуются равновеликой угловой частотой ω. В виду чего при вращении их взаимное расположение не изменяется.
Ещё одно полезное видео о векторных диаграммах:
Поэтому при изображении векторных диаграмм один вектор можно направить произвольным образом (например, по оси ОХ).
А остальные — изображать по отношению к исходному под различными углами, соответственно равными углам сдвига фаз.
Таким образом, векторная диаграмма дает отчетливое представление об опережении либо отставании различных электрических величин. 
Допустим у нас есть ток, величина которого изменяется по некоторому закону:
i = Im sin (ω t + φ).
С начала координат 0 под углом φ проведем вектор Im, величина которого соответствует Im. Его направление выбирается так, чтобы с положительным направлением оси OX вектор составлял угол — соответствующий фазе φ.
В основном векторные диаграммы изображают для действующих значений, а не амплитудных. Векторы действующих значений количественно отличаются от амплитудных значений — масштабом, поскольку:
I = Im /√2.

Основным преимуществом векторных диаграмм называют возможность простого и быстрого сложения и вычитания 2-х параметров при расчете электроцепей.
Векторная диаграмма
Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов. Векторные диаграммы широко применяются в электротехнике, акустике, оптике, теории колебаний и так далее.
Содержание
Векторные диаграммы и комплексное представление
Тогда вектор длиной A, вращающийся в комплексной плоскости с постоянной угловой скоростью ω с начальным углом φ0 запишется как комплексное число
а его действительная часть
-есть гармоническое колебание с циклической частотой ω и начальной фазой φ0.
Хотя, как видно уже из вышесказанного, векторные диаграммы и комплексное представление колебаний теснейшим образом связаны и по сути представляют собой варианты или разные стороны одного и того же метода, они, тем не менее, обладают своими особенностями и могут применяться и по отдельности.
Примеры применения
Механика; гармонический осциллятор
Разберем два основных случая простого применения векторных диаграмм в механике (как замечено выше, также применимых к гармоническому осциллятору не только механической, но любой природы): осциллятор без затухания и без внешней силы и осциллятор с (линейным) затуханием (вязкостью), и внешней вынуждающей силой.
Свободные гармонические колебания без затухания
Идея, в механической формулировке, заключается в достраивании одномерного движения до двумерного таким образом, чтобы вектор скорости имел ту же компоненту по оси x, что и в одномерном случае, и был перпендикулярен радиус-вектору (проекция которого на ось x и есть координата x водномерной системе).
Если двумерная скорость (на диаграмме) не меняется по величине (по модулю), то можно показать, что ускорение направлено также под прямым углом к скорости и направлено в точности противоположно радиус-вектору (центростемительное ускорение).
Что касается соотношения величин векторов, то исходя из довольно очевидного геометрически факта, что конец любого вектора длиной L, вращающегося вокруг своего начала с угловой скоростью ω, равна ωL, и предполагая, что движение на двумерной диаграмме чисто вращательное, легко понять, что

(Таким образом мы получили, по ходу дела, и теорему о центростремительном ускорении [2] ).
Естественным расширением возвращающей силы одномерного осциллятора
до двумерной, удовлетворяющей условию совпадения x-компоненты силы с одномерной, будет
Тогда видим, что можно подобрать скорость вращения так, чтобы все векторы оставались неизменными по величине, и только вращались с угловой скоростью ω. А именно, если 
(При этом длину вектора 

где 

Гармонический осциллятор с затуханием и внешней вынуждающей силой
Аналогично можно рассмотреть решение уравнения движения гармонического осциллятора со внешней вынуждающей силой f:
Поскольку практически любая [3] сила f может быть разложена в ряд или интеграл Фурье, то есть представлена как сумма (дискретная сумма или интеграл) синусоидальных сил, задача сводится к задаче с синусоидальной силой
(Вследствие линейности уравнения движения, решение для суммы нескольких или даже бесконечного числа синусоидальных f будет суммой решений для каждого из этих f). (Кроме того, и случай чисто синусоидальной силы (а даже не суммы разных синусоид) может быть важен сам по себе).
При этом пытаемся подобрать эти векторы так, чтобы двумерное движение сводилось к чистому вращению.
Для этого надо потребовать, чтобы суммарная сила, действующая на массу осциллятора (являющуюся материальной точкой), была направлена всегда к одной и той же точке (центру вращения), а по величине равнялась величине центростремительного ускорения, умноженного на массу.
Исходя из этих условий получаем уравнение на соотношение модулей векторов (соответствующих, очевидно, амплитудам колебания соответствующих одномерных величин), а также и на их углы (соответствующие фазам одномерных колебаний).
Разумно, исходя из симметрии, предположить, что вращение должно происходить относительно начала координат (точки равновесия).
Тогда ускорение должно быть направлено к этой точке (ведь мы имеем в виду правильное равномерное вращение), а значит, имеем два условия, если рассмотрим компоненты сил и ускорения по оси, соответствующей радиус вектору и по оси перпендикулярной ей. Эти два условия записываются как уравнения
Разрешая каждое из этих двух уравнений относительно компоненты силы f, а затем возводя каждое в квадрат и сложив, имея в виду по теореме Пифагора 
то есть выражение для амплитуды колебания при заданной амплитуде вынуждающей силы f.
Как видим, исследование колебаний под действием вынуждающей синусоидальной силы (из которого в числе прочего получаются условия резонанса итд итп) для гармонического осциллятора вполне успешно осуществляется методом векторных диаграмм. Впрочем, для исследования других вопросов, таких, как получение затухающего решения в отсутствие внешней вынуждающей силы, такой метод не слишком удобно применим. [4]
Расчет электрических цепей
Затем в эти уравнения подставляют синусоидальный ток:
Заметим, что формулы очень похожи на обычный закон Ома
за исключением двух моментов: 1) если обычное (называемое в данном контексте активным) сопротивление R не вызывает изменения фазы напряжения по сравнению с током (они синфазны), то напряжение на конденсаторе запаздывает по фазе относительно тока на 90°, а на индуктивности напряжение опережает ток по фазе на те же 90°; 2) коэффициент, на который домножается ток, чтобы получить напряжение, как раз и называемый реактивным сопротивлением зависит и у конденсатора, и у индуктивности от частоты тока (и зависит разным, обратным, образом).
Таким образом, мы знаем, как изобразить на векторной диаграмме напряжение на конденсаторе, индуктивности или резисторе, если известен ток (то есть его вектор уже нарисован). А именно: для конденсатора мы должны умножить (масштабировать) вектор, изображающий ток, на коэффициент 

Совершенно аналогично можно построить на векторной диаграмме вектор, изображающий ток, если мы знаем вектор, изображающий напряжение. (Очевидно, просто умножать придется на обратные приведенным выше числа, и поворачивать вектор в противоположную сторону).
Когда это ясно, можно рассмотреть конкретно типичные задачи для параллельного и последовательного соединения элементов.
Последний вариант построения векторной диаграммы (для последовательно соединенных резистора, индуктивности и конденсатора) приведен на рисунке.
Подробно
В последовательную цепь (как на рисунке) включены резистор сопротивлением R, конденсатор емкостью C и катушка индуктивностью L. Обозначим напряжение на каждом из этих элементов соответственно UR,UC,UL, а ток через цепь (одинаковый для каждого элемента из-за их последовательного включения) обозначим I.
Напряжение на концах цепи (которое мы обозначим как URLC) будет суммой напряжений на каждом элементе:
Полагаем (по условию задачи [11] ), что ток в цепи синусоидальный, и изображаем его на векторной диаграмме (верхняя часть рисунка) как горизонтальный вектор длиной, равной амплитуде тока (это означает, что мы принимаем начальную фазу тока за ноль; если она не ноль в реальном случае, то такой случай сводится к нашему сдвигом начала отсчета времени или поворотом всей векторной диаграммы целиком на угол начальной фазы, что ничего не меняет в последующих рассуждениях).
Полагаем (также по условию задачи), что частота тока (а следовательно и напряжений) задана и равна ω.
Напряжение на каждом из элементов цепи вычисляется исходя из его активного или реактивного сопротивления, а именно амплитуды напряжений, соответствующие длинам векторов, которыми эти напряжения изображаются на диаграмме, равны:


Далее складываем UR,UC,UL по правилам сложения векторов, то есть, как на рисунке, строим цепочку векторов (ломаную), где каждый следующий прибавляемый вектор строится так, чтобы его начало совпадало с концом предыдущего.
Вектором суммы оказывается, как мы и полагали выше
однако теперь мы видим этот вектор на диаграмме конкретно.
Длина этого вектора оказывается длиной гипотенузы прямоугольного треугольника со сторонами |UR| и ||UL|-|UC|| (на рисунке изображен случай, когда |UL| > |UC|, однако это никак не скажется на последующих вычислениях).
Следовательно, по теореме Пифагора,
а подставляя длины векторов UR, UL, UC из формул, выписанных выше, имеем
где I0 обозначена амплитуда тока (равная длине вектора I); вынося I0 из-под корня, имеем:
то есть аналитическое выражение для амплитуды напряжения на цепи.
Преобразование Фурье
Векторные диаграммы могут быть использованы применительно к рядам Фурье и преобразованию Фурье (с физической точки зрения это по большей мере интерпретируется как исследование частотного спектра тех или иных процессов).
В некоторых частных случаях применение векторных диаграмм позволяет достаточно элементарными средствами получить в этой области довольно нетривиальные точные результаты. Ценность такого применения в современном контексте, видимо, не слишком велика, поскольку все эти результаты могут быть воспроизведены более стандартными и общими аналитическими приемами («без использования чертежей»), однако, по-видимому, способ векторных диаграмм может тут быть полезен в педагогическом плане, а также для популяризации, и, возможно, иногда для каких-то инженерных применений.
Кроме того, векторные диаграммы могут быть в этой области несомненно полезны в качестве иллюстрации, а также для лучшего качественного понимания формальных результатов и, вероятно, иногда для получения каких-то оценочных соотношений.
Сложение двух синусоидальных колебаний
Собственно, можно сказать, что рассмотрение с помощью векторных диаграмм может в числе прочего и помочь запомнить (или восстановить в памяти) соответствующие тригонометрические формулы.
Фурье-образ прямоугольного сигнала
Имея в виду, что решение всех задач, обозначенных во вводном замечании, формально по сути одинаково, сосредоточимся на том, чтобы наметить путь решения той из них, которая имеет более прозрачный физический смысл. А именно на задаче определить форму сигнала (явный вид функцию от времени), представляющего собой сумму сумму синусоид, равных по амплитуде и равноудаленных по частоте (а начальная фаза каждой из этих синусоид пусть равна нулю).
Каждая из таких синусоид, очевидно, изображается на векторной диаграмме вектором одной и той же длины. В начальный момент времени (t=0) все эти векторы горизонтальны и направлены вправо. В последующие моменты времени угол поворота каждого вектора линейно зависит от его номера.
Длину этого вектора также нетрудно вычислить из элементарных геометрических соображений.
Дифракция
Довольно интересно, что метод векторных диаграмм позволяет качественно исследовать переход от фраунгоферова случая к более общему (при приближении экрана наблюдения к щели). (Тогда длины складываемых векторов перестают быть одинаковыми, однако качественно можно понять, как меняется картина, особенно пока расстояние до экрана уменьшилось не слишком сильно).