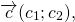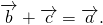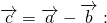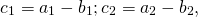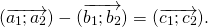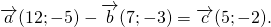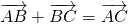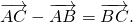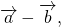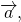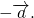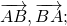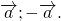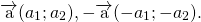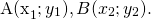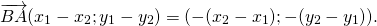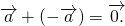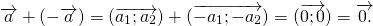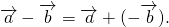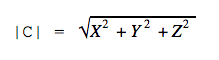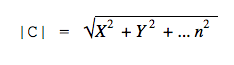Что такое вектор разности
Сложение и вычитание векторов
Существование: Имеем два следующих случая:
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сумма векторов. Сложение векторов. Правило треугольника
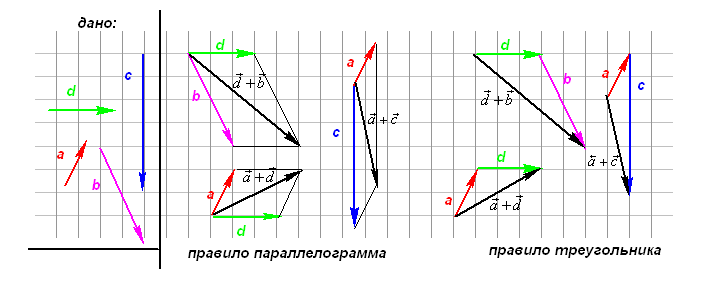
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
\( \vec + \vec = \left( <
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора \( \overrightarrow \) выполняется равенство
Для произвольных точек \( A,\ B\ и\ C \) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Разность векторов. Вычитание векторов
Длина нулевого вектора равна нулю:
\( \left| \vec <0>\right| = 0 \)
Умножение вектора на число
Определение Произведением вектора \( \overrightarrow
Длина вектора \( \overrightarrow
Векторы \( \overrightarrow
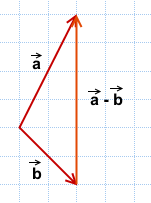
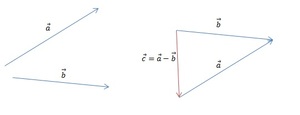
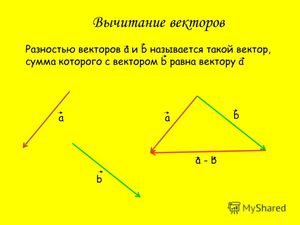
Разность векторов
Разность векторов
— это такой вектор
который в сумме с вектором b даёт вектор a:
На основе определения находим координаты вектора
Как построить разность двух векторов?
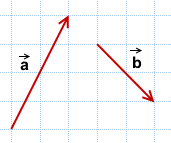
правило построения разности двух векторов
Чтобы построить вектор, равный разности векторов
надо отложить оба вектора от одной точки. Разность векторов — вектор, проведённый от конца вычитаемого b к концу уменьшаемого a.
Противоположные векторы — это противоположно направленные векторы одинаковой длины.
Вектор, противоположный вектору
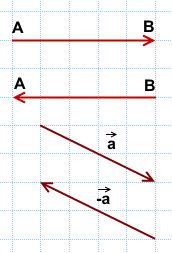
Свойства противоположных векторов:
1) Противоположные векторы имеют противоположные координаты:
2) Сумма противоположных векторов равна нулевому вектору:
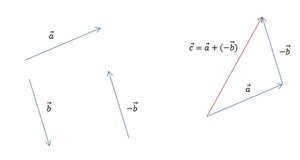
2 способ построения разности векторов

можно к вектору a прибавить вектор, противоположный вектору b:
То есть вычитание векторов заменяем сложением уменьшаемого с вектором, противоположным вычитаемому.
Операции с векторами
Как сложить и перемножить векторы (и зачем).
Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.
Напомним основные мысли:
С векторами можно совершать некоторые математические операции. Вот о них и поговорим.
Правильно — векторы
Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».
Сложение
Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.
Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).
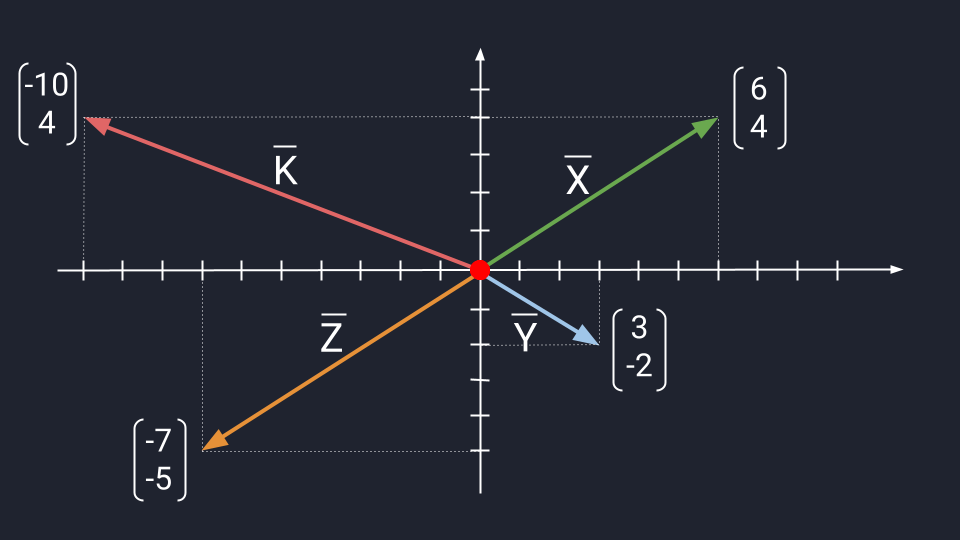
Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.
Предположим, нам нужно сложить векторы X и Y.
X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)
Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.
Например, вот сложение векторов с пятью координатами:
Интуитивное изображение сложения
Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.
Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.
Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.
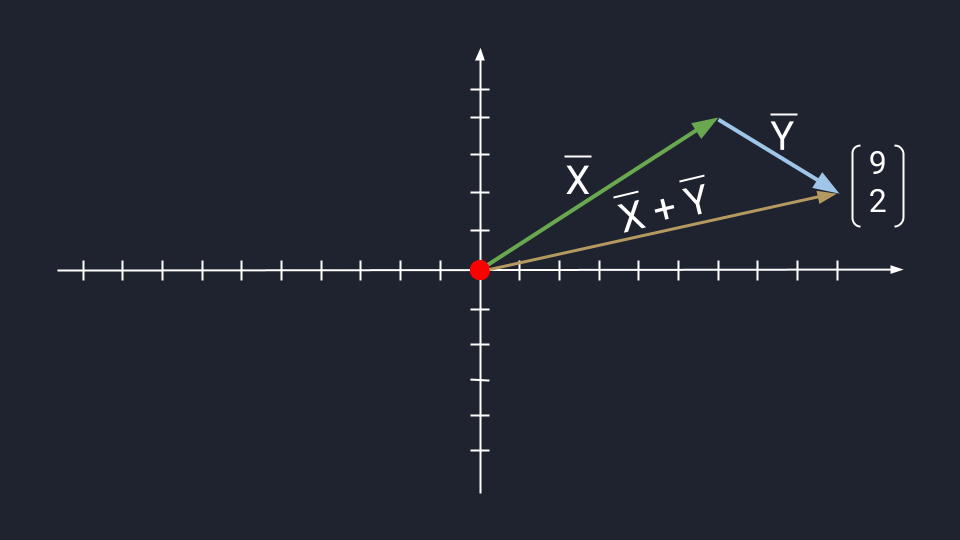
Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.
Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.
Вычитание
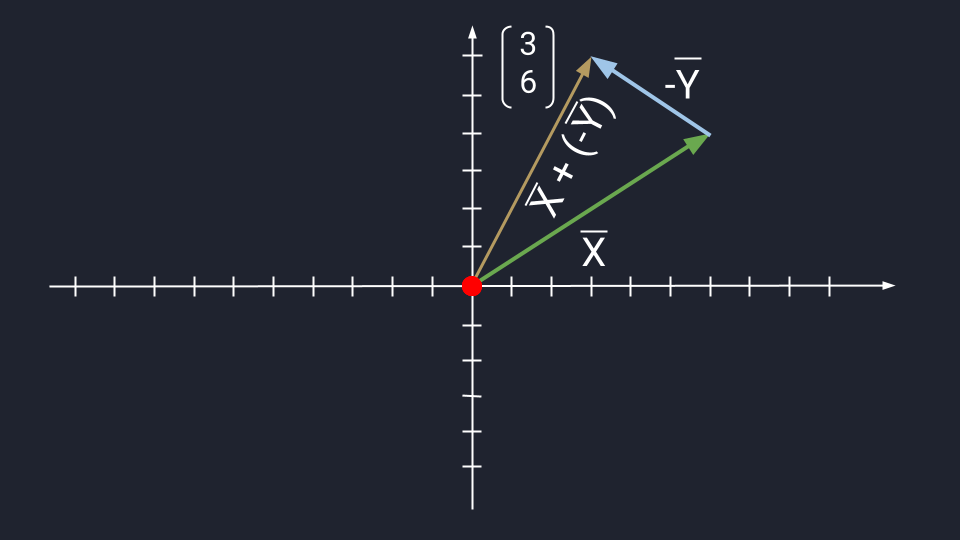
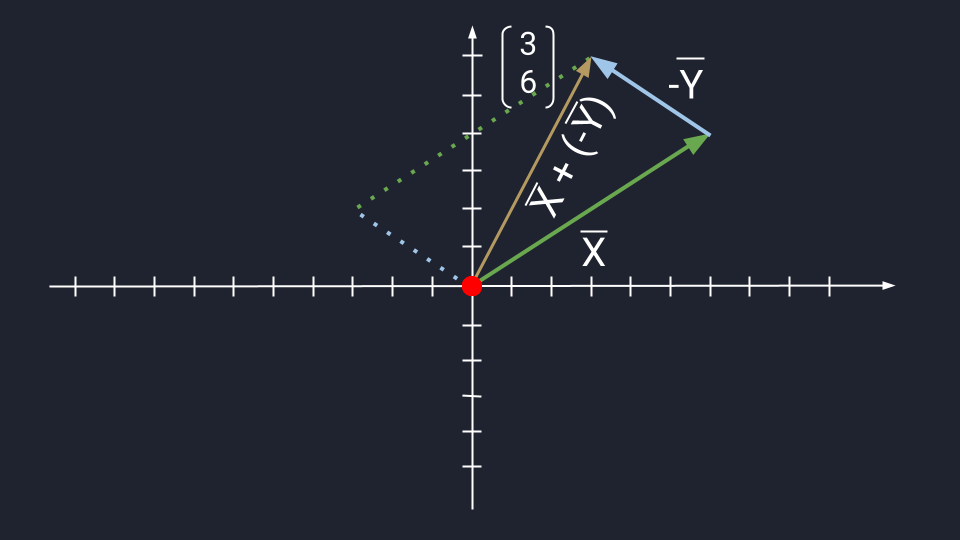
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)
Дальше используются правила сложения. Пошагово это выглядит так:
Теперь посмотрим, как выглядит вычитание векторов на графике:
Длина вектора
Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.
Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:
X = 6 − 2 = 4
Y = 5 − 2 = 3
Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:
|C|2 = 42 + 32 = 25
|C| = √25 = 5 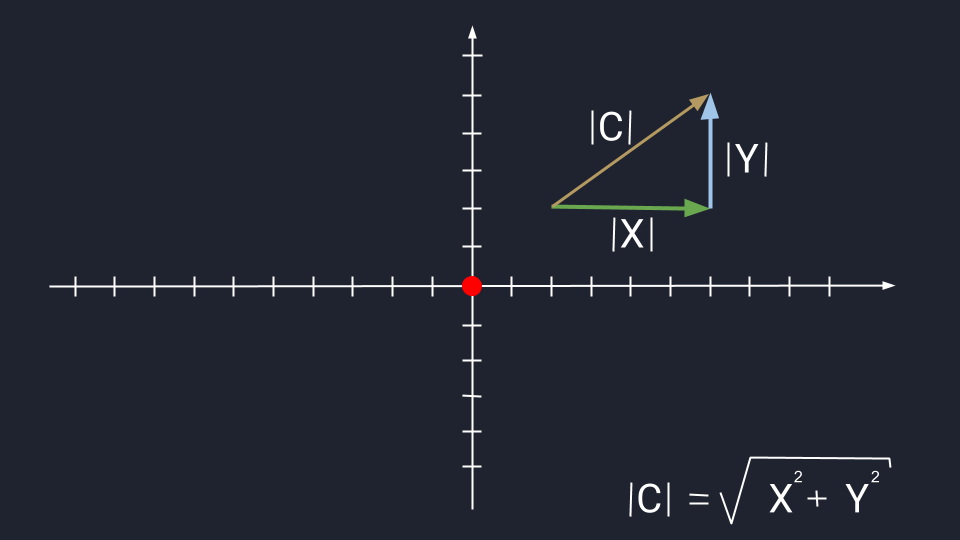
Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.
В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.
Умножение и деление вектора на число
Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.
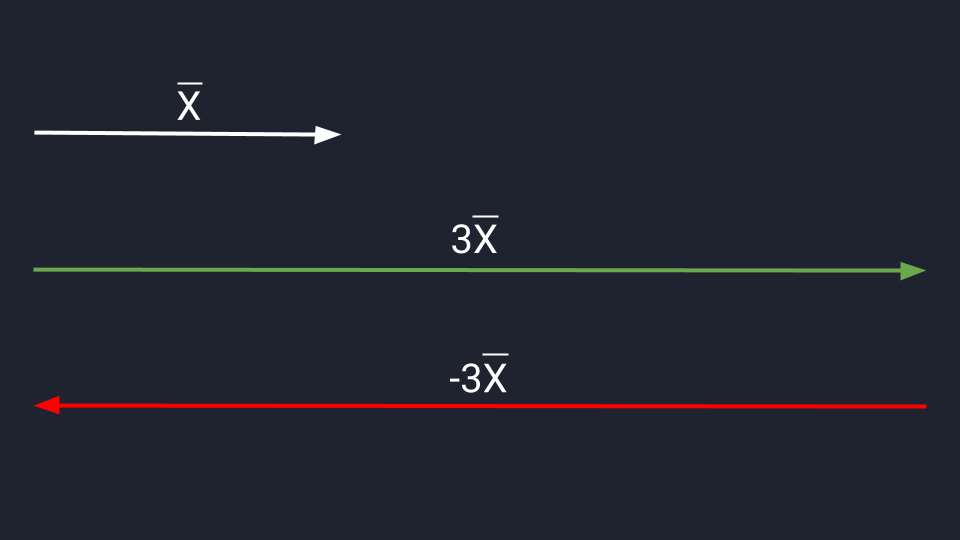
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.
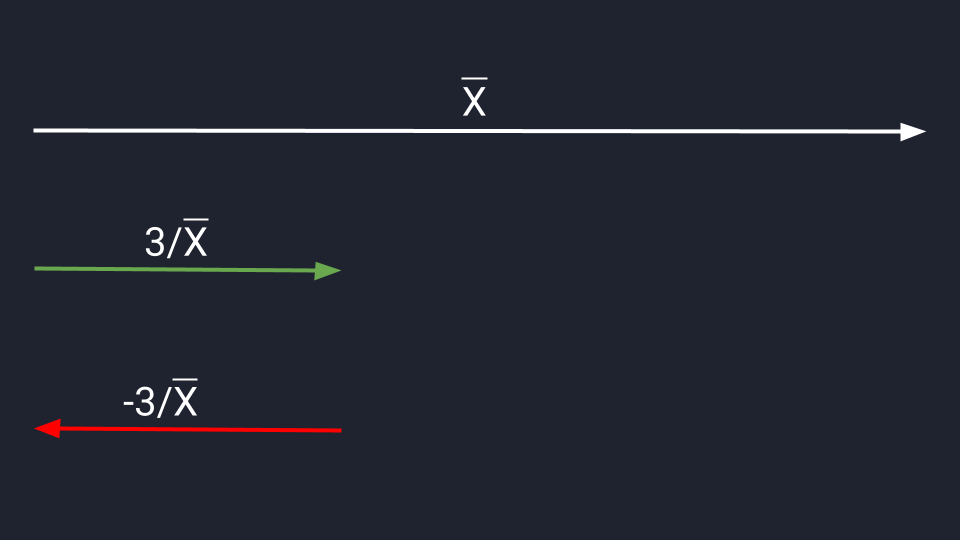
Да вроде несложно!
Пока ничего сложного. Но если углубляться, вы узнаете, что:
Что дальше
В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.
Определение разности двух векторов
[block >
Определения векторной математики
Введём главные определения, используемые при выполнении линейных операций.
Аналитический метод
Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.
Для двухмерного пространства и векторных величин a <a₁; a₂> и b <b₁; b₂> расчёты будут иметь следующий вид: c <c₁; c₂> = <a₁ — b₁; a₂ — b₂>.
В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a <a₁; a₂; a₃> и b <b₁; b₂; b₃> координаты разности будут также получены попарным вычитанием: c <c₁; c₂; c₃> = <a₁ — b₁; a₂ — b₂; a₃ — b₃>.
Вычисление разности графически
Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:
[block > Результат операции вычитания показан на рисунке ниже.
Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:
Результат такого решения изображён на рисунке:
Решение задач
Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.
Задача 1. На плоскости заданы 4 точки: A (1; —3), B (0; 4), C (5; 8), D (—3; 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.
Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1; —3), а концом — B (0; 4). Рассчитаем координаты направленного отрезка:
Аналогичный расчёт выполняется для CD:
Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид <c₁; c₂> = <a₁ — b₁; a₂ — b₂>. Для конкретного случая можно записать:
Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.
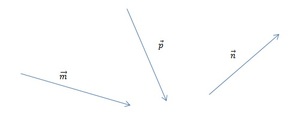
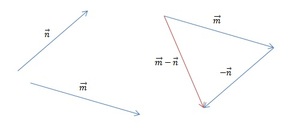
[block > Задача 2. На рисунке изображены векторы m, n и p.
Необходимо построить для них разности: p — n; m — n; m — n — p. Выяснить, какая из них обладает наименьшим модулем.
Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.
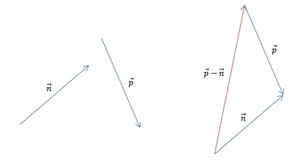
Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.
Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:
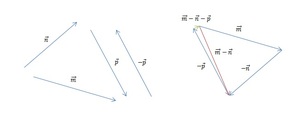
[block > Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:
Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).
Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.
[block > [block >
Физика
Тестирование онлайн
Вектор
Если начало вектора совпадает с его концом, получим нулевой вектор.
Два вектора являются равными, если их длина одинаковая и они имеют одинаковое направление. Они совмещаются при переносе.
На рисунке только вектор a равен вектору b. Вектор c им не равен, так как направлен в противоположную сторону
Проекция вектора
Спроецируем вектор перемещения на ось Ox и на ось Oy. Для того, чтобы получить проекцию необходимо из координаты конца вектора отнять координату начала. На ось ОХ: sx=x-x0, на ось ОУ: sy=y-y0.
Частные случаи, когда проекция на ось Ox или Oy нулевая.

Сумма составляющих вектора по осям равна данному вектору, т.е.
Сложение векторов
Правило треугольника: от конца первого вектора отложить второй вектор, тогда их суммой будет вектор, начало которого совпадает с началом первого вектора, а конец с концом второго вектора.
Рассмотрим правила на примерах.
Вычитание векторов
Упражнения
Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть численно равной одному из составляющих векторов?
Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть меньше меньшего из составляющих векторов?