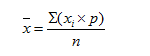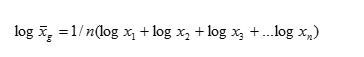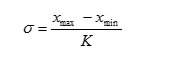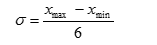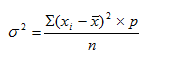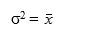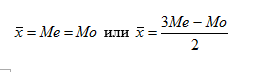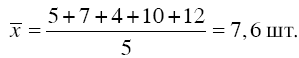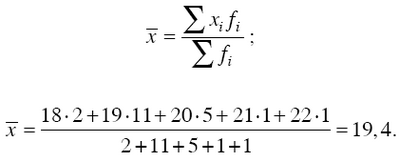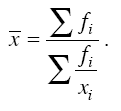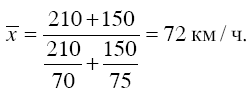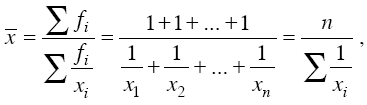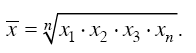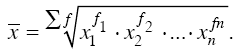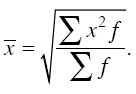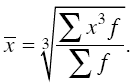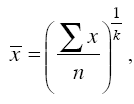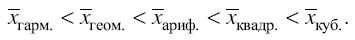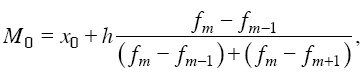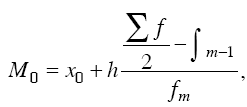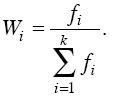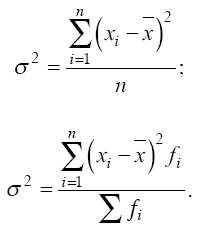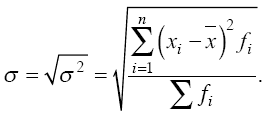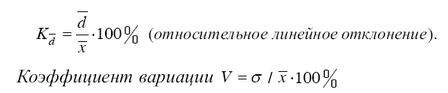Что такое варианта в статистике
Сводка и группировка статистических данных
3.3. Ряды распределения: виды, правила построения, графическое изображение
Ряды распределения делятся на атрибутивные и вариационные, в зависимости от признака, положенного в основу группировки. Если признак качественный, то ряд распределения называется атрибутивным. Примером атрибутивного ряда является распределение предприятий и организаций по формам собственности (см. табл. 3.1).
Если признак, по которому строится ряд распределения, количественный, то ряд называется вариационным.
Вариационные ряды бывают дискретными и интервальными. У дискретных рядов (табл. 3.7) варианты выражены конкретными числами, чаще всего целыми.
| Время работы в компании, полных лет (варианты) | Число работающих | |
|---|---|---|
| Человек (частоты) | в % к итогу (частости) | |
| до года | 15 | 11,6 |
| 1 | 17 | 13,2 |
| 2 | 19 | 14,7 |
| 3 | 26 | 20,2 |
| 4 | 10 | 7,8 |
| 5 | 18 | 13,9 |
| 6 | 24 | 18,6 |
| Итого | 129 | 100,0 |
Если признак принимает ограниченное число значений, обычно не больше 10, строят дискретные ряды распределения. Если вариант больше, то дискретный ряд теряет свою наглядность; в этом случае целесообразно использовать интервальную форму вариационного ряда. При непрерывной вариации признака, когда его значения в определенных пределах отличаются друг от друга на сколь угодно малую величину, также строят интервальный ряд распределения.
3.3.1. Построение дискретных вариационных рядов
Рассмотрим методику построения дискретных вариационных рядов на примере.
Пример 3.2. Имеются следующие данные о количественном составе 60 семей:
| 2 3 3 1 4 2 3 3 1 5 2 4 3 2 2 1 2 3 4 5 |
| 2 2 1 3 4 3 3 3 6 6 3 3 6 1 3 4 3 4 4 5 |
| 3 3 2 2 1 3 2 5 5 2 4 3 6 1 2 2 3 1 3 4 |
Для того чтобы получить представление о распределении семей по числу их членов, следует построить вариационный ряд. Поскольку признак принимает ограниченное число целых значений строим дискретный вариационный ряд. Для этого сначала рекомендуется выписать все значения признака (число членов в семье) в порядке возрастания (т.е. провести ранжирование статистических данных):
| 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 |
| 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 |
| 3 3 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 6 6 6 |
| Число членов семьи (х) | Число семей (y) |
|---|---|
| 1 | 8 |
| 2 | 14 |
| 3 | 20 |
| 4 | 9 |
| 5 | 5 |
| 6 | 4 |
| Итого | 60 |
3.3.2. Построение интервальных вариационных рядов
Покажем методику построения интервальных вариационных рядов распределения на следующем примере.
Пример 3.3. В результате статистического наблюдения получены следующие данные о средней величине процентной ставки 50 коммерческих банков (%):
| 14,7 | 19,0 | 24,5 | 20,8 | 12,3 | 24,6 | 17,0 | 14,2 | 19,7 | 18,8 |
| 18,1 | 20,5 | 21,0 | 20,7 | 20,4 | 14,7 | 25,1 | 22,7 | 19,0 | 19,6 |
| 19,0 | 18,9 | 17,4 | 20,0 | 13,8 | 25,6 | 13,0 | 19,0 | 18,7 | 21,1 |
| 13,3 | 20,7 | 15,2 | 19,9 | 21,9 | 16,0 | 16,9 | 15,3 | 21,4 | 20,4 |
| 12,8 | 20,8 | 14,3 | 18,0 | 15,1 | 23,8 | 18,5 | 14,4 | 14,4 | 21,0 |
Как видим, просматривать такой массив данных крайне неудобно, кроме того, не видно закономерностей изменения показателя. Построим интервальный ряд распределения.
Число интервалов на практике часто задается самим исследователем исходя из задач каждого конкретного наблюдения. Вместе с тем его можно вычислить и математически по формуле Стерджесса
Для нашего примера получим: n = 1 + 3,322lgN = 1 + 3,322lg50 = 6,6 » 7.
Для нашего примера
Интервалы вариационного ряда наглядны, если их границы имеют «круглые» значения, поэтому округлим величину интервала 1,9 до 2, а минимальное значение признака 12,3 до 12,0.
Интервалы, как правило, записывают таким образом, чтобы верхняя граница одного интервала являлась одновременно нижней границей следующего интервала. Так, для нашего примера получим: 12,0-14,0; 14,0-16,0; 16,0-18,0; 18,0-20,0; 20,0-22,0; 22,0-24,0; 24,0-26,0.
Подобная запись означает, что признак непрерывный. Если же варианты признака принимают строго определенные значения, например, только целые, но их количество слишком велико для построения дискретного ряда, то можно создать интервальный ряд, где нижняя граница интервала не будет совпадать с верхней границей следующего интервала (это будет означать, что признак дискретный). Например, в распределении работников предприятия по возрасту можно создать следующие интервальные группы лет: 18-25, 26-33, 34-41, 42-49, 50-57, 58-65, 66 и более.
Кроме того, в нашем примере мы могли бы сделать первый и последний интервалы открытыми, т.д. записать: до 14,0; 24,0 и выше.
| Ставка банка % (варианты) | |||
|---|---|---|---|
| 12,3 | 17,0 | 19,9 | 23,8 |
| 12,8 | 17,4 | 20,0 | 24,5 |
| 13,0 | 18,0 | 20,0 | 24,6 |
| 13,3 | 18,1 | 20,4 | 25,1 |
| 13,8 | 18,5 | 20,4 | 25,6 |
| 14,2 | 18,7 | 20,5 | |
| 14,3 | 18,8 | 20,7 | |
| 14,4 | 18,9 | 20,7 | |
| 14,7 | 19,0 | 20,8 | |
| 14,7 | 19,0 | 21,0 | |
| 15,1 | 19,0 | 21,0 | |
| 15,2 | 19,0 | 21,1 | |
| 15,3 | 19,0 | 21,4 | |
| 16,0 | 19,6 | 21,9 | |
| 16,9 | 19,7 | 22,7 | |
При подсчете частот может возникнуть ситуация, когда значение признака попадет на границу какого-либо интервала. В таком случае можно руководствоваться правилом: данная единица приписывается к тому интервалу, для которого ее значение является верхней границей. Так, значение 16,0 в нашем примере будет относиться ко второму интервалу.
Результаты группировки, полученные в нашем примере, оформим в таблице.
| Краткая ставка, % | Количество банков, ед. (частоты) | Накопленные частоты |
|---|---|---|
| 12,0-14,0 | 5 | 5 |
| 14,0-16,0 | 9 | 14 |
| 16,0-18,0 | 4 | 18 |
| 18,0-20,0 | 15 | 33 |
| 20,0-22,0 | 11 | 44 |
| 22,0-24,0 | 2 | 46 |
| 24,0-26,0 | 4 | 50 |
| Итого | 50 | — |
В процессе группировки данных при построении вариационных рядов иногда используются неравные интервалы. Это относится к тем случаям, когда значения признака подчиняются правилу арифметической или геометрической прогрессии или когда применение формулы Стерджесса приводит к появлению «пустых» интервальных групп, не содержащих ни одной единицы наблюдения. Тогда границы интервалов задаются произвольно самим исследователем исходя из здравого смысла и целей обследования либо по формулам. Так, для данных, изменяющихся в арифметической прогрессии, величина интервалов вычисляется следующим образом:
Порядок расчетов границ неравных интервалов для данных, изменяющихся приблизительно в арифметической прогрессии, показан в табл. 3.15.
Для показателей, приблизительно изменяющихся в геометрической прогрессии, величину интервалов можно вычислить по формуле
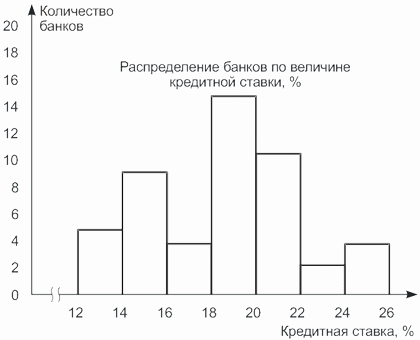
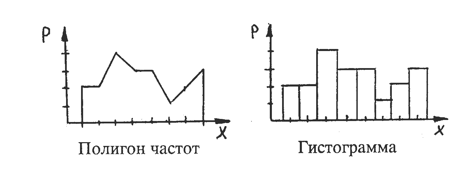
Для графического изображения интервального ряда используют гистограмму, имеющую вид многоступенчатой фигуры, состоящей из прямоугольников. По оси абсцисс откладывают значения границ интервалов. Сами интервалы будут являться основаниями прямоугольников. Высота прямоугольников соответствует частоте или частости интервалов, которые откладываются по оси ординат.
По данным таблицы, приведенной в примере 3.3, построим гистограмму (рис. 3.2).
При неравных интервалах у гистограммы распределения высотами прямоугольников будут являться показатели плотности распределения, рассчитываемые как частное от деления частоты интервала на его величину.
Зависимость между значениями признака и накопленными частотами показывают особые графики, называемые кумулятой и огивой распределения.
В случае интервального ряда при построении кумуляты по оси абсцисс отмечают границы интервальных групп, накопленные частоты по оси ординат относят к верхним границам интервалов.
По данным таблицы, приведенной в примере 3.3, построим кумуляту распределения для интервального ряда (рис. 3.2).
Если у кумулятивной кривой поменять местами ось абсцисс с осью ординат, получим график, называемый огивой распределения (рис. 3.4).
Вариационные ряды — помощь в оценке распределения явлений по величине признаков
Вариационный ряд (frequency table)- ранжированный ряд распределения по величине какого-либо признака. Этот признак носит название варьирующего, а его отдельные числовые значения называются вариантами и обозначаются через «х». Число, показывающее, сколько раз данная варианта встречается в вариационном ряду, называется частотой и обозначается через «р».
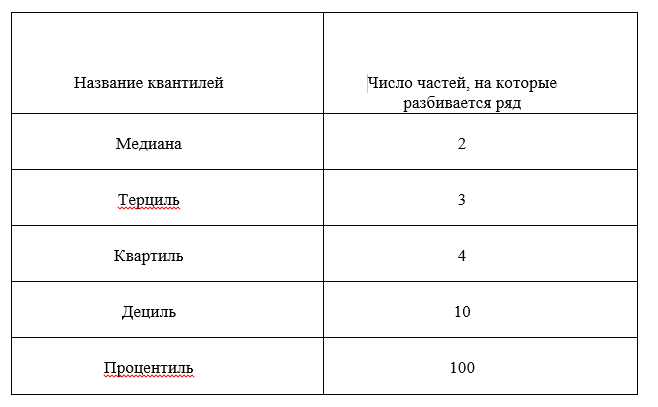
Вариационный ряд можно разбивать на отдельные (по возможности равные) части, которые называются квантилями (quantile). Наиболее часто употребляемые квантили представлены в таблице:
Рис. 1 Этапы описания (обобщения) количественного признака
Виды вариационных рядов
Вариационные ряды могут быть следующих видов:
Графическое изображение вариационных рядов
где х — варианты, р — частоты.
Основные характеристики вариационного ряда
Такие характеристики зависят от оцениваемых показателей:
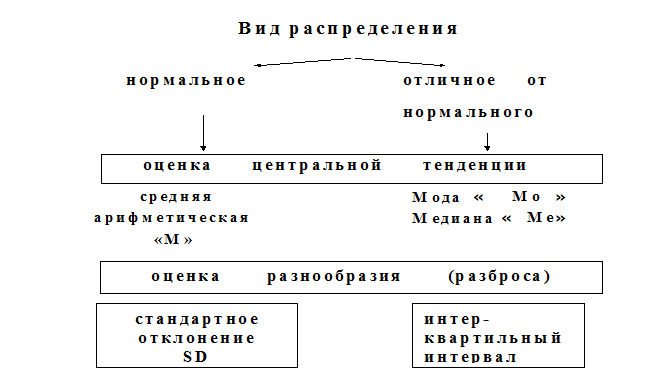
1). Показатели, характеризующие центральную тенденцию (central tendency) или уровень ряда: средние величины или меры расположения (собственно средние и структурные средние).
2). Показатели, характеризующие разнообразие (рассеяние, вариацию, разброс) (spread) признака: стандартное отклонение, дисперсия, размах, интерквартильный интервал.
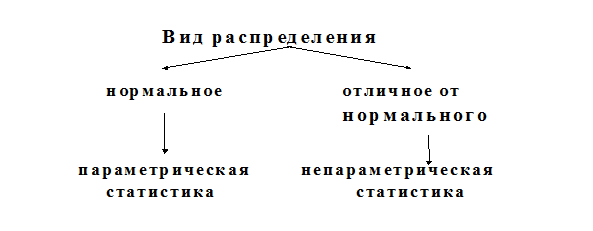
Выбор характеристик центральной тенденции и разнообразия признака прежде всего зависит от вида распределения. В случае нормального распределения используют показатели параметрической статистики, в случае распределения, отличного от нормального и при неизвестном виде распределения применяют показатели непараметрической статистики.
Средние величины
Средняя величина — обобщающий коэффициент, который характеризует наиболее типичный размер определенного признака в целом для совокупности или для отдельных ее частей. Расчет средних величин имеет смысл только для качественно однородной совокупности, в связи с этим в одной совокупности может быть столько средних, на сколько однородных групп она может быть разбита.
Виды средних величин
Средняя арифметическая(mean) — применяется, если варианты возрастают (убывают) в арифметической прогрессии.
х — средняя арифметическая;
р — частота встречаемости варианты;
n — число наблюдений
Свойства средней арифметической:
— носит обобщающий характер;
— имеет абстрактное значение;
— алгебраическая сумма отклонений отдельных вариант от средней равна 0 (сущность средней и способ проверки правильности расчета средней);
— сумма квадратов отклонений отдельных вариант от средней меньше суммы квадратов отклонений вариант от любой другой величины, неравной средней;
— сумма произведений отдельных вариант на свои частоты равна произведению средней на число наблюдений (единство суммарного действия и способ проверки правильности расчета средней);
— если частоту всех вариант пропорционально изменить, то средняя арифметическая от этого не изменится.
Средняя геометрическая — вычисляется, если варианты возрастают (убывают) в геометрической прогрессии.
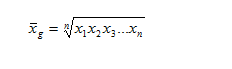
Структурные средние
Мода (Мо) (mode)- наиболее часто встречающаяся в вариационном ряду варианта.
Медиана (Me)(median) — варианта, которая делит вариационный ряд на две равные
части. Медиана используется:
Характеристики разнообразия вариационного ряда
— приблизительный расчет стандартного отклонения по амплитуде:
где К — коэффициент Ермолаева, рассчитывается по специальной таблице с учетом числа наблюдений (см. приложение).
При числе наблюдений больше 30:
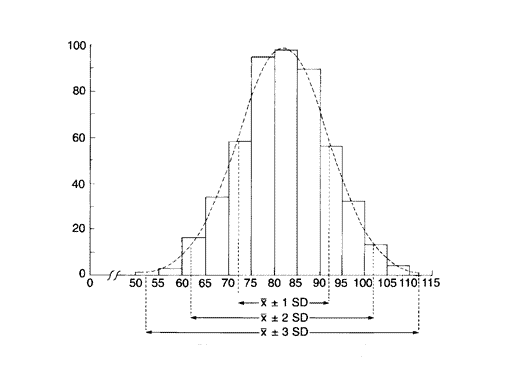
Стандартное отклонение наиболее часто используется при определении нормы и патологии, в основе которого лежит «правило трех сигм», справедливое только для нормального распределения.
Сводная таблица формул
для нахождения средних значений и мер рассеяния
«Правило трех сигм»
68.3 % всех вариант отклоняются от своей средней не более, чем на s
95.4% вариант находятся в пределах X ± 2s
99.7% вариант находятся в пределах X ± 3s
Отклонение параметра от его средней арифметической в пределах s расценивается как норма, субнормальным считается отклонение в пределах ± 2s и патологическим — сверх этого предела, т.е. > ± 2s» (рис. )
Рис.3 Правило «трех сигм» ( SD – стандартное отклонение).
При распределении Пуассона дисперсия равна средней:
Коэффициент вариации используется при сравнении вариационных рядов, имеющих различную размерность, или одной размерности, но обладающими резкими различиями в своих значениях, затрудняющими их сопоставление.
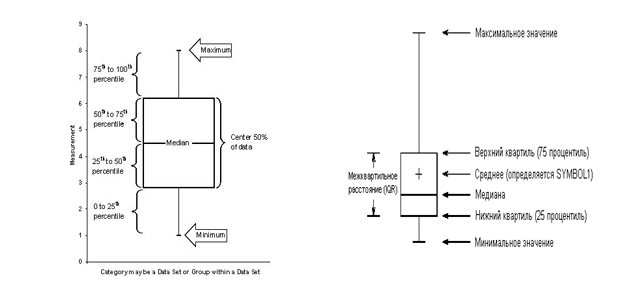
Вариационный ряд разбивают на четыре интервала, получая, соответственно, 25%, 50% и 75% квантили; 25% и 75% квантили называют также нижним (low quartile) и верхним квартилями(high quartile). 50% квантиль – это медиана. Внутри интерквартильного интервала (между 25% и 75% квантилями) лежат 50% наиболее типичных (близких к центральному) значений.
Таким образом, в случае нормального распределения вариационный ряд описывается средней величиной и стандартным отклонением, если распределение неизвестно или оно отлично от нормального, центральную тенденцию и разброс можно описать с помощью медианы, нижнего и верхнего квартиля (интерквартильным интервалом).
Рис.4 Графическое представление описательной статистики (коробчатый график, «коробка с усами», box-plot)
Проверка нормальности распределения
Соответствие экспериментального распределения нормальному проверяется следующими способами:
х ± 0.3 s находится 25 % всех единиц наблюдения;
х ± 0.7 s находится 50 % всех единиц наблюдения;
х ± l,l s находится 75 % всех единиц наблюдения;
х ± 3,0 s находится 99 % всех единиц наблюдения.
— при нормальном распределении, которое обладает симметричностью:
— правило «двух третей» Юла:
а). если распределение симметрично: Me = Mo;
б). если распределение обладает правосторонней асимметрией: Me > Mo;
в). если распределение имеет левостороннюю асимметрией Me 0
в) при левосторонней асимметрии: A s s × f, то «выскакивающая» варианта исключается из исследования;
Средние величины и показатели вариации
Средние величины и общие принципы их вычисления
Средние величины относятся к обобщающим статистическим показателям, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на основе большого количества индивидуальных значений варьирующего признака. Для выяснения сущности средней величины необходимо рассмотреть особенности формирования значений признаков тех явлений, по данным которых исчисляют среднюю величину.
Известно, что единицы каждого массового явления обладают многочисленными признаками. Какой бы из этих признаков мы ни взяли, его значения у отдельных единиц будут различными, они изменяются, или, как говорят в статистике, варьируют от одной единицы к другой. Так, например, заработная плата работника определяется его квалификацией, характером труда, стажем работы и целым рядом других факторов, поэтому изменяется в весьма широких пределах. Совокупное влияние всех факторов определяет размер заработка каждого работника, тем не менее можно говорить о среднемесячной заработной плате работников разных отраслей экономики. Здесь мы оперируем типичным, характерным значением варьирующего признака, отнесенным к единице многочисленной совокупности.
Средняя величина отражает то общее, что характерно для всех единиц изучаемой совокупности. В то же время она уравновешивает влияние всех факторов, действующих на величину признака отдельных единиц совокупности, как бы взаимно погашая их. Уровень (или размер) любого общественного явления обусловлен действием двух групп факторов. Одни из них являются общими и главными, постоянно действующими, тесно связанными с природой изучаемого явления или процесса, и формируют то типичное для всех единиц изучаемой совокупности, которое и отражается в средней величине. Другие являются индивидуальными, их действие выражено слабее и носит эпизодический, случайный характер. Они действуют в обратном направлении, обусловливают различия между количественными признаками отдельных единиц совокупности, стремясь изменить постоянную величину изучаемых признаков. Действие индивидуальных признаков погашается в средней величине. В совокупном влиянии типичных и индивидуальных факторов, которое уравновешивается и взаимно погашается в обобщающих характеристиках, проявляется в общем виде известный из математической статистики фундаментальный закон больших чисел.
В совокупности индивидуальные значения признаков сливаются в общую массу и как бы растворяются. Отсюда и средняя величина выступает как «обезличенная», которая может отклоняться от индивидуальных значений признаков, не совпадая количественно ни с одним из них. Средняя величина отражает общее, характерное и типичное для всей совокупности благодаря взаимопогашению в ней случайных, нетипичных различий между признаками отдельных ее единиц, так как ее величина определяется как бы общей равнодействующей из всех причин.
Однако для того, чтобы средняя величина отражала наиболее типичное значение признака, она должна определяться не для любых совокупностей, а только для совокупностей, состоящих из качественно однородных единиц. Это требование является основным условием научно обоснованного применения средних величин и предполагает тесную связь метода средних величин и метода группировок в анализе социально-экономических явлений. Следовательно, средняя величина – это обобщающий показатель, характеризующий типичный уровень варьирующего признака в расчете на единицу однородной совокупности в конкретных условиях места и времени.
Определяя, таким образом, сущность средних величин, необходимо подчеркнуть, что правильное исчисление любой средней величины предполагает выполнение следующих требований:
Определяющий показатель может выступать в виде суммы значений осредняемого признака, суммы его обратных значений, произведения его значений и т. п. Связь между определяющим показателем и средней величиной выражается в следующем: если все значения осредняемого признака заменить средним значением, то их сумма или произведение в этом случае не изменит определяющего показателя. На основе этой связи определяющего показателя со средней величиной строят исходное количественное отношение для непосредственного расчета средней величины. Способность средних величин сохранять свойства статистических совокупностей называют определяющим свойством.
Средняя величина, рассчитанная в целом по совокупности, называется общей средней; средние величины, рассчитанные для каждой группы, – групповыми средними. Общая средняя отражает общие черты изучаемого явления, групповая средняя дает характеристику явления, складывающуюся в конкретных условиях данной группы.
Способы расчета могут быть разные, поэтому в статистике различают несколько видов средней величины, основными из которых являются средняя арифметическая, средняя гармоническая и средняя геометрическая.
В экономическом анализе использование средних величин является основным инструментом для оценки результатов научно-технического прогресса, социальных мероприятий, поиска резервов развития экономики. В то же время следует помнить о том, что чрезмерное увлечение средними показателями может привести к необъективным выводам при проведении экономико-статистического анализа. Это связано с тем, что средние величины, будучи обобщающими показателями, погашают, игнорируют те различия в количественных признаках отдельных единиц совокупности, которые реально существуют и могут представлять самостоятельный интерес.
Виды средних величин
В статистике используют различные виды средних величин, которые делятся на два больших класса:
Для вычисления степенных средних необходимо использовать все имеющиеся значения признака. Мода и медиана определяются лишь структурой распределения, поэтому их называют структурными, позиционными средними. Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней степенной невозможен или нецелесообразен.
Самый распространенный вид средней величины – средняя арифметическая. Под средней арифметической понимается такое значение признака, которое имела бы каждая единица совокупности, если бы общий итог всех значений признака был распределен равномерно между всеми единицами совокупности. Вычисление данной величины сводится к суммированию всех значений варьирующего признака и делению полученной суммы на общее количество единиц совокупности. Например, пять рабочих выполняли заказ на изготовление деталей, при этом первый изготовил 5 деталей, второй – 7, третий – 4, четвертый – 10, пятый– 12. Поскольку в исходных данных значение каждого варианта встречалось только один раз, для определения средней выработки одного рабочего следует применить формулу простой средней арифметической:
т. е. в нашем примере средняя выработка одного рабочего равна
Наряду с простой средней арифметической изучают среднюю арифметическую взвешенную. Например, рассчитаем средний возраст студентов в группе из 20 человек, возраст которых варьируется от 18 до 22 лет, где xi – варианты осредняемого признака, fi – частота, которая показывает, сколько раз встречается i-е значение в совокупности (табл. 5.1).
Средний возраст студентов
Применяя формулу средней арифметической взвешенной, получаем:
Для выбора средней арифметической взвешенной существует определенное правило: если имеется ряд данных по двум показателям, для одного из которых надо вычислить
среднюю величину, и при этом известны численные значения знаменателя ее логической формулы, а значения числителя неизвестны, но могут быть найдены как произведение этих показателей, то средняя величина должна высчитывать-ся по формуле средней арифметической взвешенной.
В некоторых случаях характер исходных статистических данных таков, что расчет средней арифметической теряет смысл и единственным обобщающим показателем может служить только другой вид средней величины – средняя гармоническая. В настоящее время вычислительные свойства средней арифметической потеряли свою актуальность при расчете обобщающих статистических показателей в связи с повсеместным внедрением электронно-вычислительной техники. Большое практическое значение приобрела средняя гармоническая величина, которая тоже бывает простой и взвешенной. Если известны численные значения числителя логической формулы, а значения знаменателя неизвестны, но могут быть найдены как частное деление одного показателя на другой, то средняя величина вычисляется по формуле средней гармонической взвешенной.
Например, пусть известно, что автомобиль прошел первые 210 км со скоростью 70 км/ч, а оставшиеся 150 км со скоростью 75 км/ч. Определить среднюю скорость автомобиля на протяжении всего пути в 360 км, используя формулу средней арифметической, нельзя. Так как вариантами являются скорости на отдельных участках xj = 70 км/ч и Х2 = 75 км/ч, а весами (fi) считаются соответствующие отрезки пути, то произведения вариантов на веса не будут иметь ни физического, ни экономического смысла. В данном случае смысл приобретают частные от деления отрезков пути на соответствующие скорости (варианты xi), т. е. затраты времени на прохождение отдельных участков пути (fi/xi). Если отрезки пути обозначить через fi, то весь путь выразиться как Σfi, а время, затраченное на весь путь, – как Σ fi/xi , Тогда средняя скорость может быть найдена как частное от деления всего пути на общие затраты времени:
В нашем примере получим:
Если при использовании средней гармонической веса всех вариантов (f) равны, то вместо взвешенной можно использовать простую (невзвешенную) среднюю гармоническую:
где xi – отдельные варианты; n – число вариантов осредняемого признака. В примере со скоростью простую среднюю гармоническую можно было бы применить, если бы были равны отрезки пути, пройденные с разной скоростью.
Любая средняя величина должна вычисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялась величина некоторого итогового, обобщающего показателя, который связан с осредняемым показателем. Так, при замене фактических скоростей на отдельных отрезках пути их средней величиной (средней скоростью) не должно измениться общее расстояние.
Форма (формула) средней величины определяется характером (механизмом) взаимосвязи этого итогового показателя с осредняемым, поэтому итоговый показатель, величина которого не должна изменяться при замене вариантов их средней величиной, называется определяющим показателем. Для вывода формулы средней нужно составить и решить уравнение, используя взаимосвязь осредняемого показателя с определяющим. Это уравнение строится путем замены вариантов осредняемого признака (показателя) их средней величиной.
Кроме средней арифметической и средней гармонической в статистике используются и другие виды (формы) средней величины. Все они являются частными случаями степенной средней. Если рассчитывать все виды степенных средних величин для одних и тех же данных, то значения
их окажутся одинаковыми, здесь действует правило мажо-рантности средних. С увеличением показателя степени средних увеличивается и сама средняя величина. Наиболее часто применяемые в практических исследованиях формулы вычисления различных видов степенных средних величин представлены в табл. 5.2.
Виды степенных средних
Средняя геометрическая применяется, когда имеется n коэффициентов роста, при этом индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики. Средняя характеризует, таким образом, средний коэффициент роста. Средняя геометрическая простая рассчитывается по формуле
Формула средней геометрической взвешенной имеет следующий вид:
Приведенные формулы идентичны, но одна применяется при текущих коэффициентах или темпах роста, а вторая – при абсолютных значениях уровней ряда.
Средняя квадратическая применяется при расчете с величинами квадратных функций, используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения и вычисляется по формуле
Средняя квадратическая взвешенная рассчитывается по другой формуле:
Средняя кубическая применяется при расчете с величинами кубических функций и вычисляется по формуле
средняя кубическая взвешенная:
Все рассмотренные выше средние величины могут быть представлены в виде общей формулы:
где – средняя величина; – индивидуальное значение; n – число единиц изучаемой совокупности; k – показатель степени, определяющий вид средней.
При использовании одних и тех же исходных данных, чем больше k в общей формуле степенной средней, тем больше средняя величина. Из этого следует, что между величинами степенных средних существует закономерное соотношение:
Средние величины, описанные выше, дают обобщенное представление об изучаемой совокупности и с этой точки зрения их теоретическое, прикладное и познавательное значение бесспорно. Но бывает, что величина средней не совпадает ни с одним из реально существующих вариантов, поэтому кроме рассмотренных средних в статистическом анализе целесообразно использовать величины конкретных вариантов, занимающие в упорядоченном (ранжированном) ряду значений признака вполне определенное положение. Среди таких величин наиболее употребительными являются структурные, или описательные, средние – мода (Мо) и медиана (Ме).
Мода – величина признака, которая чаще всего встречается в данной совокупности. Применительно к вариационному ряду модой является наиболее часто встречающееся значение ранжированного ряда, т. е. вариант, обладающий наибольшей частотой. Мода может применяться при определении магазинов, которые чаще посещаются, наиболее распространенной цены на какой-либо товар. Она показывает размер признака, свойственный значительной части совокупности, и определяется по формуле
где х0 – нижняя граница интервала; h – величина интервала; fm – частота интервала; fm_1 – частота предшествующего интервала; fm+1 – частота следующего интервала.
Медианой называется вариант, расположенный в центре ранжированного ряда. Медиана делит ряд на две равные части таким образом, что по обе стороны от нее находится одинаковое количество единиц совокупности. При этом у одной половины единиц совокупности значение варьирующего признака меньше медианы, у другой – больше ее. Медиана используется при изучении элемента, значение которого больше или равно или одновременно меньше или равно половине элементов ряда распределения. Медиана дает общее представление о том, где сосредоточены значения признака, иными словами, где находится их центр.
Описательный характер медианы проявляется в том, что она характеризует количественную границу значений варьирующего признака, которыми обладает половина единиц совокупности. Задача нахождения медианы для дискретного вариационного ряда решается просто. Если всем единицам ряда придать порядковые номера, то порядковый номер медианного варианта определяется как (п +1) / 2 с нечетным числом членов п. Если же количество членов ряда является четным числом, то медианой будет являться среднее значение двух вариантов, имеющих порядковые номера n / 2 и n / 2 + 1.
При определении медианы в интервальных вариационных рядах сначала определяется интервал, в котором она находится (медианный интервал). Этот интервал характерен тем, что его накопленная сумма частот равна или превышает полусумму всех частот ряда. Расчет медианы интервального вариационного ряда производится по формуле
где X0 – нижняя граница интервала; h – величина интервала; fm – частота интервала; f– число членов ряда;
∫m-1 – сумма накопленных членов ряда, предшествующих данному.
Наряду с медианой для более полной характеристики структуры изучаемой совокупности применяют и другие значения вариантов, занимающих в ранжированном ряду вполне определенное положение. К ним относятся квартили и децили. Квартили делят ряд по сумме частот на 4 равные части, а децили – на 10 равных частей. Квартилей насчитывается три, а децилей – девять.
Медиана и мода в отличие от средней арифметической не погашают индивидуальных различий в значениях варьирующего признака и поэтому являются дополнительными и очень важными характеристиками статистической совокупности. На практике они часто используются вместо средней либо наряду с ней. Особенно целесообразно вычислять медиану и моду в тех случаях, когда изучаемая совокупность содержит некоторое количество единиц с очень большим или очень малым значением варьирующего признака. Эти, не очень характерные для совокупности значения вариантов, влияя на величину средней арифметической, не влияют на значения медианы и моды, что делает последние очень ценными для экономико-статистического анализа показателями.
Показатели вариации
Целью статистического исследования является выявление основных свойств и закономерностей изучаемой статистической совокупности. В процессе сводной обработки данных статистического наблюдения строят ряды распределения. Различают два типа рядов распределения – атрибутивные и вариационные, в зависимости от того, является ли признак, взятый за основу группировки, качественным или количественным.
Вариационными называют ряды распределения, построенные по количественному признаку. Значения количественных признаков у отдельных единиц совокупности не постоянны, более или менее различаются между собой. Такое различие в величине признака носит название вариации. Отдельные числовые значения признака, встречающиеся в изучаемой совокупности, называют вариантами значений. Наличие вариации у отдельных единиц совокупности обусловлено влиянием большого числа факторов на формирование уровня признака. Изучение характера и степени вариации признаков у отдельных единиц совокупности является важнейшим вопросом всякого статистического исследования. Для описания меры изменчивости признаков используют показатели вариации.
Другой важной задачей статистического исследования является определение роли отдельных факторов или их групп в вариации тех или иных признаков совокупности. Для решения такой задачи в статистике применяются специальные методы исследования вариации, основанные на использовании системы показателей, с помощью которых измеряется вариация. В практике исследователь сталкивается с достаточно большим количеством вариантов значений признака, что не дает представления о распределении единиц по величине признака в совокупности. Для этого проводят расположение всех вариантов значений признака в возрастающем или убывающем порядке. Этот процесс называют ранжированием ряда. Ранжированный ряд сразу дает общее представление о значениях, которые принимает признак в совокупности.
Недостаточность средней величины для исчерпывающей характеристики совокупности заставляет дополнять средние величины показателями, позволяющими оценить типичность этих средних путем измерения колеблемости (вариации) изучаемого признака. Использование этих показателей вариации дает возможность сделать статистический анализ более полным и содержательным и тем самым глубже понять сущность изучаемых общественных явлений.
Самыми простыми признаками вариации являются минимум и максимум – это наименьшее и наибольшее значение признака в совокупности. Число повторений отдельных вариантов значений признаков называют частотой повторения. Обозначим частоту повторения значения признака fi, сумма частот, равная объему изучаемой совокупности будет:
где k – число вариантов значений признака. Частоты удобно заменять частостями – wi. Частость – относительный показатель частоты – может быть выражен в долях единицы или процентах и позволяет сопоставлять вариационные ряды с различным числом наблюдений. Формально имеем:
Для измерения вариации признака применяются различные абсолютные и относительные показатели. К абсолютным показателям вариации относятся среднее линейное отклонение, размах вариации, дисперсия, среднее квадратическое отклонение.
Размах вариации (R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности: R = Xmax – Xmin. Этот показатель дает лишь самое общее представление о колеблемости изучаемого признака, так как показывает разницу только между предельными значениями вариантов. Он совершенно не связан с частотами в вариационном ряду, т. е. с характером распределения, а его зависимость может придавать ему неустойчивый, случайный характер только от крайних значений признака. Размах вариации не дает никакой информации об особенностях исследуемых совокупностей и не позволяет оценить степень типичности полученных средних величин. Область применения этого показателя ограничена достаточно однородными совокупностями, точнее, характеризует вариацию признака показатель, основанный на учете изменчивости всех значений признака.
Для характеристики вариации признака нужно обобщить отклонения всех значений от какой-либо типичной для изучаемой совокупности величины. Такие показатели
вариации, как среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, основаны на рассмотрении отклонений значений признака отдельных единиц совокупности от средней арифметической.
Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их средней арифметической:
– абсолютное значение (модуль) отклонения варианта от средней арифметической; f– частота.
Первая формула применяется, если каждый из вариантов встречается в совокупности только один раз, а вторая – в рядах с неравными частотами.
Существует и другой способ усреднения отклонений вариантов от средней арифметической. Этот очень распространенный в статистике способ сводится к расчету квадратов отклонений вариантов от средней величины с их последующим усреднением. При этом мы получаем новый показатель вариации – дисперсию.
Дисперсия (σ 2 ) – средняя из квадратов отклонений вариантов значений признака от их средней величины:
Вторая формула применяется при наличии у вариантов своих весов (или частот вариационного ряда).
В экономико-статистическом анализе вариацию признака принято оценивать чаще всего с помощью среднего квадратического отклонения. Среднее квадратическое отклонение (σ) представляет собой корень квадратный из дисперсии:
Среднее линейное и среднее квадратическое отклонения показывают, на сколько в среднем колеблется величина признака у единиц исследуемой совокупности, и выражаются в тех же единицах измерения, что и варианты.
В статистической практике часто возникает необходимость сравнения вариации различных признаков. Например, большой интерес представляет сравнение вариаций возраста персонала и его квалификации, стажа работы и размера заработной платы и т. д. Для подобных сопоставлений показатели абсолютной колеблемости признаков – среднее линейное и среднее квадртическое отклонение – не пригодны. Нельзя, в самом деле, сравнивать колеблемость стажа работы, выражаемую в годах, с колеблемостью заработной платы, выражаемой в рублях и копейках.
При сравнении изменчивости различных признаков в совокупности удобно применять относительные показатели вариации. Эти показатели вычисляются как отношение абсолютных показателей к средней арифметической (или медиане). Используя в качестве абсолютного показателя вариации размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, получают относительные показатели колеблемости:
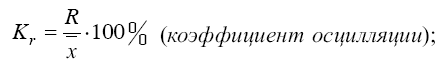
– наиболее часто применяемый показатель относительной колеблемости, характеризующий однородность совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % для распределений, близких к нормальному.