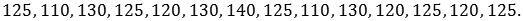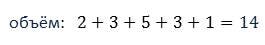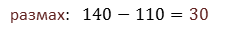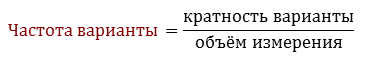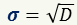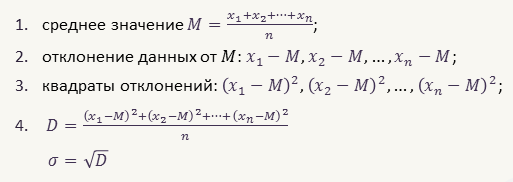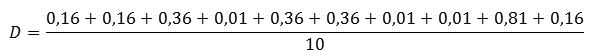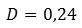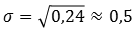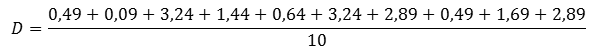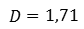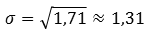Что такое варианта измерения
Разделы: Математика
Цель: рассмотреть статистическую обработку информации, и её основные характеристики.
I. Сообщение темы и цели урока
III. Изучение нового материала
Наш XXI в. характеризуют различным образом: век генной инженерии, век новых технологий ( в частности, нанотехнологий), век астрофизики (проверка основополагающих космогонических теорий, большой андронный коллайдер) и т. д. Если вдуматься, все определения объединяет прежде всего, получение принципиально новой информации. Поэтому правильнее назвать наш век веком информации. Буквально за несколько последних лет появились сверхмощные компьютеры, Интернет, различные поисковые системы, разрабатываются и совершенствуются методики обработки информации и т. п.
Многие из нас участвуют в переписи населения, выборах, опросах и т. д. При этом появляется определённая информация. Задача статистики – отражение этой информации и её обработка. Для этого необходимо ввести некоторые статистические характеристики. Рассмотрим следующий пример.
Пример
В финал конкурса «Мисс факультета» Вышли 10 студенток, за которых болели и голосовали 90 студентов. В таблице приведены результаты голосования за участниц с номерами 1-10.
| № участницы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Число голосов | 7 | 3 | 14 | 15 | 7 | 4 | 3 | 7 | 20 | 10 |
Прежде всего, возникает вопрос о наглядном отражении результатов голосования. Из курса алгебры вы знаете, что графическая информация нагляднее табличной. Поэтому применяют три вида графического отражения информации – диаграммы.
Первый вид диаграммы – линейная диаграмма (или многоугольник распределения) строится как обычный график. По оси абцисс откладываются номера участниц, по оси ординат – число голосов, отданных за данную участницу, т. е. точки (1,7), (2,3), (3,14) и т. д. Для наглядности отмеченные точки соединены отрезками.
Второй вид диаграммы – столбчатая диаграмма (или гистограмма распределения) строится следующим образом. В окрестности каждой отмеченной точки по оси абцисс строят прямоугольник, высота которого равна соответствующей ординате. При этом обычно ширину прямоугольников делают одинаковой. Достаточно часто прямоугольники изображаются таким образом, что два соседних имеют общую сторону. При этом прямоугольники могут штриховаться (см. учебник)
На практике применяют все три вида диаграмм.
Обсудим некоторые характеристики рассматриваемого примера.
Объём измерения – количество источников информации (т.е. число опрошенных или число голосов) в данном случае 90.
Размах измерения – разница между наибольшим и наименьшим значениями результатов измерения. В данном случае 20 – 3 = 17, так как наибольшее число голосов 20, наименьшее 3.
Мода измерения – наиболее часто встречающийся результат. В данном случае 9, так как за участницу №9 было подано 20 голосов (наибольшее количество).
Среднее (или среднее арифметическое) – частное от деления суммы всех результатов измерения на объём измерения. В данном случае получают:
Обычно результатами измерений являются некоторые числа. Каждое число, встретившееся в конкретном измерении, называют вариантой измерения. В конкретном измерении его варианты могут быть никак не связаны (например, билетики с результатами голосования). Однако обычно результаты обрабатываются. Если записать все варианты измерения в некотором порядке (например, по времени поступления голосов в жюри), то получится ряд данных измерения. Обычно упорядочивание проходит определённым образом. Запишем полученные варианты в порядке их возрастания (точнее, неубывания). Получим сгруппированный ряд данных:
Среднюю варианту в сгруппированном ряде данных в случае нечётного количества чисел или средне арифметическое, двух стоящих посередине вариант в случае чётного количества чисел называют медианой измерения. В нашем случае средних варианты две, это варианты 45 и 46. Каждая из них равна 5, значит, и медиана равна
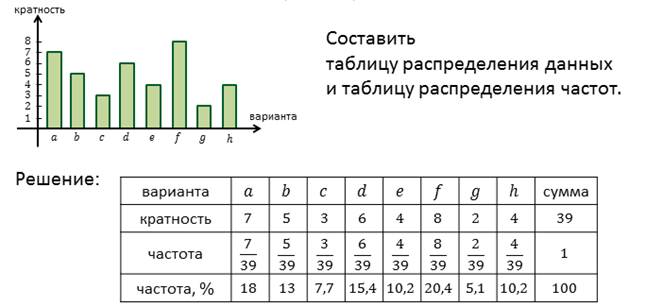
В нашем примере ответ 1 встретился 7 раз (за участницу №1 проголосовали 7 человек). Поэтому говорят, что абсолютная частота (или кратность) варианты 1 равна семи. Поэтому ( в другой терминологии ранее приведённая таблица имеет вид:
| Варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Сумма |
| Кратность | 7 | 3 | 14 | 15 | 7 | 4 | 3 | 7 | 20 | 10 | 90 |
Таким образом, получаем таблицу распределения данных измерения. Графа «Сумма» добавляется для контроля: число в этой графе обязательно равняется объёму измерения.
Заметим, что при вычислении среднего арифметического в неявном виде уже использовалось понятие кратности варианты.
Введём ещё понятие частоты данной варианты – частное от деления кратности варианты на объём измерения. Например для варианты 1 находим частоту 
IV. Задание на уроке (работа в компьютерном классе)
§19 № 1, 3, 5, 8, 10, 12, 17, 19
V. Задание на дом: §19, №2, 9, 14, 18, 20
1. Статистика — дизайн информации
Теория:
Теперь сгруппированные данные необходимо представить в виде таблицы.
2. Составление таблиц распределения данных.
Если разделить кратность вариантов на объём измерения, то получим частоту вариантов.
3. Графическое представление информации.
Распределение данных измерения рационально задавать в табличном виде. Однако нам известно, что и для функций есть табличный способ их задания. Таблицы являются связующим звеном. С их помощью осуществляется переход от распределения данных к функциям и графикам.
График распределения выборки является графическим представлением информации. Согласно табличным сведениям из примеров выше отметим точки, у которых абсциссы — это номер варианта, а ординаты — кратность. Соединяем отрезками полученные точки:
Получили многоугольник или полигон распределения данных. Собственно, polygon и переводится как «многоугольник».
Размах измерения — это разность между максимальной и минимальной вариантами.
Мода измерения — вариант, который в измерении встречался чаще других.
Среднее значение — среднее арифметическое, или просто среднее. Для нахождения среднего значения нужно:
1) вычислить сумму всех данных измерения;
2) полученную сумму разделить на количество данных.
Статистика – получение, обработка, анализ и публикация информации, характеризующей количественные закономерности жизни в обществе в неразрывной связи с их количественным содержанием.
2) получение и хранение информации ;
3)выработка различных прогнозов;
4)оценка достоверности прогнозов и т.д.
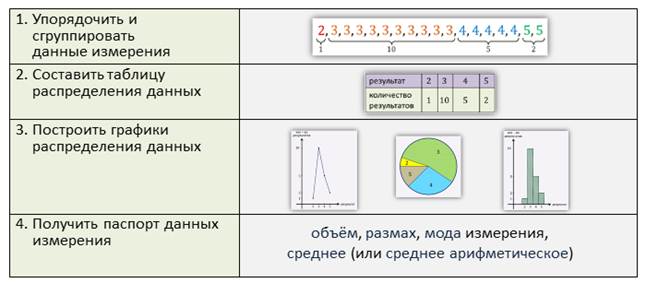
1) Упорядочение и группировка измерений.
2)Составление таблиц распределения данных.
3)Построение графиков распределения данных.
4)Получение «паспорта» данных измерения, в
котором собраны основные числовые
характеристики полученной информации.
У 50 рабочих городского предприятия попросили оценить время,
которое они в среднем тратят на проезд от дома до работы. Получились следующие данные в минутах
(с точностью до 10 минут).
30 40 60 50 100 60 90 10 20 50
60 120 30 40 60 20 60 10 50 60
1)Заявлено ли время менее 10 минут?
2)Заявлено ли время более 180 минут?
Общий ряд данных — это ряд всех значений
измерения, заключённых в промежутке от наименьшего
возможного до наибольшего возможного значений.
Выпишем общий ряд данных в измерениях
1) Месяц рождения учеников нашей школы.
2) Год рождения ваших родственников и знакомых.
3)Годовой процент начислений по вкладам в банке.
4)Начальные буквы в первой строке стихотворения.
1)1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
2)1910, 1911, 1912,…, 2008, 2009, 2010, 2011.
3)0,1; 0,2; 0,3;…;0,9; 1; 2; 3;…;14; 15.
Варианта измерения — это один из
Ряд данных измерения — это
ряд из всех его вариант.
результатов этого измерения.
10, 20, 30, 40, 50,60, 80, 90, 100, 120
30 40 60 50 100 60 90 10 20 50
60 120 30 40 60 20 60 10 50 60
Выпишем ряд данных измерения, состоящего из всех разных букв
первых двух строк стихотворений:
Всё, что ты видел, забудь…
И судьба сосны ясна…
а, б, в, д, е, и, н, о, р, с, т, у, ы, ь, э, я.
Кратностью варианты измерения называется число k , которое показывает сколько раз встретилась варианта среди всех данных конкретного измерения.
2 10 2 3 4 5 3 8 9 4
3 5 2 5 3 3 5 6 6 5
3 4 6 5 10 6 9 1 2 5
9 8 2 4 5 1 5 4 3 4
6 12 3 4 6 2 6 1 5 6
1,1,2,…,2, 3,…,3, 4,…,4, 5,…,5, 6,…,6, 8,8,8, 9, 9, 10, 10, 12
Запишем общий ряд данных
1, 2 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
1,1,2,…,2, 3,…,3, 4,…,4, 5,…,5, 6,…,6, 8,8,8, 9, 9, 10, 10, 12
Урок по математике на тему «Задачи математической статистики» (11 класс)
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Тема урока : Задачи математической статистики.
Обучающая: Научить учащихся решать задачи по обработке
статистических данных, используя понятия:
объём измерения, размах измерения, мода
измерения, среднее арифметическое, медиана
измерения, варианта измерения, кратность
варианты, и составлять данные в виде таблиц,
диаграмм, графиков. Ввести понятия: частота
варианты, частота варианты (в процентах).
Формировать умения учащихся, решать задачи на
обработку статистических данных, используя
данные в виде таблиц, диаграмм, графиков.
Развивать логическое и математическое мышление.
Воспитывать культуру речи, построения плана
ответа, сознательной дисциплины, культуры
конструктивного мышления, активность на уроке,
аккуратность при выполнении записи на доске и в
тетради, положительный интерес к изучаемому
Вид урока: Урок решения задач на обработку статистических
данных, используя данные в виде таблиц,
Методы обучения: Репродуктивный.
— Математика Учебник Общеобразовательные дисциплины
Начальное и среднее профессиональное образование
Москва Издательский центр «Академия» 201
— Математика Учебник Общеобразовательные дисциплины
для профессий и специальностей социально-экономического
профиля. Авторы В.А. Гусев, С.Г.Григорьев, С.В.Иволгина
Москва Издательский центр «Академия» 2011
— Математика Задачник Общеобразовательные дисциплины
Начальное и среднее профессиональное образование
Москва Издательский центр «Академия» 2012
— дидактический раздаточный материал (карточки для
1. Организационный момент урока
2. Целевая ориентация
( Преподаватель формулирует тему, цели и задачи урока. Мотивирует учащихся к учебной деятельности. Разъясняет последовательность этапов урока, приводящих к достижению цели)
3. Проверка домашнего задания.
4. Вопросы для закрепления изученного материала.
1). Перечислить основные этапы простейшей статистической обработки данных.
2). Что называют объемом измерения?
3). Что такое размах измерения?
4). Что называют модой измерения?
5). Что называют средним арифметическим?
6). Что называют вариантой измерения?
7). Что называют медианой измерения?
Формирование навыков умственного труда
Решение задач у доски
В таблице распределения данных часть информации была утеряна. Восстановить ее. Если известно, что объем измерения равен 20, размах измерения равен 6, а мода равна 2.
По определению. В графе «Сумма» должен стоять объём измерения, т.е. 20. Этот объём равен сумме всех кратностей, значит, кратность варианты «0», равна 20 – (5+1+7+3) = 4.
По приведённой гистограмме распределения данных найти: количество вариант измерения, объем, размах. моду измерения, наиболее удалённую от моды варианту и ее кратность. Составить таблицу распределения данных.
Количество вариант – это количество столбиков в гистограмме, т.е. 7. Объем измерения равен сумме кратностей всех вариант, т.е. равен сумме высот всех семи столбиков: 3+2+7+3+5+4+1 = 25. Таблица распределения выглядит так:
1). Наибольшая варианта равна 10, а наименьшая равна 2.
2). Размах равен 8. (10 – 2) =8.
3). Мода измерения равна 5, так как она встречалась чаще других – 7 раз.
4). На наибольшем расстоянии от моды находится варианта 10, её кратность равна 1.
Определение: Если кратность варианты разделить на объем измерения, то получится частота варианты. Это число показывает, какую часть (долю) среди всех данных составляют данные, равные выбранной варианте.
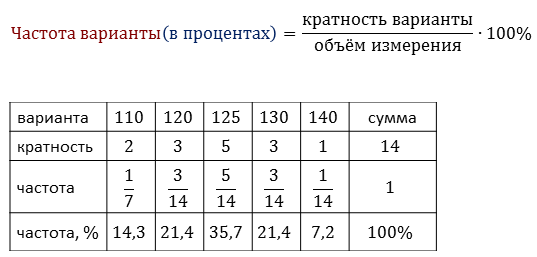
Частоту варианты можно измерить и в процентах.
Частота варианты (в процентах) =
В десятых классах трёх школ микрорайона провели проверочный диктант по русскому языку. По их результатам изображена гистограмма распределения полученных отметок.
а) Найти: общее количество работ, частоту пятёрок, процентную частоту
б) Заполнить сводную таблицу распределения данных.
в) Построить гистограмму распределения частот ( в процентах).
г) Построить круговую диаграмму распределения частот (в процентах).
а) На гистограмме указано, что двоек было 40, троек – 50, четвёрок – 75, пятёрок – 35. значит. Всего было 200 работ. Это есть объём измерения. Частота пятёрок равна 
б) Так как все кратности известны, то можно заполнить всю таблицу распределения:
в) Для построения гистограммы распределения частот (в процентах) используем первую и четвёртую строки. Получим четыре вертикальных столбика. Основания которых соответствуют полученным отметкам, а высоты равны найденным частотам ( в процентах).
5. Вопросы для закрепления изученного материала.
1). Что называют частотой варианты?
2). По какой формуле измеряют частоту варианты в процентах?
6. Итог урока. Домашнее задание.
По приведённой гистограмме распределения данных найти:
а) количество вариант и объем измерения;
б) размах и моду измерения;
в) таблицу распределения данных;
г) среднее результатов измерения.
1) Количество вариант – это количество столбиков в гистограмме, т.е. 9. Объем измерения равен сумме кратностей всех вариант, т.е. равен сумме высот всех девяти столбиков: 5+6+3+7+4+11+5+4+5 = 50. Таблица распределения выглядит так:
2). Наибольшая варианта равна 10, а наименьшая равна 2.
Размах равен 8. (10 – 2) = 8.
Мода измерения равна 7, так как она встречалась чаще других – 11 раз.
3). Таблица распределения выглядит так:
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: 281626
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
ВПР для школьников в 2022 году пройдут весной
Время чтения: 1 минута
Учителям истории предлагают предоставить право бесплатно посещать музеи
Время чтения: 2 минуты
В России планируют создавать пространства для подростков
Время чтения: 2 минуты
Госдума приняла закон об использовании онлайн-ресурсов в школах
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Статистическая обработка данных
Урок 23. Алгебра 11 класc
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Статистическая обработка данных»
• рассмотреть основные этапы статистической обработки данных;
• познакомиться с понятием «дисперсия»;
• рассмотреть примеры вычисления дисперсии с помощью специального алгоритма.
Слово статистика происходит от латинского «статус», означающего «состояние дел».
Этому понятию можно дать следующее определение.
Статистика – отрасль знаний, в которой излагаются общие вопросы сбора, измерения и анализа массовых статистических (количественных или качественных) данных; изучение количественной стороны массовых общественных явлений в числовой форме.
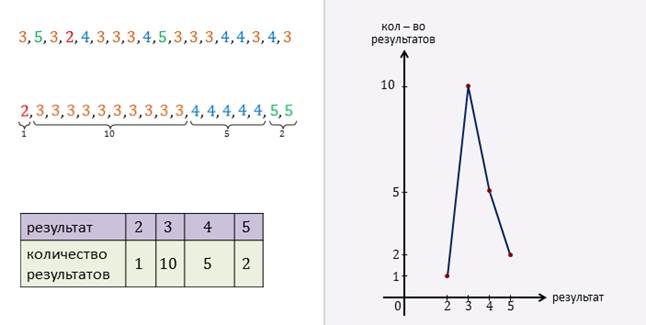
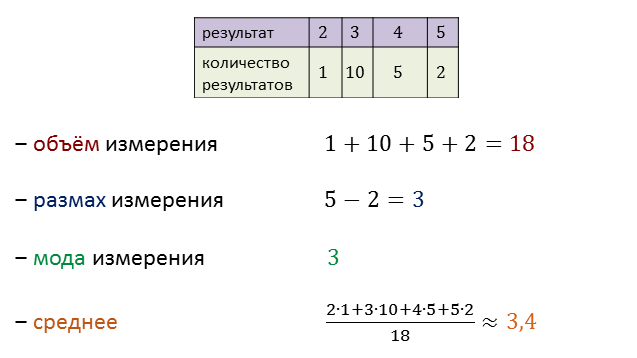
Анализируя результаты написания контрольной работы по математике, учитель сгруппировал все данные таким образом.
Только 1 человек получил двойку. Десять получили тройку. Пятеро человек написали контрольную на 4. И только двое получили пятёрки.
Всю эту информацию можно собрать в одной таблице.
Также эти данные можно представить графически.
На горизонтальной оси отметим все возможные результаты, а на вертикальной — их количество.
Так точки 2 1, 3 10, 4 5 и 5 2 будут соответствовать парам значений из таблицы. Соединим их ломаной. Так мы с вами получили многоугольник распределений.
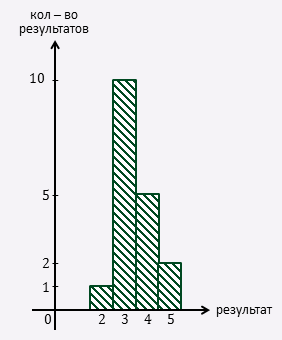
А теперь для каждой пары значений изобразим соответствующий столбец и раздуем его до ширины равной одному. Получаем столбчатую диаграмму — гистограмму распределений.
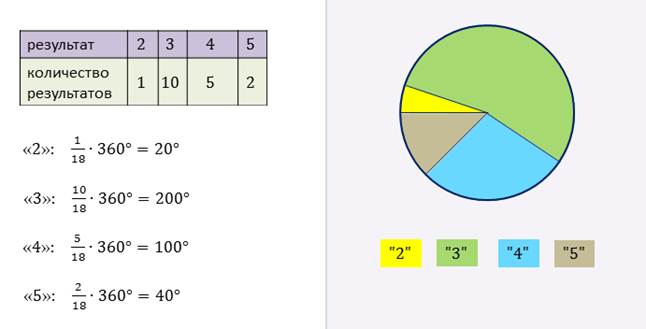
Рассмотрим ещё один способ.
Представим все данные в виде круга.
Так получается круговая диаграмма.
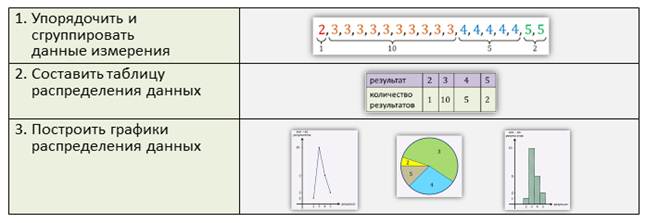
Сейчас мы с вами на конкретном примере разобрали основные этапы статистической обработки данных.
К этим трём этапам обычно добавляют ещё один: получение паспорта данных измерений, состоящий из нескольких числовых характеристик.
К этим характеристикам относят объём, размах, моду и среднее измерение.
Объём измерения в данном случае равен 18, так как обрабатывались результаты восемнадцати учеников.
Размах измерения равен 9. Это разница между наибольшим и наименьшим результатами.
Мода измерения — это самый популярный, «модный» результат. В данном случае она равна 3.
Среднее (или среднее арифметическое). Это частное суммы всех результатов измерений на объём измерений.
Чаще всего, как вы понимаете, результатами измерений являются числа. Каждое число, встретившееся в конкретном измерении, называют вариантой измерения.
Если записать все варианты измерений, то получится ряд данных измерения.
Если записать их в порядке возрастания, то получим сгруппированный ряд данных.
Среднюю варианту называют медианой измерения. Если их две, то медиана равна их среднему арифметическому.
В нашем примере средними вариантами являются варианты под номерами 9 и 10. Они обе равны 3, значит, и медиана равна 3.
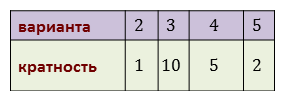
Каждая варианта встречается некоторое число раз, его называют кратностью данной варианты.
Для нашего примера таблица распределения данных примет такой вид.
Применим полученные знания при решении задачи.
На уроке физкультуры 14 школьников прыгали в высоту, а учитель записывал их результаты. Получился такой ряд данных
Требуется сгруппировать данные, составить таблицу их распределения, а также найти объём, размах, моду, среднее и медиану измерения.
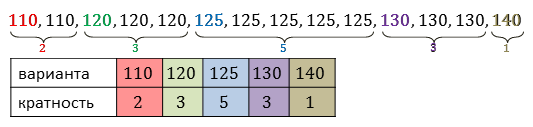
Для начала сгруппируем данные, расположив их в порядке возрастания.
Это позволит нам составить таблицу распределения данных.
Теперь найдём объём измерения.
Размах измерения равен разности наибольшей и наименьшей вариант.
Среднее значение равно частному суммы всех полученных значений и объёма измерения.
Мода измерения равна 125. Ведь это самый популярный результат.
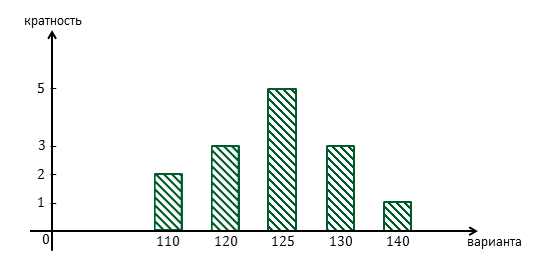
А теперь, по полученной таблице распределения данных построим многоугольник распределения и гистограмму распределения.
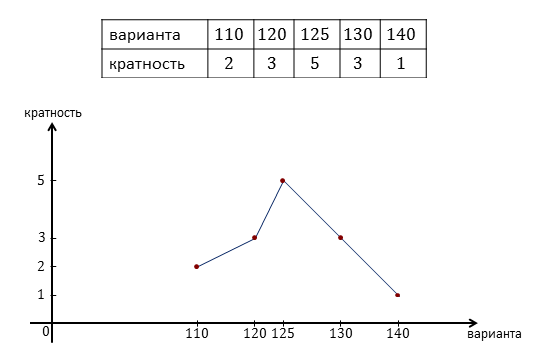
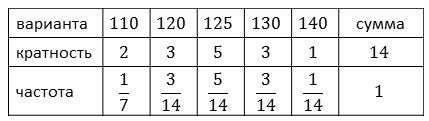
Мы имеем 5 вариант: 110, 120, 125, 130 и 140.
Кратность первой варианты равна 2, второй — 3, третьей — 5, четвёртой — 3, и пятой —1.
Соединив полученные точки, получим многоугольник распределения данных.
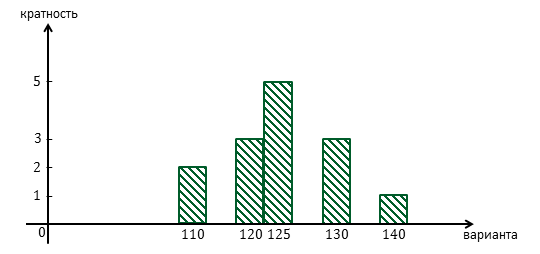
Тогда гистограмма примет такой вид.
Обратите внимание, варианты могут располагаться неравномерно на оси Ox, между ними могут быть пропуски.
Например, значение 115 не встретилось ни разу, то есть её кратность равна 0. Очевидно, что такое значение не может быть вариантой.
Для построение гистограммы можно было использовать номинативную шкалу, то есть по горизонтали распределить номинации, варианты, а на вертикальной оси оставить значения их кратностей. Гистограмма примет такой вид.
В этом случае вариантами могут быть не только числа.
Если кратность варианты разделить на объём измерения, то получится частота варианты.
Найдём частоту каждой варианты данной задачи. Обратите внимание, сумма частот всегда равна единице.
Частоту также можно выразить в процентах. Сумма частот в процентах, очевидно, всегда равна 100.
Только что с помощью таблицы распределения данных мы составили таблицу распределения частот.
А теперь рассмотрим такой случай.
Числовую характеристику данных измерения, отвечающую за разброс данных вокруг среднего значения, называют дисперсией D.
Средним квадратическим отклонением называют:
Чем меньше эти значения, тем плотнее группируются данные измерения вокруг среднего значения.
Существует алгоритм вычисления дисперсии данных.
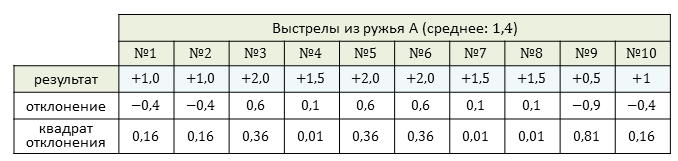
Воспользуемся этим алгоритмом и найдём значение дисперсии результатов отклонения для каждого ружья.
Проведём подсчёты для ружья А. Их удобно производить в таблице.
Найдём их среднее значение. Получаем, что дисперсия равна:
А среднее квадратическое отклонение равно:
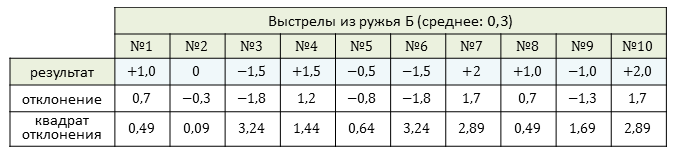
Вычислим значение дисперсии для ружья Б.
Можем вычислить дисперсию как среднее квадратов отклонений.
Тогда среднее квадратическое отклонение равно:
Видим, что дисперсии отличаются практически в 7 раз, а средние квадратические отклонения примерно в 3 раза.
Можно сказать, что ружьё Б стреляет с разбросом в 3 раза большим, чем ружьё А. Поэтому ружьё А точнее.
Подведём итоги нашего урока.
Сегодня вы познакомились и рассмотрели на примерах этапы статистической обработки данных.
Каждое значение, полученное в ходе измерений, мы договорились называть вариантой. А число повторений данной варианты, называют её кратностью.
Вы познакомились с формулой отыскания частоты варианты. И научились составлять таблицу распределения частот.
Также узнали, что числовую характеристику данных измерения, отвечающую за разброс данных вокруг среднего значения, называют дисперсией.
А ещё, рассмотрели примеры нахождения этих величин с помощью специального алгоритма.