Что такое вариант в статистике
Понятие вариации в статистике
Правила построения рядов распределения
Ряды распределения представляют собой простейшую группировку, в которой каждая выделенная группа характеризуется одним показателем.
В зависимости от признака, положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения.
Атрибутивными называют ряды распределения, построенные по качественным признакам, то есть признакам, не имеющим числового выражения.
Атрибутивные ряды распределения характеризуют состав совокупности по тем или иным существенным признакам. Взятые за несколько периодов, эти данные позволяют исследовать изменение структуры.
Вариационными рядами называют ряды распределения, построенные по количественному признаку. Любой вариационный ряд состоит из двух элементов: вариантов и частот. Вариантами называются отдельные значения признака, которые он принимает в вариационном ряду, то есть конкретное значение варьирующего признака. Частотами называются численности отдельных вариант или каждой группы вариационного ряда, то есть это числа, которые показывают, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот определяет численность всей совокупности, ее объем. Частностями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частностей равна 1 или 100%.
Правила построения рядов распределения аналогичны правилам построения группировки.
Группировки, построенные за один и тот же период времени, но для разных объектов или, наоборот, для одного объекта, но за два разных периода времени могут оказаться несопоставимыми из-за различного числа выделенных групп или неодинаковости границ интервалов.
Вторичная группировка, или перегруппировка сгруппированных данных применяется для лучшей характеристики изучаемого явления (в случае, когда первоначальная группировка не позволяет четко выявить характер распределения единиц совокупности), либо для приведения к сопоставимому виду группировок с целью проведения сравнительного анализа.
Термин «вариация» произошел от латинского varito —изменение, колеблемость, различие. Однако не всякое различие называется вариацией. Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов.
Исследование вариации в статистике имеет важное значение, т.к. дает возможность оценить степень воздействия на данный признак других варьирующих признаков. Определение вариации необходимо при организации выборочного наблюдения, построения статистических моделей, разработке материалов экспертных опросов и т.д.
Средняя величина — это обобщающая характеристика признака изучаемой совокупности. Она не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней. Поэтому для характеристики колеблемости признака используют показатели вариации.
Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае.
Колебания отдельных значений характеризуют показатели вариации.
Термин «вариация» произошел от лат. variatio – «изменение, колеблемость, различие». Под вариацией понимают количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую.
Систематическая вариация помогает оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов.
Для характеристики колеблемости признака используется ряд показателей, такие как размах вариации, определяемый как разность между наибольшим (Хмах) и наименьшим(xmjn) значениями вариантов:
Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней без учета знака этих отклонений.
Меру вариации более объективно отражает показатель дисперсии.
Среднее квадратическое отклонение – это мерило надежности средней.
Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах, которые позволяют сравнивать характер рассеивания в различных распределениях. Расчет показателей меры относительного рассеивания осуществляют отношением абсолютного показателя рассеивания к средней арифметической и умножают на 100%.
При помощи группировок, подразделив изучаемую совокупность на группы, однородные по признаку-фактору, можно определить три показателя колеблемости признака в совокупности: общую дисперсию, межгрупповую дисперсию и среднюю из внутригруп-повых дисперсий.
Общая дисперсия характеризует вариацию признака, зависящую от всех условий в изучаемой статистической совокупности.
Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием признака-фактора, положенного в основу группировки, характеризует колеблемость групповых (частных) средних хi и общей средней хо.
Средняя внутригрупповых дисперсий характеризует случайную вариацию в каждой отдельной группе, возникает под влиянием факторов кроме положенного в основу группировки.
Дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, и доли единиц, не обладающих им.
22. Показатели вариации: абсолютные и относительные
Вариация – различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.
К показателям вариации относятся:
I группа — абсолютные показатели вариации
II группа — относительные показатели вариации
· Для измерения вариации в статистике применяют несколько способов.
· Наиболее простым является расчет показателя размаха вариации Н как разницы между максимальным (Xmax ) и минимальным (Xmin) наблюдаемыми значениями признака:
· Однако размах вариации показывает лишь крайние значения признака. Повторяемость промежуточных значений здесь не учитывается.
· Более строгими характеристиками являются показатели колеблемости относительно среднего уровня признака. Простейший показатель такого типа – среднее линейное отклонение Л как среднее арифметическое значение абсолютных отклонений признака от его среднего уровня:
· 
· При повторяемости отдельных значений Х используют формулу средней арифметической взвешенной:
· 
· (Напомним, что алгебраическая сумма отклонений от среднего уровня равна нулю.)
· Показатель среднего линейного отклонения нашел широкое применение на практике. С его помощью анализируются, например, состав работающих, ритмичность производства, равномерность поставок материалов, разрабатываются системы материального стимулирования. Но, к сожалению, этот показатель усложняет расчеты вероятностного типа, затрудняет применение методов математической статистики. Поэтому в статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии.
· Дисперсия признака (s 2 ) определяется на основе квадратической степенной средней:
· 
.
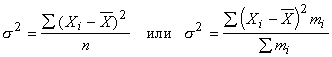
· Показатель s, равный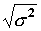 
, называется средним квадратическим отклонением.
· В общей теории статистики показатель дисперсии является оценкой одноименного показателя теории вероятностей и (как сумма квадратов отклонений) оценкой дисперсии в математической статистике, что позволяет использовать положения этих теоретических дисциплин для анализа социально-экономических процессов.
· Если из генеральной совокупности сделать несколько выборок и каждый раз при этом определять среднее значение признака, то возникает задача оценки колеблемости средних. Оценить дисперсию среднего значения можно и на основе всего одного выборочного наблюдения по формуле
· 
,
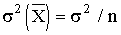
· где n – объем выборки; s 2 – дисперсия признака, рассчитанная по данным выборки.
· Величина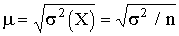 
носит название средней ошибки выборки и является характеристикой отклонения выборочного среднего значения признака Х от его истинной средней величины. Показатель средней ошибки используется при оценке достоверности результатов выборочного наблюдения.
· Показатели относительного рассеивания. Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.
· 1. Коэффициентом осцилляции отражает относительную колеблемость крайних значений признака вокруг средней
· 
.
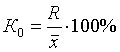
· 2. Относительное линейное отключение характеризует долю усредненного значения признака абсолютных отклонений от средней величины
· 
.
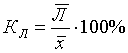
· 3. Коэффициент вариации:
· 
· является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин.
· В статистике совокупности, имеющие коэффициент вариации больше 30–35 %, принято считать неоднородными.
· У такого способа оценки вариации есть и существенный недостаток. Действительно, пусть, например, исходная совокупность рабочих, имеющих средний стаж 15 лет, со средним квадратическим отклонением s = 10 лет, «состарилась» еще на 15 лет. Теперь 
= 30 лет, а среднеквадратическое отклонение по-прежнему равно 10. Совокупность, ранее бывшая неоднородной (10/15 × 100= 66,7%), со временем оказывается, таким образом, вполне однородной (10/30 × 100 = 33,3 %).
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Вариация (статистика)
Вариа́ция — различие значений какого-либо признака у разных единиц совокупности за один и тот же промежуток времени. Причиной возникновения вариации являются различные условия существования разных единиц совокупности. Вариация — необходимое условие существования и развития массовых явлений. [1] Определение вариации необходимо при организации выборочного наблюдения, статистическом моделировании и планировании экспертных опросов. По степени вариации можно судить об однородности совокупности, устойчивости значений признака, типичности средней, о взаимосвязи между какими-либо признаками. [2]
Содержание
Показатели вариации
Абсолютные показатели
где 
— выборочное среднее.
где 
, 
— первый (нижний) и третий (верхний) квартили соответственно, 
— медиана (второй или серединный квартиль).
Относительные показатели
Известно, что коэффициент вариации может быть записан посредством долей [4] :
где 
.
где 
— математическое ожидание. Эта формула применяется для вероятностных моделей.
Примечания
 Статистические показатели | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Описательная статистика |
| ||||||||||||
| Статистический вывод и проверка гипотез |
| ||||||||||||
| Корреляция | Коэффициент корреляции Пирсона · Ранг корреляций (Коэффициент Спирмана для ранга корреляций, Коэффициент тау Кендалла для ранга корреляций) · Переменная смешивания | ||||||||||||
| Линейные модели | Основная линейная модель · Обобщённая линейная модель · Анализ вариаций · Ковариационный анализ | ||||||||||||
| Регрессия | Линейная · Нелинейная · Непараметрическая регрессия · Полупараметрическая регрессия · Логистическая регрессия | ||||||||||||
 |
.
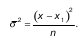
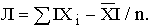
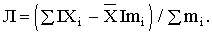
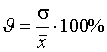
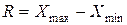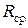– это есть средняя арифметическая из ряда размахов, полученных из серии равных по объему наблюдений. Используется в контроле качества.
,
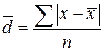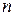– число членов ряда.
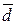– СЛО равно средней арифметической из абсолютных отклонений (модулей) признака всех единиц совокупности от средней арифметической.
,
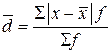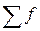– сумма частот вариационного ряда.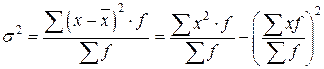
.
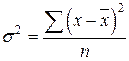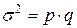
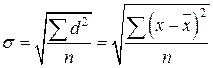– для несгруппированных данных;
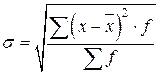– для сгруппированных данных (для вариационного ряда).
,
);
);
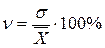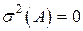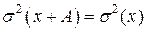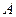, дисперсия увеличится в 
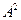раз 
;
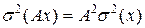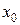на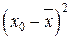 
– свойство минимальности дисперсии от средней (
).
,
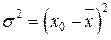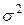
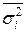
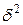
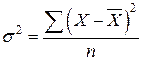
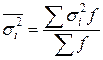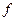– частота появления внутригрупповой дисперсии одной величины (одного размера).
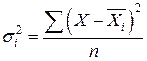– внутригрупповая 
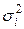— измеряет вариацию признака внутри группы, 
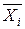— групповая средняя.
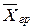вокруг общей средней 
:
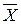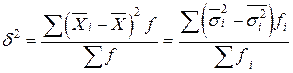
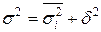
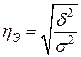– характеризует влияние группировочного признака на результативный признак (оба показателя (числитель и знаменатель) не превышают по своей величине единицы: чем больше показатели в этих пределах, тем теснее взаимосвязь между изучаемыми признаками).
; 
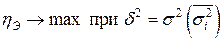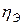– влияние других факторов равно 0.
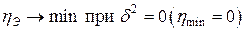– влияние признака равно 0.