Что такое lg в математике калькулятор

Вычисление десятичного логарифма

Логарифмирование — операция, которая обратна возведению в степень. Для решения задач на определение количества удесятирений применяются десятичные логарифмы.

Возведение в степень и логарифм

Мы знаем, что деление и умножение — это обратные математические операции. Если выражение A × B = C правдиво, то справедливо и выражение A = C / B или B = C / A. Для выражения со степенями все не так просто. Выражение A B = B A верно только для двух случаев: когда A и B равны единице или двойке. Во всех остальных случаях такое арифметическое выражение необратимо. Для решения показательных уравнений вида A x = B используются логарифмы.

Пусть у нас есть уравнение 3 x = 9. Для решения такого уравнения достаточно задаться вопросом: в какую степень нужно возвести тройку, чтобы получить 9? Элементарно, во вторую. В данном случае x = 2. Изменим немного уравнение и представим, что 3 x = 10. Здесь возникает сложный вопрос, как подсчитать икс, если это не целое число? Неизвестное в данном случае будет иррациональным числом, представить которое можно только с заданной степенью точности. Математики нашли элегантный способ для компактной записи таких значений. Решением уравнения 3 x = 10 будет x = log 3 10. И все, этого достаточно.

Итак, логарифм log A B — это такое число, в которое требуется возвести A, чтобы получить B. A — это основание логарифма, и оно может быть любым положительным числом. Однако существует два особенных числа, для которых были введены собственные логарифмы. Это экспонента (e = 2,71828) и число 10. Логарифмы по основанию е носят название натуральных, а по основанию 10 — десятичных.

Понятие десятичного логарифма

Десятичный логарифм lgA — это такое число, в которое требуется возвести 10, чтобы получить число A. Из программы математики средней школы известно, что любое число можно представить в виде 10 a или простыми словами в виде десятки в некоторой степени. Это достаточно четко иллюстрируется примером, когда число кратно 10:

Но что делать, если через десятку требуется представить число 2077? Здесь на сцену выходят десятичные логарифмы. При помощи логарифма мы можем записать lg2077 и любому математику станет ясно, что это за иррациональное число. Вычислить это значение приблизительно можно следующим образом. Если lg1000 = 3, а lg10000 = 4, то 3 > lg2077 > 4. Так как 2077 значительно ближе к 1 000, чем к 10 000, то и значение логарифма также будет в районе тройки, например, 3,2. Подсчитать более точное значение можно при помощи онлайн-калькулятора, которое будет равно lg2077 = 3,317436. Вычислить точное значение такого логарифма невозможно, так как оно иррационально и бесконечно.

История логарифмов

Потребность в логарифмировании возникла в 16-м веке, когда в Европе набирали обороты производство, торговля и мореплавание. Именно тогда бухгалтера и астрономы, математики и мануфактурщики столкнулись с проблемой громоздких вычислений, на решение которых уходило много времени и сил. Ученые постоянно возводили в степень и вычисляли корни, но сложность расчетов замедляла прогресс. Именно тогда математикам пришла идея заменить сложные вычисления степеней и корней на соответствующие операции умножения и деления, а затем — сложения и вычитания. Подобный ход конем позволил ученым производить операции поиска корней и возведения степень над огромными числами, складывая и вычитая при этом соответствующие логарифмы.

Первые логарифмические таблицы были созданы в 1614 году шотландским математиком Джоном Непером. Непер был профессиональным математиком, он занимался астрономией и не понаслышке знал о сложностях астрономических расчетов. Позднее знаменитый физик и астроном Пьер-Симон Лаплас говорил, что возникновение логарифмов значительно уменьшило вычислительный труд астронома и удвоило его жизнь. Логарифмические таблицы со временем совершенствовались и в итоге стали универсальным инструментом для громоздких вычислений. Математики старой школы до сих пор используют логарифмические линейки и считают в уме с такой же скоростью, с какой работают современные калькуляторы.

Если вы не застали времена, когда каждый математик имел в своем арсенале логарифмическую линейку и не умеете ими пользоваться, то предлагаем вам наш онлайн-калькулятор. Данная программа предназначена для вычисления любых логарифмов, в том числе и десятичных. Для расчетов вам потребуется выбрать в меню тип «Десятичный» и ввести значения в соответствующие ячейки. Калькулятор может вычислить собственно десятичный логарифм для числа X или вернуть значение числа X, если известен его логарифм.

Пример работы калькулятора

Расчет логарифмов

Обычно десятичные логарифмы используются для отображения графиков функций, которые имеют как очень малые, так и очень большие значения. Например, функция отображения громкости звука содержит как значения в диапазоне от 1 до 10, так и значения от 100 до 1 000 и от 1 000 до 10 000. Компактно уместить это на одном графике и разглядеть все значения громкости звука можно только при помощи логарифмической шкалы, в которой значения заменены десятичными логарифмами:

Эти значения легко вычислить при помощи калькулятора. Для рассчетов потребуется поочередно ввести в ячейку «Число» значения 10, 100, 1 000 и 10 000. При помощи таких значений на графике можно будет рассмотреть и маленькие значения от 1 до 10 и большие до 10 000.

Заключение

Десятичный логарифм — удобный математический инструмент, облегчивший жизнь многим поколениям математиков. Наш онлайн-калькулятор пригодится для вычислений выражений, которые содержат десятичные логарифмы.

Источник

Десятичный логарифм

Определение. Десятичный логарифм — логарифм по основанию 10.

Калькулятор десятичных логарифмов

Свойства десятичного логарифмов

lg( x · y ) = lg x + lg y

lg 100 = lg 10 2 = 2

lg 1000 = lg 10 3 = 3

Запишем очевидное равенство:

lg b · lg a = lg a · lg ab

Возведем 10 в соответствующие степени

10 lg b · lg a = 10 lg a · lg b

(10 lg b ) lg a = (10 lg a ) lg b

Используем формулы логарифма произведения и степени получим:

lg 6 = lg (2·3)= lg 2 + lg 3 = a + b ;

lg 30 = lg (5·2·3)= lg 5 + lg 2 + lg 3 = a + b + c ;

Вычислить log₉ 5 · log₂₅ 27.

Перейдем к основе 10:

log₉ 5 · log₂₅ 27 = lg 5 lg 9 · lg 27 lg 25

Используем свойство логарифма степени lg x n = n lg x :

lg 5 lg 9 · lg 27 lg 25 = lg 5 lg 3 2 · lg 3 3 lg 5 2 = lg 5 2 lg 3 · 3 lg 3 2 lg 5 = 3 4

Перейдем к основе 10:

log ₃₀ 8 = lg 8 lg 30 = lg 2 3 lg (3 · 10) =

Используем свойство логарифма степени, произведения, частного и то что 2= 10 5 :

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Понятия и термины

Впервые упоминание о логарифмах встречается в XIX веке в астрономических вычислениях. Сам же термин ввёл в обиход математик Спейдел. В 1893 году обозначать натуральный логарифм буквами ln предложил немецкий учёный Прингсхейм. Но лишь только в книге «Введение в анализ бесконечности» Эйлер дал определения логарифмам и описал их свойства, выделив при этом выражение с основанием равным десяти.

Существует несколько определений логарифмов. Для того чтобы разобраться в сущности термина нужно представить себе любое простое уравнение, содержащее степень. Например, 3 x = 9. Это выражение называется показательным, так как неизвестное число стоит в показателе степени. Равенство будет верным при иксе равному два. Ведь три в квадрате это девять.

Теперь можно рассмотреть другое уравнение: 3 x = 7. Если попробовать его решить, то можно обнаружить, что подобрать неизвестное значение будет довольно сложно. Интуитивно можно понять, что ответ будет располагаться между числом три в степени один и три в степени два. Искомое число и было решено назвать логарифмом. Записывается он как x = log3 7. Читается же формула как икс равный логарифму семи по основанию три.

Цифра, стоящая в нижнем регистре записи, называется основанием, а в верхней части аргументом. То есть любое выражение вида c x = k можно записать как x = logc k. Эта запись очень удобна для обозначения иррациональных чисел.

Логарифм можно записать только при выполнении условия: logp K = b, где pb = k, p > 0, k > 0, p ≠ 0. Существует три вида логарифма:

Десятичный логарифм записывают упрощённой записью: log10. Например, число два можно представить, как lg 100. Эта запись верна, так как используя определение, запись можно переписать в виде: 10 2 = 100. Для того чтобы научиться решать задачи по нахождению логарифмов нужно знать их свойства, формулы сокращённого умножения и правила вычисления степеней.

Свойства и формулы

Формулы сокращённого умножения изучают в средней школе на уроках алгебры. Учащимся предлагается выучить семь основных выражений, собранных в таблицу. С их помощью можно быстро и в уме рассчитывать квадраты даже больших чисел, что используется при нахождении логарифмов. Доказываются они просто раскрытием скобок. Из основных равенств умножения можно выделить следующие:

На этих формулах основаны свойства десятичных логарифмов. Большинство задач можно решить, зная только эти закономерности. Первое свойство вытекает из самого определения выражения: log​p ​​p v ​ ​= v. Для доказательства этого свойства можно использовать рассуждение, что если log​і ​​p​ ​= v, то i v = p. Тогда отношение logk p / logk I будет равняться: logk i v / logk I = v * logk i / logk I = v = log​і ​​p​. Что и требовалось доказать.

Второе и третье свойство помогает определить сумму логарифмов и посчитать их разницу. Согласно ему сумма выражений с одинаковым основанием равняется их произведению: logp i + logp c = logp (i * c). А также используется то что разность произведений с одинаковыми основаниями тождественна логарифму отношения: logp i − logp c = logp c * i.

Четвёртое свойство позволяет при необходимости степень выносить за знак логарифма: logk i v ​ ​ = n * logk i. Пятое правило гласит, что если в основании логарифма стоит степень, то её можно переместить за знак функции: log​k n ​​​i = ​ 1/ n​​​ ​ * log​k ​​i. В отличие от четвёртого свойства показатель степени всегда выносится как обратное число.

Следующее свойство сообщает, что если основание и аргумент имеют степень, то эти показатели можно вынести за знак выражения как дробь: log​k​ n * ​​​​i​ m ​​ =​ (m​/n) ​ * log​k​​i. При этом если степени совпадают по своему значению, это правило можно записать как log k n i n = log k i. Седьмое свойство помогает решать логарифмы с разным основанием. Так, любой логарифм можно записать в виде равенства: log k i = log c i / log c k.

Эти свойства применимы к любым видам логарифмов. При этом существует ещё одно позволяющее поменять местами основание и аргумент. Для этого нужно просто единицу разделить на логарифм: log k​ b = 1 / ​ log k b.

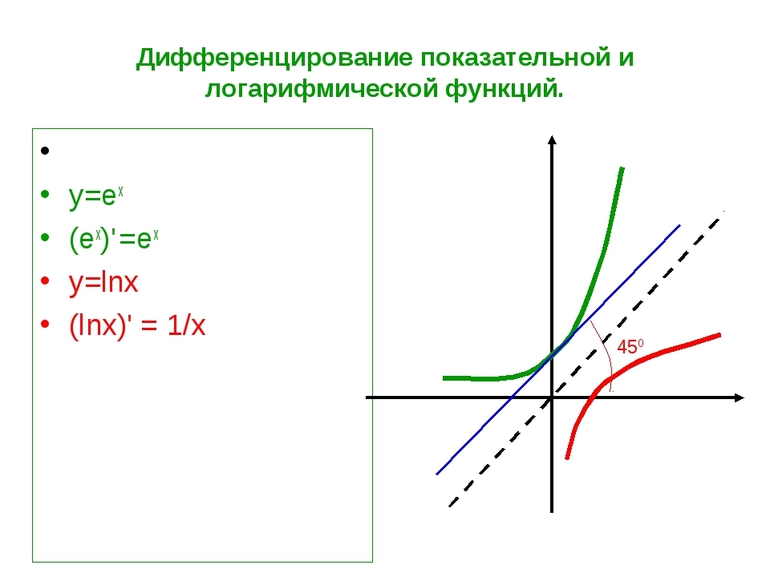
Дифференцирование и функция

Производная десятичного логарифма определяется, как отношение в числителе которого стоит единица, а в знаменателе показатель. Для доказательства этого можно рассмотреть произвольное число, которое больше единицы. Пусть имеется следующая функция: t = logc p.

Воспользовавшись свойством формулу можно упростить и записать: t’ = 1/t * logc p = (1/t) * (1/ln p) = 1 / t * ln p. То есть получить рассматриваемую функцию. Тождественным доказательством будет и метод вынесения постоянной за знак дифференцирования: (logc p)’ = (ln p / ln c)’ = ((1 / ln c ) * ln p )’ = (1/ ln c) * (1/ p) = 1 / p ln c.

Интеграл функции можно записать выражением: ∫ ln x dx = x * ln x – x + C. Находят его способом интегрирования по частям. Этим методом выражение сводится к более простому виду.

Функцию десятичного логарифма можно записать как y = lg x. График имеет вид плавной возрастающей кривой, которую ещё называют логарифмикой. К основным характеристикам функции относят:

Функция монотонная, то есть всё время она не убывает и не возрастает. Иными словами, она всегда неотрицательная или неположительная, но при этом всюду дифференцируемая. Производная для выражения находится с помощью формулы: (d/dx) lg x = lg e / x. Ось ординат обладает свойством вертикальной асимптотности, так как при лимите стремящимся к нулю логарифм по иксу будет равный минус бесконечность.

Примеры решения задач

При решении тождеств, содержащих тригонометрические функции, поможет и сборник таблиц Брадиса. Это пособие, в котором собраны ответы для чаще всего встречающихся типовых выражений.

Следующие типы примеров наиболее часто предлагаются в школе для самостоятельного решения:

Но бывает так, что самостоятельно решить задачу довольно сложно из-за громоздкости записи уравнения. При этом не так сложно провести вычисления, как правильно выбрать алгоритм решения. Поэтому в таких случаях используют так называемые онлайн-калькуляторы.

Использование онлайн-калькулятора

Использовать сервисы предлагающие услуги по вычислению десятичного логарифма, довольно удобно. Всё, что требуется от пользователя, — это интернет-канал и браузер с поддержкой флеш-технологии. Доступ к онлайн-калькуляторам предоставляется бесплатно, при этом даже нет необходимости в регистрации или указании каких-либо данных.

Онлайн-расчётчики позволяют не только получить быстрый и правильный ответ вычисления выражения любой сложности, но и предоставляют подробное решение с пояснениями. Кроме того, на страницах таких сервисов содержится краткая теория с примерами. Так что проблем с понятием, откуда взялся ответ возникнуть не должно.

Программы, используемые для расчётов, написаны на Java и включают в свой алгоритм все необходимые формулы. Пользователь, загрузив сервис должен ввести условие задачи в специально предложенную формулу и нажать кнопку «Решение» или «Вычислить». После чего буквально через две три секунды появится ответ с поэтапным решением.

Такие сервисы будут полезны не только учащимся для проверки своих знаний, но и даже инженерам, проводящим сложные вычисления. Ведь самостоятельный расчёт требует повышенного внимания и скрупулёзности. При этом любая незначительная ошибка приведёт к неправильному ответу. В то же время появление ошибки при вычислении на онлайн-калькуляторе практически невозможно.

По мнению пользователей, из нескольких десятков существующих сайтов можно выделить тройку лидеров:

Приведённые онлайн-калькуляторы для десятичного логарифма имеют интуитивно понятный интерфейс. Используемые программы написаны российскими программистами и не содержат рекламного и вредоносного кода. Решив несколько задач с помощью этих порталов, пользователь научится самостоятельно вычислять любые логарифмические уравнения. То есть калькуляторы смогут не только подтянуть знания на нужный уровень, но и даже заменить репетитора по математике.

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение логарифмических уравнений.

Этот математический калькулятор онлайн поможет вам решить логарифмическое уравнение. Программа для решения логарифмического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Введите логарифмическое уравнение
Решить уравнение

Немного теории.

Логарифмическая функция. Логарифмы

Задача 1. Найти положительный корень уравнения x 4 = 81
По определению арифметического корня имеем \( x = \sqrt[4] <81>= 3 \)

В задаче 1 неизвестным является основание степени, а в задаче 2 — показатель степени. Способ решения задачи 2 состоял в том, что левую и правую части уравнения удалось представить в виде степени с одним и тем же основанием 3. Но уже, например, уравнение 3 x = 80 таким способом решить не удаётся. Однако это уравнение имеет корень. Чтобы уметь решать такие уравнения, вводится понятие логарифма числа.
Уравнение a x = b, где a > 0, \( a \neq 1 \), b > 0, имеет единственный корень. Этот корень называют логарифмом числа b no основанию a и обозначают log_ab
Например, корнем уравнения 3 x = 81 является число 4, т.е. log₃81 = 4.

Определение. Логарифмом положительного числа b по основанию a, где a > 0, \( a \neq 1 \), называется показатель степени, в которую надо возвести число a, чтобы получить b

log₇7 = 1, так как 7 1 = 7

Определение логарифма можно записать так:

Действие нахождения логарифма числа называют логарифмированием.
Действие нахождения числа по его логарифму называют потенцированием.

Вычислить \( 3^ <-2\log_3 5>\)
Используя свойства степени и основное логарифмическое тождество, находим

Свойства логарифмов

При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них.

Пусть а > 0, \( a \neq 1 \), b > 0, c > 0, r — любое действительное число. Тогда справедливы формулы:

Десятичные и натуральные логарифмы

Для логарифмов чисел составлены специальные таблицы (таблицы логарифмов). Логарифмы вычисляют также с помощью микрокалькулятора. И в том и в другом случае находятся только десятичные или натуральные логарифмы.

Определение. Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут
lg b вместо log₁₀b

Определение. Натуральным логарифмом числа называют логарифм этого числа по основанию e, где e — иррациональное число, приближённо равное 2,7. При этом пишут ln b вместо log_eb

Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить логарифмы чисел по любому основанию.
Для этого используется формула замены основания логарифма:

Следствия из формулы замены основания логарифма.
При c = 10 и c = e получаются формулы перехода к десятичным и натуральным логарифмам:
$$ \log_a b = \frac<\lg b> <\lg a>, \;\; \log_a b = \frac<\ln b> <\ln a>$$

Логарифмическая функция, её свойства и график

В математике и её приложениях часто встречается логарифмическая функция
y = log_ax
где а — заданное число, a > 0, \( a \neq 1 \)

Логарифмическая функция обладает свойствами:
1) Область определения логарифмической функции — множество всех положительных чисел.

2) Множество значений логарифмической функции — множество всех действительных чисел.

3) Логарифмическая функция не является ограниченной.

4) Логарифмическая функция y = log_ax является возрастающей на промежутке \( (0; +\infty) \), если a > 1,
и убывающей, если 0 1, то функция y = log_ax принимает положительные значения при х > 1,
отрицательные при 0 1.

Ось Oy является вертикальной асимптотой графика функции y = log_ax

Отметим, что график любой логарифмической функции y = log_ax проходит через точку (1; 0).
При решении уравнений часто используется следующая теорема:

Логарифмические уравнения

Источник

Работа с инженерным калькулятором

Калькулятор инженерный

Используйте инженерный калькулятор для сложных расчетов с применением тригонометрических функций. Команды вводятся с помощью мыши или клавиатуры.
Инженерный калькулятор позволяет производить сложные расчеты с применением различных тригонометрических функций: синуса, косинуса, тангенса, котангенса. Калькулятор позволяет возводить числа в степень, вычислять логарифм числа.
Основные команды (цифры, умножение, деление, сложение, вычитание, равенство, сброс) можно вводить как с помощью мышки, так и с помощью цифровой клавиатуры (верхней или боковой). Подробные инструкции по работе с инженерным калькулятором смотрите внизу страницы.

Функции стандартных кнопок

Ввод команд с компьютерной клавиатуры

Для работы с калькулятором можно использовать любые цифровые клавиши: как цифровые клавиши находящиеся сверху, так и отдельные цифровые клавиши находящиеся справа.

Для ввода равно можно использовать клавишу [ Enter ];
Для стирания последнего знака используется клавиша [ Backspace ] (клавиша со стрелкой);
Для ввода знака плюс используется клавиша [ + ] сверху или на боковой клавиатуре;
Для ввода знака минус используется клавиша [ – ] сверху или на боковой клавиатуре;
Для ввода знака умножения используется клавиша [ * ] на боковой клавиатуре;
Для ввода знака деления используется клавиша [ / ] на боковой клавиатуре;
Для сброса калькулятора можно использовать клавиши [ Esc ], [ Del ] на верхней клавиатуре или [ End ] на цифровой клавиатуре.

Примеры вычислений на инженерном калькуляторе

Почему мы так решили? Наш онлайн калькулятор оперирует числами вплоть до 20 знаков после запятой, в отличие от других. Kalkpro.ru способен точно и достоверно совершить любые вычислительные операции, как простые, так и сложные.

Только корректные расчеты по всем правилам математики!

В любой момент и в любом месте под рукой, универсальный инженерный калькулятор онлайн выполнит для вас любую операцию абсолютно бесплатно, практически мгновенно, просто добавьте программу в закладки.

Всё для вашего удобства:

Содержание справки:

Комплекс операций инженерного калькулятора

Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.

Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.

Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.

Ввод цифр производится в двух вариантах:

Инструкция по функциям инженерного калькулятора

Для понимания возможностей программы мы даем вам краткую инструкцию, более подробно смотрите в примерах вычислений онлайн. Принцип работы с научным калькулятором такой: вводится число, с которым будет производиться вычисление, затем нажимается кнопка функции или операции, потом, если требуется, то еще цифра, например, степень, в конце – знак равенства.

Как пользоваться MR MC M+ M- MS

Как пользоваться инженерным калькулятором – на примерах

Как возвести в степень

Чтобы возвести, к примеру, 12^3 вводите в следующей последовательности:

12 [x y ] 3 [=]

12, клавиша «икс в степени игрик» [xy], 3, знак равенства [=]

Как найти корень кубический

Допустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:

729 [3√x] [=]

729, [ 3 √x] «кубический корень из икс», равенства [=]

Как найти корень на калькуляторе

Задача: Найти квадратный корень 36.

Решение: всё просто, нажимаем так:

36 [ y √x] 2 [=]

36, [ y √x] «корень из икса, в степени игрик», нужную нам степень 2, равно [=]

При помощи этой функции вы можете найти корень в любой степени, не только квадратный.

Как возвести в квадрат

Для возведения в квадрат онлайн вычислительная программа содержит две функции:

[x y ] «икс в степени игрик», [X 2 ] «икс в квадрате»

Последовательность ввода данных такая же, как и раньше – сначала исходную величину, затем «x^2» и знак равно, либо если не квадрат, а произвольное число, необходимо нажать функцию «x^y», затем указать необходимую степень и так же нажать знак «равно».

Например: 45 [x y ] 6 [=]

Ответ: сорок пять в шестой степ. равно 8303765625

Тригонометрический калькулятор онлайн – примеры

Как произвести онлайн расчет синусов и косинусов, тангенсов

Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами.

1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.

Для включения того или иного режима измерения нажмите нужную кнопку:

где Deg – градусы, Rad – измерение в радианах, Grad – в градах. По умолчанию включен режим расчета в градусах.

В качестве самого простого примера найдем синус 90 градусов. Нажмите:

90 [sin] [=]

Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:

60 [cos] [=]

Для их ввода необходимо переключить интерфейс, нажав [Inv], появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.

Преобразование с кнопкой Dms и Deg на калькуляторе

[Deg] позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. [Dms] производит обратный перевод – в формат «градусы; минуты; секунды».

Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:

35,140453 [Deg] [=] 35,23459166666666666666

Переведем в прежний формат: 35,23459166666666666666 [Dms] [=] 35,140453

Десятичный логарифм онлайн

Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:

1 [log] [=]

Получается 0 в итоге. Для подсчета lg100 нажмем так:

100 [log] [=]

Решение: два. Как себя проверить? Что вообще такое десятичный логарифм – log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.

Так же вычисляется натуральный логарифм, но кнопкой [ln].

Как пользоваться памятью на калькуляторе

Существующие кнопки памяти: M+, M-, MR, MS, MC.

Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.

MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.

Пример. Внесем сто сорок пять в память программы:

145 [MR]

После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:

На экране отобразится снова 145.

Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем [M+], либо [M-] для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой [MR] получится 230, а во втором, после нажатия [M-] и [MR] получится 60.

Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.

Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!

В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.

Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.

Из этой статьи вы узнаете, как пользоваться основными функциями научного (инженерного) калькулятора. Научный калькулятор пригодится при изучении алгебры, геометрии и тригонометрии.

Найдите основные функции. На калькуляторе есть несколько функций, которые понадобятся для решения алгебраических, тригонометрических, геометрических и других задач. Найдите на калькуляторе следующие функции:

Источник