Что такое группировка в математике

Группировка слагаемых

Группировка слагаемых — это объединение слагаемых в группы с помощью скобок. При группировке слагаемых обычно изменяется порядок их следования в сумме для удобства вычислений.

Метод группировки слагаемых можно применять к суммам, состоящим из трёх и более слагаемых. Группировку можно разбить на три последовательных действия:

Рассмотрим нахождение значения выражения, изображённого на картинке:

Можно просто сначала сложить первые два слагаемых, к полученной сумме прибавить третье слагаемое, а к полученному результату затем прибавить четвёртое слагаемое:

15 + 27 + 55 + 13 = 42 + 55 + 13 = 97 + 13 = 110,

но в данном случае значение выражения будет легче найти, если сначала сгруппировать слагаемые так, чтобы в сумме они давали круглые числа:

15 + 27 + 55 + 13 = (15 + 55) + (27 + 13) = 70 + 40 = 110.

Приём группировки слагаемых обычно используется для упрощения вычислений.

Пример. Вычислить значение выражений, используя приём группировки слагаемых.

3) 340 + 114 + 60 + 26;

4) 154 + 235 + 13 + 115 + 46.

1) 248 + 123 + 52 + 7 = ( 248 + 52) + ( 123 + 7) = 300 + 130 = 430;

2) 101 + 67 + 19 + 3 = ( 101 + 19) + ( 67 + 3) = 120 + 70 = 190;

3) 340 + 114 + 60 + 26 = ( 340 + 60) + ( 114 + 26) = 400 + 140 = 540;

4) 154 + 235 + 13 + 115 + 46 = ( 154 + 46) + ( 235 + 115) + 13 = 200 + 350 + 13 = 563.

Источник

Урок «Способ группировки»

Краткое описание документа:

Преобразование многочленов, состоящих из большого числа различных мономов, является одним из ключевых действий в линейной алгебре. При помощи этой процедуры решаются многие уравнения и развязываются неравенства. Правильное оперирование с многочленами позволяет также упрощать выражения функций и решать многие смежные комплексные задачи.

Поэтому в нашей серии видеоуроков мы продолжим рассматривать важнейшие аспекты преобразования полиномов, в частности, затронем такой метод, как группировку одночленов.

Как известно, одночлены представляют собой некое элементарное выражение, которое содержит переменную (или несколько переменных), числовой коэффициент и степень переменных. При этом коэффициент может быть равен нулю (буквенные значения без цифр), а переменные – отсутствовать (остается одно лишь число). Что бы перегруппировать одночлены, необходимо тщательно изучить их основу. Когда мы в предыдущем занятии выносили множитель за скобки, основа нужна была для утверждения самого множителя. В данном же случае по основе будет проводиться группировка одночленов для дальнейших преобразований.

Существует правило, согласно которому выбирается такая основа, которая имеет максимально допустимую разрядность в том случае, если выбор её не продиктован внешними условиями комплексной задачи. Важно понять, что при применении способа группировки ищутся две или больше основ – для образования двух, или больше групп одночленов. Это коренное отличие данного метода от способа вынесения множителя за скобки. Хотя, в целом, ход дальнейших действий представляет собой вынесение основы за скобки (в которых заключена группа схожих одночленов), или схожие действия. Рассмотрим применение способа группировки на практике. Допустим, нам нужно преобразовать выражение:

2ас + 3ху + 8ау – 9хс

Стоит отметить, что способ группировки очень часто может дать несколько путей решения выражения. Особенно если многочлен содержит большое количество однотипных мономов. Группировать одночлены можно в любом порядке, соблюдая лишь правило наличия общей основы. Если сгруппировать выражение можно несколькими способами, то стоит выбирать наиболее оптимальный (чаще всего, подбирая группировку так, что бы получить необходимый для дальнейших вычислений элемент). В нашем примере, сгруппируем первый и третий члены многочлена, а также второй и четвертый. При этом первая группа имеет общую основу 2а (общая переменная а, наибольший допустимый числовой коэффициент), вторая группа – 3х. Группируем одночлены, выносим основы за скобки, произведя деление и не забывая про правила сохранения знаков:

2ас + 3ху + 8ау – 9хс = 2ас + 8ау + 3ху – 9хс = 2а(с+4у) + 3х(у – 3с)

Грубо говоря, числовой коэффициент множителя можно брать в виде абсолютно любого значения. Но чаще всего подбирают такое число, чтобы оно было кратным всем одночленам группы – это позволит избежать дробей.

Рассмотрим ещё один пример, более сложный. Предположим, нам нужно разложить на множители полином вида:

Напрямую в этом выражении ничего вынести за скобки нельзя. Общий множитель для одного из членов отсутствует, а разность степеней переменных не позволяет полностью убрать х из группы первых двух мономов. Можно решить это выражение методом подбора. Представим произведение многочленов и решим его методом прямого перемножения (памятуя о строгой необходимости перемножить каждый член):

(х + а)(х + с) = х 2 + хс + ах + ас

Сгруппируем второй и третий члены полученного выражения, используя общую переменную х:

х 2 + хс + ах + ас = х 2 + х(а + с) + ас

Как заметно в видеоуроке, выражения х 2 – 8х + 15 и х 2 + х(а + с) + ас достаточно подобны между собой. Для их сравнения необходимо, чтобы коэффициент при х представлял собой сумму двух неких чисел а и с, которые в произведении дали бы свободный член полинома. Задачу нахождения этих чисел можно решить через подбор либо же использовать систему линейных уравнений:

х 2 + хс + ах + ас = х 2 – 8х + 15

х 2 + хс + ах + ас = (х + а)(х + с)

х 2 – 8х + 15 = (х + а)(х + с)

где а=-3, с=-5, подставляя значения переменных:

х 2 – 8х + 15 = (х – 5)(х – 3)

В дальнейших уроках можно будет узнать, что некоторые формулы, состоящие из стандартных переменных в многочленах, являются особой группой выражений, именуемых формулами сокращенного умножения.

Источник

Алгебра

План урока:

Вынесение общего множителя за скобки

В предыдущем уроке мы изучили умножение многочлена на одночлен. Например, произведение монома a и полинома b + c находится так:

Однако в ряде случае удобнее выполнить обратную операцию, которую можно назвать вынесением общего множителя за скобки:

Например, пусть нам надо вычислить значение полинома ab + bc при значениях переменных a = 15,6, b = 7,2, c = 2,8. Если подставить их напрямую в выражение, то получим

ab + bc = 15.6 * 7.2 + 15.6 * 2.8

что, скорее всего, не получится посчитать в уме. Если же вынести a за скобки, то получим иную запись:

ab + bc = a(b + c) = 15.6 * (7.2 + 2.8) = 15.6 * 10 = 156

В данном случае мы представили полином ab + bc как произведение двух множителей: a и b + с. Данное действие называют разложением многочлена на множители.

При этом каждый из множителей, на которые разложили многочлен, в свою очередь может быть многочленом или одночленом.

Видно, что у обоих многочленов есть общий множитель 7b. Значит, его можно вынести за скобки:

Проверить правильность вынесения множителя за скобки можно с помощью обратной операции – раскрытия скобки:

Важно понимать, что часто полином можно разложить несколькими способами, например:

5abc + 6bcd = b(5ac + 6cd) = c(5ab + 6bd) = bc(5a + 6d)

Обычно стремятся вынести, грубо говоря, «наибольший» одночлен. То есть раскладывают полином так, чтобы из оставшегося полинома больше нечего нельзя было вынести. Так, при разложении

5abc + 6bcd = b(5ac + 6cd)

в скобках осталась сумма одночленов, у которых есть общий множитель с. Если же вынести и его, то общих множителей в скобках не останется:

b(5ac + 6cd) = bc(5a + 6d)

Разберем детальнее, как находить общие множители у одночленов. Пусть надо разложить сумму

8a 3 b 4 + 12a 2 b 5 v + 16a 4 b 3 c 10

Она состоит из трех слагаемых. Сначала посмотрим на числовые коэффициенты перед ними. Это 8, 12 и 16. В 3 уроке 6 класса рассматривалась тема НОД и алгоритм его нахождения.Это наибольший общий делитель.Почти всегда его можно подобрать устно. Числовым коэффициентом общего множителя как раз будет НОД числовых коэффициентов слагаемых полинома. В данном случае это число 4.

Далее рассмотрим буквенную часть. В ней должны быть переменные, которые есть во ВСЕХ слагаемых. В данном случае это a и b, а переменная c общей не является, так как не входит в первое слагаемое.

8a 3 b 4 + 12a 2 b 5 v + 16a 4 b 3 c 10 = 4a 2 b 3 (2ab + 3b 2 c + 4a 2 c 10 )

В результате у оставшихся слагаемых 2ab, 3b 2 c, 4a 2 c 10 нет ни одной общей буквенной переменной, а у их коэффициентов 2, 3 и 4 нет общих делителей.

Выносить за скобки можно не только одночлены, но и многочлены. Например:

Еще один пример. Необходимо разложить выражение

Решение. Напомним, что знак минус меняет знаки в скобках на противоположные, поэтому

Значит, можно заменить (3x – 8y) на – (8y – 3x):

Ответ: (8y – 3x)(5t – 2s).

Запомним, что вычитаемое и уменьшаемое можно поменять местами, если изменить знак перед скобками:

Верно и обратное: минус, уже стоящий перед скобками, можно убрать, если одновременно переставить местами вычитаемое и уменьшаемое:

Этот прием часто используется при решении заданий.

Способ группировки

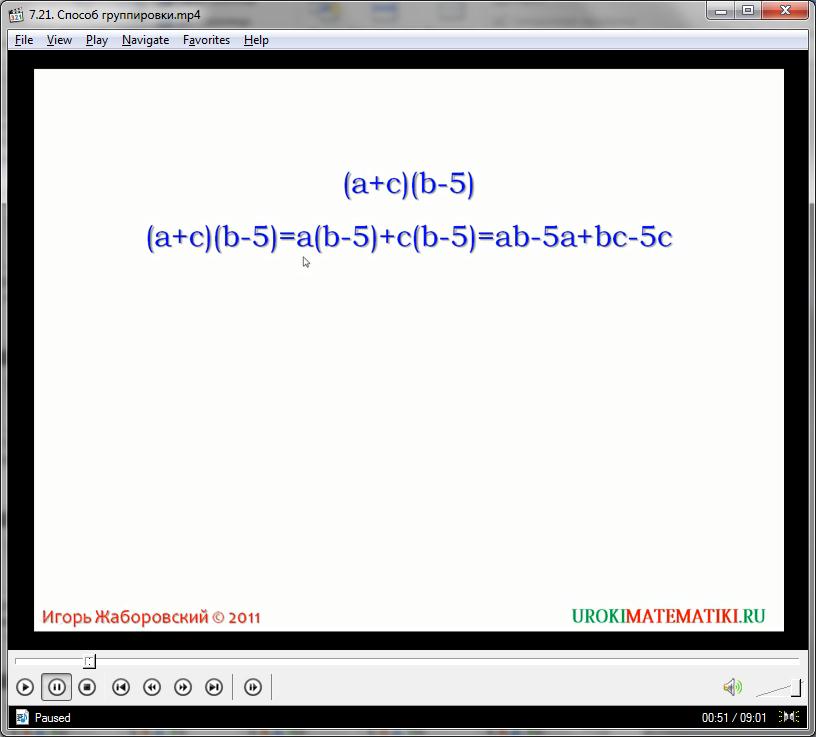
Рассмотрим ещё один способ разложения многочлена на множители, который помогает раскладывать полином. Пусть есть выражение

Вынести множитель, общий для всех четырех мономов, не получается. Однако можно представить этот полином как сумму двух многочленов, и в каждом из них вынести переменную за скобки:

Теперь можно вынести выражение b – 5:

Мы «сгруппировали» первое слагаемое со вторым, а третье с четвертым. Поэтому описанный метод называют способом группировки.

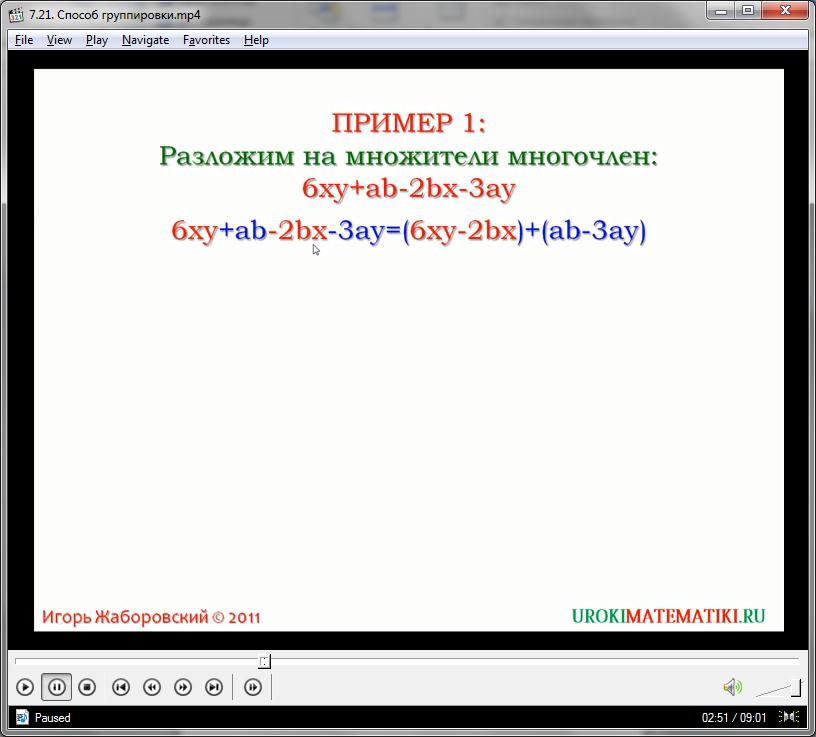
Пример. Разложим полином 6xy + ab– 2bx– 3ay.

Решение. Группировка 1-ого и 2-ого слагаемого невозможна, так как у них нет общего множителя. Поэтому поменяем местами мономы:

Разности 3y – b и b – 3y отличаются только порядком переменных. В одной из скобок его можно изменить, вынеся знак минус за скобки:

Используем эту замену:

В результате получили тождество:

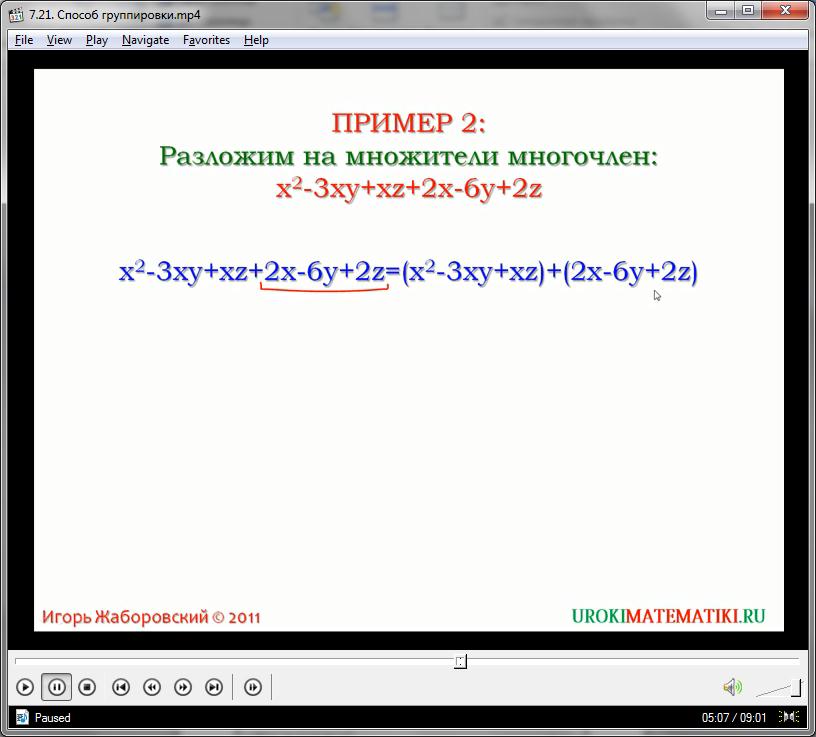
Группировать можно не только два, а вообще любое количество слагаемых. Например, в полиноме

можно сгруппировать первые три и последние 3 одночлена:

Теперь рассмотрим задание повышенной сложности

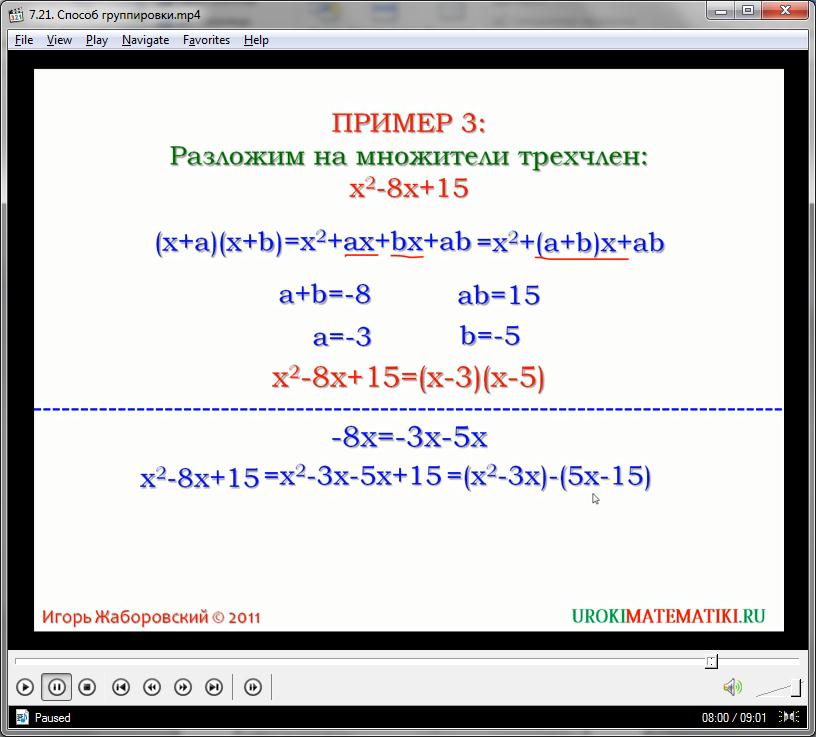
Пример. Разложите квадратный трехчлен x 2 – 8x +15.

Решение. Данный полином состоит всего из 3 одночленов, а потому, как кажется, группировку произвести не получится. Однако можно произвести такую замену:

Тогда исходный трехчлен можно представить следующим образом:

Конечно, догадаться о замене – 8х = – 3х – 5х в приведенном примере нелегко. Покажем иной ход рассуждений. Нам надо разложить полином второй степени. Как мы помним, при перемножении многочленов их степени складываются. Это значит, что если мы и сможем разложить квадратный трехчлен на два множителя, то ими окажутся два полинома 1-ой степени. Запишем произведение двух многочленов первой степени, у которых старшие коэффициенты равны 1:

(x + a)(x + b) = x 2 + xa + xb + ab = x 2 + (a + b)x + ab

Здесь за a и b мы обозначили некие произвольные числа. Чтобы это произведение равнялось исходному трехчлену x 2 – 8x +15, надо подобрать подходящие коэффициенты при переменных:

С помощью подбора можно определить, что этому условию удовлетворяют числа a= – 3 и b = – 5. Тогда

в чем можно убедиться, раскрыв скобки.

Для простоты мы рассмотрели только случай, когда у перемножаемых полиномов 1-ой степени старшие коэффициенты равны 1. Однако они могли равняться, например, 0,5 и 2. В этом случае разложение выглядело бы несколько иначе:

Однако, вынеся коэффициент 2 из первой скобки и умножив его на вторую, получили бы изначальное разложение:

В рассмотренном примере мы разложили квадратный трехчлен на два полинома первой степени. В дальнейшем нам часто придется это делать. Однако стоит отметить, что некоторые квадратные трехчлены, например,

невозможно разложить таким образом на произведение полиномов. Доказано это будет позднее.

Применение разложение многочленов на множители

Разложение полинома на множители может упростить выполнение некоторых операций. Пусть необходимо выполнить вычисление значения выражения

2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8 + 2 9

Вынесем число 2, при этом степень каждого слагаемого уменьшится на единицу:

2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8 + 2 9 = 2(1 + 2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8 )

2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8

за х. Тогда записанное выше равенство можно переписать:

Получили уравнение, решим его (см. урок уравнения):

Теперь выразим искомую нами сумму через х:

2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8 + 2 9 = x + 2 9 = 510 + 512 = 1022

При решении этой задачи мы возводили число 2 только в 9-ую степень, а все остальные операции возведения в степень удалось исключить из вычислений за счет разложения многочлена на множители. Аналогично можно составить формулу вычисления и для других подобных сумм.

Теперь вычислим значение выражения

Посчитать это напрямую достаточно сложно. Однако можно применить метод группировки:

Далее посмотрим, как можно использовать разложение полинома для доказательства делимости чисел. Пусть требуется доказать, что выражение

делится на 73. Заметим, что числа 9 и 81 являются степенями тройки:

81 = 9 2 = (3 2 ) 2 = 3 4

Зная это, произведем замену в исходном выражении:

Произведение 3 12 •73 делится на 73 (так как на него делится один из множителей), поэтому и выражение 81 4 – 9 7 + 3 12 делится на это число.

Вынесение множителей может использоваться для доказательства тождеств. Например, докажем верность равенства

(a 2 + 3a) 2 + 2(a 2 + 3a) = a(a + 1)(a + 2)(a + 3)

Для решения тождества преобразуем левую часть равенства, вынеся общий множитель:

(a 2 + 3a) 2 + 2(a 2 + 3a) = (a 2 + 3a)(a 2 + 3a) + 2(a 2 + 3a) = (a 2 + 3a)(a 2 + 3a + 2)

Далее произведем замену 3a = 2a + a:

(a 2 + 3a)(a 2 + 3a + 2) = (a 2 + 3a)(a 2 + 2a + a + 2) = (a 2 + 3a)((a 2 + 2a) + (a + 2) = (a 2 + 3a)(a(a + 2) + (a + 2)) = (a 2 + 3a)(a + 1)(a + 2) = a(a + 3)(a + z)(a + 2) = a(a + 1)(a + 2)(a + 3)

Ещё один пример. Докажем, при любых значениях переменных x и у выражение

не является положительным числом.

Решение. Вынесем общий множитель х – у:

Обратим внимание, что мы получили произведение двух похожих двучленов, отличающихся лишь порядком букв x и y. Если бы мы поменяли местами в одной из скобок переменные, то получили бы произведение двух одинаковых выражений, то есть квадрат. Но для того, чтобы поменять местами x и y, нужно перед скобкой поставить знак минус:

Тогда можно записать:

Разложение полинома помогает решать некоторые уравнения. При этом используется следующее утверждение:

Если в одной части уравнения стоит ноль, а в другой произведение множителей, то каждый из них следует приравнять нулю.

Пример. Решите уравнение (s – 1)(s + 1) = 0.

Решение. В левой части записано произведение мономов s – 1 и s + 1, а в правой – ноль. Следовательно, нулю должно равняться или s – 1, или s + 1:

Каждое из двух полученных значений переменной s является корнем уравнения, то есть оно имеет два корня.

Пример. Решите уравнение 5w 2 – 15w = 0.

Решение. Вынесем 5w:

Снова в левой части записано произведение, а в правой ноль. Продолжим решение:

Пример. Найдите корни уравнения k 3 – 8k 2 + 3k– 24 = 0.

Решение. Сгруппируем слагаемые:

k 3 – 8k 2 + 3k– 24 = 0

(k 3 – 8k 2 ) + (3k– 24) = 0

Заметим, что уравнение k 2 = – 3 решения не имеет, так как любое число в квадрате не меньше нуля. Поэтому единственным корнем исходного уравнения является k = 8.

Пример. Найдите корни уравнения

Решение: Перенесем все слагаемые в левую часть, а после сгруппируем слагаемые:

Пример. Решите уравнение

Далее решим по отдельности эти уравнения:

Теперь займемся вторым уравнением. Перед нами снова квадратный трехчлен. Чтобы разложить его на множители методом группировки, нужно представить его в виде суммы 4 слагаемых. Если произвести замену – 5t = – 2t – 3t, то дальше удастся сгруппировать слагаемые:

В результате получили, что у исходного уравнения есть 4 корня.

Источник

Конспект урока «Способ группировки» 7 класс

Учитель: Самигуллина З. Р.

Тема: Разложение многочлена на множители. Метод группировки.

1) выработать у учащихся умения выполнять разложение многочленов на множители способом группировки,

2) выработать у учащихся умения применять полученные знания для рационализации вычислений, решения уравнений, доказательства тождеств.

1) формирование алгоритмического мышления;

1) эстетическое воспитание учащихся;

2) формирование представлений о математике как части общечеловеческой культуры.

Тип урока: изучение нового материала, проблемный.

Методы обучения: проблемный, частично-поисковый.

Форма организации учебной деятельности : групповая, фронтальная, индивидуальная.

Актуализация знаний. Проверка домашнего задания.

Мотивация. Постановка учебной задачи.

Изучение нового материала.

Закрепление изученного материала.

Организация класса. Здравствуйте! Присаживайтесь. Как ваши дела? Как настроение? Рада видеть вас на уроке. Надеюсь, вы готовы к получению новых знаний? Итак, давайте начнем.

Актуализация знаний. Проверка домашнего задания.

Чтобы проверить, как вы усвоили прошлую тему и выполнили домашнее задание, я предлагаю вам ответить на несколько вопросов.. (слайд__)

Какие способы разложения многочлена на множители вы знаете?(вынесение общего множителя за скобки)

Молодцы! А теперь посмотрим на экран и устно решим примеры. (слайд__)

Вынесите за скобки общий множитель:

Молодцы! Вспомнили алгоритм, и правильно его применили.

Я вам раздам небольшие листочки. Подпишите их, и сделаем небольшой письменный тест. Можете сразу, не записывая пример, писать ответы. Первый вариант выполняет задания в левом столбце. Второй вариант выполняет задания в правом столбце.

15х + 10 y ; 9 n + 6 m ;

n (7- m ) + k (7– m ); b ( a +5) – c ( a +5);

8 m 2 n – 4 mn 3 ; 20 x ³ y ² + 4 x ² y ³;

Делаем проверку. За 5 правильных примеров ставим оценку «5», за 4 – «4», и за 3 – «3». Все ли довольны своими оценками? Поняли ли вы свои ошибки, необходимо ли разобрать примеры еще раз?

Мотивация. Постановка учебной задачи. (слайд__)

А теперь, я предлагаю вам решить несколько уравнений. Кто объяснит, как нужно решить первое уравнение? Умеем ли мы решать такие?

3) x 2 + 3x + 6 + 2x = 0.

(В первом уравнении приравниваем каждый множитель к нулю, и решаем два линейных уравнения).

(Для решения второго уравнения необходимо разложить на множители многочлен. Для этого общий множитель выносим на скобки. И решаем по аналогии с первым уравнением).

С решением третьего уравнения у нас появились трудности. Задача знакома на первый взгляд, но не решается. Мы знаем, что удобно решать уравнение, в правой части которого 0, раскладывая его левую часть на множители.

— Есть ли общий множитель у всех слагаемых? (Нет)

— Значит, этот способ разложения на множители нам не подходит? (Да)

— Как вы думаете чему мы должны сегодня научиться?

Постановка учебной задачи: Мы должны научиться раскладывать многочлен на множители другим способом.

Изучение нового материала. (слайд__)

Давайте пристально посмотрим на левую часть уравнения. Что-нибудь вы видите?

(x 2 + 3x) + (6 + 2x) = 0; (применяем сочетательный закон сложения)

Теперь у одночленов в скобках появились общие множители. В первой скобке это Х. его мы можем вынести за скобки, т.е. разложить на множители первую сумму. То же самое делаем со второй скобкой. Тут уже выносим за скобки 2. в итоге, мы получаем сумму одночленов, которые имеют общий множитель (х+3).

Т.к. в скобках стоит знак +, то мы можем поменять местами х и 3. данный множитель, мы также выносим за скобки.

Что мы получили? (Произведение).

Значит, каким способом мы многочлен представили в виде произведения? (Объединяя слагаемые в группы)

Поэтому этот способ называется способом группировки.

Данный способ применяют к многочленам, которые не имеют общего множителя для всех членов многочлена.

Сформулируем алгоритм: Чтобы разложить многочлен на множители способом группировки, нужно:

1) выполнить группировку слагаемых, имеющих общий множитель;

2) отдельно в каждой группе найти общий множитель и вынести его за скобки;

3) в получившемся выражении найти общий множитель и вынести его за скобки.

Рассмотрим пример (слайд__), в котром н еобходимо разложить на множители многочлен:

Первый способ группировки:

xy -6+3х-2 y =( xy -6)+(3 x -2 y ). Объединяем в группу первые два члена и третий и четвертый члены многочлена. Есть ли в каждой скобке общий множитель? нет. значит наша группировка неудачна.

Второй способ группировки:

Объединяем первый и третий член, второй и четвертый. Есть ли у них общие множители? Выносим за скобки. Продолжаем раскладывать.

Третий способ группировки:

Объединяем первый и четвертый члены, второй и третий. Выносим за скобки общие множители. Раскладываем на множители.

= y ( x -2)+3( x -2)=( x -2)( y +3). Группировка также выбрана удачно, мы получаем ответ. Давайте сравним ответ второго и третьего способов.

Как видите, не всегда с первого раза группировка оказывается удачной.

Рассмотрим еще несколько примеров на разложение множители, применяя метод группировки (слайд__) Для этого я предлагаю в парах разложить на множители примеры несколькими способами. Первый ряд выполняет первый пример. Второй ряд – второй, и третий ряд – третий пример.

А теперь, на тех же листочках, каждому предлагаю выбрать один из трех групп заданий.

А. Задания легкого уровня.

Б. Задания среднего уровня

3) х 2 + xy + xy 2 + y 3

С. Задания сложного уровня

Выполняете задания и сдаете мне. Я их проверю, и на следующем уроке, по вашему желанию, выставлю оценки. Также разберем все ошибки и недочеты.

Домашнее задание (слайд__): №______________ Посмотрите, все ли понятно по домашнему заданию. У кого есть вопросы?

Итог урока (слайд__). Подведем итоги урока.

а) С каким новым способом разложения многочлена на множители вы познакомились сегодня?

б) В чем он заключается?

в) К каким многочленам обычно применяют способ группировки?

8. Рефлексия (слайд__)

Я предлагаю вам ответить на вопросы:

Комфортно ли вам было на уроке?

Поняли ли вы материал урока?

С какими трудностями столкнулись?

Требовалась ли вам помощь:

Что необходимо повторить для успешной работы на следующем уроке?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-899071

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России стартует пилотный проект по реабилитации детей-инвалидов

Время чтения: 2 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Итоговое сочинение успешно написали более 97% выпускников школ

Время чтения: 2 минуты

Московские школьники победили на международной олимпиаде по информатике

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме проверят содержание учебников русского языка как иностранного

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник