Что такое группировка в алгебре

Группировка слагаемых и множителей: правило, примеры

В случае, если нам надо сложить три и более слагаемых, мы можем использовать метод тождественного преобразования, получивший название группировки слагаемых. Точно такой же метод существует и для умножения, если в примере заданы три множителя и больше. Целью этой статьи является разбор правил группировки в обоих случаях. Все теоретические положения будут проиллюстрированы примерами решений задач.

Что такое группировка слагаемых

Мы можем выполнять группировку как в буквенных, так и в числовых выражениях тогда, когда у нас есть 3 слагаемых и более. Как нужно понимать этот термин?

Группировка слагаемых основана на совместном рассмотрении нескольких слагаемых в исходной сумме. Иначе говоря, это объединение нескольких слагаемых в одну группу.

Основное правило группировки слагаемых звучит так:

При выполнении группировки мы сначала переставляем слагаемые в исходной сумме таким образом, чтобы слагаемые одной группы были рядом, после чего заключаем их в скобки.

На чем базируется данное правило? В его основе лежат переместительное и сочетательное свойство сложения.

Разберем несколько примеров.

Возьмем пример чуть сложнее.

В целом группировка слагаемых– несложное действие. Некоторая трудность может быть в том, чтобы найти в исходном выражении саму сумму и отдельные слагаемые, из которых она состоит, особенно если выражение длинное и громоздкое. После нахождения слагаемых сгруппировать их будет легко.

После нахождения всех элементов можно объединить в группу первое и третье слагаемое и получить следующее выражение:

Метод группировки необходим для рационального вычисления значений выражений. Кроме того, он широко используется для упрощения и многих других задач разной степени сложности.

1 3 + 2 7 + 2 3 + 3 7 = 1 3 + 2 3 + 2 7 + 3 7 = 1 + 5 7 = 1 5 7

Один из способов разложения многочлена на отдельные множители также основан на группировке слагаемых.

Что такое группировка множителей

Такая группировка проводится точно таким же образом, как и при сложении, единственная разница в том, что работать предстоит не с суммами, а с произведениями. Она основана на переместительном и сочетательном свойствах умножения.

Группировка множителей – это объединение в одну группу нескольких множителей.

Процесс вычисления в данном случае проводится так же: сначала мы переставляем нужные множители так, чтобы они оказались рядом, а потом расставляем скобки.

Источник

Способ группировки

Способ группировке в алгебре — один из способов разложения многочлена на множители.

Способ группировки можно разбить на два этапа:

1) Объединение членов многочлена в группы, имеющие общий множитель, и вынесение из каждой группы общего множителя (в одной из групп общего множителя может не быть).

2) Вынесение полученного общего для всех групп множителя за скобки.

Группируем первое слагаемое со вторым, третье — с четвертым.

Лучше при группировке между скобками всегда ставить знак «+»:

Общий множитель (x+7) выносим за скобки:

Группировать можно было иначе: первое слагаемое — с третьим, второе — с четвертым:

Из первых скобок выносим общий множитель x, из вторых — 7:

Общий множитель (a-3) выносим за скобки:

При любом способе группировки ответ получается одинаковый (от перестановки мест множителей произведение не меняется).

Группируем первое слагаемое со вторым, третье — с четвертым:

Из первых скобок выносим общий множитель x, из вторых — «-«:

Общий множитель (4-y) выносим за скобки:

Сгруппируем первое слагаемое со вторым и третьим, четвертое — с пятым и шестым:

Общий множитель (a²+1+b²) выносим за скобки:

Можно было группировать и по два слагаемых. Например, первое — с четвертым, второе — с пятым, третье — с шестым:

Из первых скобок выносим общий множитель a², во вторых скобках общего множителя нет, из третьих — b²:

Общий множитель (a-b) выносим за скобки. Не забываем поставить единицу на место (a-b)!

Источник

Алгебра

План урока:

Вынесение общего множителя за скобки

В предыдущем уроке мы изучили умножение многочлена на одночлен. Например, произведение монома a и полинома b + c находится так:

Однако в ряде случае удобнее выполнить обратную операцию, которую можно назвать вынесением общего множителя за скобки:

Например, пусть нам надо вычислить значение полинома ab + bc при значениях переменных a = 15,6, b = 7,2, c = 2,8. Если подставить их напрямую в выражение, то получим

ab + bc = 15.6 * 7.2 + 15.6 * 2.8

что, скорее всего, не получится посчитать в уме. Если же вынести a за скобки, то получим иную запись:

ab + bc = a(b + c) = 15.6 * (7.2 + 2.8) = 15.6 * 10 = 156

В данном случае мы представили полином ab + bc как произведение двух множителей: a и b + с. Данное действие называют разложением многочлена на множители.

При этом каждый из множителей, на которые разложили многочлен, в свою очередь может быть многочленом или одночленом.

Видно, что у обоих многочленов есть общий множитель 7b. Значит, его можно вынести за скобки:

Проверить правильность вынесения множителя за скобки можно с помощью обратной операции – раскрытия скобки:

Важно понимать, что часто полином можно разложить несколькими способами, например:

5abc + 6bcd = b(5ac + 6cd) = c(5ab + 6bd) = bc(5a + 6d)

Обычно стремятся вынести, грубо говоря, «наибольший» одночлен. То есть раскладывают полином так, чтобы из оставшегося полинома больше нечего нельзя было вынести. Так, при разложении

5abc + 6bcd = b(5ac + 6cd)

в скобках осталась сумма одночленов, у которых есть общий множитель с. Если же вынести и его, то общих множителей в скобках не останется:

b(5ac + 6cd) = bc(5a + 6d)

Разберем детальнее, как находить общие множители у одночленов. Пусть надо разложить сумму

8a 3 b 4 + 12a 2 b 5 v + 16a 4 b 3 c 10

Она состоит из трех слагаемых. Сначала посмотрим на числовые коэффициенты перед ними. Это 8, 12 и 16. В 3 уроке 6 класса рассматривалась тема НОД и алгоритм его нахождения.Это наибольший общий делитель.Почти всегда его можно подобрать устно. Числовым коэффициентом общего множителя как раз будет НОД числовых коэффициентов слагаемых полинома. В данном случае это число 4.

Далее рассмотрим буквенную часть. В ней должны быть переменные, которые есть во ВСЕХ слагаемых. В данном случае это a и b, а переменная c общей не является, так как не входит в первое слагаемое.

8a 3 b 4 + 12a 2 b 5 v + 16a 4 b 3 c 10 = 4a 2 b 3 (2ab + 3b 2 c + 4a 2 c 10 )

В результате у оставшихся слагаемых 2ab, 3b 2 c, 4a 2 c 10 нет ни одной общей буквенной переменной, а у их коэффициентов 2, 3 и 4 нет общих делителей.

Выносить за скобки можно не только одночлены, но и многочлены. Например:

Еще один пример. Необходимо разложить выражение

Решение. Напомним, что знак минус меняет знаки в скобках на противоположные, поэтому

Значит, можно заменить (3x – 8y) на – (8y – 3x):

Ответ: (8y – 3x)(5t – 2s).

Запомним, что вычитаемое и уменьшаемое можно поменять местами, если изменить знак перед скобками:

Верно и обратное: минус, уже стоящий перед скобками, можно убрать, если одновременно переставить местами вычитаемое и уменьшаемое:

Этот прием часто используется при решении заданий.

Способ группировки

Рассмотрим ещё один способ разложения многочлена на множители, который помогает раскладывать полином. Пусть есть выражение

Вынести множитель, общий для всех четырех мономов, не получается. Однако можно представить этот полином как сумму двух многочленов, и в каждом из них вынести переменную за скобки:

Теперь можно вынести выражение b – 5:

Мы «сгруппировали» первое слагаемое со вторым, а третье с четвертым. Поэтому описанный метод называют способом группировки.

Пример. Разложим полином 6xy + ab– 2bx– 3ay.

Решение. Группировка 1-ого и 2-ого слагаемого невозможна, так как у них нет общего множителя. Поэтому поменяем местами мономы:

Разности 3y – b и b – 3y отличаются только порядком переменных. В одной из скобок его можно изменить, вынеся знак минус за скобки:

Используем эту замену:

В результате получили тождество:

Группировать можно не только два, а вообще любое количество слагаемых. Например, в полиноме

можно сгруппировать первые три и последние 3 одночлена:

Теперь рассмотрим задание повышенной сложности

Пример. Разложите квадратный трехчлен x 2 – 8x +15.

Решение. Данный полином состоит всего из 3 одночленов, а потому, как кажется, группировку произвести не получится. Однако можно произвести такую замену:

Тогда исходный трехчлен можно представить следующим образом:

Конечно, догадаться о замене – 8х = – 3х – 5х в приведенном примере нелегко. Покажем иной ход рассуждений. Нам надо разложить полином второй степени. Как мы помним, при перемножении многочленов их степени складываются. Это значит, что если мы и сможем разложить квадратный трехчлен на два множителя, то ими окажутся два полинома 1-ой степени. Запишем произведение двух многочленов первой степени, у которых старшие коэффициенты равны 1:

(x + a)(x + b) = x 2 + xa + xb + ab = x 2 + (a + b)x + ab

Здесь за a и b мы обозначили некие произвольные числа. Чтобы это произведение равнялось исходному трехчлену x 2 – 8x +15, надо подобрать подходящие коэффициенты при переменных:

С помощью подбора можно определить, что этому условию удовлетворяют числа a= – 3 и b = – 5. Тогда

в чем можно убедиться, раскрыв скобки.

Для простоты мы рассмотрели только случай, когда у перемножаемых полиномов 1-ой степени старшие коэффициенты равны 1. Однако они могли равняться, например, 0,5 и 2. В этом случае разложение выглядело бы несколько иначе:

Однако, вынеся коэффициент 2 из первой скобки и умножив его на вторую, получили бы изначальное разложение:

В рассмотренном примере мы разложили квадратный трехчлен на два полинома первой степени. В дальнейшем нам часто придется это делать. Однако стоит отметить, что некоторые квадратные трехчлены, например,

невозможно разложить таким образом на произведение полиномов. Доказано это будет позднее.

Применение разложение многочленов на множители

Разложение полинома на множители может упростить выполнение некоторых операций. Пусть необходимо выполнить вычисление значения выражения

2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8 + 2 9

Вынесем число 2, при этом степень каждого слагаемого уменьшится на единицу:

2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8 + 2 9 = 2(1 + 2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8 )

2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8

за х. Тогда записанное выше равенство можно переписать:

Получили уравнение, решим его (см. урок уравнения):

Теперь выразим искомую нами сумму через х:

2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8 + 2 9 = x + 2 9 = 510 + 512 = 1022

При решении этой задачи мы возводили число 2 только в 9-ую степень, а все остальные операции возведения в степень удалось исключить из вычислений за счет разложения многочлена на множители. Аналогично можно составить формулу вычисления и для других подобных сумм.

Теперь вычислим значение выражения

Посчитать это напрямую достаточно сложно. Однако можно применить метод группировки:

Далее посмотрим, как можно использовать разложение полинома для доказательства делимости чисел. Пусть требуется доказать, что выражение

делится на 73. Заметим, что числа 9 и 81 являются степенями тройки:

81 = 9 2 = (3 2 ) 2 = 3 4

Зная это, произведем замену в исходном выражении:

Произведение 3 12 •73 делится на 73 (так как на него делится один из множителей), поэтому и выражение 81 4 – 9 7 + 3 12 делится на это число.

Вынесение множителей может использоваться для доказательства тождеств. Например, докажем верность равенства

(a 2 + 3a) 2 + 2(a 2 + 3a) = a(a + 1)(a + 2)(a + 3)

Для решения тождества преобразуем левую часть равенства, вынеся общий множитель:

(a 2 + 3a) 2 + 2(a 2 + 3a) = (a 2 + 3a)(a 2 + 3a) + 2(a 2 + 3a) = (a 2 + 3a)(a 2 + 3a + 2)

Далее произведем замену 3a = 2a + a:

(a 2 + 3a)(a 2 + 3a + 2) = (a 2 + 3a)(a 2 + 2a + a + 2) = (a 2 + 3a)((a 2 + 2a) + (a + 2) = (a 2 + 3a)(a(a + 2) + (a + 2)) = (a 2 + 3a)(a + 1)(a + 2) = a(a + 3)(a + z)(a + 2) = a(a + 1)(a + 2)(a + 3)

Ещё один пример. Докажем, при любых значениях переменных x и у выражение

не является положительным числом.

Решение. Вынесем общий множитель х – у:

Обратим внимание, что мы получили произведение двух похожих двучленов, отличающихся лишь порядком букв x и y. Если бы мы поменяли местами в одной из скобок переменные, то получили бы произведение двух одинаковых выражений, то есть квадрат. Но для того, чтобы поменять местами x и y, нужно перед скобкой поставить знак минус:

Тогда можно записать:

Разложение полинома помогает решать некоторые уравнения. При этом используется следующее утверждение:

Если в одной части уравнения стоит ноль, а в другой произведение множителей, то каждый из них следует приравнять нулю.

Пример. Решите уравнение (s – 1)(s + 1) = 0.

Решение. В левой части записано произведение мономов s – 1 и s + 1, а в правой – ноль. Следовательно, нулю должно равняться или s – 1, или s + 1:

Каждое из двух полученных значений переменной s является корнем уравнения, то есть оно имеет два корня.

Пример. Решите уравнение 5w 2 – 15w = 0.

Решение. Вынесем 5w:

Снова в левой части записано произведение, а в правой ноль. Продолжим решение:

Пример. Найдите корни уравнения k 3 – 8k 2 + 3k– 24 = 0.

Решение. Сгруппируем слагаемые:

k 3 – 8k 2 + 3k– 24 = 0

(k 3 – 8k 2 ) + (3k– 24) = 0

Заметим, что уравнение k 2 = – 3 решения не имеет, так как любое число в квадрате не меньше нуля. Поэтому единственным корнем исходного уравнения является k = 8.

Пример. Найдите корни уравнения

Решение: Перенесем все слагаемые в левую часть, а после сгруппируем слагаемые:

Пример. Решите уравнение

Далее решим по отдельности эти уравнения:

Теперь займемся вторым уравнением. Перед нами снова квадратный трехчлен. Чтобы разложить его на множители методом группировки, нужно представить его в виде суммы 4 слагаемых. Если произвести замену – 5t = – 2t – 3t, то дальше удастся сгруппировать слагаемые:

В результате получили, что у исходного уравнения есть 4 корня.

Источник

Способ группировки

Кроме вынесения общего множителя за скобки существует еще один способ разложения многочлена на множители — способ группировки.

Этот способ разложения на множители считается более сложным, поэтому перед его изучением, убедитесь, что вы уверенно выносите общий множитель за скобки.

Чтобы разложить многочлен на множители способом группировки, необходимо сделать следующее.

Рассмотрим пример разложения многочлена на множители способом группировки.

Примеры способа группировки

Рассмотрим пример. Требуется разложить многочлен на множители, используя способ группировки.

Первый способ

Обратим внимание, что в двух одночленах повторяется « y 2 » и « z 2 ». Подчеркнем повторяющиеся одночлены и запишем их друг за другом. Затем вынесем общий множитель у каждой группы одночленов.

48x z 2 + 32x y 2 − 15 z 2 − 10 y 2 = 48x z 2 − 15 z 2 + 32x y 2 − 10 y 2 = 3z 2 (16x − 5) + 2y 2 (16x − 5) =
= (16x − 5)(3z 2 + 2y 2 )

Второй способ

Запишем пример еще раз. Теперь обратим внимание, что в первых двух одночленах повторяется « x ». Подчеркнем повторяющиеся одночлены. Вынесем общий множитель у каждой группы одночленов.

48 x z 2 + 32 x y 2 − 15z 2 − 10y 2 = 16x(3z 2 + 2y 2 ) − 5(3z 2 + 2y 2 ) = (3z 2 + 2y 2 )(16x − 5)

В итоге получился такой же ответ, как и при первом способе.

Рассмотрим еще один пример разложения многочлена способом группировки.

Смена знаков в скобках

Иногда для вынесения общего многочлена требуется сменить все знаки одночленов в скобках на противоположные.

Для этого за скобки выносится знак « − », а в скобках у всех одночленов меняются знаки на противоположные.

2ab 2 − 3x + 1 = −( − 2ab 2 + 3x − 1)

Рассмотрим пример способа группировки, где для вынесения общего многочлена, нам потрубуется выполнить смену знаков в скобках.

Источник

Разложение многочлена способом группировки

Основные понятия

Мы знаем, что слово «множитель» происходит от слова «умножать».

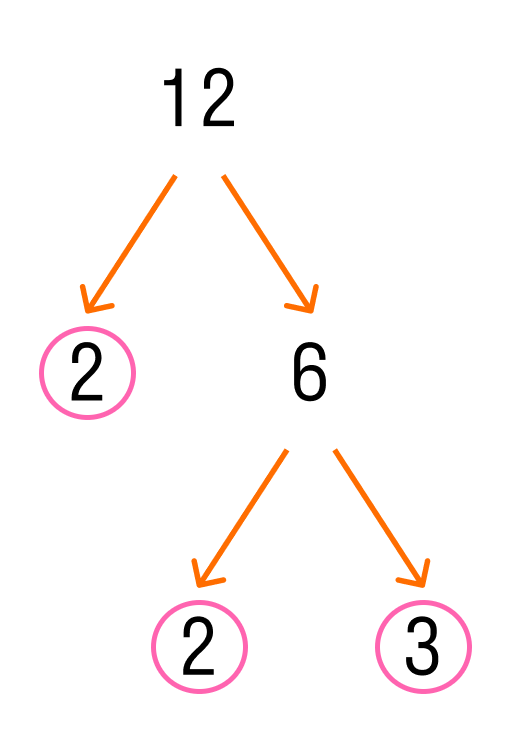
Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.

Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:

Так выглядит пошаговое разложение на множители. Числа, которые обведены в кружок на картинке — это множители, которые дальше разложить уже нельзя.

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

5 способов разложения многочлена на множители

Способ группировки множителей

Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена.

Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.

Разложить на множители методом группировки можно в три этапа:

Объединить члены многочлена в группы можно по-разному. И не всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.

Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.

Заметим, что в первой группе повторяется p, а во второй — d.

Вынесем в первой группе общий множитель p, а во второй общий множитель d.

Вынесем его за скобки:

Группировка множителей выполнена.

Заметим, что в первой группе повторяется u, а во второй — b.

Вынесем в первой группе общий множитель u, а во второй общий множитель b.

Заметим, что общий множитель (p + d).

Вынесем его за скобки:

Группировка множителей выполнена.

От перестановки мест множителей произведение не меняется, поэтому оба ответа верны:

Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.

Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.

Проверим как это на следующем примере.

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Источник