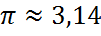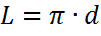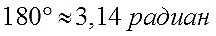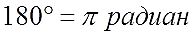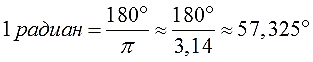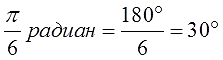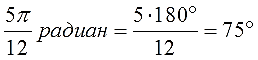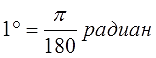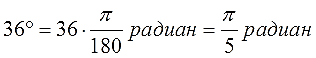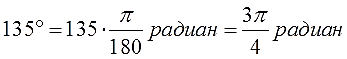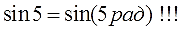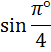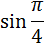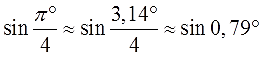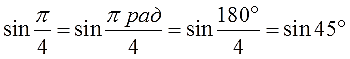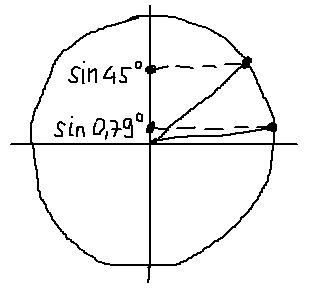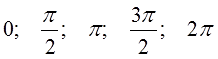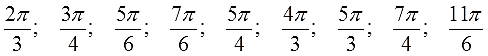Что такое градусы в математике
ГРАДУС
Смотреть что такое «ГРАДУС» в других словарях:
ГРАДУС — (лат. gradus степень, ступень, мера). 1) одна из равных частей, на которые делится окружность (обыкновенно 1/360 часть). В физике: каждая из равных частей, на которые делится шкала термометра, барометра и др. приборов. 3) в древн. Руси: ученая… … Словарь иностранных слов русского языка
ГРАДУС — ГРАДУС, условная единица, к рой пользуются при измерении самых разнообразных величин, например: температуры, жесткости, кислотности, солености, крепости; градус как единица измерения угловых величин, географический градус и др. Градус… … Большая медицинская энциклопедия
ГРАДУС — (лат. gradus шаг ступень, степень), 1) общее наименование различных единиц температуры, соответствующих разным температурным шкалам. Различают градус шкалы Кельвина, или кельвин (К), градус Цельсия (.С), градусы Реомюра (.R), Фаренгейта (.F). 1К … Большой Энциклопедический словарь
градус — ступень (Даль) См. степень. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. градус высота, степень, ступень; лигрил, десцендент, крепость, мера Словарь русских синоним … Словарь синонимов
ГРАДУС — муж. степень, ступень. Окружность круга делится на 360 градусов, которые и служат мерою для дуги, определяя, какую часть окружности она составляет, и мерою для углов, измеряемых дугою. Градус великого круга земли содержит около 105 верст или 60… … Толковый словарь Даля
ГРАДУС — (от латинского gradus шаг, ступень, степень), 1) общее наименование различных единиц температуры, соответствующих разным температурным шкалам. Различают градусные шкалы Кельвина, или кельвин (К), градус Цельсия (шC), градусы Реомюра (шR),… … Современная энциклопедия
ГРАДУС — ГРАДУС, в математике единица угловой меры, равная одной тристашестидесятой (1/360) части полного круга (360°). Один градус записывается как 1°, он подразделяется на 60 частей, называемых минутами («дуговыми минутами»), которые обозначаются как 1… … Научно-технический энциклопедический словарь
ГРАДУС — ГРАДУС, градуса, муж. (лат. gradus ступень, шаг) (научн.; условно обозначается вверху цифры справа маленьким кружком). 1. Единица измерения дуг и углов, равная 1/360 окружности. Угол в 45 градусов или в 45°. Градус широты. 2. Деление на шкале… … Толковый словарь Ушакова
ГРАДУС — (от лат. gradus шаг, ступень, степень) температурный, общее наименование разл. ед. темп ры, соответствующих разным температурным шкалам. Различают Г. шкалы Кельвина, или кельвин (К), градус Цельсия (°С), Реомюра (°R), Фаренгейта (°F), Ранкина… … Физическая энциклопедия
ГРАДУС — (Degree) 1. Единица измерения угла или дуги, равная 1/90 прямого угла или 1/360 окружности (см. Угол). Применяется для измерения углов, дуг, меридианов, параллелей, широт, долгот, азимутов и т. д. Угол в 1° образуется двумя радиусами,… … Морской словарь
градус — degree Grad 1).Одиниця виміру температури. Розрізняють Г. шкали Кельвіна (К), Цельсія (ОС), Реомюра (ОR), Фаренгейта (ОF). 1 К = 1 ОС = 0,8 ОR = 1,8 ОF. 2). Позасистемна одиниця вимірювання плоского кута, яка допущена міжнародним стандартом для… … Гірничий енциклопедичний словник
ГРАДУС
Смотреть что такое «ГРАДУС» в других словарях:
ГРАДУС — (лат. gradus степень, ступень, мера). 1) одна из равных частей, на которые делится окружность (обыкновенно 1/360 часть). В физике: каждая из равных частей, на которые делится шкала термометра, барометра и др. приборов. 3) в древн. Руси: ученая… … Словарь иностранных слов русского языка
ГРАДУС — ГРАДУС, условная единица, к рой пользуются при измерении самых разнообразных величин, например: температуры, жесткости, кислотности, солености, крепости; градус как единица измерения угловых величин, географический градус и др. Градус… … Большая медицинская энциклопедия
ГРАДУС — (лат. gradus шаг ступень, степень), 1) общее наименование различных единиц температуры, соответствующих разным температурным шкалам. Различают градус шкалы Кельвина, или кельвин (К), градус Цельсия (.С), градусы Реомюра (.R), Фаренгейта (.F). 1К … Большой Энциклопедический словарь
градус — ступень (Даль) См. степень. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. градус высота, степень, ступень; лигрил, десцендент, крепость, мера Словарь русских синоним … Словарь синонимов
ГРАДУС — муж. степень, ступень. Окружность круга делится на 360 градусов, которые и служат мерою для дуги, определяя, какую часть окружности она составляет, и мерою для углов, измеряемых дугою. Градус великого круга земли содержит около 105 верст или 60… … Толковый словарь Даля
ГРАДУС — (от латинского gradus шаг, ступень, степень), 1) общее наименование различных единиц температуры, соответствующих разным температурным шкалам. Различают градусные шкалы Кельвина, или кельвин (К), градус Цельсия (шC), градусы Реомюра (шR),… … Современная энциклопедия
ГРАДУС — ГРАДУС, градуса, муж. (лат. gradus ступень, шаг) (научн.; условно обозначается вверху цифры справа маленьким кружком). 1. Единица измерения дуг и углов, равная 1/360 окружности. Угол в 45 градусов или в 45°. Градус широты. 2. Деление на шкале… … Толковый словарь Ушакова
ГРАДУС — (от лат. gradus шаг, ступень, степень) температурный, общее наименование разл. ед. темп ры, соответствующих разным температурным шкалам. Различают Г. шкалы Кельвина, или кельвин (К), градус Цельсия (°С), Реомюра (°R), Фаренгейта (°F), Ранкина… … Физическая энциклопедия
ГРАДУС — (Degree) 1. Единица измерения угла или дуги, равная 1/90 прямого угла или 1/360 окружности (см. Угол). Применяется для измерения углов, дуг, меридианов, параллелей, широт, долгот, азимутов и т. д. Угол в 1° образуется двумя радиусами,… … Морской словарь
градус — degree Grad 1).Одиниця виміру температури. Розрізняють Г. шкали Кельвіна (К), Цельсія (ОС), Реомюра (ОR), Фаренгейта (ОF). 1 К = 1 ОС = 0,8 ОR = 1,8 ОF. 2). Позасистемна одиниця вимірювання плоского кута, яка допущена міжнародним стандартом для… … Гірничий енциклопедичний словник
Углы. Градусная мера угла.
Мерой угла является размер поворота луча около точки как центра вращения.
Что такое градусная мера угла? Градусной мерой угла является число больше нуля, которое показывает,
величина, которая отражает число градусов, минут и секунд между двумя сторонами угла.
У любого угла существует определенная градусная мера, которая больше 0. Развернутый угол = 180°.
Градусная мера угла соответствует сумме градусных мер углов, разбиваемый всяким лучом, который
проходит между его сторонами.
От всякого луча в необходимую полуплоскость есть возможность отложить угол с необходимой градусной
мерой, меньше чем 180°, и только 1.
Мерой плоского угла, который является элементом полуплоскости, является градусная мера угла с теми же
где α – градусная мера дополнительного плоского угла.
2 угла будут называться равными, когда их градусные меры одинаковы.
Свойства углов.
который проходит меж его сторонами.
мерой, меньше чем 180°, и только один.
Как найти градусную меру угла?
1 градус (°) — это угол, равный 1/180 части развернутого угла. Если выразиться по другому, если возьмем
развернутый угол и поделим его на 180 одинаковых меж собой частей-углов, то любой такой маленький угол
будет соответствовать 1 градусу. Размер остальных углов вычисляется тем, какой число этих маленьких
углов возможно разместить внутри угла, который измеряется.
Т.о., развернутый угол = 180°, прямой угол = 90°, острые углы меньше, чем 90°, а тупые — больше,
Если угол невозможно измерить точно в целых градусах, то не обязательно использовать минуты и секунды.
Можно пользоваться дробными значениями градуса. Например, 96,5°.
Известно, что минуты и секунды легко переводятся в градусы, выражая их в долях градуса.
Например, 30′ = (30/60)° или 0,5°. А 0,3° = (0,3 * 60)’ или 18′. Т.о., пользоваться минутами и секундами —
Измерение углов: градусы и радианы
Для измерения углов принято использовать две основные единицы: градусы и радианы.
Начнем с привычных градусов.
Полный круг составляет 360 градусов – это мы все знаем.
А вот в часе 60 минут, в круге 360 градусов. И в сутках 24 часа. Древние шумеры умудрились придумать двенадцатеричную систему счисления! И при этом они тоже считали по пальцам. Нет, у них не было по 6 пальцев на каждой руке. Просто считали не пальцы, а фаланги четырех пальцев (кроме большого).
Кстати, круг легко делится именно на 6 частей (умеете?). А число 12 (дюжина) делится на 2, 3, 4, 6 и, собственно, 12.
И это не все. Древние шумерские астрономы обнаружили, что в день равноденствия Солнце встает почти точно на Востоке и заходит почти точно на Западе, причем от восхода до заката проходит по небу путь, в 360 раз больший, чем видимый с Земли диаметр Солнца. Небесную полуокружность разделили на 180 градусов.
Точнее, угловой диаметр Солнца равен примерно 32 угловых минуты, то есть чуть больше 0,5 градуса. Он еще и немного меняется в течение года из-за того, что орбита Земли не круговая, а эллиптическая.
Так что утверждение о том, что в День равноденствия Солнце проходит по небу путь, равный 360 своим «шагам» (то есть 360 видимым диаметрам солнца) – верно с некоторой точностью.
Конечно, древние астрономы наблюдали не только за движением Солнца. Они заметили, что яркая планета Юпитер совершает полный оборот вокруг Солнца за 12 лет. Точнее, не 12, а 11,86 лет, но уж очень им хотелось округлить до своего любимого числа.
Да что там Юпитер! Посмотрим на Луну. Юпитер на небе еще и не каждый найдет (а вы сможете?) – зато Луну, особенно полную, трудно не заметить! Месяц – промежуток от полнолуния до полнолуния – равен примерно 29,5 суток. Почти 30, верно?
Наша Земля совершает полный оборот вокруг Солнца за 365 дней (точнее, за 365,242 суток), и это – солнечный год.
И тогда лунный год – это 12 месяцев, в каждом месяце 30 дней (округлили), вот и получается 360 дней в году, почти столько же, сколько в солнечном, в котором 365 дней.
«Может быть, боги хотели сделать в году ровно 360 дней, но им кто-нибудь помешал, вот и получилось 365». Возможно, так и рассуждали древние астрономы, деля круг на 360 частей, 360 градусов. Тем более, что 360 – число, имеющее целых 24 делителя.
Число 360 делится на 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 и 360. Очень удобно делить 360 градусов на части!
Обозначается: 360°. Этот кружок вверху – специальный символ для обозначения градуса.
Есть и другая мера измерения углов – радианная.
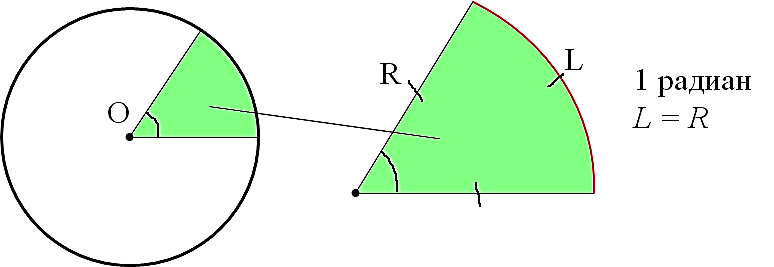
1 радиан – центральный угол, опирающийся на дугу, равную радиусу окружности.
Как перевести градусы в радианы и наоборот?
Составим пропорцию. Длина окружности так относится к длине дуги на нашем рисунке, как – к величине угла, опирающегося на эту дугу, то есть к углу в 1 радиан.
Слева в нашей пропорции углы, справа – длина полной окружности и длина отмеченной на рисунке дуги.
Из этой пропорции получаем, что радиан. Значит, полный круг – это радиан. Тогда полкруга – это радиан, четверть круга (то есть ) – это радиан.
Любой угол, выраженный в градусах, можно перевести в радианы. И наоборот, 1 радиан приблизительно равен 57 градусам.
Что такое один градус? Что такое один радиан? Перевод радианов в градусы и обратно.
В прошлый раз мы с вами ответили на первый вопрос, касаемый работы с углами. А именно — как отсчитываются углы. Рассмотрели положительные и отрицательные углы, а также углы, большие 360 градусов. И на круге углы порисовали.)
В этом же уроке настал черёд ответить на второй вопрос, связанный с измерением углов. Здесь мы разберёмся с загадочными радианами и особенно — с пресловутым числом «пи», которое будет мозолить нам глаза на протяжении всего дальнейшего изучения тригонометрии. Поймём, что это за число, откуда оно берётся и как с ним работать. И задания порешаем, само собой. Стандартные и не очень…)
Разберёмся? Ну сколько же можно бояться числа «пи», в конце-то концов!)
Итак, в чём же измеряются углы в математике? Начнём с привычного и знакомого. С градусов.
Что такое один градус? Градусная мера угла.
К градусам вы уже попривыкли. Геометрию изучаете, да и в жизни постоянно сталкиваетесь. Например, «повернул на 90 градусов».) Короче, градус — штука простая и понятная.
Вы и вправду так думаете? Тогда сможете сказать мне, что такое градус? Нет, гуглить и потрошить Википедию не надо. Ну как, слабо с ходу? Вот так-то…
Начнём издалека. С древнейших времён. А именно — с двух очагов древних цивилизаций Вавилона и Египта.)
Градус — это 1/360 часть окружности. И всё!
Придумали градусы в Древнем Вавилоне.) Как? Очень просто! Просто взяли да разбили окружность на 360 равных кусочков. Почему именно на 360? А не на 100 или на 1000? Вроде бы, число 100 поровнее, чем 360… Вопрос хороший.
Основная версия — астрономическая. Ведь число 360 очень близко к числу дней в году! А для наблюдений за Солнцем, Луной и звёздами это было оч-чень удобно.)
Кроме того, в астрономии (а также строительстве, землемерии и прочих смежных областях) очень удобно делить окружность на равные части. А теперь давайте прикинем чисто математически, на какие числа делится нацело 100 и на какие — 360? И в каком из вариантов этих делителей нацело больше? А людям такое деление очень удобно, да…)
Что такое число «пи»? Как оно возникло?
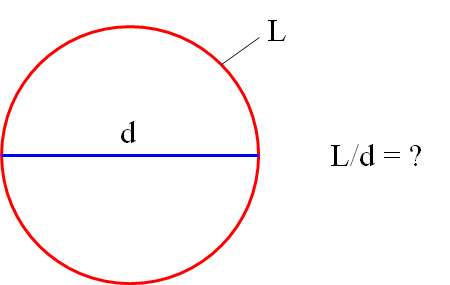
А теперь переместимся из Древнего Вавилона в Древний Египет. Примерно в то же самое время там разгадывали другую загадку. Не менее интересную, чем вопрос, на сколько частей бить окружность. А именно — во сколько раз длина окружности больше её диаметра? Или по-другому: чему равна длина окружности с диаметром, равным единице?
И так измеряли и сяк… Каждый раз получалось чуть-чуть больше трёх. Но как-то коряво получалось, неровно…
Но они, египтяне, ни в чём не виноваты. После них математики всех мастей продолжали мучиться аж до 18 века! Пока в 1767 году окончательно не доказали, что, как бы мелко ни нарезать окружность на равные кусочки, из таких кусочков сложить точно длину диаметра нельзя. Принципиально нельзя. Только лишь примерно.
Нет, конечно же, во сколько раз длина окружности больше её диаметра установили давным-давно. Но, опять же, примерно… В 3,141592653… раза.
Это число — и есть число «пи» собственной персоной.) Да уж… Корявое так корявое… После запятой — бесконечное число цифр безо всякого порядка, безо всякой логики. В математике такие числа называются иррациональными. И на сегодняшний день доказательство факта иррациональности числа «пи» занимает аж десять (!) лекций на 4-м курсе мехмата МГУ… Этот факт, кстати, и означает, что из одинаковых кусочков окружности её диаметр точно не сложить. Никак. И никогда…
Конечно, рациональные приближения числа «пи» известны людям ещё со времён Архимеда. Например:
22/7 = 3,14285714…
377/120 = 3,14166667…
355/113 = 3,14159292…
Сейчас, в век суперкомпьютеров, погоня за десятичными знаками числа «пи» не стихает, и на сегодняшний день человечеству известно уже два квадриллиона (!) знаков этого числа…
Но нам для практического применения такая сверхточность совершенно не требуется. Чаще всего достаточно запомнить всего лишь две цифры после запятой.
Вот и всё. Раз уж нам ясно, что длина окружности больше её диаметра в «пи» раз, то можно записать (и запомнить) точную формулу для длины окружности:
Здесь L — длина окружности, а d — её диаметр.
В геометрии всяко пригодится.)
Для общего развития скажу, что число «пи» сидит не только в геометрии или тригонометрии. Оно возникает в самых различных разделах высшей математики. В интегралах, например. Или в теории вероятностей. Или в теории комплексных чисел, а также рядов. Само по себе возникает, хотим мы того или нет… Поступите в ВУЗ — убедитесь лично.)
Ну а теперь снова вернёмся к старым добрым градусам. Как мы помним, один градус — это 1/360 часть окружности. С исторической и практической точек зрения людям такое деление на 360 равных частей оказалось очень даже удобно, но…
Как выяснилось гораздо позже Древнего Вавилона, градусы удобны далеко не всем. Например, высшей математике они ой как неудобны! Высшая математика — дама серьёзная. По законам природы устроена. И она справедливо заявляет: «Сегодня вы на 360 частей круг разбили, завтра — на 100 разобьёте, послезавтра — на 250… А мне что делать? Каждый раз под ваши хотелки подстраиваться?»
Против природы не попрёшь… Пришлось прислушаться и уступить. И ввести новую меру угла, не зависящую от наших хотелок. )
Итак, знакомьтесь — радиан!
Что такое один радиан? Радианная мера угла.
В основе определения радиана — та же самая окружность. Угол в 1 радиан — это угол, который отсекает от окружности дугу, длина которой (L) равна радиусу окружности (R). И всё!
Причём величина угла в один радиан не зависит от радиуса окружности! Никак. Можно нарисовать очень большую окружность, можно очень маленькую. Но угол, отсекающий от окружности дугу, равную радиусу, никогда не изменит своей величины и будет составлять ровно один радиан. Всегда. Это важно.)
Запоминаем:
Угол в один радиан — это угол, вырезающий из окружности дугу, равную радиусу окружности. Величина угла в 1 радиан не зависит от радиуса окружности.
Кстати говоря, градусная мера угла тоже не зависит от радиуса окружности. Большая окружность, маленькая — углу в один градус без разницы. Но градус — это величина, искусственно придуманная людьми для их личного удобства! Древними вавилонянами, если мы помним.) 1/360 часть окружности. Так уж сложилось чисто исторически. А если бы по каким-то причинам договорились на 100 частей разбить окружность? Или на 200? Кто знает, что тогда называлось бы градусом сегодня… Вот на сколько частей разобьём окружность, такой «градус» и получим. А вот радиан — штука универсальная!) К способу разбиения окружности никак не привязан. Строго дуга, равная радиусу! И чем больше радиус, тем больше (по длине) будет и соответствующая вырезаемая дуга. И наоборот. Но сама величина угла в один радиан не меняется. И разбиение окружности (любой!) радианами — всегда одинаковое. И сейчас мы в этом лично убедимся.)
Как переводить радианы в градусы и обратно?
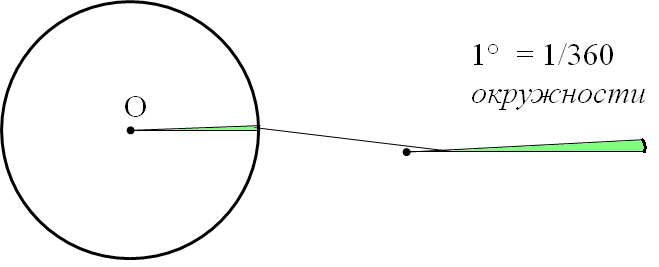
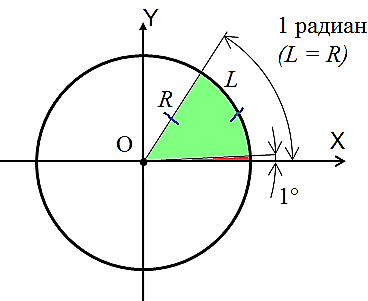
К этому моменту вам уже должно быть интуитивно понятно, что один радиан существенно больше одного градуса. Всё-таки непонятно? Тогда смотрим снова на картинку:
Будем считать, что малюсенький красный угол имеет величину примерно один градус. Совсем крохотный уголок, почти и нет его… А большой зелёный угол — примерно один радиан! Чувствуете разницу?) Конечно же, один радиан сильно больше одного градуса…
А вот теперь начинается самое интересное! Вопрос: а во сколько раз один радиан больше одного градуса? Или сколько градусов в одном радиане? Сейчас выясним!)
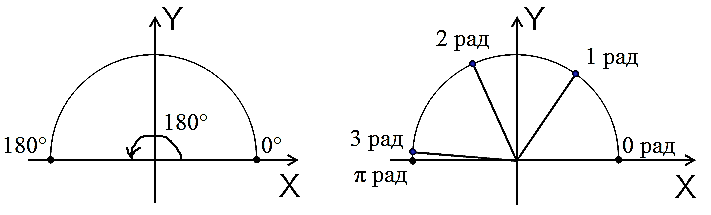
Смотрим на очередные картинки:
На картинке слева изображён полукруг. Обычный развёрнутый угол величиной 180°. А вот на картинке справа — тот же самый полукруг, но нарезанный радианами! Видно, что в 180° помещается примерно три с хвостиком радиана.
Вопрос на засыпку: как вы думаете, чему равен этот хвостик?)
Да! Он равен 0,141592653… Привет, число «пи», вот мы про тебя и вспомнили!)
Стало быть, в 180° укладывается 3,141592653… радиан. Понятное дело, что каждый раз писать такое длинное число неудобно, поэтому пишут приближённо:
Вот и всё. Вот и весь секрет тотального присутствия числа «пи» в тригонометрии. Эту простую формулку надо знать железно. Уловили?)
Так сколько же градусов в одном радиане? Не вопрос! Если в «пи» радианах содержится 180 градусов, то сколько же тогда градусов сидит в одном радиане? Правильно, в «пи» раз меньше! То есть меньше примерно в 3,14 раза.
Вот и делим обе части нашего соотношения на «пи» и получаем один радиан в градусах:
Это приближённое равенство также очень полезно запомнить. В одном радиане примерно 60 градусов. Такой грубой оценки бывает вполне достаточно для ответа на очень многие каверзные вопросы, связанные с углами. Бывает и недостаточно, конечно. В своё время мы такие хитрые задачки рассмотрим.)
Но это не самое главное применение этой формулы!) А самое главное — перевод радианов в градусы и обратно.
Переводим радианы в градусы!
Чаще всего углы в тригонометрии заданы в радианах с числом «пи». Это — самая стандартная ситуация. Если угол задан в радианах с числом «пи», то всё очень просто. Мы знаем, что «пи» радиан — это 180 градусов. Вот и подставляем вместо «пи» радиан — число 180. Сокращаем всё что сокращается и получаем угол в градусах.
Или более мудрёный угол:
Переводим градусы в радианы!
Обратный перевод градусов в радианы чуть сложнее, но ненамного. Если угол задан в градусах, то сначала нам надо узнать, сколько составляет один градус в радианах. И умножить это значение на количество градусов.) И чему же равен 1° в радианах?
Вот и все дела. Умножаем дробь π /180 на количество градусов, сокращаем что сокращается и получаем угол в радианах. Например:
Вот и всё. Заменять «пи» на примерно 3,14 никакой необходимости нет: его всегда буквой пишут. Что правда, то правда: нас же в заданиях обычно точный ответ интересует! А не приближённый.) Кстати, кому интересен приближённый ответ, посчитайте на калькуляторе. Получите примерно 0,628 и 2,356 радиана соответственно.
Итак, в непринуждённой беседе с лирическими отступлениями мы узнали, что радианы — это очень даже просто, не больно и не страшно.) Да и перевод туда-обратно несложен. И «пи» — не кусается… Так откуда же проблемы?
Это и приводит к казусам. Человек смотрит на пример, видит «пи» и автоматически считает, что это 180°. Везде и всюду. Кстати, это срабатывает. До поры до времени, пока примеры — типовые. Но любое отклонение примера от шаблона — тут же валит наповал! Почему?
Потому, что само по себе «пи» — это число! А никакие не градусы! Это «пи» радиан = 180°!
Ещё раз запоминаем:
Это заклинание надо понимать железно. Причём не просто механически зазубрить, а именно понимать каждое слово и каждый значок! И особенно — слово «радиан». Я не шучу. Ибо, если на вопрос, «Что такое «пи» в тригонометрии?», вы, блистая знаниями, радостно заявляете:
то это говорит о том, что вы не понимаете до конца смысла этой зелёной фразы. И все дальнейшие беседы уже бессмысленны, да…
Ещё раз: «пи» — это число! Примерно равное 3,14. Точного значения этого числа не знает никто: оно бесконечно длинное, корявое, иррациональное. Но — число! Такое же, как 2 или 7. Можно пройти примерно «пи» километров. Три километра и ещё около 140 метров. Можно купить «пи» килограммов картошки. Если продавец образованный встретится.) Можно выпить «пи» литров кока-колы. Если здоровье не жалко… И так далее…
Всё равно непонятна зелёная запись? Хорошо, вот вам простые житейские фразы:
1 километр — это 1000 метров;
3 часа — это 180 минут;
2 года — это 730 дней;
И тому подобное. Точно так же и с градусами/радианами:
«Пи» радиан — это 180 градусов!
Уяснили, что «пи» — это просто число? Или я уже достал вас этой заезженной фразой? Ну ладно, убедили. Тогда вот вам парочка нестандартных вопросов:
А теперь сравниваем эти два синуса. Как? По кругу, разумеется! Рисовать углы мы с вами уже умеем, что такое синус угла на круге — тоже знаем. Вперёд! Рисуем круг, углы примерно 0,79 ° и 45° и смотрим какие синусы у этих углов. Даже на самом корявом круге будет видно, что sin45° гораздо больше, чем sin0,79°.
С косинусами — всё то же самое. Рисуем на круге в правильных четвертях углы примерно 5 градусов и 5 радианов (помним, чему примерно равен один радиан в градусах?). Круг нам всё и подскажет. А именно, что cos5 меньше, чем cos5°.
Вообще, задачки с углами в радианах без «пи» (типа определить знак выражения sin10∙cos20) относятся к разряду нестандартных. В следующем уроке разберём парочку таких.)
Ну что, потренируемся с переводом углов?) Решаем несложные задания.
1. Переведите следующие углы из градусной меры в радианную:
Ответы (по возрастанию):
Как вы думаете, что это были за углы? Да! Это углы, которые попадают на координатные оси! Эти опорные значения надо держать в голове надёжно. До автоматизма! Как в градусах, так и в радианах. Зачем? Да всё за тем же! Для правильного распределения любых углов по четвертям.) Это полезное умение — залог успеха в любом задании по тригонометрии. Любом! От примитивных примеров до вполне себе солидных ЕГЭшных задачек части 2 (уравнения с отбором корней, тригонометрические неравенства и прочие хитрые штучки).
2. Переведите углы в радианную меру:
Ответы (в беспорядке):
Переведите следующие углы из радианной меры в градусную:
Ответы (в беспорядке):
300°; 225°; 120°; 330°; 240°; 135°; 210°; 315°; 150°.
А это что за углы? Правильно! Это углы, в пределах одного оборота, кратные предыдущим трём! Но не попадающие на оси координат. Такие углы вы также обязаны уметь просчитывать! И более того, все углы, кратные 30, 45 или 60 градусам, вы обязаны уметь просчитывать! Как в пределах одного оборота, так и за его пределами. Как положительные, так и отрицательные… В соответствующем уроке мы научимся с вами проделывать такие полезные вещи.
Если и это получилось, то тогда можно считать, что перевод радианов в градусы и обратно — уже не ваша проблема. Но перевод углов из одной размерности в другую — это лишь ещё один шаг вперёд к успешному постижению тригонометрии. Шаг мощный, но недостаточный. Ведь, чаще всего, с углами надо потом ещё и что-то делать.) Рисовать на круге, например. Или синус/косинус считать. Да и тангенс/котангенс тоже…
Второй серьёзный шаг — это умение правильно определять положение любого угла на тригонометрическом круге. Любого! Как в градусах, так и в радианах. С градусами на круге мы уже плотно поработали в предыдущем уроке. Теперь настал черёд набивать руку в работе с радианами.