Что такое градиент скорости в жидкости

Градиент скорости

В вязкой жидкости существует перепад скоростей ее движущихся слоев вдоль оси Z, перпендикулярнойнаправлению движения жидкости.

Количественно величина различий в скорости движения слоев жидкости характеризуется градиентомскорости dv/dx, называемым также скоростью сдвига.

Значение градиента скорости жидкости, текущей по трубе, так же как и величина скорости, изменяется отстенок к центру. Однако,если скорость минимальна у стенок и максимальна в центре, то значениеградиента, наоборот, максимально у стенок и минимально вблизи центра.

В 1851 Джордж Стокс получил выражение для силы трения (также называемой силой лобового сопротивления), действующей на сферические объекты с очень маленькими числами Рейнольдса (например, очень маленькие частицы) в непрерывной вязкой жидкости, решая уравнение Навье — Стокса:

· — сила трения, так же называемая силой Стокса,

· — радиус сферического объекта,

· — динамическая вязкость жидкости,

· — скорость частицы.

Если частицы падают в вязкой жидкости под действием собственного веса, то установившаяся скорость достигается, когда эта сила трения совместно с силой Архимеда точно уравновешиваются силой гравитации. Хотя в классической формулировке закон Архимеда выполняется только в статическом случае, а не для движущихся тел, в данном случае выражение для силы Архимеда сохраняет традиционный вид. Результирующая скорость равна

· V_s — установившаяся скорость частицы (м/с) (частица движется вниз если , и вверх в случае ),

· — радиус Стокса частицы (м),

· g — ускорение свободного падения (м/с²),

· — динамическая вязкость жидкости (Па с).

Закон Архимеда формулируется следующим образом [1] : на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме тела. Сила называется силой Архимеда:

где — плотность жидкости (газа), — ускорение свободного падения, а — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена кцентру тяжести этого объёма.

Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.

Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.

Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.

Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела.

где P_A, P_B — давления в точках A и B, ρ — плотность жидкости, h — разница уровней между точками A и B, S — площадь горизонтального поперечного сечения тела, V — объём погружённой части тела.

В теоретической физике также применяют закон Архимеда в интегральной форме:

,

где — площадь поверхности, — давление в произвольной точке, интегрирование производится по всей поверхности тела.

В отсутствие гравитационного поля, то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами.

На шарик, падающий в исследуемой жидкости, действуют три силы: сила тяжести, подъемная сила и сила сопротивления.
Если шарик медленно падает в безграничной среде, не оставляя за собой завихрений, то, как показал Стокс, сила сопротивления равна:
,
где — коэффициент внутреннего трения,
— скорость шарика,
— его радиус.

Дата добавления: 2014-12-20 ; просмотров: 18 | Нарушение авторских прав

Источник

Градиент скорости

Градиент скорости

В вязкой жидкости существует перепад скоростей ее движущихся слоев вдоль оси Z, перпендикулярной направлению движения жидкости.

Количественно величина различий в скорости движения слоев жидкости характеризуется градиентом скорости dv/dx, называемым также скоростью сдвига.

Значение градиента скорости жидкости, текущей по трубе, так же как и величина скорости, изменяется от стенок к центру. Однако,если скорость минимальна у стенок и максимальна в центре, то значение градиента, наоборот, максимально у стенок и минимально вблизи центра.

Смотреть что такое «Градиент скорости» в других словарях:

градиент скорости — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN velocity gradient … Справочник технического переводчика

градиент скорости тектонических движений — 3.27 градиент скорости тектонических движений: Изменение амплитуды тектонического перемещения маркирующей поверхности на единице расстояния в единицу времени. Источник … Словарь-справочник терминов нормативно-технической документации

боковой градиент скорости (сейсм.) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN lateral velocity gradient … Справочник технического переводчика

вертикальный градиент скорости (сейсм.) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN velocity depth gradientvertical velocity gradient … Справочник технического переводчика

горизонтальный градиент скорости (сейсм.) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN horizontal velocity gradientvelocity distance gradient … Справочник технического переводчика

региональный градиент скорости (сейсм.) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN regional velocity gradient … Справочник технического переводчика

ВЕРТИКАЛЬНЫЙ ГРАДИЕНТ СКОРОСТИ ВЕТРА — 1. Градиент модуля скорости ветра (скалярный), представляющий собой разность модулей скорости ветра на двух соседних уровнях (скорость вверху минус скорость внизу выбранного слоя), отнесенную к единичному слою атмосферы. 2. Векторный В. г. с. в … Словарь ветров

Градиент — 12 Градиент DР/е Перепад давления, деленный на толщину образца Источник: ГОСТ 25283 93: Материалы спеченные проницаемые. Определение проницаемости жидкостей … Словарь-справочник терминов нормативно-технической документации

Градиент ветра — Перистые когтевидные облака, формирующиеся в зонах значительного градиента ветра. Градиент ветра градиент скорости и направления ветра в случаях, когда они значительно изменяются на относительно небольшом участке в атмос … Википедия

Градиент (вектор) — Градиент (от лат. gradiens, род. падеж gradientis шагающий), вектор, показывающий направление наискорейшего изменения некоторой величины, значение которой меняется от одной точки пространства к другой (см. Поля теория). Если величина выражается… … Большая советская энциклопедия

Источник

Градиент скорости это физика

В вязкой жидкости существует перепад скоростей ее движущихся слоев вдоль оси Z, перпендикулярной направлению движения жидкости.

Количественно величина различий в скорости движения слоев жидкости характеризуется градиентом скорости dv/dx, называемым также скоростью сдвига.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10072 – | 7513 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

градиент скорости — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN velocity gradient … Справочник технического переводчика

градиент скорости тектонических движений — 3.27 градиент скорости тектонических движений: Изменение амплитуды тектонического перемещения маркирующей поверхности на единице расстояния в единицу времени. Источник … Словарь-справочник терминов нормативно-технической документации

боковой градиент скорости (сейсм.) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN lateral velocity gradient … Справочник технического переводчика

вертикальный градиент скорости (сейсм.) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN velocity depth gradientvertical velocity gradient … Справочник технического переводчика

горизонтальный градиент скорости (сейсм.) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN horizontal velocity gradientvelocity distance gradient … Справочник технического переводчика

региональный градиент скорости (сейсм.) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN regional velocity gradient … Справочник технического переводчика

ВЕРТИКАЛЬНЫЙ ГРАДИЕНТ СКОРОСТИ ВЕТРА — 1. Градиент модуля скорости ветра (скалярный), представляющий собой разность модулей скорости ветра на двух соседних уровнях (скорость вверху минус скорость внизу выбранного слоя), отнесенную к единичному слою атмосферы. 2. Векторный В. г. с. в … Словарь ветров

Градиент — 12 Градиент DР/е Перепад давления, деленный на толщину образца Источник: ГОСТ 25283 93: Материалы спеченные проницаемые. Определение проницаемости жидкостей … Словарь-справочник терминов нормативно-технической документации

Градиент ветра — Перистые когтевидные облака, формирующиеся в зонах значительного градиента ветра. Градиент ветра градиент скорости и направления ветра в случаях, когда они значительно изменяются на относительно небольшом участке в атмос … Википедия

Градиент (вектор) — Градиент (от лат. gradiens, род. падеж gradientis шагающий), вектор, показывающий направление наискорейшего изменения некоторой величины, значение которой меняется от одной точки пространства к другой (см. Поля теория). Если величина выражается… … Большая советская энциклопедия

Градиентом любой физической величины называется изме­нение этой величины, отнесён­ное к расстоянию, вдоль которого это изменение происходит.

3. Силы внутреннего трения зависят от при­роды жидкости, так как молекулы различных жидкостей находятся на различных расстояниях и имеют различную скорость, а следовательно и ки­нетическую энергию. Эта зависимость учиты­вается коэффициен­том вязкости – η. Таким образом, силы внутреннего трения зави­сят от природы жидкости, прямо пропорциональны градиенту скорости и площади соприкасаю­щихся слоев.

Эта формула получила название формулы Ньютона. Если пло­щадь соприкасающихся слоев S = 1 и градиент скорости dυ/dx = 1, то Fтр = η

Коэффициентом вязкости или вязкостью жидкости назы­вается величина численно равная силе трения, возникающей между двумя слоями жидкости, соприкасающимися на площа­ди равной единице и при градиенте скорости между ними рав­ным единице.

Коэффициент вязкости измеряется в системе СИ: η =Fηdx/Sdυ; Н м / м 2 (м/с) = Н с / м 2 = Па с

В системе СГС: Пуаз (Пз) = дн с / см 2 ; Н с / м 2 = 10 5 дн с / 10 4 см 2 = 10 Пз. В медицине принято измерять вязкость в Пуазах. Коэффициент вязкости зависит не только от природы жидко­сти, но и от температуры. С повышением темпе­ратуры коэффи­циент вязкости уменьшается. Это объясняется тем, что с повыше­нием температуры расстояния между молекулами увеличивают­ся, а силы взаимодействия ослабляются.

Ввиду больших трудностей, возникающих при непосредствен­ном измерении вязкости её определяют косвенным путём. Наи­большее применение имеют методы: падающего шарика и капил­лярного визкозиметра. Метод падающего шарика основан на законе Стокса. Стокс устано­вил, что на небольшое тело шаровидной формы, перемещающееся в жидкости, действует сила трения, прямо про­порциональная радиусу этого тела, его скорости и коэффициенту вязкости жидкости.

Если бросить в жидкость металлический шарик диаметром 0,2—0,3 мм, то он будет двигаться в жидкости равномерно. На движу­щийся шарик будут действовать три силы

1. Сила тяжести Р = mg, направленная верти­кально вниз.

2. Выталкивающая сила FB, направленная вертикально вверх.

3. Сила трения FTp, направленная также верти­кально вверх.

По первому закону Ньютона тело двига­ется равномерно, если равнодействующая всех сил, действующих на него, равна 0.

Радиус шарика можно измерить с помощью микроскопа с окулярным микрометром, скорость движения шарика можно определить по формуле V = s /t, измерив линейкой s, а секундо­мером – t. Метод довольно точен, используется в санитарии. В медицинской практике для определения коэффициента вяз­кости крови, спиномозговой жидкости и других биологических жидкостей пользуются методом капиллярного вискозиметра, ос­нованный на законе Гагена-Пуазейля. Они установили, что объём жидкости, протекающей через попереч­ное сечение капилляра (R 4 , dP/dl и обратно пропорционален η, коэффициент пропорци­ональности в системе СИ равен π/8.

где dP/dl — градиент давления, dP — разность давлений в начале и в конце капилляра, dl — длина капилляра. При пропускании жидкостей через капилляры с одинаковым радиусом при одинаковом градиенте давления, получим:

Найдём относительную вязкость, поделив 1 выражение на 2.

Вискозиметр состоит из двух пипеток – капилля­ров, укреплённых на общей подставке. Один капилляр имеет кран. Сначала втягивая воздух заполняют капилляр (б) стандарт­ной жидкостью, как правило водой, до нулевого деления, закры­ва­ют кран и затем заполняют капилляр (а) исследуемой жидкостью до нулевого деления. Открыв кран, втягивают обе жидкости одно­временно так, чтобы исследуемая жидкость дошла до деления.

Тогда число делений трубки (б) укажет относи­тельную вякость. Зная η₁, определим η₂ по формуле:

Преимущество и недостатки этого метода:

2. Быстрота измерения (особенно для крови — быстро свёр­тывается);

3. Измерение вязкости непрозрачных жидкостей.

Недостаток — малая точность ввиду отсутствия стандарта. Течение жидкости называется лами­нарным или слоистым, если поток жидкости представляет собой совокупность слоев, пе­ремещающихся относительно друг друга без перемешивания. При некоторой высокой скоро­сти течение становится турбулентным (вихре­вым), когда происходит перемешивание слоев жидкости. При турбулентном течении жидкости возрастают силы трения, а следовательно и работа по преодолению сил трения. Это тече­ние жидкости сопровождается звуковым феноменом.

Скорость, при которой ламинарное течение переходит в турбулентное называется критической (υ кр.)

Величина этой скорости зависит от вязкости жидкости, радиуса трубки, плотности жидкости и состояния внутренней поверхности. Критическая скорость вычисляется по формуле:

где η – вязкость жидкости, р – плотность, D – диаметр трубки. Безразмерная величина R_се называется числом Рейнольдса. Для гладких трубок R_се = 2300, для трубок с шероховатыми поверхнос­тями эта величина меньше.

Источник

4.1 Вязкость жидкостей и вискозиметрия как метод характеристики коллоидных систем и растворов полимеров
4.1.1. Вязкость жидкостей

Вязкой называют жидкость, в которой между отдельными частицами (молекулами) существуют такие силы притяжения, которые при перемещении одной части жидкости относительно другой сдерживают движение слоев. Очевидно, что все жидкости должны быть вязкими, так как между реальными молекулами всегда существуют силы не только притяжения, но и отталкивания. Равновесие между этими силами и обусловливает равновесное состояние жидкости. Если один из слоев жидкости вывести из состояния равновесия и перемещать его с некоторой скоростью относительно другого, то силы притяжения частиц будут тормозить это движение.

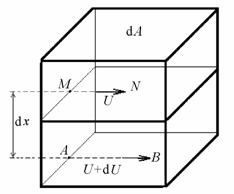
При теоретическом описании вязкости жидкость рассматри­вают как непрерывную бесструктурную среду. В равновесном состоянии частицы (молекулы) будут располагаться таким образом, что равновесная сила (разность между силами притяжения и отталкивания) равна нулю. Если это не соблюдается, то молекулы будут перемещаться относительно друг друга до тех пор, пока вновь не наступит состояние равновесия. Если под действием какой-либо силы жидкость привести в движение (как показано на рис. 2.26) таким образом, что один из слоев, например АB, будет перемещаться с ускорением dU по отношению к слою MN, то между слоями возникнет сила трения, стремящаяся выравнять скорости движения слоев АВ и MN и вернуть их в состояние равновесия. Можно ожидать, что сила трения F_f прямо пропорциональна относительной скорости движения dU и площади контакта слоев dA и обратно пропорциональна расстоянию между слоями dx (между центрами движущихся слоев).

где Р– напряжение течения, h– коэффициент пропорциональности, называемый коэффициентом вязкости или вязкостью,dU/dx– градиент скорости течения.

Рис. 2.26. Схема течения жидкости в капилляре. Площадь контакта слоев dA, расстояние между слоями dx

Уравнение (2.4.1) было получено Ньютоном в 1687 г. Вязкость при ламинарном течении является функцией исключительно сил межмолекулярного взаимодействия в жидкости, поэтому может служить характеристикой интенсивности этих сил и зависит от температуры.

По физическому смыслу вязкость соответствует силе (выраженной в ньютонах) при площади контакта слоев dA (1 м 2 ) и градиенте скорости (1 м/с) в системе СИ имеет размерность h = [Па×с]. В честь ученого Пуазейля, который посвятил много работ изучению вязкости и предложил метод ее измерения, часто используется единица, называемая «пуаз» 1П = 0,1 Па×с. Жидкости, подчиняющиеся при течении закону Ньютона называют ньютоновскими, или нормальными.

Из уравнения (2.4.1) вытекают два следствия:

1. При течении жидкости вдоль неподвижной стенки, прилегающий к ней, слой должен иметь наименьшую скорость течения, так как молекулы жидкости притягиваются к твердой поверхности. По мере удаления слоев жидкости от твердой стенки скорость течения будет увеличиваться. Максимальная скорость будет у слоя жидкости, наиболее удаленного от твердой стенки. Поэтому при течении жидкости в ее объеме повсюду имеется градиент скорости. Во всем объеме жидкости коэффициент вязкости будет одинаковым и лишь при перемещении слоя, прилегающего непосредственно к твердой стенке, коэффициент трения будет характеризовать межмолекулярное взаимодействие молекул жидкости и твердого тела, из которого сделана стенка. Эта сила при достаточном объеме жидкости обычно пренебрежимо мала.

2. Если рассматривать не движение жидкости относительно неподвижной стенки, а движение твердой частицы через стационарную жидкость, то картина будет такой: слой жидкости, прилегающей непосредственно к твердой частице, будет перемещаться с той же скоростью, что и частица. По мере удаления от поверхности частицы слои жидкости будут перемещаться со все меньшей скоростью. Жидкость должна двигаться вместе с частицей и общая сила трения будет складываться в основном из сил трения слоев жидкости друг о друга, а силой трения жидкости о частицу можно пренебречь.

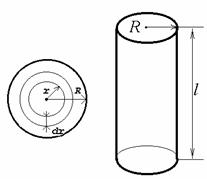
Рис. 2.27. Схема капилляра, использован­ная при выводе уравнения Пуазейля

Рассмотрим элемент объема, заключенный между концентрическими цилиндрами, как показано на рис. 2.27. Радиусы цилиндров различаются на малую величину dr. Один цилиндр отстоит от центра капилляра на расстояние r, а другой r+dr. Элемент объема проходит вдоль всего капилляра длиной l. При ламинарном (пластинчатом) режиме течения этот элемент объема жидкости в капилляре не смешивается с другими. Площадь его соприкосно­вения с внутренним элементом объема составляет 2rl, а с наружным 2l(r+dr). Жидкость во внешнем элементе объема движется медленнее, а во внутреннем – быстрее выделенного нами элемента. Поэтому на условно выделенный нами объем действуют две силы: одна (со стороны внутреннего элемента) ускоряет движение, а другая (со стороны внешнего элемента объема) замедляет.

В стационарном режиме течения эти противоположные по направлению силы будут равны по величине и представляют собой произведение давления на элемент площади, т.е. Р(2prdr).

Сила трения задается уравнением (2.4.1).

(2.4.2)

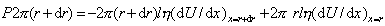
Знак «минус» в правой части уравнения объясняется тем, что по внешней поверхности элемента жидкости движение будет затормаживаться, а «плюс» – тем, что по внутренней его поверхности движение ускоряется.

Разлагая в ряд Тэйлора правую часть уравнения (2.4.2) и учитывая, что dU/dx (при х=r+dr) равно dU/dx (при x=r) плюс (d 2 U/dr 2 )dr, и деля каждую часть уравнения (2.4.2) на 2p dr, получаем

гдеdU/dr– градиент скорости на расстоянии r от центра капилляра.

Первое интегрирование дает

где А₁ – постоянная интегрирования.

Второе интегрирование приводит к уравнению зависимости линейной скорости течения слоя жидкости от расстояния до центра капилляра

где А₂ – постоянная второго интегрирования.

Постоянная А₁ =0, что следует из уравнения (2.4.4) при условии, что r=0. Физический смысл постоянной А₂вытекает из уравнения (2.4.5) при условии, что при r=R U=0.

U = P(R 2 – r 2 )/(4lh). (2.4.7)

Это уравнение дает параболическое распределение скоростей течения жидкости в зависимости от расстояния до центра капилляра.

Более удобной для практического использования является объемная скорость течения, т.е. объем жидкости, протекающей через капилляр с радиусом поперечного течения r за одну секунду. Объем протекающей жидкости будет разным для каждого из элементов объема капилляра, зависит от линейной скорости U и будет равен произведению U на площадь поперечного сечения элемента объема:

Общий объем жидкости, протекающей за одну секунду получают интегрированием по всем элементам объема:

Уравнение (2.4.9) известно как уравнение Пуазейля. Его часто записывают в форме

, (2.4.10)

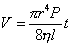
где V – объем жидкости, вытекающей через капилляр длиной l и радиусом r за время t (с) под давлением Р.

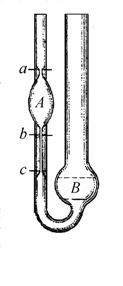
Уравнение Пуазейля используют при определении вязкости с помощью капиллярных вискозиметров. Пример наиболее популярного капиллярного вискозиметра Оствальда-Пинкевича приведен на рис. 2.28. Здесь a и b– метки, ограничивающие объем А; bс– длина капилляра; В –сосуд.

Если жидкость вытекает под действием собственной тяжести, то в капиллярных вискозиметрах фиксируется начальный h₁ и конечный h₂ уровень жидкости за промежуток времени от 0 до t. В капиллярных вискозиметрах давление Р в процессе течения не остается постоянным, изменяясь от Р₀ = rgh₁ до Р_t = rgh₂, где r– плотность жидкости; g– ускорение свободного падения.

. (2.4.11)

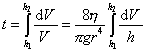
Интеграл в правой части уравнения (2.4.11) представляет собой постоянную вискозиметра, также как r и l. Объединяя все постоянные в одну, можем получить для каждого капиллярного вискозиметра

Отношение h/r называют кинематической вязкостью. Постоянная вискозиметра определяется путем измерения времени истечения между метками на капилляре жидкости с известными значениями h и r.

Если скорость истечения жидкости из капилляра велика (т.е. мало время истечения), то необходимо учитывать поправку на разность кинетической энергии жидкости, входящей в капилляр и вытекающей из нее, так как часть давления DР=grDh приходится на ускорение жидкости.

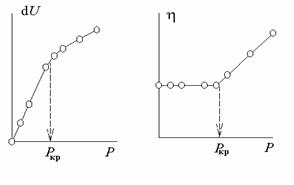
Градиент скорости (или скорость) течения ньютоновских жидкостей линейно растет при повышении давления, приводящего жидкость в движение, до того критического значения Р_кр, когда режим течения из ламинарного переходит в турбулентное.

Вязкость этих жидкостей не зависит от давления вплоть до той же величины Р_кр. При турбулентном режиме течения h теряет свой смысл. Схема зависимости вязкости и градиента скорости от давления показана на рис. 2.29.

Рис. 2.29. Зависимость градиента скорости течения и вязкости ньютоновской жидкости от напряжения (схема)

Источник