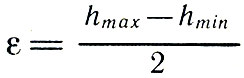Что такое горизонтальные координаты

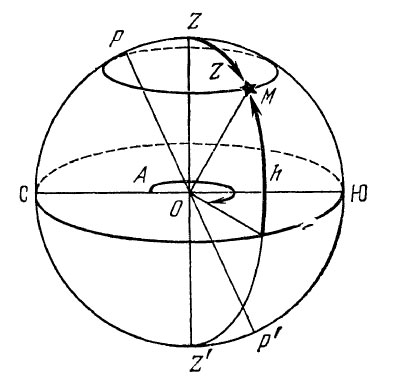
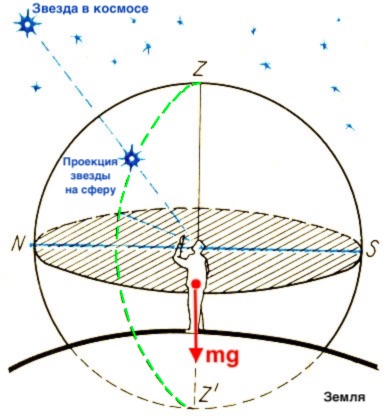
Рис. 6. Горизонтальная система координат

Горизонтальная система координат

В горизонтальной системе координат основной плоскостью является плоскость истинного горизонта местности, а полюсами — зенит и надир.
Плоскости, содержащие линию «зенит – надир» и потому проходящие через центр небесной сферы, называются вертикалами. Вертикал, проходящий через точки востока и запада, и тем самым перпендикулярный плоскости небесного меридиана, называется первым вертикалом.
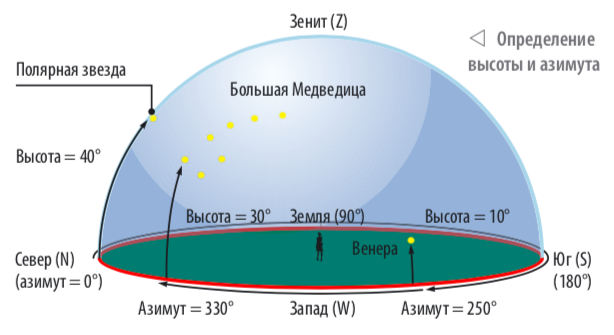
Определяющими параметрами в горизонтальной системе координат являются азимут и высота небесного объекта над горизонтом.
Высота (h) отсчитывается от плоскости горизонта: в видимой небесной полусфере со знаком «плюс», а в невидимой небесной полусфере — со знаком «минус». Как и географическая широта, аналогом которой она в какой-то мере является, высота измеряется в пределах от +90° до –90°.
Вместо высоты h иногда используют зенитное расстояние z, величина которого определяется соотношением: z = 90° – h. Геометрически зенитное расстояние представляет собой угол между направлением на точку зенита (вертикальной осью) и направлением на небесный объект. Величина z всегда положительна и может принимать значение в пределах от 0° (в точке зенита) до 180° (в точке надира).
Азимут (А) представляет собой двугранный угол между плоскостью нулевого небесного меридиана и плоскостью вертикала и аналогичен географической долготе. Азимут отсчитывается от направления на юг по ходу часовой стрелки и измеряется в пределах от 0° до 360°.

Источник

Горизонтальная система небесных координат в навигации

Принципы горизонтальной системы небесных координат и примеры навигационных расчетов.

Горизонтальная система небесных координат – навигационная система для авиационного и морского транспорта, в которой положение светила на небесной сфере ориентируют относительно истинного горизонта. Если проще, то в горизонтальной системе небесных координат за основную плоскость принимается плоскость истинного горизонта, а полюсами, соответственно, являются зенит и надир (самая верхняя и с самая нижняя точки) небесной сферы.

Положение светила в горизонтальной системе координат определяется азимутом и высотой светила.

Общая схема принципа действия горизонтальной системы небесных координат

Принцип горизонтальной системы небесных координат

Азимутом светила А называется двугранный угол в плоскости истинного горизонта, заключенный между плоскостью небесного меридиана и плоскостью вертикала светила. Азимут отсчитывается от северного направления небесного меридиана по ходу часовой стрелки от 0 до 360°. Светила, находящиеся на одном вертикале, имеют одинаковые азимуты.

Положение светила на вертикале определяется другой координатой —высотой. Высотой светила h называется угол между плоскостью истинного горизонта и направлением на светило из центра небесной сферы. Высоту можно измерять также дугой вертикала от плоскости истинного горизонта до альмукантарата светила. Высота измеряется от 0 до ±90°.
Положительные высоты светила отсчитываются к зениту, а отрицательные к надиру, т. е. светила, находящиеся над горизонтом, имеют положительную высоту, а находящиеся под горизонтом — отрицательную. Вместо высоты светила иногда пользуются другой координатой — зенитным расстоянием.

Зенитным расстоянием Z называется угол в плоскости вертикала, заключенный между вертикалью наблюдателя и направлением на светило из центра небесной сферы. Зенитное расстояние отсчитывается от точки зенита до направления на светило от 0 до 180°.

Между высотой и зенитным расстоянием светила существует следующая зависимость:

h+Z = 90°, откуда Z = 90° — h; h = 90° — Z.

Светила, находящиеся на одном альмукантарате, имеют одинаковые высоты и одинаковые зенитные расстояния.

Особенности горизонтальной системы небесных координат

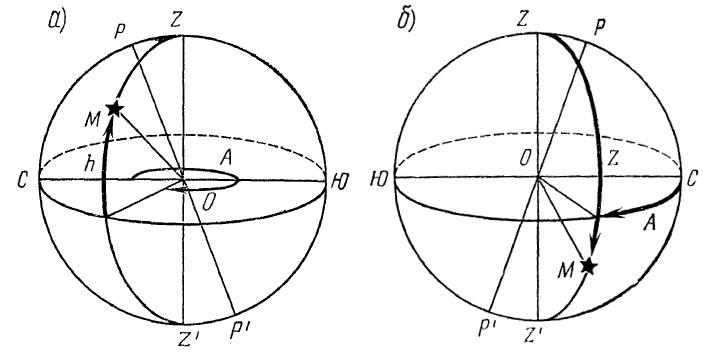
Горизонтальные координаты светил непрерывно и неравномерно изменяются вследствие суточного вращения Земли. Они изменяются также и с переменой места наблюдателя. Однако горизонтальные координаты удобны тем, что их можно непосредственно измерить с помощью специальных приборов и по ним легко можно представить положение светила на небесной сфере. Ниже приведены примеры графического изображения положения светил на небесной сфере по за-данным горизонтальным координатам.

Иллюстрация принципа определения координат объекта с помощью горизонтальной системы небесных координат (к примерам 1 и 2 выше)

источник: по книге “Авиационная астрономия”

Источник

Горизонтальная система координат

Рис. 14. Горизонтальная систе­ма координат

За основу в горизонтальной системе координат при­нята вертикальная линия ZZ (рис. 14). Основной большой круг — математический горизонт (слово «математический» можно опустить).

Для измерения координат проводится большой круг (круг высот) от зенита Z через светило (Σ) до надира Z’. Координа­той служит высота (h), измеряемая от горизонта дугой круга склонений до светила (или соответствующим центральным уг­лом). Часто употребляется зенитное расстояние z, равное ду­ге того же круга от зенита до светила. Очевидно, что z+h = 90°.

Другой координатой служит азимут — дуга горизонта (или соответствующий угол), отсчитываемая от точки юга по на­правлению к западу.

Горизонтальная система координат жёстко связана с на­блюдателем. Для каждого наблюдателя существует своя гори­зонтальная система координат.

Переход к экваториальной системе

Поскольку координаты в горизонтальной системе координат показывают, в ка­кой части видимой полусферы неба можно найти интересующее светило, а экваториальная система позволит определить его положение на небесной сфере, нужно уметь перехо­дить от одной системы к другой. Очевидно, что для такого пе­рехода требуется прежде всего сориентировать одну систему координат относительно другой. Для этого нужно сориен­тировать сначала полярную ось относительно вертикали, за­тем найти поворот вращающейся небесной сферы относитель­но меридиана. Но в первую очередь необходимо сориентировать ось мира.

Высота полюса над горизонтом

На рисунке 16 изображено сечение Зем­ли плоскостью географического меридиана, проведённого в ме­сте наблюдения. Эта плоскость всегда совпадает с плоскостью небесного меридиана того же места. Наблюдатель находится в точке O. Материал с сайта http://wikiwhat.ru

Угол между плоскостью экватора и радиусом, проведённым к точке O, есть широта места наблюдения (φ). Угол h_p назы­вается высотой полюса над горизонтом. Очевидно, что эти уг­лы равны (как углы со взаимно перпендикулярными сторона­ми). Если определить высоту Полярной звезды над горизон­том, то, поскольку эта звезда (она же α Малой Медведицы) находится вблизи Полюса мира, можно оценить широту мес­та наблюдения. Это не самый точный способ, имеются и другие.

Зная широту места наблюдения, можно правильно ори­ентировать небесную сферу относительно наблюдателя, что поз­воляет решать задачи о видимости или невидимости звёзд, вре­мени их восхода и захода, продолжительности дня и ночи и т. д.

Источник

Небесные координаты

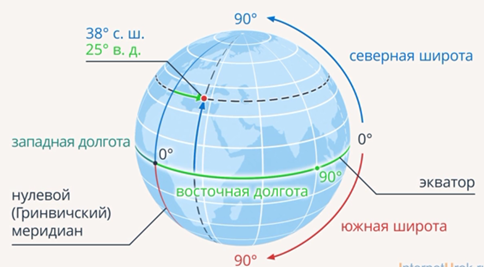
Чтобы лучше понять небесные координаты, сначала вспомним как мы определяем координаты своего положения на земле:

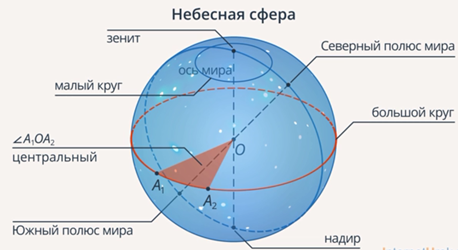
Теперь выделим важнейшие круги на небесной сфере:

Рис. 1. Небесная сфера, наблюдатель и Земля

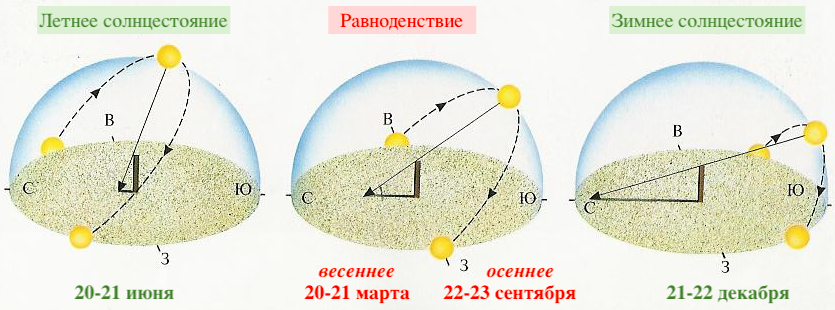
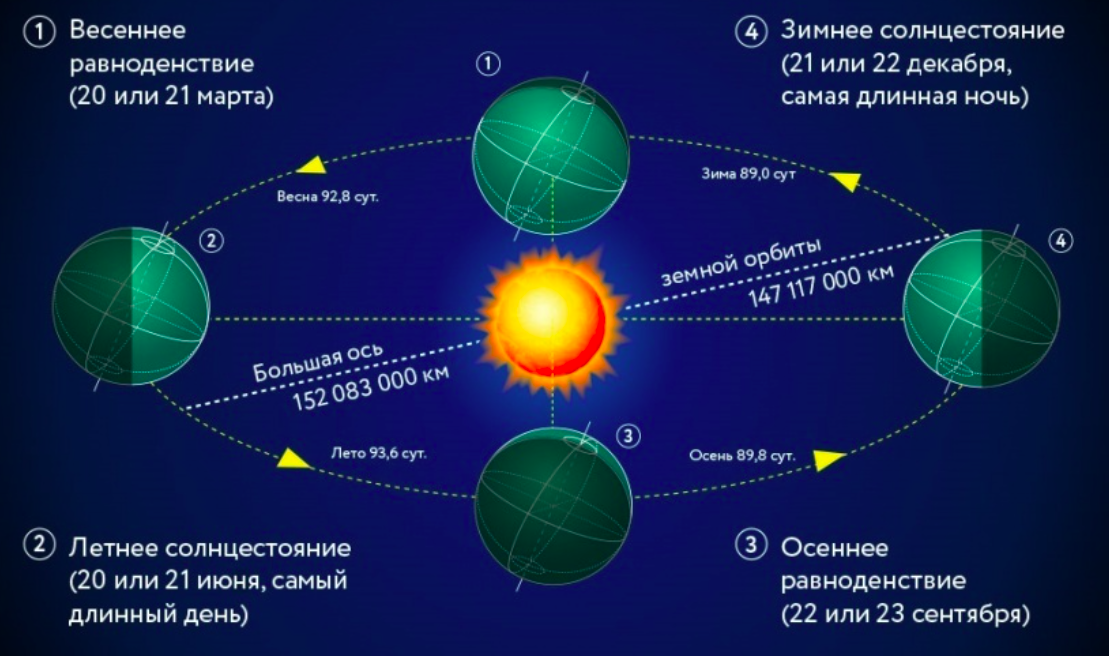
Равноденствие — это астрономическое явление, когда центр Солнца в своём видимом движении по эклиптике пересекает небесный экватор.

Солнцестояние — это астрономическое событие, при котором Солнце над горизонтом в истинный полдень находится на максимальной (летнее солнцестояние) или минимальной высоте (зимнее солнцестояние). В эти дни высота почти не изменяется — Солнце словно «стоит на месте». В ходе солнцестояний Солнце достигает максимальной высоты склонения к северу или югу относительно экватора Земли.

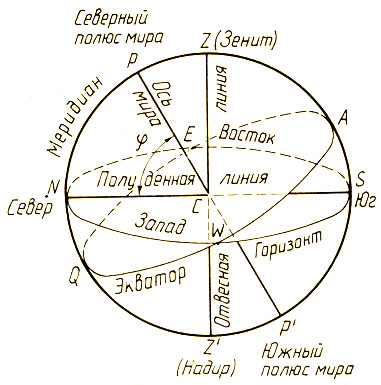
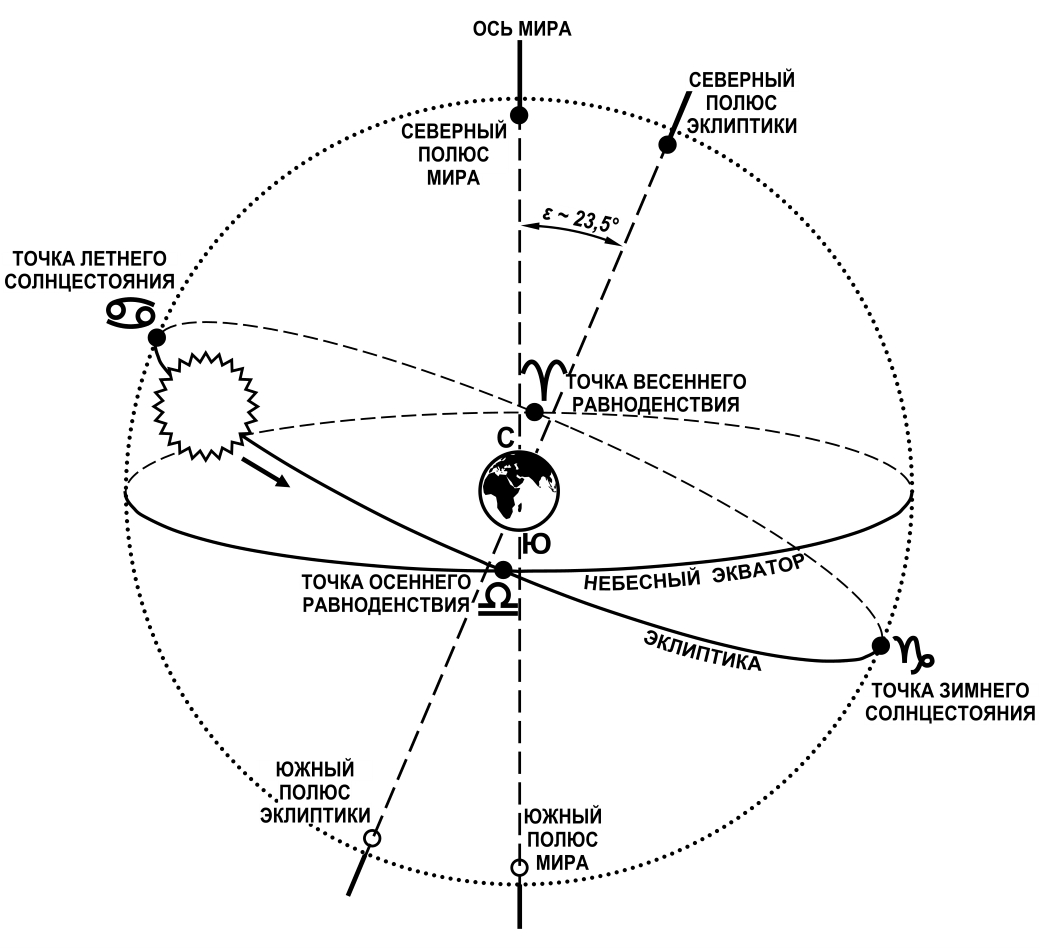
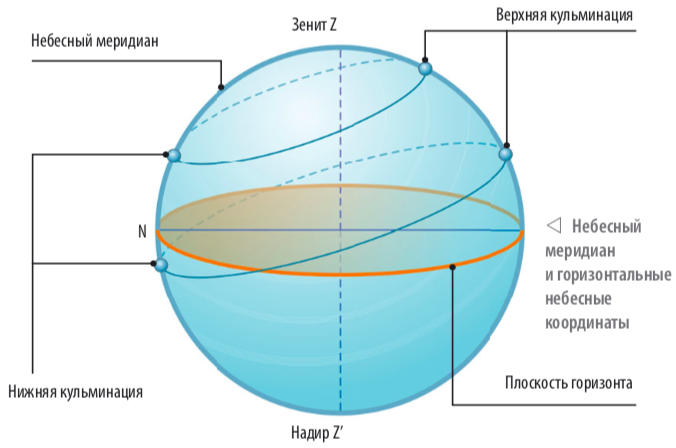
Рис. 2. Основные точки и линии небесной сферы

В китайских хрониках сообщается, что около 1100 г. до н. э. китайский астроном Чу Конг измерил наклон эклиптики к экватору и нашел его равным 23°54′. Как он это сделал? Двигаясь по эклиптике, Солнце все время меняет угловое расстояние от экватора. 22 июня, вдень летнего солнцестояния, Солнце находится в самой «верхней» точке эклиптики (точке летнего солнцестояния), т.е. в наибольшем удалении от экватора к северному полюсу мира. Пусть в этот день в полдень, когда Солнце находится над точкой юга, его угловая высота над горизонтом равна h_max. Через полгода, когда Солнце будет в точке зимнего солнцестояния, его полуденная высота пусть равна h_min. Нетрудно сообразить, что угол ε наклона эклиптики к экватору определится формулой

Что же касается полуденной высоты Солнца, то она определяется без всякого труда с помощью угломерных инструментов, которые изложены на данном сайте в разделе «Что и как изучает астрономия?» Величина ε имеет большое значение в астрономии. Она множество раз уточнялась разными астрономами и в настоящее время принимается равной 23°26′. Заметим, что на протяжении веков по ряду причин она слегка изменяется.

1. Горизонтальная система координат

Горизонтальная система небесных координат — это сферическая система координат, в которой основные точки — зенит и надир, основная плоскость — плоскость математического горизонта NWSE, а основные координаты — угловая высота и азимут (рис.3).

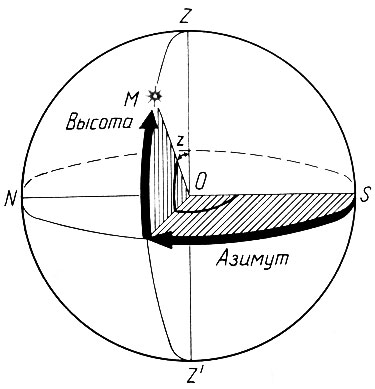
Рис. 3. Горизонтальные координаты

Значения азимута и высоты полностью определяют положение точки на небесной сфере. (В геодезии азимуты отсчитываются от точки севера к востоку). У небесных светил, кроме тех, которые находятся в полюсах мира, эти координаты все время меняются, что делает горизонтальную систему очень неудобной.

2. Экваториальная система координат

Экваториальная система небесных координат — это сферическая система координат, где основная плоскость — небесный экватор, основные точки — полюса мира, а координаты — склонение и прямое восхождение.

Экваториальные координаты очень удобны тем, что не зависят от вращения небесной сферы, поэтому сейчас получили наибольшее применение. Они очень похожи на географические координаты — широту и долготу. Роль широты играет склонение δ, а роль долготы — прямое восхождение (рис. 4).

Прямое восхождение — это длина дуги небесного экватора от точки весеннего равноденствия до круга склонения.

Склонение светила — это угловое расстояние светила от плоскости небесного экватора, измеренного вдоль круга склонения.

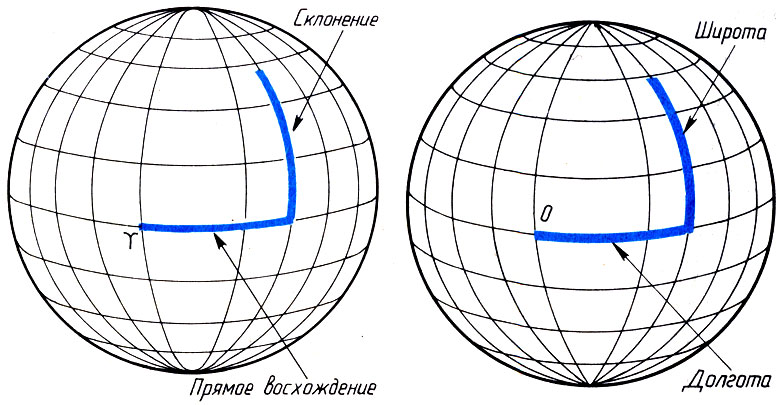
Рис. 4. Экваториальные (слева) и географические (справа) координаты

Склонение δ измеряется в градусах, причем считается положительным к северу от небесного экватора и отрицательным к югу от него. Прямое восхождение принято измерять в часах, минутах и секундах. При этом 360° соответствует 24 ч, откуда каждый час прямого восхождения соответствует 15°.

Построение небесной сферы будет неполным, если не уточнить, от чего зависит угол наклона оси мира к плоскости горизонта.

Около 320 г. до н. э. греческий астроном, географ и мореплаватель Питеас, убежденный в шарообразности Земли, впервые доказал, что угловая высота полюса мира над горизонтом всегда равна географической широте места.

Рассмотрите внимательно рис. 5. Так как видимое суточное вращение небосвода вызвано действительным вращением Земли вокруг оси, то ось мира, проведенная в данном пункте наблюдения, параллельна земной оси. Но тогда географическая широта места φ и угловая высота полюса мира над горизонтом h_p есть углы со взаимно перпендикулярными сторонами, равенство которых доказывается в элементарной геометрии.

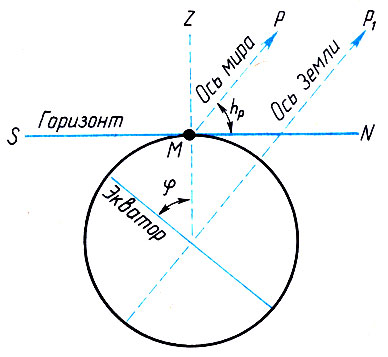
Рис. 5. Теорема о высоте полюса мира

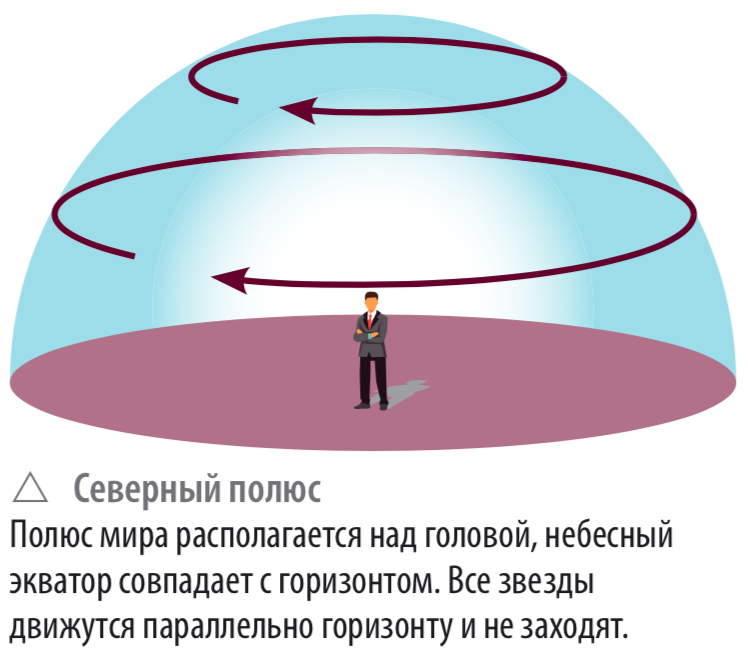
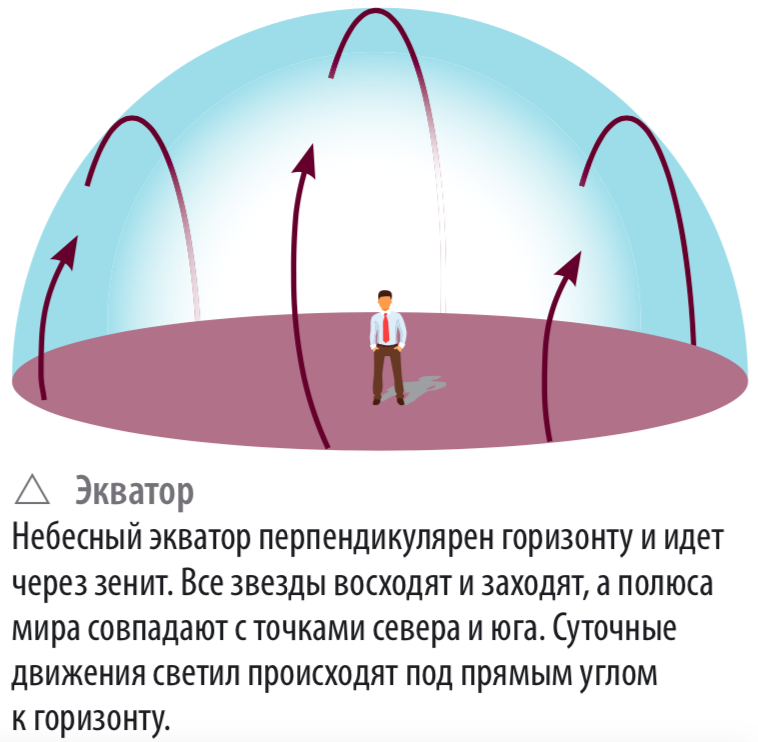
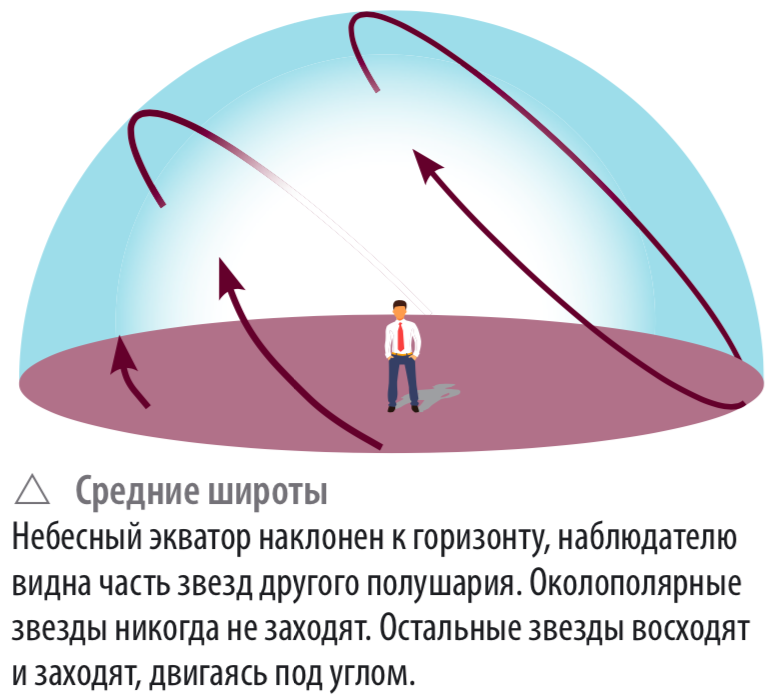
Для Москвы φ = 56°, и на московском небе есть никогда не заходящие и никогда не восходящие звезды. На полюсах Земли (φ = ±90°) над горизонтом видно всегда какое-нибудь одно полушарие звездного неба, причем звезды движутся параллельно горизонту. На земном экваторе (φ = 0°) другая картина: ось мира лежит в плоскости горизонта, все звезды восходят и заходят, причем их видимые пути перпендикулярны горизонту.

Источник

Горизонтальные координаты

Содержание

Описание

Линии и плоскости

Координаты

В горизонтальной системе координат одной координатой является либо высота светила h, либо его зенитное расстояние z. Другой координатой является азимут A.

Зенитным расстоянием z светила называется дуга вертикала светила от зенита до светила. Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.

Особенности изменения координат небесных тел

За сутки звезда (а также в первом приближении — тело Солнечной системы) описывает круг, перпендикулярный оси мира (PP’), которая на широте φ наклонена к математическому горизонту на угол φ. Поэтому она будет двигаться параллельно математическому горизонту лишь при φ равном 90 градусов, то есть на Северном полюсе. Поэтому все звёзды, видимые там, будут незаходящими (в том числе и Солнце на протяжении полугода, см. долгота дня) а их высота h будет постоянной. На других широтах доступные для наблюдений в данное время года звёзды делятся на

Максимальная высота h звезды будет наблюдаться раз в день при одном из двух её прохождений через небесный меридиан — верхней кульминации, а минимальная — при втором из них — нижней кульминации. От нижней до верхней кульминации высота h звезды увеличивается, от верхней до нижней — уменьшается.

Переход к первой экваториальной

Первая формула получена. Теперь к тому же сферическому треугольнику применяем теорему синусов:

Вторая формула получена. Теперь применяем к нашему сферическому треугольнику формулу пяти элементов:

Третья формула получена. Итак, все три формулы получены из рассмотрения одного сферического треугольника.

Переход от первой экваториальной

Источник