Что такое геометрическое построение модуля
Модуль числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение модуля числа
Алгебра дает четкое определение модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.
Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».
Знак модуля: |a| = OA.
Разберем на примере:
Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.
Число 3 (длину отрезка OB) называют модулем числа −3.
Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).
Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.
Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.
Также можно опустить плюс и записать значение, как |4| = 4.
Записывайся на занятия по математике для учеников с 1 по 11 классы.
Свойства модуля числа
Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.
1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:
2. Модуль положительного числа равен самому числу.
3. Модуль отрицательного числа равен противоположному числу.
4. Модуль нуля равен нулю.
5. Противоположные числа имеют равные модули.
6. Модуль произведения равен произведению модулей этих чисел.
Геометрическая интерпретация модуля
Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.
Нарисуем числовую прямую и отобразим это на ней.
Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.
Решим уравнение: |х| = 5.
Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.
График функции
График функции равен y = |х|.
Для x > 0 имеем y = x.
Этот график можно использовать при решении уравнений и неравенств.
Корень из квадрата
Оно равно a при а > 0 и −а, при а
Модуль комплексного числа
Чему равен модуль числа в данном случае? Это арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа:
Свойства модуля комплексных чисел
Модуль рационального числа
Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.
Модуль рационального числа, примеры:
Модуль вещественных чисел
Модуль противоположного числа, нуля, отрицательного и положительного чисел
Закрепим свойства модуля числа, которые мы рассмотрели выше:
Графический метод решения задач с параметрами
Теперь вы узнали, что такое параметр, и увидели решение самых простых задач.
Но подождите — рано успокаиваться и говорить, что вы все знаете. Есть множество типов задач с параметрами и приемов их решения. Чтобы чувствовать себя уверенно, мало посмотреть решения трех незатейливых задач.
Вот список тем, которые стоит повторить:
1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».
Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому. Конечно, он не единственный. Но начинать лучше всего именно с него.
Мы разберем несколько самых простых задач, решаемых графическим методом. Больше задач — в видеокурсе «Графический метод решения задач с параметрами» (бесплатно).
1. При каких значениях параметра a уравнение имеет ровно 2 различных решения?
Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю.
В первом уравнении выделим полный квадрат:
Это уравнение окружности с центром в точке и радиусом равным 2. Обратите внимание — графики будем строить в координатах х; а.
Уравнение задает прямую, проходящую через начало координат. Нам нужны ординаты точек, лежащих на окружности и не лежащих на этой прямой.
Для того чтобы точка лежала на окружности, ее ордината а должна быть не меньше 0 и не больше 4.
Точка С также не подходит нам, поскольку при мы получим единственную точку, лежащую на окружности, и единственное решение уравнения.
2. Найдите все значения a, при которых уравнение имеет единственное решение.
Уравнение равносильно системе:
Мы возвели обе части уравнения в квадрат при условии, что (смотри тему «Иррациональные уравнения»).
Раскроем скобки в правой части уравнения, применяя формулу квадрата трехчлена. Получаем систему.
Приводим подобные слагаемые в уравнении.
Заметим, что при прибавлении к правой и левой части числа 49 можно выделить полные квадраты:
Решим систему графически:
Исходное уравнение имеет единственное решение, если окружность имеет единственную общую точку с полуплоскостью. Другими словами, окружность касается прямой, заданной уравнением
Пусть С — точка касания.
Рассмотрим треугольник ABP. Он прямоугольный, и радиус окружности PC является медианой этого треугольника. Значит по свойству медианы прямоугольного треугольника, проведенной к гипотенузе.
Из треугольника ABP найдем длину гипотенузы AB по теореме Пифагора.
Решая это уравнение, получаем, что
3. Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение.
Второе уравнение при задает окружность с центром в точке и радиусом a.
Вот такая картинка, похожая на злую птицу. Или на хрюшку. Кому что нравится.
, (как гипотенуза прямоугольного треугольника МNР с катетами 3 и 4),
В — точка касания окружности и окружности
длину MQ найдем как гипотенузу прямоугольного треугольника KMQ с катетами 7 и 4; Тогда для точки В получим:
Есть еще точки С и D, в которых окружность касается окружности или окружности соответственно. Однако эти точки нам не подходят. В самом деле, для точки С:
, но и это значит, что окружность с центром в точке М, проходящая через точку С, будет пересекать левую окружность и система будет иметь не одно, а три решения.
Аналогично, для точки D:
и значит, окружность с центром М, проходящая через точку D, будет пересекать правую окружность и система будет иметь три решения.
4. При каких значениях a система уравнений имеет 4 решения?
И в первом, и во втором уравнении системы уже можно разглядеть известные «базовые элементы» (ссылка) — в первом ромбик, во втором окружность. Видите их? Как, еще нет? — Сейчас увидите!
Просто выделили полный квадрат во втором уравнении.
Сделаем замену Система примет вид:
Вот теперь все видно! Рисовать будем в координатах
Графиком первого уравнения является ромб, проходящий через точки с координатами и
Графиком второго уравнения является окружность с радиусом и центром в начале координат.
Когда же система имеет ровно 4 решения?
1) В случае, когда окружность вписана в ромб, то есть касается всех сторон ромба.
Запишем площадь ромба двумя способами — как произведение диагоналей пополам и как произведение стороны на высоту, проведенную к этой стороне.
Диагонали нашего ромба равны 8 и 6. Значит,
Сторону ромба найдем по теореме Пифагора. Видите на рисунке прямоугольный треугольник со катетами 3 и 4? Да, это египетский треугольник, и его гипотенуза, то есть сторона ромба, равна 5. Если h — высота ромба, то

2) Есть второй случай, и мы его найдем.
Пусть радиус окружности равен 3. Тогда система имеет 6 решений.
Значит, Объединим случаи и запишем ответ:
Больше задач и методов решения — на онлайн-курсе Анны Малковой. И на интенсивах ЕГЭ-Студии в Москве.
Виды геометрических моделей
Геометрическое моделирование
Пример.
Изменение масштаба.
Поворот осей;
Перенос в начало координат;
Пусть на плоскости задан отрезок прямой АВ: А(3,2) и В(-1,-1). Что произойдет с отрезком при полной смене координат наблюдателя, если: 1) начало координат переносится в точку (1,0);
2) произойдет поворот осей на угол
3) изменение масштаба по оси Х вдвое.
2) при повороте осей в новой с.к:
3) изменение масштаба, Sx=2
При решении большинства задач в области автоматизированного конструирования и технологии промышленного производства необходимо учитывать форму проектируемого объекта, поэтому в их основе лежит геометрическое моделирование.
Под геометрическими моделями понимают модели, содержащие информацию о геометрии изделия, технологическую, функциональную и вспомогательную информации.
Под геометрическим моделированием понимают весь процесс обработки от вербального (словесного на некотором языке) описания объекта в соответствии с поставленной задачей до получения внутримашинного представления.
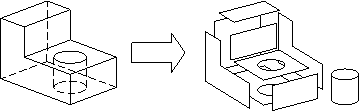
В геометрическом моделировании объект можно представить в виде:
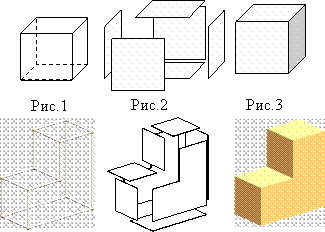
Ø Каркасная (проволочная) модель (рис. 1)
Ø Поверхностная (полигональная или фасетная) модель (рис. 2)
Ø Твердотельная (объемная) модель (рис. 3)
I) Каркасная: конструктивными элементами являются ребра и точки. Эта модель проста, но с ее помощью можно представить в пространстве только ограниченный класс деталей. Каркасные модели удобны для представления двумерных геометрических объектов на плоскости, на основе каркасной модели можно получать их проекции. Но в ряде случаев они дают неоднозначное представление и имеют ряд недостатков:
§ Неоднозначность, нельзя отличить видимые линии от невидимых, можно по-разному интерпретировать изображение;
§ Невозможность распознавания криволинейных граней, и, в следствии этого сложности тонирования;
§ Сложность обнаружения взаимного влияния компонентов.
Каркасные модели не используются для анимации. Возникают трудности при вычислении физических характеристик: объем, масса, и т.д. Используются такие модели преимущественно для самых общих построений.
II) Поверхностные модели: при построении такой модели предполагается, что технологические объекты ограничены плоскостями, которые ограничивают их от окружающей среды. Конструктивными элементами являются точки, ребра и поверхности. Здесь используются также различные криволинейные поверхности, что позволяет задавать тоновые изображения.
Поверхность технологического объекта, как и в каркасном моделировании, получается ограниченной контурами, но в полигонном моделировании эти контуры являются результатом двух касающихся или пересекающихся поверхностей. Здесь часто используются аналитические кривые, т.е исходные кривые описываемые некоторой сложной математической зависимостью.
Поверхностные модели дают возможность удобства скульптурного изображения, т.е любую поверхность можно внести как элементарную и в дальнейшем использовать ее для формирования сложных изображений. Использование таких поверхностных моделей позволяет легко изобразить сопряжение поверхностей.
Недостатком полигонного моделирования является то, что чем больше задающих поверхностей необходимо для описания объекта, тем сильнее полученная модель будет отличаться от его реальной формы, и тем выше количество обрабатываемой информации, а значит и определенные сложности в воспроизведении первоначального объекта.
III) Твердотельные модели. Конструктивными элементами твердотельных моделей являются: точка, контурный элемент и поверхность.
Для объемных моделей объектов существенно разграничение точек на внутренние и внешние, по отношение к объектам. Для получения таких моделей сначала определяются поверхности, ограничивающие объект, и затем они собираются в объект.
Полное определение объемной формы, возможность автоматического построения разрезов, сборок, удобное определение физических характеристик: массы, объема, и т.д., удобная анимация. Это используется для моделирования, обработки различными инструментами любых поверхностей.
Разнообразная палитра цветов дает возможность получения фотоизображения.
В качестве базовых примитивов используются различного вида отдельные элементы: цилиндр, конус, параллелелепипед, усеченный конус.
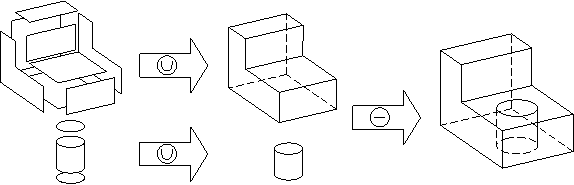
В основе построения сложных объемов из примитивов лежат булевы операции:
Их использование базируется на теоретико-множественном представлении об объекте как множестве точек принадлежащих тому или иному телу. Операция объединения предполагает объединение всех точек принадлежащих обоим телам (объединение нескольких тел в одно); пересечение – всех точек, лежащих на пересечении (результат- тело, которое содержит частично оба исходных тела); разность – вычитание одного тела из другого.
Все эти операции могут применяться последовательно над базовыми элементами и промежуточными результатами, получая нужный объект.
Таким образом строятся все детали в машиностроении: добавляются бобышки, вырезаются отверстия, пазы, проточки, и т.д.
Обособленным случаем объемной модели являются конструктивные модели, в которых геометрические объекты представляются в виде структур. Известны следующие способы построения таких структур:
1. Объем определяется как совокупность ограничивающих его поверхностей.
2. Объем определяется комбинацией элементарных объемов, каждый из которых обращается в соответствии с пунктом 1.
3D Моделирование позволяет самое удобное получение физических характеристик, удобно для выполнения имитации механической обработки.
В настоящее время существует большое число пакетов 3D моделирования. Остановимся на UNIGRAPHICS. (HP)
9.2. Система UNIGRAPHICS. (CAD/CAM – система).
Система Unigraphics имеет модульную структуру. Каждый модуль выполняет определенные функции. Все функциональные модули Unigraphics вызываются из управляющего модуля, который называется Unigraphics Gateway («ворота»). Это базовый модуль, который «встречает» пользователя при запуске Unigraphics, когда ни один прикладной модуль еще не запущен. Как бы олицетворяет собой фойе (Geteway) в здании Unigraphics.
После завершения проектирования имеется возможность разработки технологического процесса для изготовления детали.
Система Unigraphics имеет более 20 модулей.
1.Создание 3-х мерной модели в модуле Modeling/Моделирование.
Рассмотрены возможности создания моделей по эскизам, описан процесс образования тела, рассмотрено построение тела при помощи листовых поверхностей. Рассмотрено создание собственного типового элемента.
2.Разработка сборочной единицы с применением модуля Assemblies/Сборки.
Данный модуль позволяет скомпоновать сборочную единицу. Несколько моделей могут быть собраны по условиям сопряжения поверхностей, либо растиражированы в единый сборочный узел.
3.Испытания детали с применением модуля Analyze/Структурный анализ.
При проектировании часто возникает необходимость испытания детали. Это необходимо для того, чтобы еще на ранних этапах проектирования выявить недостатки конструкции и найти так называемые «слабые места». Для испытания детали в UG существует модуль Структурный Анализ.
4.Создание конструкторской документации с помощью модуля Drafting/Черчение.
В этом модуле рассмотрены общие принципы создания конструкторской документации в CAD/CAM/CAE системе Unigraphics. Приведены особенности настроек различных параметров, методы установки размеров, работа со слоями, шаблонами и таблицами, а также параметры вывода документов на печать.
5.Разработка технологического процесса для изготовления детали с применением модуля Manufacturing/Обработка.
Модуль обработки позволяет в интерактивном режиме программировать и обрабатывать постпроцессором траектории инструмента для операций фрезерования, сверления, токарной и электроэрозионной обработки.
1.Один из главных модулей пакета является Modelingс помощью которого выполняется построение твердотельной геометрической модели. Моделирование ведется на основе типовых элементов и операций. При необходимости пользователь может использовать любое созданное тело как базовое.
Эскиз – набор функций который позволяет задать плоский контур кривых, управляемых размерами.
Используется своя терминология:
Feature – типовой элемент формы.
Body – тело, класс объектов, которое состоит из двух видов: объемное тело, либо листовое тело.
Sheet body – тело, состоящее из граней и ребер, которые не замыкают объем – листовое тело.
Face – часть внешней поверхности тела, которая имеет одно уравнение для своего описания.
Edge – кривые, которые ограничивают грань.
Part – часть проекта.
Язык выражений.
Используется язык выражений, синтаксис которого напоминает язык С. Можно задать переменные, набор операций, можно определить выражение, которое описывает некоторую часть, и, импортировать в другие части. Используя механизм передачи выражений между частями можно моделировать зависимость между компонентами сборки. Например, некоторая заклепка может зависеть от диаметра отверстия. При изменении диаметра отверстия автоматически изменится и диаметр этой заклепки, если они связаны.
Типовые элементы формы.
Ø Заметаемые тела – на основе эскиза перемещением в прямом направлении.
Ø Тела вращения – получается от эскиза или плоского тела вращением вокруг оси (параллелепипед, цилиндр, конус, сфера, труба, бобышка)
Булевы операции.
9.2.1.Модуль Modeling/Моделирование.
Одним из главных модулей UG является Modeling,с помощью которого выполняется построение твердотельной геометрической модели. Моделирование ведется на основе типовых элементов и операций. При необходимости можно использовать любое созданное тело как базовое.
Преимущества твердотельного моделирования:
ü Богатый набор типовых методов построения твердого тела;
ü Возможность управления моделью с помощью изменения параметров;
ü Легкость редактирования;
ü Высокая производительность;
ü Возможность концептуального проектирования;
ü Лучшая визуализация модели,
ü Модель создается за меньшее количество шагов;
ü Возможность создания “мастер-модели”, способной поставлять информацию в такие приложения как черчение и программирование для станков с ЧПУ;
ü Автоматическое обновление чертежа, программы для станка и т.д. при изменении геометрической модели;
ü Простой, но точный способ оценки массово-инерционных характеристик модели.
Среди методов твердотельного моделирования UNIGRAPHICS предлагает:
Эскиз – набор функций, который позволяет задать плоский контур кривых, управляемых размерами.
Можно использовать эскиз для быстрого задания и определения размеров для любой плоской геометрии. Эскиз может быть вытянут, повернут либо протащен вдоль произвольной заданной направляющей. Все эти операции приводят к построению твердого тела. В дальнейшем можно изменить размеры эскиза, поменять на нем размерные цепочки, изменить наложенные на него геометрические ограничения. Все эти изменения приведут к модификации как самого эскиза, так и твердотельного тела, которое на нем построено.
Моделирование на базе типовых элементов и операций
Используя метод типовых элементов и операций, можно легко создать сложное твердое тело, имеющее отверстия, карманы, пазы и другие типовые элементы. После создания геометрии есть возможность прямого редактирования любого из использованных элементов. Например, изменить диаметр и глубину ранее заданного отверстия.
Собственные типовые элементы
Если не достаточен стандартный набор типовых элементов, то можно легко его расширить, объявив любое созданное тело как типовое и, задав параметры, которые должны вводиться пользователем при его использовании.
Ассоциативность – взаимосвязь элементов геометрической модели. Эти зависимости устанавливаются автоматически, по мере создания геометрической модели. Например, сквозное отверстие автоматически ассоциируется с двумя гранями твердого тела. После этого любые изменения этих граней автоматически вызовут изменение отверстия, так что его свойство `протыкать` модель насквозь сохранится.
Позиционирование типовых элементов
Возможно использование функции размерного позиционирования элементов для того, чтобы правильно определить их положение на твердом теле. Позиционные размеры так же обладают свойством ассоциативности и помогут сохранить целостность описания модели при ее дальнейшем редактировании. Кроме того, можно изменять положение элементов простым редактированием размеров.
Ссылочные типовые элементы
Создаются такие ссылочные элементы, как координатные оси и плоскости. Эти элементы удобно использовать для ориентации и позиционирования других типовых элементов. Координатные плоскости, например, удобно использовать для задания положения эскиза. Координатная ось может использоваться как ось вращения, либо как прямая до которой задается размер. Все ссылочные элементы сохраняют свойство ассоциативности.
Возможность добавления в модель необходимых соотношений, используя возможность задания параметров в виде математических формул любой сложности, содержащих даже условный оператор “если”.
При построении твердого тела система допускает логические операции объединения, вычитания и пересечения. Эти операции могут использоваться как для сплошного, так и листового твердого тела.
9.2.2. Модуль Assemblies/Сборки.
Этот модуль предназначен для конструирования сборочных единиц (узлов), моделирования отдельных деталей в контексте сборки.
Устанавливаются ассоциативные связи сборки с ее компонентами для упрощения процесса проведения изменений на различных уровнях описания изделия. Особенность использования сборки заключается в том, что конструкторские изменения одной детали отражаются на всех сборках, использующих эту деталь. В процессе построения сборки не нужно заботится о геометрии. Система создает ассоциативные связи сборки с ее компонентами, которые обеспечивают автоматическое отслеживание изменений геометрии. Существуют различные способы построения сборки, которые позволяют детали или подсборки друг с другом.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет