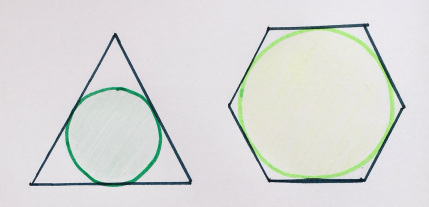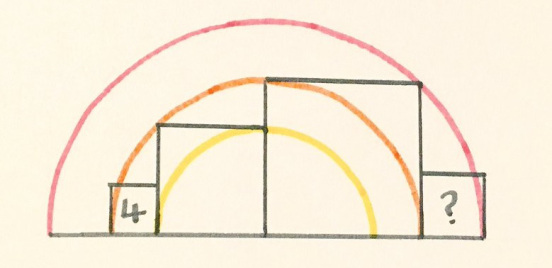Что такое геометрическая задача
Геометрические задачи и методы их решения с примерами
Содержание:
Логическое построение геометрии
Чтобы отличать геометрические фигуры друг от друга, их свойства описывают в виде утверждения, которое называют определением. Однако, определить вес геометрические фигуры невозможно. Некоторые из них, первоначальные, вынуждены принять без определения. Принимаем их за неопределяемые, начальные (основные) геометрические фигуры. Логическое построение геометрии осуществляют в следующем порядке: 1. Вначале принимают основные (начальные) геометрические фигуры без определения; 2. Принимают основные свойства этих фигур без доказательств;
3. Определяют другие геометрические фигуры через основные фигуры и их свойства, а затем доказывают свойства этих фигур и утверждений, истинность которых устанавливается путем доказательств, опираясь на известные.
Такое построение науки называют аксиоматическим построением. Свойства фигур, принятые без доказательства, называют аксиомами.
В планиметрии, которую мы изучали до сих пор основными геометрическими фигурами были точка и прямая. Их приняли без определения. Но определили отрезок, луч, треугольник и другие геометрические фигуры. Точно так же следующие свойства (утверждения) мы принимаем без доказательств в качестве аксиом:
I. Аксиомы принадлежности
1.1. Какова бы ни была прямая на плоскости, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
1.2. Через любые две точки можно провести прямую, и притом только одну.
II. Аксиомы расположения
2.1. Из трех точек, лежащих на прямой, одна и только одна лежит между двумя другими.
2.2. Любая прямая делит плоскость на две части: на две полуплоскости.
III. Аксиомы измерения
3.1. Любой отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
3.2. Любой угол имеет определенную градусную меру, большую нуля. Градусная мера развернутого угла равна 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
IV. Аксиомы откладывания
4.1. На любом луче от его начальной точки можно отложить единственный отрезок, равный данному.
4.2. От любого луча в определенную полуплоскость можно отложить единственный угол, равный данному, не развернутому углу.
4.3. Для любого треугольника существует единственный равный ему треугольник в заданном расположении относительно данного луча.
V. Аксиома параллельности
5.1. На плоскости через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
Древнегреческий ученый Платон отмстил удивительную закономерность в геометрии: из свойств, изученных и доказанных ранее, логически размышляя и обдумывая, можно получить новые свойства. Следовательно, используя эти удивительные возможности, можно формулировать остальные свойства в виде теорем, которые доказывают с помощью логических размышлений, аксиом, а также свойств, доказанных до этого.
В процессе размышления запрещается использование недоказанных свойств, даже если их правильность очевидна.
В формировании геометрии в качестве самостоятельной науки большой вклад внесли древнегреческие ученые. Например, Гиппократ Хиосский дал разъяснения о первых геометрических понятиях. Наибольший вклад в этой области принадлежит великому древнегречеcкому ученому Евклиду (356-300 годы до нашей эры). Его основной труд «Начала» содержит планиметрию, стереометрию и некоторые вопросы теории вероятностей, кроме того, алгебру, основы теории отношений, способы вычисления площадей и объемов и также элементы теории пределов. Евклид в «Началах» собрал все достижения древнегреческих математиков того времени и создал основу для дальнейшего развития математики.
I. Через любые две точки можно провести только одну прямую.
II. Отрезок прямой можно бесконечно продолжить.
III. Из любой точки можно построить окружность произвольныго радиуса.
IV. Все прямые углы равны между собой.
V. Если две прямые, лежащие в одной плоскости, пересеченные третьей, образуют внутренние углы, сумма которых меньше двух прямых углов, то при продолжении вышеупомянутых прямых они пересекутся с той стороны, где сумма углов меньше двух прямых углов.
Упомянутый труд получил огромную славу и признание. Особенно V постулат стал причиной большой научной дискуссии. Если обозначить внутренние углы в V постулате а и (3 (рис. 1), а прямые а и b, то по смыслу этого постулата а+(3
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Двадцать задачек (по безумной, восхитительной геометрии)
Предупреждение врача. Остерегайтесь этих головоломок. Побочные эффекты могут включать потерянное послеобеденное время, скомканные волосы и восклицания «А-а-а-х, вот как это делается» настолько громкие, что могут треснуть оконные стёкла.
Несколько месяцев назад я наткнулся в твиттере на математические головоломки Катрионы Ширер. Они сразу меня увлекли: каждая головоломка такая осязаемая, ручной работы, словно просит её решить. И на каждую вы можете легко потратить час времени, а то и больше.
Катриона разрешила мне подвесить вас на эти задачки — и поделилась 20 своими любимыми головоломками. Она даже удовлетворила моё любопытство и восхищение, дав интервью (см. в конце статьи).
Наслаждайтесь. И не говорите, что врач не предупреждал.
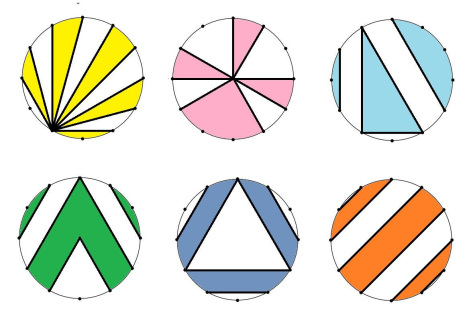
1. Сад часов
Какая часть каждого круга закрашена? (12 точек на равном расстоянии; единственная точка внутри круга — его центр)
«К сожалению, из эти шести моя любимая — единственная, которую я не придумала сама, — говорит Катриона, — это тёмно-синяя».
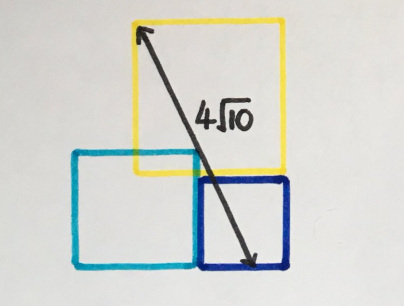
2. Опрокинутый квадрат
(Как по мне, это классика).
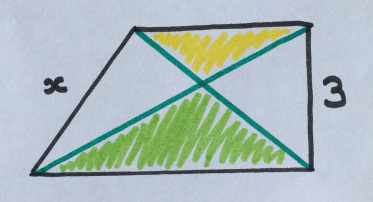
3. Это ловушка
В прямоугольной трапеции зелёная область на 6 больше, чем жёлтая. Чему равен x?
«Это „вторая версия” данной головоломки: она лучше, чем первая, которую я придумала».
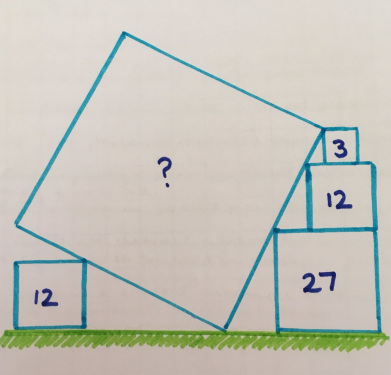
4. Три квадратных тарелки
Длины сторон трёх квадратов — последовательные целые числа. Какова общая площадь?
«Эта мне очень нравится: на её основе я нарисовала много красивых узоров».
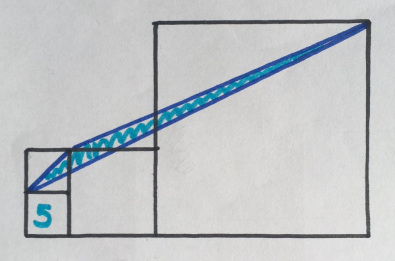
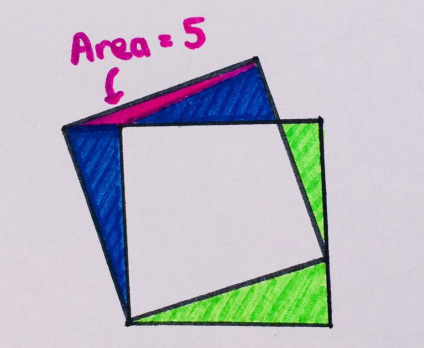
5. Красивая стрижка
Площадь левого нижнего квадрата 5. Какова площадь синего треугольника?
«Наверное, моя любимая за всё время. Выглядит просто невозможным! Здесь метод решения называется «стрижка», shearing (к сожалению, не в мою честь)».
6. Все люди рождены равными
«Ещё одна переделка, которую я предпочитаю оригиналу».
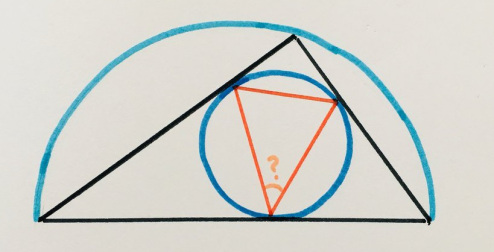
7. Полукруг турдакен
«Головоломки с углами гораздо труднее составлять. Ученики сказали, что это довольно простая задачка, но мои родители испытали большие трудности. Кажется, эта головоломка требует больше „знаний”, но сам процесс решения проще».
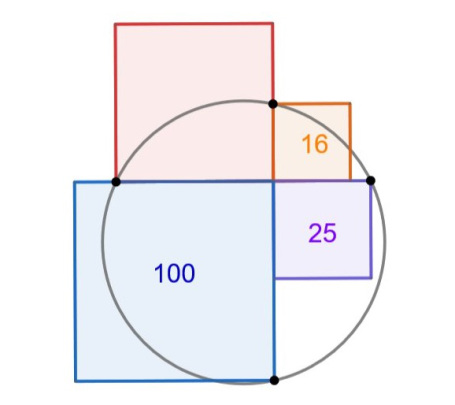
8. Степенные хорды
Какова площадь круга?
«В школе я не изучала теорему о пересекающихся хордах, поэтому люблю везде её использовать!»
9. Сказка о двух кругах
У этих правильных многоугольников одинаковый периметр. Найдите отношение площадей вписанных окружностей.
«Это следствие другой головоломки, но она мне нравится больше, чем оригинал!»
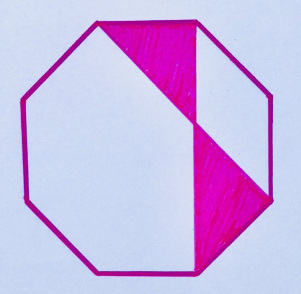
10. Doc Oct
У закрашенной области такое же значение, как у периметра правильного восьмиугольника. Каково значение?
«Думаю, это довольно чистая задачка, хотя выглядит как массовое разграбление головоломок Эда Сауталла».
11. Всё в квадрате
«Мне нравится то, что хотя вы здесь можете найти все стороны оранжевого треугольника (и я это сделала, когда решала), но на самом деле это не нужно — достаточно площади и гипотенузы».
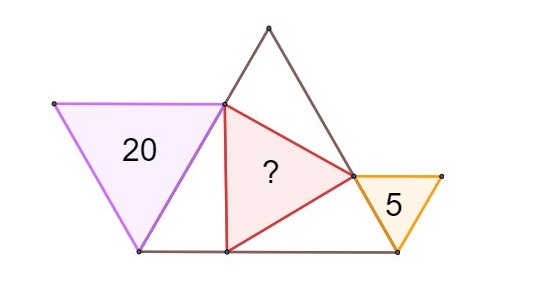
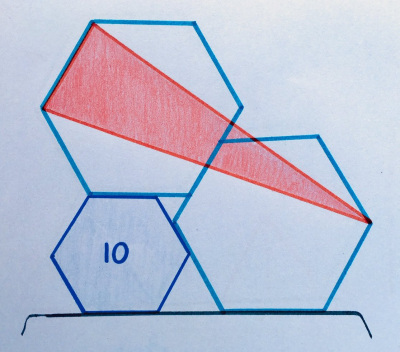
12. Шип в улье
Два из правильных шестиугольников идентичны; у третьего площадь 10. Какова площадь красного треугольника?
«Довольно неплохо: мне нравится, что не нужно иметь дело с любой длиной стороны, которые почти наверняка ужасны».
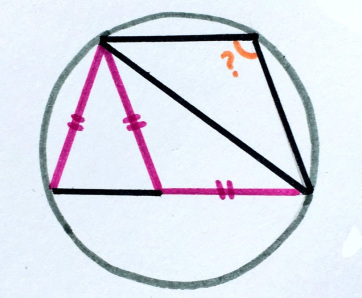
13. Я видел равнобедренных
Все четыре треугольника равнобедренные. Найдите угол.
«Думаю, что формулировка этой задачки идеальна. Многие пропускают важную информацию и приходят к выводу, что есть бесконечное число решений!»
14. Зеленый против синего
На картинке больше зелёного цвета или синего (и на сколько)?
«Ещё одна из моих любимых».
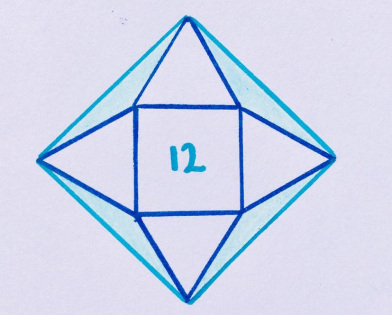
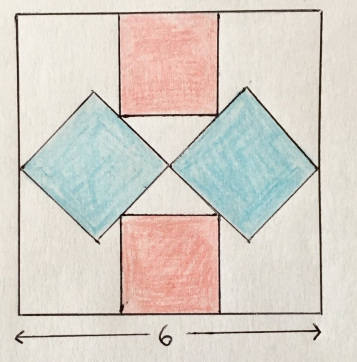
15. Резцы по камню
Четыре равносторонних треугольника расположены вокруг квадрата с площадью 12. Какова закрашенная площадь?
«Тут самое лучшее — действительно хорошие решения по рассечению площади».
16. Едем, едем, уехалиугольник
Шесть одинаковых квадратов и меньший прямоугольник вписаны в этот правильный шестиугольник. Какую часть шестиугольника они занимают?
«Здесь ответ не такой красивый, но очень удивил меня. Думаю, из-за своей сложности эта задачка не получила такого распространения в твиттере, как другие!»
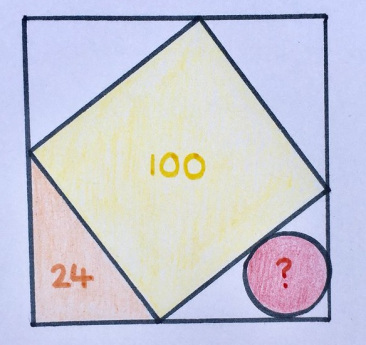
17. Только один факт
Какова площадь этого квадрата?
«Это одна из моих любимых, потому что сначала кажется, что информации недостаточно».
18. Стиральная машина
Какая часть большого квадрата закрашена?
«Здесь мне нравится сумбур квадратов, как они грохочут вокруг словно в стиралке. И ответ тоже удивительно красивый».
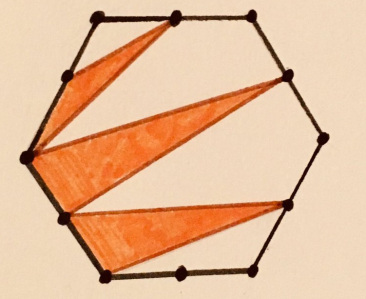
19. Летающие флаги
У квадратов одного цвета одинаковый размер. Какова площадь всех закрашенных областей?
«Это довольно просто, как только вы поймёте — но я поняла не сразу, поэтому простота ответа меня удивила».
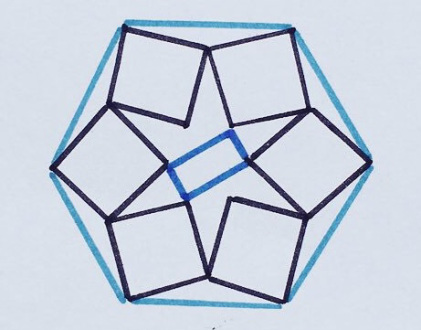
20. Тигрогон
Какая часть фигуры закрашена? Шестиугольник правильный, с равномерно расположенными точками по периметру.
«Эту я редко публиковала. Но картинка напоминает мне Тигра Тони [с пачек быстрого завтрака Kellogg — прим. пер.]».
БОНУС:
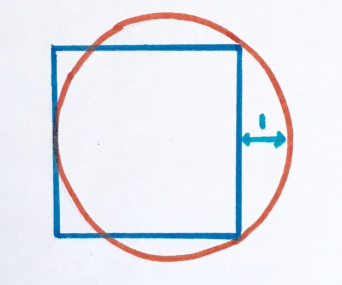
Закат над Квадратным городом
У левого квадрата площадь 4. Какова площадь правого квадрата?
«Мне нравится эта задачка, она напоминает закат над городом скверов.”
Если вы дочитали до этого места — возможно, через 6 месяцев после начала чтения — и ваш стол окружен скомканными бумагами и пустыми китайскими контейнерами для продуктов питания, то вам будет приятно почитать небольшое интервью с Катрионой.
Как вы пришли к разработке своих головоломок?
Я поехала в отпуск в Шотландское высокогорье, но забыла взять пальто, поэтому пришлось сидеть в домике в одиночестве, пока друзья гуляли на природе! Ничего не оставалось, кроме как машинально чертить линии на бумажке.
Не ожидала, что это превратится в хобби, но это немного затягивает, особенно когда люди присылают в ответ свои решения, которые мне нравятся. Почти всегда можно красиво сократить головоломку, что я пропустила.
Как проходит творческий процесс?
Всё начинается с рисования бессмысленных фигурок. В итоге получается целая страница перекрывающихся квадратов под разными углами или правильных (типа) пятиугольников с разными закрашенными частями, а потом я смотрю, есть ли там какая- то хорошая математика — отношения между длинами или площадями или углами.
Многие из ваших задачек нарисованы маркером на бумаге. Почему такой лоутек?
Я пробовала использовать Desmos и Geogebra, но не очень понравилось. По-моему, быстрее нарисовать вписанный круг вручную, после небольшого количества проб и ошибок, чем красиво строить его в геометрии программного обеспечения.
Кроме того, при использовании фломастера вы можете выдумывать вещи, потому что линии настолько толстые. Это хороший компромисс между тем, чтобы выглядеть «правильно», но также знать, что вы не можете просто вытащить линейку и измерить фигуру.
Одна из приятных вещей в геометрии — что она многое прощает. Я могу показать вам безнадёжный квадрат или круг, но этого достаточно, чтобы передать концепцию, потому что они так хорошо определены.
Некоторые из ваших головоломок дают самый минимум информации. Как вы находите эту границу, где диаграмма как раз определена?
Иногда этот минимум на самом деле подсказка, потому что он отправляет вас по одной дороге. Я предпочитаю давать чуть больше необходимого, поэтому есть несколько обманных маршрутов. Это также даёт большее разнообразие решений!
Было дело, я опубликовала пару невозможных головоломок: к счастью, кто-нибудь обычно указывает на это довольно быстро!
Я также публиковала задачки с массивным количеством излишней информации, потому что не видела хорошего решения, чтобы использовать только половину информации.
Советы для потенциальных создателей головоломок?
Отлично, тут мой синдром самозванца полностью проявится. Я определённо ещё новичок — я занимаюсь этим только с августа [статья опубликована в октябре 2018 года — прим. пер.]! С другой стороны, мне нравится создавать головоломки и читать решения даже больше, чем решать их самой.
Основной целью головоломки должно быть развлечение — вот что отличает её от стандартной математической задачи. Таким образом, вам нужно по крайней мере два из трёх:
Как решать задачи по геометрии. Часть 1
Геометрическая логика при решении задач
Геометрия… Страшное слово для бесчисленного множества учеников. Они знают свойства фигур и выучили определения и теоремы, но задачи по геометрии все равно остаются какой-то китайской грамотой.
Это про тебя? Тогда ты попал туда, куда нужно!
Проблема подавляющего большинства учеников в том, что они не умеют обдумывать задачу по геометрии. Их этому не научили (ну, или они не захотели научиться, когда была возможность). Именно в этой статье, я объясню саму технологию обдумывания и, в конечном счете, нахождения решения ПРАКТИЧЕСКИ ЛЮБОЙ задачи по геометрии.
Ты играл когда-нибудь в квесты? Неважно в реальной жизни или в компьютере. Во всех квестах принцип один – у тебя есть что-то (вещи, знания, навыки) и есть цель (раскрыть какую-нибудь тайну, найти некий предмет, «спасти принцессу» и т.д.). При этом путь к цели – неизвестен. И зачем нужны эти самые имеющиеся у тебя «вещи, знания, навыки» – тоже непонятно. Что делать? Как достичь цели?
Известно как: использовать то, что есть, и искать, куда это применить, чтоб продвинуться к цели. То есть, делать шаги от своего текущего местонахождения – к цели. При этом понятно, что некоторые шаги будут вести нас не туда, куда надо, а совсем даже в тупик. А иногда мы будем находить вещи или информацию, вроде бы напрямую к цели не ведущие, но как выяснится в дальнейшем – необходимую.
Более того, порой можно логически двигаться и наоборот – от цели к твоей текущей позиции. Например, если нужно «спасти принцессу из замка», то понятно, что, скорее всего, надо будет как-то попасть в замок. А для этого надо оказаться на острове, где этот замок стоит. Как попасть? Может быть на лодке. Или найти телепорт. Или использовать магию. Но на остров – надо. Начинаем искать пути на остров. Это уже логические шаги от цели к текущей позиции.
Ладно, давай уже конкретный пример разберем.
Задача. В треугольнике \(ABC\) из точки \(B\) проведена высота \(BH\). Найти длину отрезка \(AH\), если известно, что сторона \(AC\; =\; 14\) см и угол \(A\) равен углу \(C\).
Так. С чего начинается решение геометрической задачи? Ну, а с чего начинается решение квеста? Правильно, осматриваемся по сторонам, изучаем, что у нас есть и куда нас жизнь закинула.
В геометрии это означает:
Хорошо. Значит, текущая ситуация у нас такова:
Давайте потихоньку развеивать туман. Нам известно, что углы \(А\) и \(С\) равны, а это значит, что треугольник \(АВС\) – равнобедренный с основанием АС (теория – «признак равнобедренного треугольника: равенство углов при одной из сторон. Она и является основанием»). Это новая информация, новые данные, изначально неизвестные. Делаем шаг.
Отлично. Теперь смотрим, что у нас есть еще? Еще у нас есть информация, что \(BH\) – высота. А раз треугольник \(ABC\) – равнобедренный, то значит \(BH\) еще и медиана (теорема о высоте в равнобедренном треугольнике: высота, проведенная к основанию равнобедренного треугольника является медианой и биссектрисой). То есть, мы, используя новые, полученные на предыдущем шаге данные, а также исходные данные и знание теории, делаем еще один шаг и опять получаем новую информацию.
А что мы знаем про медиану? Она делит противоположную сторону на две равные части (определение медианы: отрезок, соединяющий вершину треугольника с серединой противоположной стороны). Но тогда получается, что точка \(H\) делит сторону \(AC\) пополам. То есть \(AH = HC\).
Стоп. Так у нас же есть длина стороны \(AC\)! И если мы знаем, что точка \(H\) делит сторону \(AC\) пополам, значит, \(AH\) равен половине \(AC\)! Таким образом, получаем, что \(AH = AC/2 = 14/2=7\) см.
Готово. Ответ получен.
Естественно, такие конструкции с «пятном тумана» рисовать каждый раз не нужно, эта схема показывает логическую цепочку решения у нас в голове. А записывается примерно так:
Структура и виды геометрических задач (обобщение опыта)
В статье «Структура и виды геометрических задач» геометрическая задача разбита на её составляющие части, которым дана подробная характеристика. Разобраны все основные виды геометрических задач с приведением примеров текста и решения. Работа будет полезна начинающим учителям математики и студентам педагогических ВУЗов.
Просмотр содержимого документа
«Структура и виды геометрических задач (обобщение опыта) »
МБОУ «Большеусинская средняя общеобразовательная школа»
Чепкасова Ольга Васильевна,
Обучение решению геометрических задач
Решение задач занимает в математическом образовании огромное место. Психологические исследования проблемы обучения решению задач показывают, что основные причины несформированности у учащихся общих умений и способностей в решении геометрических задач состоят в том, что школьникам не даются знания о сущности задач и их решений, а поэтому они решают задачи, не осознавая свою собственную деятельность. У учащихся не вырабатываются отдельно умения и навыки в действиях, входящих в деятельность по решению задач, и поэтому им приходится осваивать эти действия в самом процессе решения задач, что многим школьникам не под силу. Не стимулируется постоянный анализ учащимися своей деятельности по решению задач и выделению в них общих подходов и методов, их теоретического обоснования и осмысления.
В первой главе показаны составные части задачи, их взаимосвязь, приведены примеры схематических записей, обоснована необходимость вычленения частей задачи
I. Составные части задачи
Решение задачи – это работа несколько необычная, а именно умственная работа. А чтобы научиться какой-либо работе, нужно предварительно хорошо изучить тот материал, над которым придётся работать.
Значит, для того чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких составных частей они состоят, каковы инструменты, с помощью которых производится решение задач.
Если приглядеться к любой задаче, то увидим, что она представляет собой требование или вопрос, на который надо найти ответ, опираясь и учитывая те условия, которые указаны в задаче. Поэтому, приступая к решению какой-либо задаче, надо её внимательно изучить, установить, в чём состоят её требования (вопросы), каковы условия, исходя из которых, надо решать задачу. Всё это называется анализом задачи.
I. 1.Условия и требования задачи
Естественно перед решением задачи её нужно внимательно прочитать. Первое, что мы замечаем при чтении задачи, состоит в следующем: в ней имеются определённые требования и утверждения. Часто требование в задаче формулируется в виде вопроса, но всякий вопрос предполагает требование найти на него ответ, а поэтому всякий вопрос можно заменить требованием. Формулировка любой задачи состоит из нескольких утверждений и требований. Утверждения задачи называются условиями задачи (иногда условием задачи называют всю формулировку задачи, т.е. условие и требования вместе).
1. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной 5см и 12см. Найти катеты треугольника.
В этой задаче утверждается, что «в прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной 5 см и 12 см». Требование задачи состоит в том, что нужно «найти катеты треугольника».
Далее можно вычленить такие элементарные условия:
в него вписана окружность;
точка касания делит гипотенузу на два отрезка;
длина одного отрезка 5 см;
длина другого 12см.
Требование этой задачи можно расчленить на два элементарных требования:
найти длину одного катета треугольника;
найти длину другого катета треугольника.
2. Из всех цилиндров заданного объёма наитии цилиндр с наименьшей полной поверхностью.
Условие этой задачи («из всех цилиндров заданного объёма») можно понимать так, что рассматривается множество цилиндров, объём которых равен некоторому числу V (здесь V является параметром). Требование задачи состоит в том, чтобы из заданного множества цилиндров найти такой, полная поверхность которого наименьшая. Соотнесём это требование с указанным условием. Ясно, что полная поверхность рассматриваемых цилиндров выступает в качестве переменной величины. Надо найти минимум этой переменной. Для этого, эту переменную следует представить как функцию от другой переменной. В качестве последней можно взять радиус основания цилиндра. Итак, условия задачи таковы:
1) рассматривается множество цилиндров, объём которых равен V (V – параметр);
2) радиус основания этих цилиндров есть переменная r;
3) полная поверхность S этих цилиндров есть некоторая функция S(r).
найти такое значение r, при котором S(r) принимает наименьшее значение.
Направленность анализа задачи на её требования состоит ещё и в том, что особое внимание необходимо уделить выяснению сущности требования задачи, четкому определению того, что нужно найти, сделать в задаче.
Для некоторых более сложных задач рассмотренный выше анализ (расчленение задачи на отдельные условия и требования) целесообразно продолжить. А именно установить, как устроены вычлененные условия. Анализируя эти условия, можно заметить, что каждое из них состоит из одного или нескольких объектов и некоторой их характеристики.
Рассмотрим пример: К двум окружностям, радиусы которых 4см и 6см, проведены внутренние общие касательные, оказавшиеся взаимно перпендикулярными. Вычислить расстояние между центрами окружностей.
Эта задача содержит такие условия:
дана окружность центра О1, радиус которой 4 см;
из некоторого другого центра О2 проведена окружность радиуса 6см;
эти две окружности построены так, что к ним можно провести общие внутренние касательные;
общие внутренние касательные к этим двум окружностям взаимно перпендикулярны.
Так объектом первого условия является окружность, а её характеристикой: радиус этой окружности равен 4см. Во втором условии объект – окружность с характеристикой: её радиус 6см. В третьем условии два объекта: указанные выше окружности, а характеристикой является их взаимное расположение на плоскости: они расположены так, что к ним можно провести внутренние общие касательные. Наконец, четвёртое условие содержит два объекта: общие внутренние касательные к окружностям, в качестве характеристики указано их отношение: они взаимно перпендикулярны.
Итак, в каждом условии задачи имеется один или два (в некоторых случаях больше) объекта; если в условии один объект, то указывается его характеристика в виде некоторого свойства этого объекта; если же объектов два, то характеристикой служит некоторое отношение этих объектов.
Возникает вопрос: нужен ли такой анализ для решения задачи? Ведь обычно, решая задачи, мы не производим такого анализа. Но мы этого просто не замечаем, ибо обычно такой анализ производится устно по ходу решения.
I. 2. Схематическая запись задач
Результаты предварительного анализа задач надо как-то зафиксировать, записать. Та словесная, описательная форма записи, которая приведена выше, конечно мало удобна. Нужна более удобная, боле компактная и в то же время достаточно наглядная форма записи анализа задачи. Такой записью является схематическая запись задачи. Для схематической записи геометрической задачи полезно использовать чертёж той фигуры, которая рассматривается в задаче. При построении такого чертежа надо выполнять ряд требований. Укажем некоторые из них:
1. Чертёж должен представлять собой схематический рисунок основного объекта задачи (геометрической фигуры, или совокупности фигур, или какой-то части этих фигур) с обозначением с помощью букв и других знаков всех элементов фигуры и некоторых её характеристик. Если в тексте задачи указаны какие-либо обозначения фигуры или её элементов, то эти обозначения должны быть и на чертеже; если же в задаче никаких обозначений нет, то следует воспользоваться общепринятыми обозначениями или придумать наиболее удобные.
2. Этот чертёж должен соответствовать задаче. Это означает, что если в задаче в качестве основного объекта назван, например, треугольник и при этом не указан его вид (прямоугольный, равнобедренный и др.), то надо построить какой-либо разносторонний треугольник.
3. При построении чертежа нет необходимости выдерживать строго какой-либо определённый масштаб. Однако желательно соблюдать какие-то пропорции в построении отдельных элементов фигуры. Если по условию задачи сторона АВ треугольника АВС наибольшая, то это должно быть соблюдено на чертеже. Или если задана медиана треугольника, то соответствующий ей отрезок на чертеже должен проходить приблизительно через середину стороны треугольника и т.д.
4. При построении чертежей пространственных фигур необходимо соблюдать все правила черчения этих фигур. Там, где это можно и целесообразно, лучше строить какие-либо плоскостные сечения этих фигур.
Кроме чертежа, для схематической записи геометрических задач используется ещё краткая запись всех условий и требований задачи. В этой краткой записи, пользуясь принятыми на чертеже обозначениями, записываются все характеристики и отношения, указанные в условиях задачи. Название фигур или отдельных её частей желательно заменять записью их определений. Например, вместо того, чтобы писать: ABCD – трапеция, можно писать: AD || CD. В краткой записи можно использовать, там, где целесообразно, стандартные математические знаки (знак принадлежности, пересечения и т.д.)
Рассмотрим на примерах, как строятся схематические записи геометрических задач с помощью чертежей:
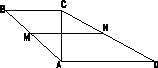
Диагональ трапеции перпендикулярна к её основаниям; тупой угол, прилежащий к большему основанию, равен 120 0 , а боковая сторона, прилежащая к нему, равна 7см; большее основание равно 12см. Найти среднюю линию трапеции.
Дано: 1) AB || CD; 2) AB

II. Сущность и структура решения геометрической задачи
Решение задачи не просто состоит в том, чтобы найти ответ. Если проанализировать решение какой-либо задачи, можно заметить что оно состоит из отдельных шагов, при этом каждый шаг решения есть применение какого-либо общего положения математики (правила, закона, теоремы, формулы) к отдельным условиям задачи или к полученным следствиям из этих условий.
II. 1. Что значит решить геометрическую задачу
Рассмотрим решение следующей задачи:
Длины оснований трапеции равны 4см и 10см. Найти длины отрезков, на которые делит среднюю линию этой трапеции одна из диагоналей.
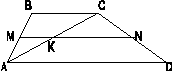
Сначала построим схематическую запись этой задачи (рис. 2):
Дано: AB||CD; AM = MD; BN = NC; AB = 10 см; CD = 4 см.
Решение: Средняя линия трапеции параллельна её основаниям. Значит, MN||AB и MN||CD. Диагональ АС делит трапецию на два треугольника. Рассмотрим каждый из них. В треугольнике АВС отрезок NK является средней линией, т.к. NK как часть отрезка MN параллельна АВ, и точка Nпо условию середина стороны BC. А средняя линия треугольника равна половине его основания. Значит, KN=0,5АВ, а т.к. АВ=10 см, то KN=5 см. Аналогично рассматривая треугольник АСD, получаем, что MK есть средняя линия треугольника и поэтому МК=0,5CD, но CD=4см, следовательно МК=2см.
Приведённое решение можно представить в виде такой схемы:
Общие положения математики
Условия задачи или их следствия
Средняя линия трапеции параллельна её основаниям
MN средняя линия трапеции ABCD
Диагональ делит трапецию на два треугольника
Отрезок, проходящий через середину стороны треугольника параллельно другой стороне, является средней линией треугольника
В треугольнике АВС точка N – середина стороны ВС и МК||АВ, в треуг. ACD точка М – середина AD и MK||CD
Средняя линия треугольника равна половине основания
NK – средняя линия треугольника АВС, АВ=10см;
KN=0,5АВ KN=5см МК=0,5CD, МК=2см.
Из приведённого примера можно сделать следующий вывод:
II. 2. Структура процесса решения задачи
В предыдущем разделе мы выписывали решения задач, но эти решения представляли лишь изложение самого решения. Но как эти решения были найдены, как убедились, что они правильные? Если под решение задачи понимать процесс, начинающийся с момента получения задачи до момента полного завершения её решения, то, очевидно, этот процесс состоит нетолько из изложения уже найденного решения, а из ряда этапов, одним из которых и является изложение решения.
Из каких же этапов состоит процесс решения задачи?
Тот анализ надо как-то оформить, записать. Для этого используются разного рода схематические записи, построение которых составляет второй этап процесса решения задачи.
Анализ задачи и построение её схематической записи необходимо главным образом для того, чтобы найти способ решения задачи. Этот поиск способа решения и составляет третий этап процесс решения задачи.
После того как решение осуществлено и изложено (письменно или устно), необходимо убедиться, что это решение правильное, что оно удовлетворяет всем требованиям задачи. Для этого производят проверку решения, что составляет пятый этап процесса решения задачи.
При решении многих задач, кроме проверки, необходимо ещё произвести исследование задачи, а именно установить, при каких условиях задача имеет решение и притом, сколько различных решений в каждом отдельном случае; при каких условиях задача вообще не имеет решения и т.д. Всё это составляет шестой этап процесса решения задачи.
Наконец, в учебных и познавательных целях можно произвести анализ выполненного решения, в частности установить, нет ли другого, более рационального решения, нельзя ли задачу обобщить, какие выводы можно сделать из этого решения ит.д. Всё это составляет последний, конечно необязательный, восьмой этап процесса решения задачи.
Структура процесса решения задачи зависит от характера задачи и, конечно, от того, какими знаниями и умениями обладает решающий задачу.
Приведённая выше схема процесса решения задачи является лишь примерной. При фактическом решении указанные этапы обычно не отделены друг от друга, а переплетаются между собой. Так, в процессе анализа задачи обычно производится и поиск пути решения. При этом план решения устанавливается не до осуществления решения, а в процессе. Тогда поиск решения ограничивается лишь нахождением идеи решения. Порядок этапов тоже может меняться.
Из указанных восьми этапов пять являются обязательными, и они имеются (в том или ином виде) в процессе решения любой задачи. Это этапы анализа задачи, поиска способа её решения, осуществления решения, проверка решения и формулирование ответа. Остальные три этапа (схематическая запись, исследование задачи и заключительный анализ решения) являются не обязательными.
II. 3.1. Стандартные и нестандартные задачи
Непосредственное решение задачи состоит из последовательных шагов (действий), каждый из которых есть применение некоторого общего положения математики к условиям задачи или к их следствиям. Поэтому отыскание этих шагов есть самое главное, что нужно сделать, чтобы решить задачу. Математика и занимается тем, что устанавливает для многих задач правила, пользуясь которыми можно установить последовательность шагов для решения любой задачи данного вида. Такие задачи называются стандартными. Для многих видов стандартных задач такие правила уже давно найдены. Эти правила в математике излагаются в различных формах.
1. Правило – определение: синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Отсюда ясна последовательность нахождения синуса (а следовательно и угла): найти противолежащий катет, найти гипотенузу, найти отношение.
2. Правило – теорема: средняя линия трапеции параллельна её основаниям и равна их полусумме. Программа решения проста: установить длину оснований, найти их полусумму. Это и будет длина средней линии трапеции.
Процесс решения стандартных задач имеет следующие особенности:
1)Анализ задачи сводится к установлению (распознаванию вида) вида задач, к которому принадлежит заданная.
2)Поиск решения состоит в составлении на основе общего правила или общего положения программы – последовательности шагов решения задач данного вида (если такая программа не рассматривается в курсе математики). Естественно, что нет надобности эту программу формулировать в письменном виде, достаточно её про себя наметить.
3)Само решение стандартной задачи состоит в применении общей программы к условиям данной задачи. Если же некоторые шаги программы решения требуют для своего выполнения также каких-то программ, то в отношении их производятся те же операции.
Отсюда следует, что, для того чтобы легко решать стандартные задачи (а они являются основными математическими задачами, а все остальные сводятся к ним):
— помнить (держать в памяти) все изученные в курсе математики общие правила (формулы, тождества) и общие положения (определения и теоремы).
— уметь развёртывать свёрнутые общие правила, тождества, формулы, определения и теоремы в программы – последовательности шагов решения задач соответствующих видов.
Нестандартные задачи – это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения. Рассмотрим пример с тем, чтобы выяснить особенности их решения.
Определить площадь равнобедренной трапеции, у которой основания равны 12см и 20см, а диагонали взаимно перпендикулярны.
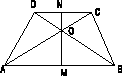
Решение: построим схематическую запись.
Дано: 1)АВ||CD, 2)AD=BC, 3)AC ┴ BD, 4)АВ=20 см, 5)CD=12 см.
Для вычисления площади трапеции имеется формула Sтр. = 0,5(a+b)h, где a и b – длины оснований трапеции, а h – длина её высоты.
Основания трапеции заданы; следовательно, задача сводится к нахождению высоты трапеции.
Проведём высоту трапеции (рис. 3). Это удобно сделать так: проводим через точку О (пересечение диагоналей) MN┴AB. Тогда MN и есть искомая высота h.
Рассматривая треугольники AOM и DON, получаем, что они прямоугольные и равнобедренные. Тогда ОМ = АМ = 10см, ON = DN = 6см. Следовательно, h = MN = MO + ON = 10 + 6 = 16 см.
Процесс решения этой задачи состоит из следующих этапов:
задачу вычисления площади трапеции свели к задаче нахождения высоты трапеции;
задачу нахождения высоты трапеции разбили на две подзадачи: а) нахождение отрезка OM высоты MN; б) нахождение длины отрезка ON той же высоты;
задачи 2 (а, б) свели к двум задачам: а) распознавание вида прямой MN по отношению к заданной трапеции; б) определение сторон OM и ON треугольников AOM и DON;
в результате решения задачи 3 (а) установили, что MN есть ось симметрии трапеции. Это даёт возможность найти AM и DN, а также углы AOM и DON;
Результаты решения задачи 4 и условие перпендикулярности диагоналей трапеции дают возможность установить, что треугольники AOM и DON прямоугольные и равнобедренные;
Следовательно, задача 3 (б) сводится к такой: найти катет прямоугольного равнобедренного треугольника, если известен другой катет.
Процесс решения любой нестандартной задачи состоит в последовательном применении двух основных операций:
1.Сведение (путём преобразования или переформулирования) нестандартной задачи к другой, ей эквивалентной, но уже стандартной задаче.
2.Разбиение нестандартной задачи на несколько стандартных задач.
В зависимости от характера нестандартной задачи используется либо одна из операций, либо обе. При решении более сложных задач эти операции применяются неоднократно.
II. 3.2.Распознавание вида задач.
1.Задачи на нахождение искомого. В задачах этого класса требование состоит в том, чтобы найти, распознать какое-то искомое. При этом искомым могут быть величина, отношение, какой-то объект, предмет, его положение, форма и т.д. Из геометрических задач сюда относятся вычислительные задачи, где нужно найти длину отрезка, величину угла, площадь фигуры, объём тела и т.п.
2.Задачи на доказательство или объяснение. В задачах этого класса требование состоит в том, чтобы убедиться в справедливости некоторого утверждения, или проверить верность или ложность этого утверждения, или объяснить, почему имеет место то или иное явление, тот или иной факт. Все задачи, требование которых начинается со слов «доказать», «проверить» или содержащие вопрос «Почему?», обычно относятся к этому классу задач.
3.Задачи на преобразование или построение. К этому классу из геометрических задач относятся те, в которых требуется преобразовать или построить какую-нибудь фигуру, удовлетворяющую заданным условиям. Характерной особенностью задач этого класса является то, что в каждой из них заданы какие-либо объекты, из которых требуется построить, сконструировать другой объект с заранее известными свойствами.
Установление вида задачи даёт возможность получить готовый план её решения: применить известный метод решения подобных задач. Конечно, встречаются задачи, определить вид которых не удаётся, тогда надо использовать другие приёмы (например, разбиение на подзадачи известного вида).
II.3.4. Поиск плана решения задачи путём сведения к ранее решённым задачам
Известный советский математик, профессор Московского университета С.Н. Янковская, выступая перед участниками олимпиад, на вопрос: «Что значит решить задачу?» дала простой, но неожиданный для слушателей ответ: «Решить задачу – значит свести её к уже решённым». Мы уже установили, что решение нестандартных задач состоит в сведении их путём преобразований или переформулирования к стандартным задачам, которые можно рассматривать как решённые ранее. Конечно, этот совет верен и простой, но практически им воспользоваться не так-то просто. Ведь нет определённых правил для сведения незнакомых задач к знакомым, уже решённым. Однако, если внимательно, вдумчиво анализировать задачу, решая задачи, фиксировать в памяти все приёмы, с помощью которых были найдены решения, то постепенно выработается умение в таком сведении.
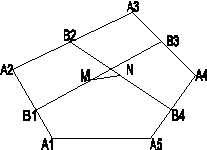
Рассмотрим пример: В произвольном выпуклом пятиугольнике вершины и стороны пронумерованы в порядке обхода по часовой стрелке. Середины первой и третьей сторон, а также второй и четвёртой соединены отрезками. Затем середины этих двух отрезков соединены также отрезком. Найдите длину последнего отрезка, если длина пятой стороны равна а.
Решение: Построим схематическую запись (рис.4).
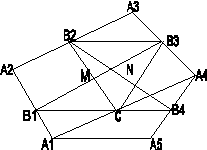
Видим, что задача явно незнакомого вида. К каким задачам её можно свести? Читая внимательно условие, обращаем внимание на то, что речь идёт о серединах сторон. Середины сторон встречаются в задачах на среднюю линию треугольника, среднюю линию трапеции. Известна также задача, где речь идёт о последовательном соединении середин сторон четырёхугольника. А нам дан пятиугольник. Естественно возникает идея отсечь от пятиугольника четырёхугольник. Только это надо удачно сделать. Удобно для этого соединить вершины А1 и А4. В полученном четырёхугольнике А1А2А3А4 середины первых трёх сторон отмечены точками В1, В2, В3.Отметим середину четвёртой стороны А1А4 точкой С (рис. 5).
Если последовательно соединить эти середины сторон четырёхугольника А1А2А3А4 (точки В1, В2, В3, С), то получится параллелограмм В1В2В3С. Если раньше эта задача (о последовательном соединении середин четырёхугольника) не решалась, то это легко доказать сейчас, что полученная фигура есть параллелограмм. Диагональ А2А4 разбивает четырёхугольник на два треугольника. В2В3 есть средняя линия треугольникаА2А3А4, и поэтому она параллельна диагонали А2А4 и равна её половине. Аналогично, В1С параллельна той же диагонали и равна её половине. Следовательно противоположные стороны В2В3 и В1C четырёхугольника В1В2В3С В1 параллельны и равны. Поэтому четырёхугольник В1В2В3С В1 – параллелограмм.
В этом параллелограмме В1В3 и В2С являются диагоналями, а они в точке пересечения делятся пополам. Отсюда следует, что точка М (середина диагонали В1В2) должна совпадать с точкой пересечения диагоналей параллелограмма, а поэтому М есть и середина диагонали В2С. А точка N есть середина В2В4. Тогда MN – средняя линия треугольника СВ2В4. Отсюда следует, что MN = 0,5СВ4. А СВ4 – средняя линия треугольника А1А4А5, поэтому СВ4 = 0,5 А1А5 = 0,5а. MN = 0,25а.
II.4. Моделирование в процессах решения задач
В науке широко используется метод моделирования. Заключается он в том, что для исследования какого-то объекта или явления выбирают или строят другой объект, в каком-то отношении подобный исследуемому. Построенный или выбранный объект изучают и сего помощью решают исследовательские задачи, а затем результаты решения этих задач переносят на первоначальное явление или объект. В процессе решения многих задач широко используется моделирование этих задач. Покажем на примере:
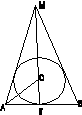
Объём конуса в 2 раза больше объёма, вписанного в него шара. Найти угол между образующей и плоскостью основания конуса.
Решение: Построим схематическую запись задачи – модель конуса. Для этого проведём сечение конуса с вписанным в него шаром плоскостью, проходящей через ось конуса. В сечении получим равнобедренный треугольник с вписанной в него окружностью (рис. 6). Т.к. боковая сторона этого треугольника есть образующая конуса, а высота треугольника есть ось конуса, перпендикулярная к плоскости основания, то угол между боковой стороной и основанием треугольника есть искомый угол между образующей и плоскостью основания.
Дано: АВМ – осевое сечение конуса; АМ = ВМ; МК┴АВ; окружность (О,ОК) – осевое сечение шара; Vк:Vш = 2.
По известным формулам Найдём объёмы конуса и шара:
Выразим все отрезки, входящие в равенство (1), через угол x отрезок АК = y.
Из треугольника АМК находим: МК = АК tgytgx. (2)
Из треугольника АОК находим: ОК = АК tg
Подставим найденные выражения их (2) и (3) в (1):
у 2 ·уtgx:( ytgx/2) 3 = 2, получаем: tgx = 8 tg 3 x/2.
2.Если же разбить сложную задачи разбить на подзадачи не удаётся, то надо, если можно, преобразовать её в более простой, в более знакомый вид.
3.Если же не удаётся, не разбить задачу на подзадачи, не преобразовать в более простой вид её, то надо ввести какие-либо вспомогательные элементы, с тем, чтобы получить задачу, которую можно разбить на подзадачи, или же преобразовать в более простой вид.
Александров Л. Д. Геометрия 6-8. М.: Просвещение, 1982.
Атанасян Л.С. Геометрия 7-9. М.: Просвещение, 1996.
Атанасян Л.С. Геометрия 10-11. М. Просвещение, 2002.
Погорелов А.В. Геометрия 7-9. М.: Просвещение, 1996.
Медяник А. И. Учителю о школьном курсе планиметрии. М.: Просвещение, 1984.
Дышинский Е.А Геометрия треугольника и окружности. Пермь,1993.
Корешкова Т.А. Математика. Тренировочные задания. М.: Просвещение. Эксмо, 2006.
Денищева Л.О., Безрукова Г.К., Бойченко Е.М. ЕГЭ: математика: 2004 – 2005. М.: Просвещение, 2005.
Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи. М.: Просвещение, 1984.
Калягин Ю.М., Оганесян В.А. Учись решать задачи. М.: Просвещение, 1984.
Никольская И.Л., Семёнов Е.Е. Учимся рассуждать и доказывать. М.: Просвещение, 1989.