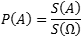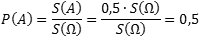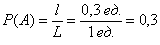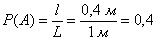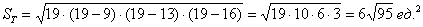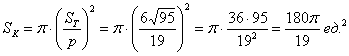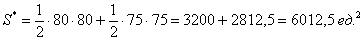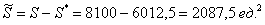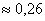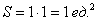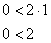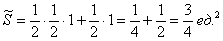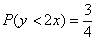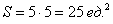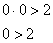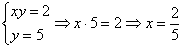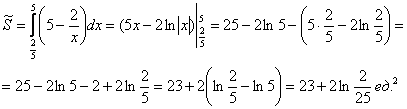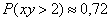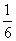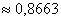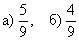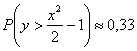Что такое геометрическая вероятность

17.04.202226.04.2022 admin 0 Comments

Геометрическая вероятность

Однако, далеко не всегда исходный набор Ω (т.е. пространство всех элементарных событий) является конечным. Например, в качестве Ω можно взять ограниченное множество точек на плоскости или отрезок на прямой.

В качестве события A можно рассмотреть любую подобласть области Ω. Например, фигуру внутри исходной фигуры на плоскости или отрезок, лежащий внутри исходного отрезка на прямой.

Заметим, что элементарным событием на таком множестве может быть только точка. В самом деле, если множество содержит более одной точки, его можно разбить на два непустых подмножества. Следовательно, такое множество уже неэлементарно.

Теперь определим вероятность. Тут тоже все легко: вероятность «попадания» в каждую конкретную точку равна нулю. Иначе получим бесконечную сумму одинаковых положительных слагаемых (ведь элементарные события равновероятны), которые в сумме по-любому больше P (Ω) = 1.

Итак, элементарные события для бесконечных областей Ω — это отдельные точки, причем вероятность «попадания» в любую из них равна нулю. Но как искать вероятность неэлементарного события, которое, подобно Ω, содержит бесконечное множество точек? Вот мы и пришли к определению геометрической вероятности.

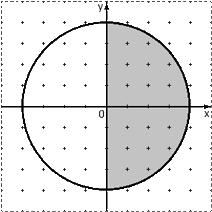
Задача. Мишень имеет форму окружности радиуса 4. Какова вероятность попадания в ее правую половину, если попадание в любую точку мишени равновероятно? При этом промахи мимо мишени исключены.

Взглянем на картинку: нас устроит любая точка из правого полукруга. Очевидно, площадь S ( A ) этого полукруга составляет ровно половину площади всего круга, поэтому имеем:

Как видите, ничего сложного в геометрической вероятности нет. Однако даже в Москве многие репетиторы по высшей математике стараются обойти эту тему стороной, поскольку считают ее необязательной. Результат — непонимание материала и, как следствие, проблемы на экзамене по теории вероятностей.

Чтобы наглядно представить себе, что такое геометрическая вероятность, возьмите лист бумаги и начертите произвольную фигуру. Треугольник, квадрат или окружность — что угодно. Затем возьмите острый, хорошо заточенный карандаш и ткните им в любую точку фигуры. Повторите этот нехитрый процесс несколько раз. Если исключить попадания за пределами фигуры, то получится вот что:

Этот опыт показывает, что конечная сумма нулевых слагаемых всегда равна нулю. Но что происходит, когда слагаемых становится бесконечно много? Здесь ситуация не так однозначна, и возможны три варианта:

Почему так происходит? Механизм возникновения положительных чисел и бесконечностей связан с понятием счетности множества. Кроме того, надо понимать, что такое мера Лебега. Впрочем, эти знания действительно нужны вам, только если вы учитесь на математика.

Источник

Геометрическое определение вероятности. Задачи с решениями

За окном ранние осенние деньки, и жёлтая листва на деревьях навевает лирическое и немного грустное настроение…. Но впереди ещё целый учебный год и в такие моменты нужно обязательно настроиться на плодотворную работу! Спешу обрадовать всех хандрящих читателей своим фирменным рецептом, позволяющим быстро повысить тонус своего организма. Для этого достаточно немножко вспомнить геометрию… …нет, я согласен, что иногда она усыпляет, но в небольших дозах – исключительно бодрит! И, главное, очень действенно – как только начинаешь принимать живительные порции знаний, так сразу никакой сезонной депрессии!

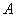
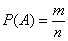
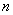
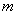
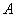
Ещё на первом уроке по теме мы познакомились с классическим определением вероятности появления некоторого события в испытании и простейшей формулой , где – общее число всех возможных равновозможных, элементарных исходов данного испытания, а – кол-во элементарных исходов, благоприятствующих событию .

Возникли затруднения с терминологией и/или пониманием? Пожалуйста, начните с основ теории вероятностей.

Едем дальше: классическое определение вероятности оказывается эффективным для решения целого спектра задач, но с другой стороны, обладает и рядом недостатков. Даже правильнее сказать, не недостатков, а ограничений. Одним из таких ограничений является тот факт, что оно неприменимо к испытаниям с бесконечным количеством исходов. Простейший пример:

На отрезок 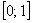наудачу бросается ~~голодная~~ точка. Какова вероятность того, что она попадёт в промежуток ?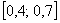

Поскольку на отрезке бесконечно много точек, то здесь нельзя применить формулу 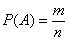(ввиду бесконечно большого значения «эн») и поэтому на помощь приходит другой подход, называемый геометрическим определением вероятности.

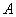
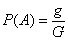
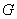
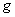
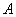
Всё очень похоже: вероятность наступления некоторого события в испытании равна отношению , где – геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а – мера, выражающая количество благоприятствующих событию исходов. На практике в качестве такой геометрической меры чаще всего выступает длина или площадь, реже – объём.

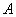
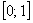
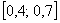
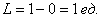
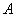
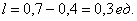
Рассмотрим событие: – брошенная на отрезок точка, попала в промежуток . Очевидно, что общее число исходов выражается длиной бОльшего отрезка: , а благоприятствующие событию исходы – длиной вложенного отрезка: По геометрическому определению вероятности:

Слишком просто? Как и в случае с классическим определением, это обманчивое впечатление. Обстоятельно и добросовестно разбираемся в практических примерах:

Метровую ленту случайным образом разрезают ножницами. Найти вероятность того, что длина обрезка составит не менее 80 см.

Решение: «чего тут сложного? Вероятность равна 1/5-й». Это автоматическая ошибка, которую допускают по небрежности. Да, совершенно верно – длина обрезка составит не менее 80 см, если от ленты отрезать не более 20 сантиметров. Но здесь часто забывают, что искомый разрез можно сделать как с одного конца ленты, так и с другого: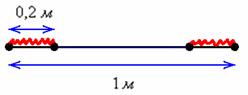

Рассмотрим событие: 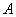– длина обрезка составит не менее 0,8 м.

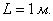
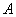
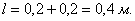
Поскольку ленту можно разрезать где угодно, то общему числу исходов соответствует её длина: Благоприятствующие событию участки разреза отмечены на рисунке красным цветом и их суммарная длина равна: По геометрическому определению:

Ответ: 0,4

Какой можно сделать вывод? Даже если задача кажется вам очень простой, НЕ СПЕШИТЕ. Импульсивность вообще штука скверная – это ошибки, ненужные покупки, испорченные ~~кожные покровы~~ отношения и т.д.… но не будем о грустном!

При оформлении задач следует обязательно указывать размерность (единицы, метры, квадратные единицы, квадратные метры и т.д.). Кстати, обратите внимание, что на финальном этапе вычислений геометрическая мера сокращается. Так в рассмотренном примере, сократились метры: 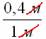, в результате чего получилась привычная безразмерная вероятность.

Разминочная задача из сборника Рябушко:

После бури на участке между 40-м и 70-м километрами телефонной линии произошёл обрыв провода. Какова вероятность того, что он произошёл между 50-м и 55-м километрами линии?

Краткое и решение и ответ в конце урока.

Значительно чаще встречаются примеры, в которых фигурируют площади:

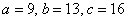
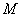
В треугольник со сторонами вписан круг. Точка произвольно ставится в треугольник. Найти вероятность того, что точка попадёт в круг.

Напоминаю, что вписанный круг лежит внутри треугольника и касается его сторон в 3 точках

Решение: поскольку точка ставится в треугольник, а круг лежит внутри, то общему числу исходов соответствует площадь треугольника, а множеству благоприятствующих исходов – площадь вписанного круга. Что тут сказать? Ищем площади:

Если даны длины сторон треугольника, то его площадь удобно найти по формуле Герона: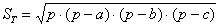
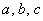
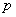
, где – длины сторон треугольника, а – полупериметр.

Сначала вычислим полупериметр треугольника: 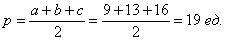, а затем его площадь:

Методику вынесения множителей из-под корня я освещал ещё в древние-древние времена на вводном уроке по аналитической геометрии.

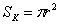
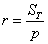
Площадь вписанного круга найдём по формуле , где – его радиус.

Откуда брать геометрические формулы? Нужные формулы можно найти в школьном учебнике или другом источнике информации. При этом нет никакой необходимости специально их разучивать, лично я вспомнил только 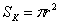, а всё остальное в считанные минуты нашёл в Википедии. И через считанные минуты всё это благополучно забуду =)

Итак, площадь вписанного круга:

По геометрическому определению:
– вероятность того, что точка попадёт во вписанный круг.

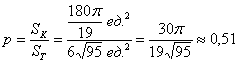
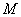
Ответ:

Более простой пример для самостоятельного решения:

В круге радиуса 10 см находится прямоугольный треугольник с катетами 12 и 7 см. В круг наудачу ставится точка. Найти вероятность того, что она не попадёт в данный треугольник.

Следует отметить, что в этой задаче треугольник вовсе не обязан как-то касаться окружности, он просто расположен внутри круга и всё. Будьте внимательны!

А теперь рассмотрим широко известную задачу о встрече:

Две грузовые машины могут подойти на погрузку в промежуток времени от 19.00 до 20.30. Погрузка первой машины длится 10 минут, второй – 15 минут. Какова вероятность того, что одной машине придется ждать окончания погрузки другой?

Давайте немного осмыслим условие. Во-первых, автомобили могут подойти на погрузку в любом порядке, а во-вторых – в любые моменты времени в течение полутора часов. По первой оглядке решение представляется довольно трудным. И для неподготовленного человека оно действительно окажется «не по зубам». Подробный анализ метода решения этой задачи можно найти, например, в учебном пособии Гмурмана, я же ограничусь в известной степени формальным алгоритмом:

Решение: сначала выясняем длительность временнОго промежутка, на котором может состояться встреча. В данном случае, как уже отмечено выше, это полтора часа или 90 минут. При этом здесь не имеют особого значения фактические временнЫе рамки – погрузка автомобилей, может состояться, например, утром с 8.30 до 10.00, и решение будет точно таким же.

Вычисления допустимо проводить как в долях часа, так и в минутах. На мой взгляд, в большинстве случаев удобнее работать с минутами – меньше путаницы.

На первом шаге изобразим прямоугольную систему координат, где в подходящем масштабе построим квадрат размером 90 на 90 единиц; при этом одна из вершин квадрата совпадает с началом координат, а его смежные стороны лежат на координатных осях.

Общему множеству исходов будет соответствовать площадь данного квадрата: 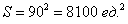Размерность лучше указать в квадратных единицах, поскольку квадратные минуты смотрятся как-то неудачно.

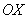
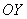
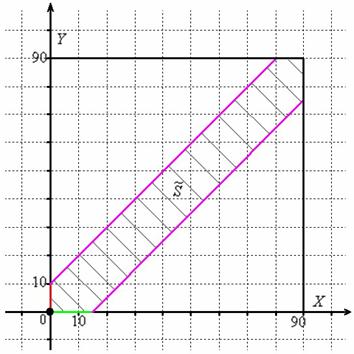
Далее по оси от начала координат откладываем время погрузки одного автомобиля (зелёная линия), а по оси – время погрузки другого автомобиля (красная линия) (можно наоборот, это не повлияет на решение):

Теперь из правого конца зелёного отрезка и из верхнего конца красного отрезка под углом 45 градусов проводим две линии внутри квадрата (малиновые отрезки).

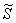
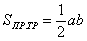
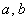
Множеству благоприятствующих исходов (когда автомобили «пересекутся» во времени) соответствует площадь заштрихованной фигуры. В принципе, её можно вычислить «на пальцах», но технически проще найти площади двух прямоугольных треугольников с помощью формулы , где – длины катетов. Обратите внимание, что в общем случае эти треугольники не равны. У нас: верхний треугольник имеет катеты длиной по 80 единиц, нижний треугольник – по 75 единиц. Таким образом, суммарная площадь треугольников составляет:

И бесхитростный заключительный манёвр: из площади квадрата вычитаем площади треугольников, получая тем самым благоприятствующую площадь:

По геометрическому определению:
– вероятность того, что одной машине придется ждать окончания погрузки другой.

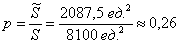
Ответ:

Если в разобранной задаче встреча была явно нежелательна, то в следующей – скорее, наоборот =) Романтичный эпизод для самостоятельного изучения:

Студенты случайным образом приходят в столовую с 14.00 до 15.00, при этом обед каждого из них занимает примерно 20 минут. Найти вероятность того, что: а) Коля встретится с Олей во время обеда, б) данная встреча не состоится.

Не нужно печалиться по поводу пункта «бэ» – любовь приходит и уходит, а кушать хочется всегда! …прошу прощения за тонкий юмор =) Решение, чертёж и ответ в конце урока.

Оставшиеся примеры статьи посвящены не менее распространённой задаче на геометрическое определение вероятности. Для начала заманивающий пример:

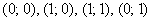
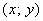
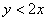
В квадрат с вершинами наудачу брошена точка . Найдите вероятность того, что координаты этой точки удовлетворяют неравенству.

Решение: изобразим на чертеже искомый квадрат и прямую :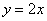

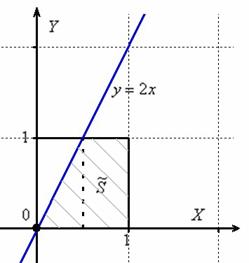
Общему множеству исходов соответствует площадь квадрата

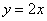
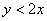
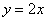
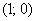
Прямая делит квадрат на треугольник и трапецию. Как определить фигуру, которая удовлетворяет условию ? Вспоминаем линейные неравенства: нужно взять любую точку, не принадлежащую прямой , например, точку и подставить её координаты в неравенство:

Получено верное неравенство, значит, множеству благоприятствующих исходов соответствует площадь 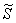трапеции. Рассчитаем данную площадь как сумму площадей прямоугольного треугольника и прямоугольника:

По геометрическому определению:
– вероятность того, что координаты брошенной в данный квадрат точки удовлетворяют неравенству.

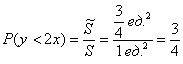
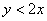
Ответ:

…я так и знал, что вы соскучились по неравенствам =) А они бывают не только линейными:

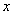
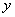
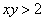
Загадываются два числа и в промежутке от 0 до 5. Какова вероятность, что ?

Схема решения уже знакома: коль скоро загадываются 2 произвольных числа от нуля до пяти (они могут быть и иррациональными), то общему количеству исходов соответствует площадь квадрата

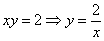
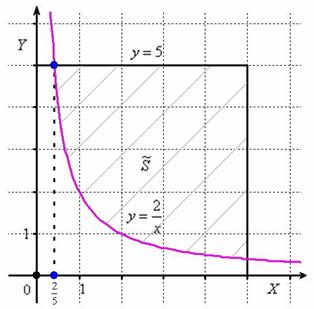
Изобразим ветвь гиперболы , которая делит квадрат на две части:

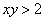
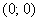
Теперь выясним, какой из этих двух «кусков» удовлетворяет неравенству . Для этого выберем любую точку, не принадлежащую гиперболе, проще всего взять , и подставим её координаты в наше неравенство:

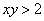
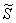
Получено неверное неравенство, а значит, условию соответствует «верхний кусок», площадь которого вычислим с помощью определённого интеграла.

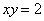
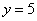
Уточним нижний предел интегрирования аналитически (найдём точку пересечения гиперболы и прямой ):

На отрезке прямая расположена не ниже гиперболы ,
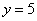
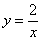
по соответствующей формуле:

По геометрическому определению:
– вероятность того, что произведение двух загаданных в промежутке от 0 до 5 чисел окажется больше двух.

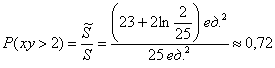
Ответ:

Аналогичный пример для самостоятельного решения:

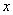
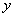
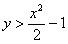
Загадываются два числа и в промежутке от 0 до 10. Какова вероятность, что ?

Данная задача (как, собственно, и предыдущая) допускает несколько способов расчёта площади, подумайте, какой путь более рационален. Моя версия решения совсем близко.

В заключение следует отметить, что геометрическое определение вероятности тоже обладает своими недостатками. Один из них заключается в своеобразном парадоксе, давайте вспомним демонстрационный пример с отрезком 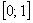, на который случайным образом падает точка. Возможно ли, что точка попадёт, например, на самый край отрезка? Да, такое событие возможно, но по геометрическому определению, его вероятность равна нулю! И то же самое можно сказать о любой точке отрезка! Дело в том, что с позиций геометрии размеры отдельно взятой точки равны нулю, и поэтому геометрическое определение вероятности здесь не срабатывает.

Надеюсь, ваше настроение значительно улучшилось и теперь вы обязательно справитесь со всеми учебными и внеучебными трудностями. …Не улучшилось?! Дополнительные задачи по теме можно найти в архиве готовых решений по сборнику Чудесенко =) =)

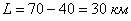
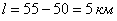
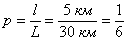
Задача 2: Решение: используем геометрическое определение вероятности. Общему числу исходов соответствует участок длиной , благоприятствующему количеству исходов – участок длиной . Таким образом:
– вероятность того, что обрыв провода произошёл между 50-м и 55-м километрами линии.
Ответ:

Задача 4: Решение: общему количеству исходов соответствует площадь круга:

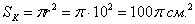
Площадь прямоугольного треугольника равна полупроизведению его катетов: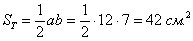

По условию поставленная в круг точка не должна попасть в треугольник, поэтому благоприятствующее число исходов выражается разностью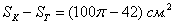
По геометрическому определению:
– вероятность того, что поставленная в круг точка не попадёт в треугольник.
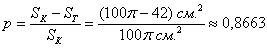
Ответ:

Задача 6: Решение: Оля и Коля могут встретиться в течение 60 минут. Выполним чертёж: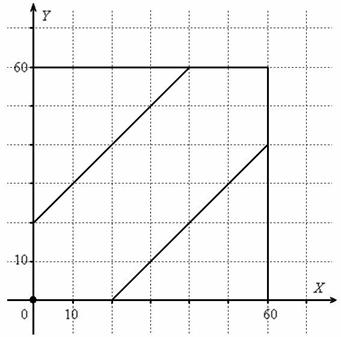

Площадь квадрата 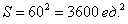соответствует общему числу исходов.
Рассмотрим противоположные события:
– Оля и Коля встретятся во время обеда;
– данной встречи не состоится.
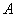
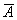
Вычислим суммарную площадь двух треугольников:
– данное значение благоприятствует событию .
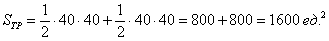
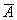
По геометрическому определению вероятности: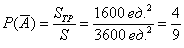

Противоположные события образуют полную группу, поэтому: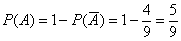

Ответ:

Задача 9: Решение: выполним чертёж: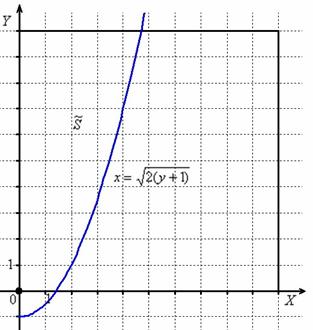

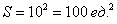
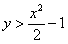
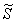
Общее число исходов выражается площадью квадрата . Неравенству соответствует площадь , которую вычислим с помощью определённого интеграла, интегрируя по «игрек» (данный метод рассмотрен в статье Объем тела вращения).
Выразим обратную функцию: .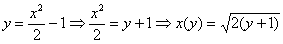
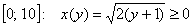
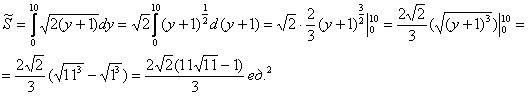
На отрезке , поэтому:

По геометрическому определению:
– вероятность того, что два загаданных от нуля до 10 числа будут удовлетворять неравенству
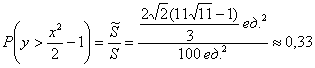
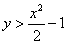
Ответ: