Что такое двусвязный список

Алгоритмы и структуры данных для начинающих: связный список

Первая структура данных, которую мы рассмотрим — связный список. На то есть две причины: первое — связный список используется практически везде — от ОС до игр, и второе — на его основе строится множество других структур данных.

Связный список

Основное назначение связного списка — предоставление механизма для хранения и доступа к произвольному количеству данных. Как следует из названия, это достигается связыванием данных вместе в список.

Прежде чем мы перейдем к рассмотрению связного списка, давайте вспомним, как хранятся данные в массиве.

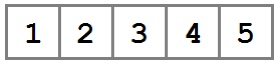
Как показано на рисунке, данные в массиве хранятся в непрерывном участке памяти, разделенном на ячейки определенного размера. Доступ к данным в ячейках осуществляется по ссылке на их расположение — индексу.

27–29 декабря, Онлайн, Беcплатно

Это отличный способ хранить данные. Большинство языков программирования позволяют так или иначе выделить память в виде массива и оперировать его содержимым. Последовательное хранение данных увеличивает производительность (data locality), позволяет легко итерироваться по содержимому и получать доступ к произвольному элементу по индексу.

Тем не менее, иногда массив — не самая подходящая структура.

Предположим, что у нашей программы следующие требования:

Поскольку в требованиях указано, что считанные числа передаются в метод ProcessItems за один раз, очевидным решение будет массив целых чисел:

У этого решения есть ряд проблем, но самая очевидная из них — что случится, если будет необходимо прочесть больше 20 значений? В данной реализации значения с 21 и далее просто проигнорируются. Можно выделить больше памяти — 200 или 2000 элементов. Можно дать пользователю возможность выбрать размер массива. Или выделить память под новый массив большего размера при заполнении старого и скопировать элементы. Но все эти решения усложняют код и бесполезно тратят память.

Нам нужна коллекция, которая позволяет добавить произвольное число элементов и перебрать их в порядке добавления. Размер коллекции должен быть неограничен, а произвольный доступ нам не нужен. Нам нужен связный список.

Прежде чем перейти к его реализации, давайте посмотрим на то, как могло бы выглядеть решение нашей задачи.

Обратите внимание: проблем, присущих первому варианту решения больше нет — мы не можем выделить недостаточно или, наоборот, слишком много памяти под массив.

Кроме того, из этого кода можно увидеть, что наш список будет принимать параметр типа и реализовывать интерфейс IEnumerable

Реализация класса LinkedList

Класс Node

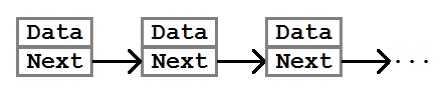
В основе связного списка лежит понятие узла, или элемента (Node). Узел — это контейнер, который позволяет хранить данные и получать следующий узел.

В самом простом случае класс Node можно реализовать так:

Класс LinkedList

Прежде чем реализовывать наш связный список, нужно понять, как мы будем с ним работать.

Ранее мы увидели, что коллекция должна поддерживать любой тип данных, а значит, нам нужно реализовать обобщенный интерфейс.

Учитывая все вышесказанное, давайте набросаем примерный план класса, а затем заполним недостающие методы.

Метод Add

Добавление элемента в связный список производится в три этапа:

Основная сложность заключается в том, чтобы найти последний узел списка. Можно сделать это двумя способами. Первый — сохранять указатель на первый узел списка и перебирать узлы, пока не дойдем до последнего. В этом случае нам не требуется сохранять указатель на последний узел, что позволяет использовать меньше памяти (в зависимости от размера указателя на вашей платформе), но требует прохода по всему списку при каждом добавлении узла. Это значит, что метод Add займет O(n) времени.

Второй метод заключается в сохранении указателя на последний узел списка, и тогда при добавлении нового узла мы поменяем указатель так, чтобы он указывал на новый узел. Этот способ предпочтительней, поскольку выполняется за O(1) времени.

Первое, что нам необходимо сделать — добавить два приватных поля в класс LinkedList : ссылки на первый (head) и последний (tail) узлы.

Теперь мы можем добавить метод, который выполняет три необходимых шага.

Метод Remove

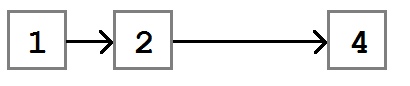
После удаления узла поле Next узла со значением «2» будет указывать на узел со значением «4».

Основной алгоритм удаления элемента такой:

Как всегда, основная проблема кроется в мелочах. Вот некоторые из случаев, которые необходимо предусмотреть:

Поле Count декрементируется при удалении узла.

Метод Contains

Метод GetEnumerator

Метод Clear

Метод CopyTo

Метод CopyTo проходит по списку и копирует элементы в массив с помощью присваивания. Клиент, вызывающий метод должен убедиться, что массив имеет достаточный размер для того, чтобы вместить все элементы списка.

Метод Count

Метод IsReadOnly

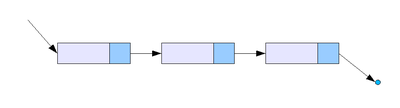
Двусвязный список

Связный список, который мы только что создали, называется также «односвязным». Это значит, что между узлами только одна связь в единственном направлении от первого узла к последнему. Есть также достаточно распространенный вариант списка, который предоставляет доступ к обоим концам — двусвязный список.

Далее мы рассмотрим только отличия в реализации односвязного и двусвязного списка.

Класс Node

Единственное изменение, которое надо внести в класс LinkedListNode — добавить поле со ссылкой на предыдущий узел.

Метод AddFirst

При добавлении элемента в начало списка последовательность действий примерно такая же, как и при добавлении элемента в односвязный список.

Метод AddLast

Метод RemoveFirst

Метод RemoveLast

Метод Remove

Зачем нужен двусвязный список?

Так мы сможем итерироваться по списку вручную, в том числе от последнего элемента к первому.

В этом примере мы используем поля Tail и Previous для того, чтобы обойти список задом наперед.

Кроме того, двусвязный список позволяет легко реализовать двусвязную очередь, которая, в свою очередь, является строительным блоком для других структур данных. Мы вернемся к ней позже, в соответствующей части.

Продолжение следует

На этом мы заканчиваем разбор связных списков. В следующий раз мы подробно разберем массивы.

Источник

Двусвязный линейный список

Каждый узел двунаправленного (двусвязного) линейного списка (ДЛС) содержит два поля указателей — на следующий и на предыдущий узлы. Указатель на предыдущий узел корня списка содержит нулевое значение. Указатель на следующий узел последнего узла также содержит нулевое значение.

Узел ДЛС можно представить в виде структуры:

Основные действия, производимые над узлами ДЛС:

Инициализация ДЛС

Инициализация списка предназначена для создания корневого узла списка, у которого поля указателей на следующий и предыдущий узлы содержат нулевое значение.

Добавление узла в ДЛС

Функция добавления узла в список принимает два аргумента:

Процедуру добавления узла можно отобразить следующей схемой:

Добавление узла в ДЛС включает в себя следующие этапы:

Таким образом, функция добавления узла в ДЛС имеет вид:

Возвращаемым значением функции является адрес добавленного узла.

Удаление узла ДЛС

В качестве аргументов функции удаления узла ДЛС передается указатель на удаляемый узел. Поскольку узел списка имеет поле указателя на предыдущий узел, нет необходимости передавать указатель на корень списка.

Функция возвращает указатель на узел, следующий за удаляемым.

Удаление узла может быть представлено следующей схемой:

Удаление узла ДЛС включает в себя следующие этапы:

Удаление корня ДЛС

Функция удаления корня ДЛС в качестве аргумента получает указатель на текущий корень списка. Возвращаемым значением будет новый корень списка — тот узел, на который указывает удаляемый корень.

Вывод элементов ДЛС

Функция вывода элементов ДЛС аналогична функции для ОЛС.
В качестве аргумента в функцию вывода элементов передается указатель на корень списка.
Функция осуществляет последовательный обход всех узлов с выводом их значений.

Для ДЛС также можно вызвать функцию вывода элементов списка в обратном порядке.

Вывод элементов ДЛС в обратном порядке

Функция вывода элементов ДЛС в обратном порядке принимает в качестве аргумента указатель на корень списка. Функция перемещает указатель на последний узел списка и осуществляет последовательный обход всех узлов с выводом их значений в обратном порядке.

Взаимообмен узлов ДЛС

В качестве аргументов функция взаимообмена узлов ДЛС принимает два указателя на обмениваемые узлы, а также указатель на корень списка. Функция возвращает адрес корневого узла списка.

Взаимообмен узлов списка осуществляется путем переустановки указателей. Для этого необходимо определить предшествующий и последующий узлы для каждого заменяемого. При этом возможны две ситуации:

При замене соседних узлов переустановка указателей выглядит следующим образом:

При замене узлов, не являющихся соседними переустановка указателей выглядит следующим образом:

Функция взаимообмена узлов списка выглядит следующим образом:

Источник

Двусвязный список

Двусвязный список

Каким образом можно упростить удаление последнего элемента? Очевидно, что если бы мы хранили указатель на предыдущий элемент, то было бы возможно удалять последний.

Для реализации списка нам понадобится структура узел

Указатель prev хранит адрес предыдущего узла, если его нет (значит, это первый узел) то переменная равна NULL. Аналогично, указатель next хранит адрес следующего узла. Структура «Двусвязный Список» будет хранить свой размер (чтобы не пересчитывать количество элементов каждый раз), а также указатель head, ссылающийся на первый элемент, и указатель tail, ссылающийся на последний элемент

В случае, когда в списке нет элементов, оба они равны нулю. Если в списке один элемент, то оба указателя ссылаются на один и тот же элемент (соответственное, они равны). Об этом постоянно следует помнить: каждый раз, удаляя или вставляя элемент, придётся проверять, чтобы указатели head и tail правильно хранили адреса.

Первая функция, как обычно, создаёт экземпляр структуры DblLinkedList

В ней нет ничего интересного. Заодно опишем функцию, которая удаляет список

Теперь, определим набор стандартных функций – pushFront и popFront для работы с головой, pushBack И popBack для работы с последним элементом, getNth, insert и deleteNth для вставки и удаления в произвольное место.

Вставка спереди очень похожа на вставку в односвязный список. Сначала создаётся новый элемент

потом задаём ему значения

Так как он стал первым, то указатель next ссылается на старую голову списка, а предыдущего элемента нет. Теперь, если в списке уже был головной элемент, то его указатель prev должен ссылаться на вновь созданный элемент

Теперь проверим указатель tail. Если он пустой, то после добавления нового элемента он должен ссылаться на него

Теперь перекинем указатель head на вновь созданный элемент и увеличим значение счётчика size

Удаление из начала списка также похоже на оное для односвязного списка. Прибавляются только перекидывания дополнительных указателей и проверка, чтобы указатель на последний элемент, в случае, если элементов больше не осталось, стал равным нулю.

Сначала создадим указатель на первый элемент списка. Он понадобится, чтобы после изменения всех указателей prev и next мы смогли удалить узел.

После этого перекинем указатель head на следующий за ним элемент

Далее проверяем, что удаляемы элемент не является одновременно последним (когда в списке всего один элемент), после чего освобождаем память.

Получение n-го элемента очень простое и не отличается от оного для односвязного списка.

Можно улучшить эту функцию: если список длинный, то в зависимости от индекса можно проходить либо с начала в конец, либо с конца в начало. Это позволяет всегда использовать не более N/2 шагов.

Теперь можно написать функцию удаления и вставки узла. Сначала находим нужный элемент, затем создаём либо новый узел (если вставка), либо указатель на удаляемый элемент. Затем изменяем все указатели.

Не забываем, конечно, смотреть за значениями head И tail, чтобы они указывали на существующие в данный момент элементы.

В примерах будем использовать переменные типа int

Вторая функция – создание списка из массива

Теперь можно пользоваться двусвязным списком

Сортировка вставками

Теперь непосредственно сортировка

Видно, что в конце в переданном списке не остаётся элементов, так как мы их выталкиваем, так что старый список мы подменяем на вновь созданный.

Сложность алгоритма – O(n 2 ), мы имеем одни проход по неотсортированному списку сложностью порядка n, для каждого элемента проходим по отсортированному.

Так как при каждом создании нового узла мы удаляем узел из первого списка, то дополнительной памяти не требуется.

Тепер сравним сложности различных операций для односвязного и двусвязного списка. Однонаправленный связный список

Источник

Двусвязный список

В информатике, cвя́зный спи́сок — структура данных, состоящая из узлов, каждый из которых содержит как собственные данные, так и одну или две ссылки («связки») на следующее и/или предыдущее поле. Принципиальным преимуществом перед массивом является структурная гибкость: порядок элементов связного списка может не совпадать с порядком расположения элементов данных в памяти компьютера, а порядок обхода списка всегда явно задаётся его внутренними связями.

Содержание

Виды связных списков

Линейный связный список

Односвязный список

В односвязном списке можно передвигаться только в сторону конца списка. Узнать адрес предыдущего элемента из данного невозможно.

Двусвязный список

По двусвязному списку можно передвигаться в любом направлении — как к началу, так и к концу. В этом списке проще производить удаление и перестановку элементов, т.к. всегда известны адреса тех элементов списка, указатели которых направлены на изменяемый элемент.

XOR-связный список

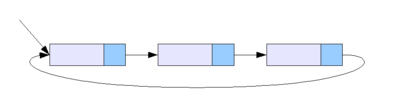
Кольцевой связный список

Разновидностью связных списков является кольцевой (циклический, замкнутый) список. Он тоже может быть односвязным или двусвязным. Последний элемент кольцевого списка содержит указатель на первый, а первый (в случае двусвязного списка) — на последний.

Список с пропусками

Развёрнутый связный список

Достоинства

Недостатки

См. также

Полезное

Смотреть что такое «Двусвязный список» в других словарях:

Связный список — В информатике, связный список базовая динамическая структура данных, состоящая из узлов, каждый из которых содержит как собственно данные, так и одну или две ссылки («связки») на следующий и/или предыдущий узел списка.[1] Принципиальным… … Википедия

Односвязный список — В информатике, cвязный список структура данных, состоящая из узлов, каждый из которых содержит как собственные данные, так и одну или две ссылки («связки») на следующее и/или предыдущее поле. Принципиальным преимуществом перед массивом является… … Википедия

Связанный список — В информатике, cвязный список структура данных, состоящая из узлов, каждый из которых содержит как собственные данные, так и одну или две ссылки («связки») на следующее и/или предыдущее поле. Принципиальным преимуществом перед массивом является… … Википедия

XOR-связный список — структура данных, похожая на обычный двусвязный список, однако в каждом элементе хранящая только один адрес результат выполнения операции XOR над адресами предыдущего и следующего элементов списка. Для того, чтобы перемещаться по списку,… … Википедия

Развёрнутый связный список — список, каждый физический элемент которого содержит несколько логических (обычно в виде массива, что … Википедия

Xor-связанный список — XOR связный список структура данных, похожая на обычный двусвязный список, однако в каждом элементе хранящая только один адрес результат выполнения операции XOR над адресами предыдущего и следующего элементов списка. Для того, чтобы перемещаться… … Википедия

Структура данных — Бинарное дерево, простой пример ветвящейся связной структуры данных. Структура данных (англ. data structure) программная единица, позволяющая хран … Википедия

Коллекция (программирование) — У этого термина существуют и другие значения, см. Коллекция. Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные исто … Википедия

Коллекция данных — Коллекция в программировании программный объект, содержащий в себе, тем или иным образом, набор значений одного или различных типов, и позволяющий обращаться к этим значениям. Коллекция позволяет записывать в себя значения и извлекать их.… … Википедия

Двусвязная очередь — (жарг. дэк, дек от англ. deque double ended queue; двухсторонняя очередь, двусвязный список, очередь с двумя концами) структура д … Википедия

Источник

Связный список и двусвязный список

Связный список (linked list) — это структура данных, в которой элементы линейно упорядочены, но порядок определяется не номерами элементов (как в массивах), а указателями, входящих в состав элементов списка и указывают на следующий элемент. У списка должна быть «голова» (первый элемент) и «хвост» (последний элемент).

Преимущества и недостатки по сравнению с массивами

В отличие от массивов, вставка и удаление элементов в Связный список производится за постоянное время (О (1)). Также значительным преимуществом связных списков является возможность легкого расширения: чтобы увеличить размер списка, нужно только добавить еще один элемент.

Недостатком связных списков необходимость проходить весь список, чтобы найти элемент (то есть время доступа к элементу списка = О (n)).

Элемент связанного списка (узел)

Элементы связанного списка называют узлами. Каждый узел содержит данные, которые мы хотим сохранить, а также указатель на следующий элемент в списке или NULL, если этот элемент является последним.

В коде на картинке приведен код структуры, который реализует элемент связанного списка (и собственно список). Данные представлены числовым значением.

Иными словами, мы используем синтаксис структуры для создания нашего собственного типа данных для инкапсуляции узла.

int n — это данные, которые мы хотим сохранить в узле.
struct node * next — указатель на следующий узел в связанном списке.

Помните, что узел не будет typedef-ed до тех пор, пока все эти строки не будут выполнены. Таким образом, мы должны написать узел struct вместо простого узла, как перед фигурными скобками, так и внутри фигурных скобок. В самой последней строке мы предоставляем node для typedef как имя, которое мы хотим использовать для этого нового типа данных для остальной части нашей программы.

Поиск по списку

Для поиска элемента в списке, необходимо пройти весь список. Это реализуется с помощью перехода с текущего элемента на следующий по ссылке.

В этом примере для того, чтобы найти элемент «9», необходимо прежде всего с головы списка перейти на элемент «2». Затем перейти по ссылке на элемент «3». Только после этого можно по ссылке найти элемент «9».

Ниже — код функции, которая ищет заданный элемент в списке и возвращает true, если элемент есть в списке, или false, если элемента нет в списке.

Если ptr достиг конца списка без поиска значения, которое мы ищем, функция возвращает false.

Вставка элемента в список

Существует три различных возможных варианта вставки элемента в список: вставка в начало, конец списка и вставка в любое другое место внутри списка.

Рассмотрим вставку в начало списка (так как это наиболее часто используемый вариант вставки).

Очень важно, чтобы шаги 2 и 3 были проведены именно в таком порядке. Если сначала установить head на новый элемент, мы потеряем часть списка.

Ниже приведён код функции для вставки нового элемента в начало списка:

Таким образом, для вставки в начало связанного списка нужно:

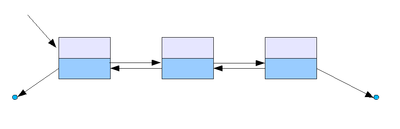
Двусвязный список

Двусвязный список похож на обычный связный список, только элементы в нем хранят ссылки не только на следующий, но и на предыдущий элемент. Благодаря этому свойству, можно перемещаться по списку вперед и назад.

Элемент двусвязного списка содержит данные и два поля: prev и next, указатели на предыдущий и следующий элементы списка соответственно.

Код структуры элемента двусвязного списка на Си:

Источник