Что такое двумерные фигуры

Двумерные фигуры и их изображение (Форма, фигура и пространство)

Содержание:

ВЕДЕНИЕ

Для того чтобы научиться верно изображать предметы с натуры на плоскости, необходимо иметь представление об их форме, объеме и конструкции. Эти сведения помогут в дальнейшем решать учебные задачи при работе над рисунком, позволят лучше понять и разобраться в строении предметных форм при изображении.

Под формой предмета следует понимать геометрическую сущность поверхности предмета, характеризующую его внешний вид. Всякий предмет или объект в природе, от микрочастиц до гигантских космических тел, имеет определенную форму, и форма человеческого тела здесь не исключение. Следовательно, любой предмет есть форма, а форма подразумевает объем.

Форма любого предмета в своей основе понимается или рассматривается как его геометрическая сущность, его внешний вид или внешние очертания.

Известный художник и педагог Д.Н. Кардовский считал, что форма есть масса, имеющая тот или иной характер подобно геометрическим телам, таким как куб, шар, цилиндр и др. Это в равной степени относится и к живым формам, которые при всей сложности имеют в основе (схеме) скрытую геометрическую сущность.

Осмысливая внешние очертания предметов, необходимо также осмыслить и сущность их внутреннего строения, конструкцию формы и связь отдельных элементов, составляющих ту или иную форму. Конструкция предмета, как правило, определяет характер его формы.

При внимательном анализе форм предметов, при всей их кажущейся сложности, в них всегда можно увидеть геометрическую конструктивную основу или сочетание нескольких таких основ, образующих эту форму.

От структуры строения предмета во многом зависят приемы построения его формы на плоскости. Поэтому, анализируя форму предмета, как бы она ни была сложна на первый взгляд, прежде всего необходимо проникнуть в сущность его внутреннего строения, не отвлекаясь на мелкие детали, мешающие понять геометрическую основу его конструкции. изобразительных задач и свободно, уверенно рисовать как с натуры, так и по воображению, что чрезвычайно важно для профессиональной творческой деятельности.

Для лучшего понимания конструкции предметов и приобретения навыков грамотного изображения их формы также необходимо вспомнить полученные в школе знания по геометрии, такие, как понятия о точках, линиях, простых и объемных фигурах.

1. Форма, фигура и пространство

Существует два способа типизации форм и фигур. Формы и фигуры могут быть двухмерными, либо трехмерными.

Двухмерная форма имеет ширину и длину. Она также может служить иллюзорным изображением трехмерных объектов. Трехмерные фигуры имеют также высоту и толщину.

Формы и фигуры также бывают органическими и геометрическими. Органические формы, такие, например, как холмы, покрытые снегом, имеют неправильную форму и часто асимметричны. Органические формы чаще всего имеют природное происхождение.

Наше восприятие фигур и форм зависит от множества факторов. Расположение точки зрения, с которой мы видим объект, может подчеркнуть или скрыть некоторые его свойства, и, следовательно, снизить или повысить эффект, который он производит на смотрящего.

Рассмотрим предмет с точки зрения изучения геометрической информации, которая в нем заключена.

Геометрическая информация представляет собой совокупность данных о геометрической форме предмета, положении и ориентации его в пространстве.

Каждый предмет имеет свою форму, которая является его основной визуальной характеристикой.

Геометрической формой называется внешний облик предмета, характеризующийся совокупностью его геометрических свойств.

К геометрическим свойствам предметов относятся: размеры, пропорции, взаимное расположение составляющих элементов формы.

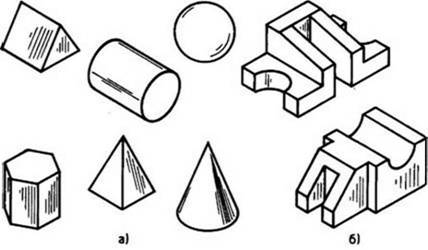
Предметы бывают простой и сложной формы (см. Рисунок 1).

К предметам простой формы относятся те, которые представляют собой геометрические тела: цилиндр, конус, шар, призма, пирамида (Рисунок 1, а). К предметам сложной (составной) формы относятся такие, которые образованы сочетанием различных геометрических тел (Рисунок 1, б).

В процессе выполнения рисунка переводят объемную форму предмета в плоскостное изображение. При этом необходимо определить, как преобразуется видимая форма предмета при плоскостном изображении, какие части и элементы предмета изменяются, какие будут видимыми и т.д. Правильность решения этой задачи зависит от умения наблюдать и знания законов построения аксонометрии [1].

Необходимо разобраться в общей форме предмета и правильно понять ее. Для облегчения этой задачи можно применить способ обобщения (упрощения формы). Суть его заключается в том, что любую сложную форму рассматривают как сочетание простейших геометрических форм. Такой способ построения помогает правильно понять и изобразить трехмерный объемный предмет, развивает пространственное представление и облегчает работу.

Приступая к изучению изображаемого предмета, необходимо установить:

— из каких главных простейших составляющих элементов (шар, цилиндр, призма, пирамида, конус и др.) составлена натура;

— взаимное расположение выявленных фигур относительно друг друга;

— пропорциональные соотношения размеров фигур, а также расстояние между ними.

2. Виды двухмерных фигур

Планиметрия Планиме́трия (от лат. planum — «плоскость», др.-греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости: треугольники, окружности, параллелограммы и т.д.

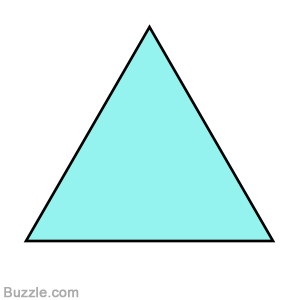
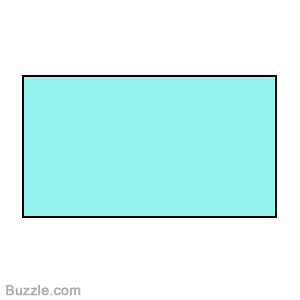
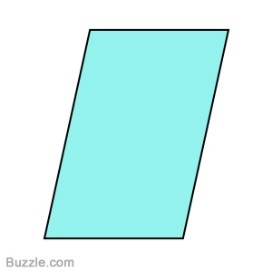
Двухмерные фигуры (2D): многоугольник (разновидности многоугольников: треугольник, четырёхугольник (разновидности четырёхугольника: параллелограмм, прямоугольник, ромб, квадрат, трапеция, дельтоид), пятиугольник, шестиугольник и т. д. до бесконечности); окружность, круг, круговой сегмент, круговой сектор, эллипс, овал и т.д. (см. Рисунок 2).

Рисунок 2 – Виды двухмерных фигур

Формы двухмерных фигур, представленных на Рисунке 2, являются основными, в категории 2D геометрии, которые являются простейшими составляющими фигур и предметов объемной формы (3D).

Для того, чтобы передать объемность изображаемых предметов, нужно провести конструктивный анализ их формы, что позволит мысленно вписать их в простейшие геометрические тела. Важно научиться правильно строить наиболее часто встречающиеся трехмерные геометрические формы[2].

Когда в рисунке передана конструктивная основа формы изображаемого предмета, остается только перейти к изображению деталей, характерных особенностей и мелких подробностей. При всем разнообразии объемных тел их можно условно разделить на три основные группы: граненной, круглой и комбинированной форм, а некоторые из наиболее простых трехмерных геометрических форм, поверхность состоит из плоских многоугольников.

3. Построение аксонометрических проекций двухмерных фигур

3.1 Виды аксонометрических проекций

Чертеж дает точное представление о форме и размерах предмета, но часто уступает в наглядности обычному художественному рисунку, и недостаточно квалифицированный технический работник не всегда способе правильно понять общий облик изделия, представленного в виде чертежных проекций. В этих случаях, для улучшения наглядности чертежа, применяют дополнительные изображения предмета (изделия) в виде аксонометрических проекций.

Следует отметить, что аксонометрические проекции, применяемые в черчении, не являются художественным рисунком предмета, поскольку выполняются без соблюдения перспективы, т. е. методом параллельного проецирования, тогда как художник использует центральное проецирование и не придерживается строгих масштабов изображения.

Аксонометрические проекции делятся на прямоугольные и косоугольные. В первом случае проецирующие лучи перпендикулярны аксонометрической плоскости проекции; при этом форма предмета и его размеры передаются без искажений.

Во втором случае проецирующие лучи не перпендикулярны аксонометрической плоскости проецирования, при этом размеры и форма предмета передаются с искажениями.

К прямоугольным аксонометрическим проекциям относятся изометрическая и диметрическая проекции. Именно эти способы объемного изображения чертежей применяются наиболее часто [2].

Косоугольные проекции практически не используются в техническом черчении, поскольку они малоинформативны (не передают должным образом размеры и форму предмета).

Стандартами ЕСКД предусматривается изометрические проекции (не искажается ни один из основных размеров), диметрические проекции (искажается лишь один или два размера) и триметрические проекции (искажены все размеры предмета). Триметрические проекции относятся к косоугольным [5].

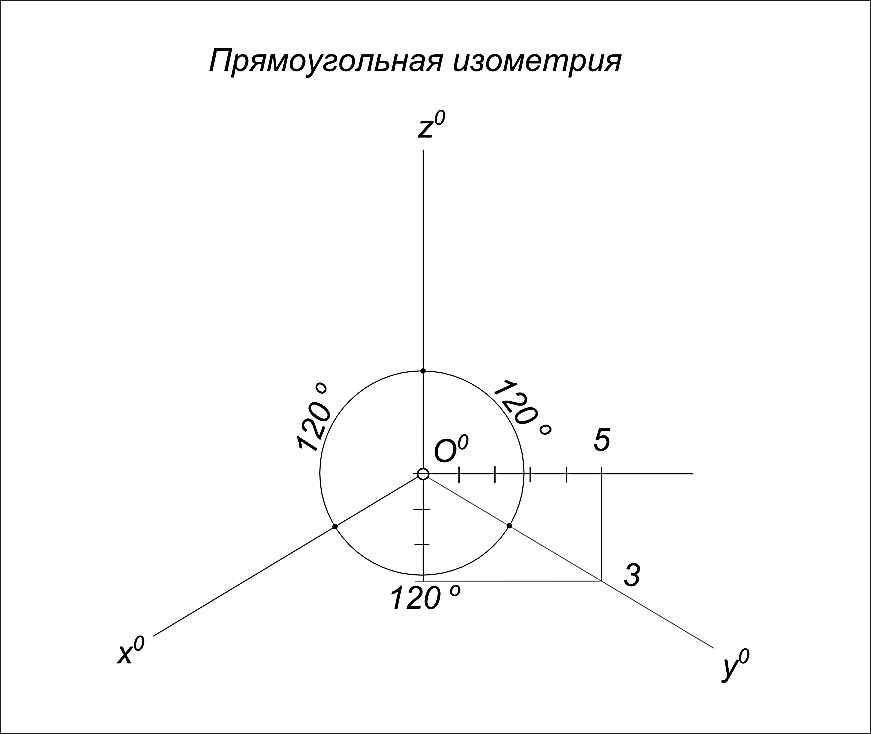
Прямоугольная изометрическая проекция представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным плоскости аксонометрических проекций, и с одинаковыми по трем аксонометрическим осям коэффициентами искажения, равными 0,82.

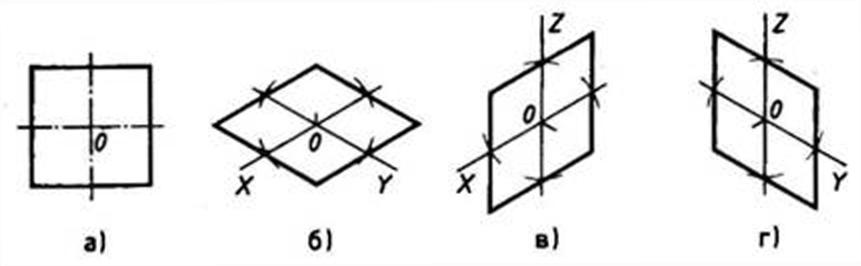
Оси изометрической проекции (Рисунок 3) составляют между собой углы, равные 120°. Ось Z располагают вертикально, тогда оси ХР и Yp составят с горизонтальной прямой углы в 30° (Рисунок 3).

При построении изометрической проекции все линейные размеры предмета, параллельные осям координат, надо умножать на коэффициент 0,82, т. е. уменьшать их по сравнению с действительными размерами. Однако на практике коэффициенты искажения округляют до единицы, что позволяет значительно упростить построения. Изометрические проекции, построенные с учетом теоретических или округленных коэффициентов искажения, отличаются друг от друга только размером, так как в первом случае масштаб изображения 1:1, а во втором — 1,22: 1 (110,82=1,22).

Рисунок 3 – Оси прямоугольной изометрии

Прямоугольную изометрическую проекцию применяют довольно широко благодаря простоте построения ее осей и одинаковому соотношению осей эллипсов — проекций окружностей, расположенных в плоскостях проекций или плоскостях, им параллельных.

Однако нужно иметь в виду, что изометрическая проекция, построенная с округленными коэффициентами искажения, получается увеличенной и чем крупнее изображаемый предмет, тем более заметна разница между нормальной и увеличенной изометрической проекцией. Поэтому изометрическую проекцию крупных предметов следует строить с учетом коэффициентов искажения или помещать на отдельном формате.

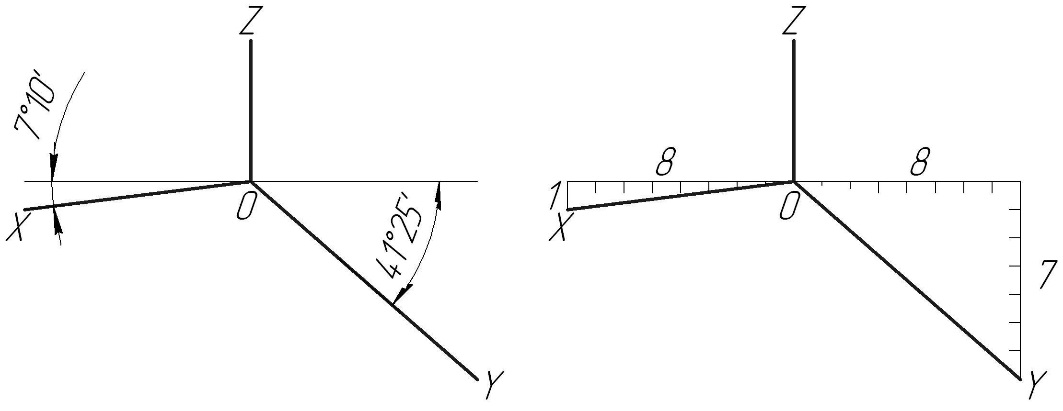
Прямоугольная диметрическая проекция представляет собой аксонометрическую проекцию с равными показателями искажения по двум осям. По ГОСТу 2.317- 2011 принята прямоугольная диметрия с равными показателями искажения по осям Х и Z. В стандарте предусмотрено упрощение, заключающееся в том, что по осям Х и Z, или параллельно им откладываются действительные величины отрезков, а по направлению оси Y коэффициент искажения равен 0,5.

Рисунок 4 – Расположение осей в диметрии

Изображение фигуры в диметрии получают, как и в изометрии увеличенным, причём увеличение по каждой оси равно 1,06.

Фронтальная диметрическая проекция относится к косоугольным аксонометрическим проекциям, так как ее получают с помощью проецирующих прямых, не перпендикулярных плоскости аксонометрических проекций.

Для построения фронтальной диметрической проекции оси прямоугольных координат X и Z располагают параллельно плоскости Р, поэтому коэффициенты искажения по осям Х и Z равны единице.

Направление проецирования выбирают так, чтобы коэффициент искажения по оси Y был равен 0,5. Оси Х и Z взаимно перпендикулярны, а ось Y составляет с ними углы, равные 135°. При построении фронтальной диметрической проекции отрезки, параллельные осям координат X и Z, сохраняют свою величину, а отрезки, параллельные оси У, уменьшают в два раза [2].

При построении фронтальной диметрической проекции фигуры, расположенные во фронтальной плоскости или плоскости ей параллельной, не искажаются. Поэтому этот вид аксонометрической проекции рекомендуется использовать в тех случаях, когда целесообразно получить истинный вид плоской фигуры.

Фронтальная диметрическая проекция также удобна для изображения предметов, имеющих в своих очертаниях окружности или криволинейные контуры, расположенные во фронтальной плоскости или в плоскостях ей параллельных[3].

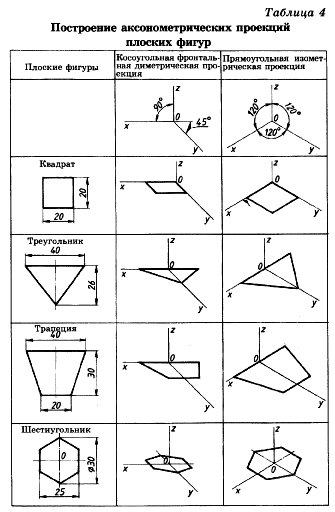
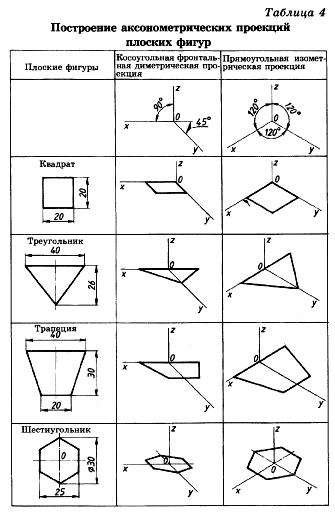
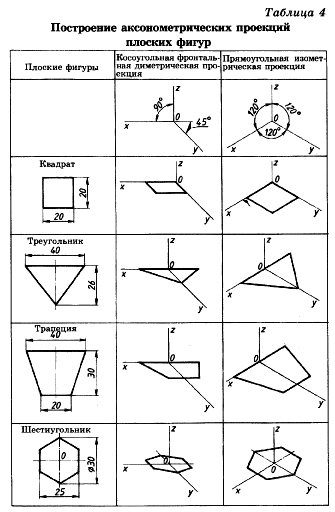
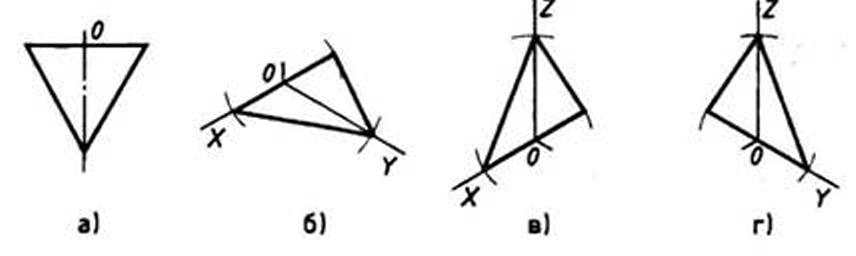
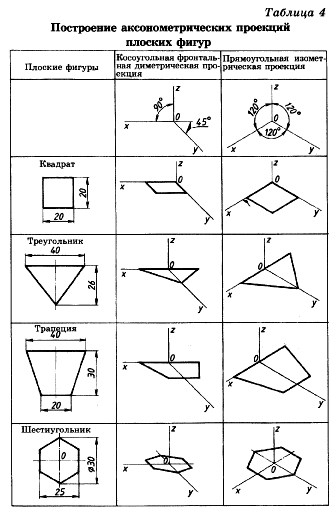
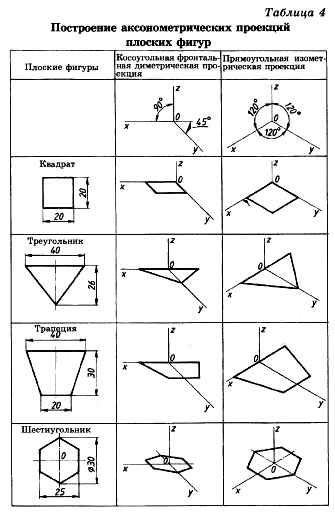
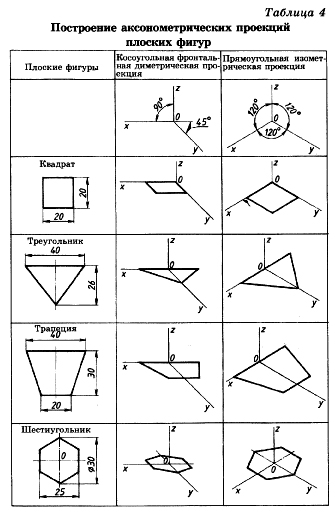
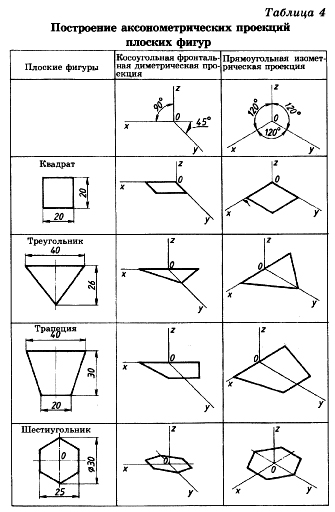
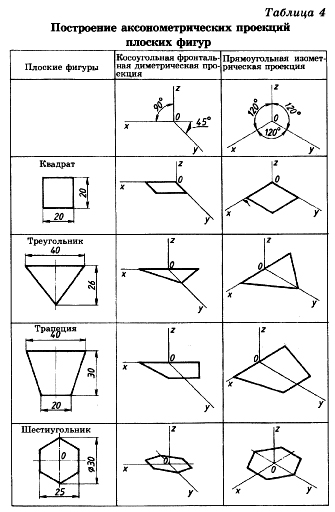
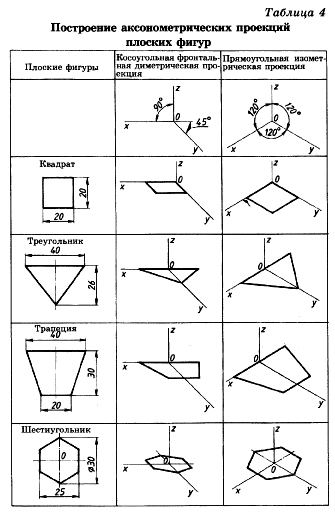
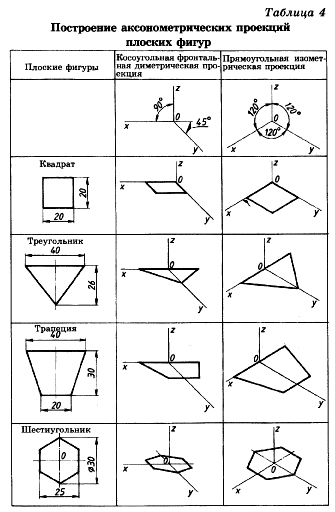
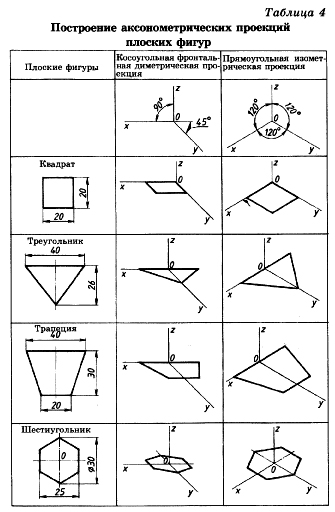
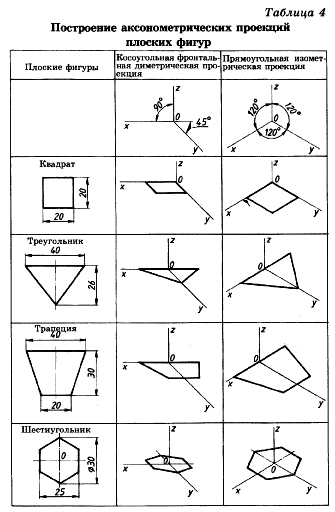
3.2 Построение аксонометрических проекций треугольника

Продолжим луч х за точку начала координат (т. О).

От точки О по обе стороны на оси х откладываем отрезки, равные половине стороны треугольника, получив тем самым изображение стороны треугольника.

По оси у во фронтальной диметрической проекции откладываем половину высоты треугольника (26×0,5=13 мм), а в изометрической проекции по оси у откладываем размер, равный высоте треугольника (26 мм). Полученные засечки соединяем отрезками прямых, получая аксонометрические изображения треугольника.

Косоугольная фронтальная диаметрическая проекция

Прямоугольная изометрическая проекция

3.3 Построение аксонометрических проекций квадрата

При построении изометрической проекции квадрата из точки О по аксонометрическим осям х и у откладывают длины стороны квадрата. Через полученные засечки проводят прямые, параллельные осям.

Косоугольная фронтальная диаметрическая проекция

Прямоугольная изометрическая проекция

3.4 Построение аксонометрических проекций трапеции

Продолжим луч х за центр координат (т. О). От точки О по обе стороны на оси х откладываем отрезки, равные половине верхнего основания трапеции (по 20 мм).

Во фронтальной диметрической проекции по оси у откладываем половину высоты трапеции (15 мм), а в изометрической проекции по той же оси откладываем отрезок, равный высоте трапеции. Через полученные засечки проводим отрезки прямых, параллельные оси х. На них по обе стороны от оси откладываем отрезки, равные половине нижнего основания трапеции.

Полученные проекции вершин трапеции соединяем последовательно между собой и получаем аксонометрические проекции трапеции

Косоугольная фронтальная диаметрическая проекция

Прямоугольная изометрическая проекция

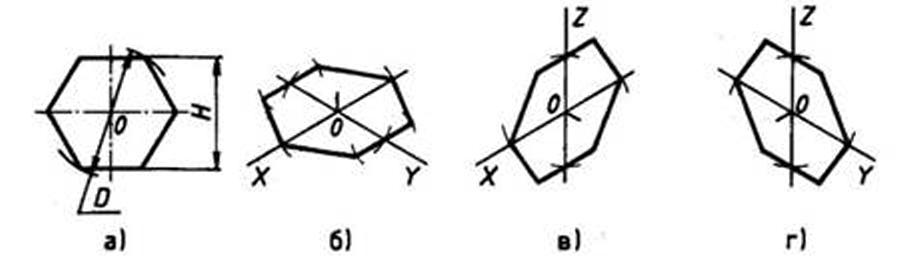
3.5 Построение аксонометрических проекций шестиугольника

От точки О в обе стороны по оси х откладываем отрезки, равные 25:2=12,5 мм.

Через полученные засечки проводим прямые, параллельные оси у, и на них от оси х на прямых, параллельных оси у, откладываем отрезки, равные 1/4 стороны шестиугольника для фронтальной диметрической проекции и 1/2 стороны шестиугольника для прямоугольной изометрической проекции. Таким образом мы найдем четыре проекции вершин, принадлежащих шестиугольнику.

По оси у от точки О во фронтальной диметрической проекции откладываем половину радиуса описанной окружности, а для изометрической проекции — величину К (радиус описанной окружности), получая еще две проекции вершин. Построенные проекции вершин последовательно соединяем, получая аксонометрическое изображение шестиугольника [5].

Косоугольная фронтальная диаметрическая проекция

Прямоугольная изометрическая проекция

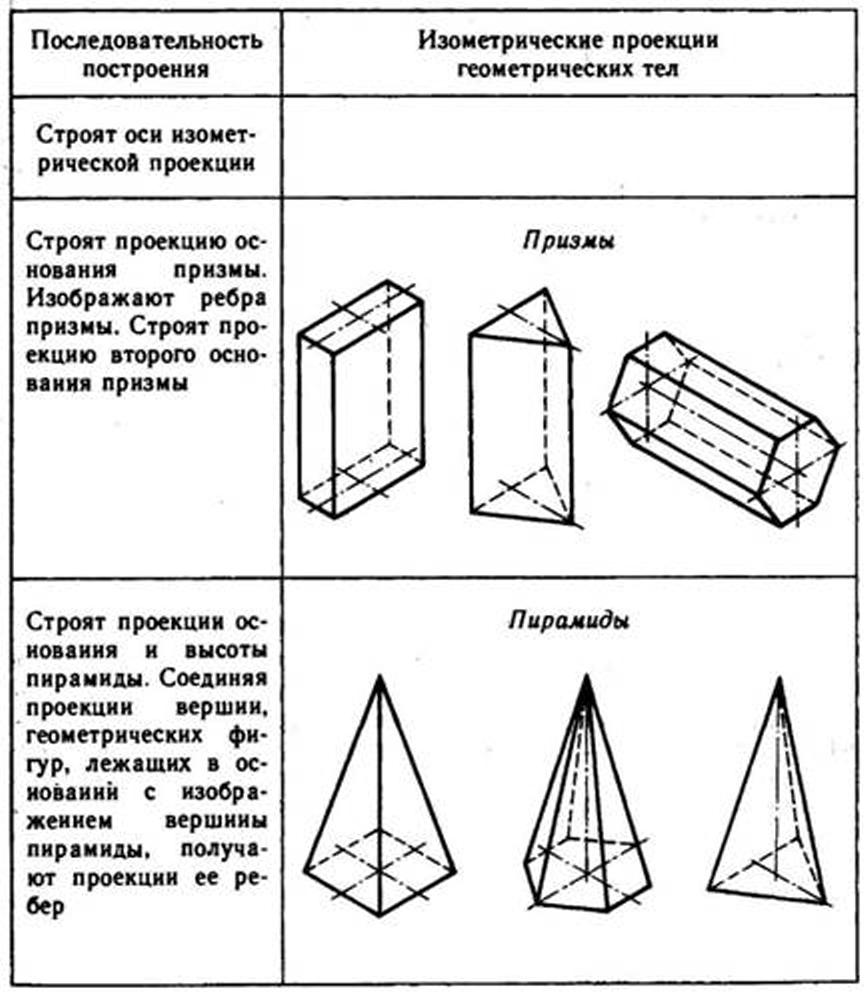
Таблица 1 Изометрические проекции простых геометрических тел (основание: треугольник, шестигранник, квадрат)

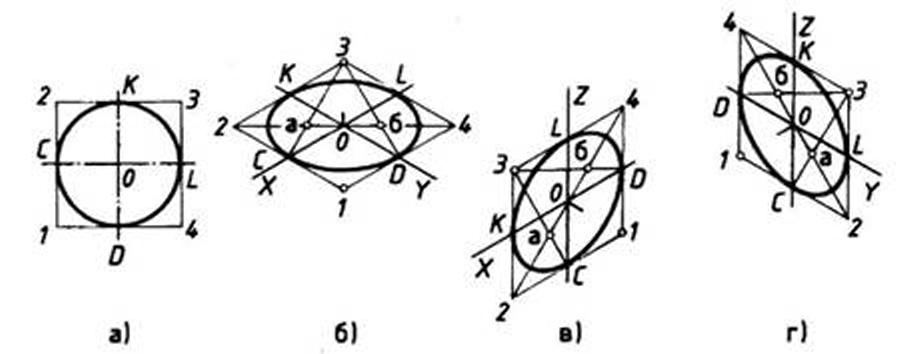
3.6 Построении аксонометрических проекции круга

При построении изометрической проекции круга из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, параллельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D.

В пересечениях прямых получаются центры: а и б малых дуг, проведя которые получают овал, заменяющий аксонометрическую проекцию круга[4].

Рисунок 8— Прямоугольная и изометрические проекции круга

Используя описанные построения двухмерных фигур, можно выполнить аксонометрические проекции простых геометрических тел (Таблица 1, 2).

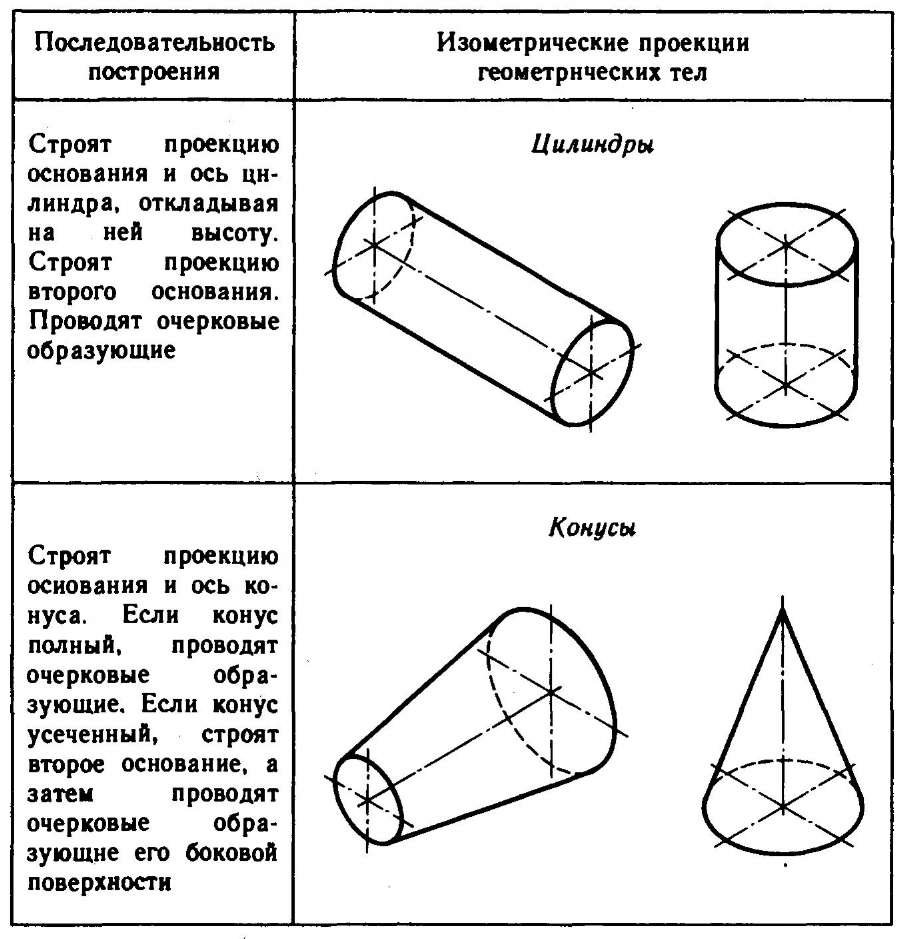
Таблица 2 Изометрические проекции простых геометрических тел (основание – круг)

ЗАКЛЮЧЕНИЕ

В целях упрощения построения рисунка предмета следует располагать изображение так, чтобы его основные измерения были параллельны аксонометрическим осям. Это позволяет строить изображение, откладывая размеры (или координаты) по направлениям соответствующих осей с учетом коэффициентов искажения. Изображая симметричные предметы, целесообразно одну из аксонометрических осей совмещать с осью симметрии предмета.

В процессе выполнения рисунка переводят объемную форму предмета в плоскостное изображение. При этом необходимо определить, как преобразуется видимая форма предмета при плоскостном изображении, какие части и элементы предмета изменяются, какие будут видимыми и т.д.

Правильность решения этой задачи зависит от умения наблюдать и знания законов построения аксонометрии. Для выполнения изометрической проекции любой детали не­обходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Необходимо разобраться в общей форме предмета и правильно понять ее. Для облегчения этой задачи можно применить способ обобщения (упрощения формы). Суть его заключается в том, что любую сложную форму рассматривают как простейшую геометрическую. Такой способ построения помогает правильно понять и изобразить трехмерный объемный предмет, развивает пространственное представление и облегчает работу.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

Интернет ресурсы:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Двумерное пространство

Двуме́рное простра́нство (иногда говорят двухме́рное пространство) — геометрическая модель плоской проекции физического мира, в котором мы живём. Двумерным пространством считается n-мерное пространство, где n=2.

Содержание

Геометрия двумерного пространства

Многогранники

В двумерном пространстве существует бесконечно много правильных многогранников: правильные многоугольники. Примеры последних приведены ниже:

Выпуклые

Название	Треугольник (2-симплекс)	Квадрат (2-куб)	Пятиугольник	Шестиугольник	Семиугольник	Восьмиугольник
Символ Шлефли
Вид
Название	Девятиугольник	Десятиугольник	11-угольник	12-угольник	13-угольник	14-уольник
Символ Шлефли
Вид
Название	15-угольник	16-угольник	17-угольник	18-угольник	19-угольник	20-угольник	. n-угольник
Символ Шлефли							<n>
Вид

Гиперсфера

Гиперсферой в двумерном пространстве является окружность, которую иногда называют 1-сфера, потому что её поверхность является одномерной. Площадь части плоскости, заключённой внутри гиперсферы (площадь круга) равна:

,

где — радиус окружности.

Системы координат в двумерном пространстве

Наиболее распространённые координатные системы — прямоугольная (Декартова) система координат, полярная система координат и географическая координатная система.

Примечания

См. также

Размерность пространства
Пространство	Одномерное • Двумерное • Трёхмерное • Четырёхмерное • Пятимерное (англ.) • Шестимерное (англ.) • Семимерное (англ.) • Восьмимерное (англ.) • n-мерное • Пространство-время • Проективное пространство
Политопы и фигуры	Симплекс • Гиперкуб • Гиперпрямоугольник (ортотоп) (англ.) • Полугиперкуб (англ.) • Кросс-политоп (англ.) • Гиперсфера
Концепции	Прямоугольная система координат • Линейная алгебра • Геометрическая алгебра (англ.) • Conformal geometry • Плоскость поворота (англ.) • Пространство • Дробная размерность (Размерность Минковского, размерность Хаусдорфа) • Мультивселенная • Многообразие
Математика

Полезное

Смотреть что такое «Двумерное пространство» в других словарях:

ДВУМЕРНОЕ МНОГООБРАЗИЕ ОГРАНИЧЕННОЙ КРИВИЗНЫ — метрическое пространство, являющееся двумерным многообразием с внутренней метрикой, для к рого определены аналоги таких понятий двумерной римановой геометрии, как длина и интегральная кривизна кривой, площадь и интегральная гауссова кривизна… … Математическая энциклопедия

ДВУМЕРНОЕ МНОГООБРАЗИЕ — топологическое пространство, каждая точка к рого обладает окрестностью, гомеоморфной плоскости или полуплоскости. Д. м. наиболее наглядный класс многообразий: к ним относятся сфера, круг, лист Мёбиуса, проективная плоскость, бутылка Клейна и др.… … Математическая энциклопедия

ПРОСТРАНСТВО — 1. Фундаментальное значение – пространство это абстракция геометрическая характеристика системы локализации m объектов в n измерениях. В классической модели физического пространства: m конечное число, а n = 3. Это так называемое Евклидово… … Толковый словарь по психологии

Пространство — (старославянск. «пространыи» широкий, просторный) 1. фундаментальное значение – абстракция, геометрическая характеристика системы локализации «m» объектов в «n» измерениях. В классической модели физического пространства «m» число объектов, а «n»… … Энциклопедический словарь по психологии и педагогике

КВАЗИЕВКЛИДОВО ПРОСТРАНСТВО — двумерное пространство, в к ром каждое направление, заданное в его точке, может быть включено в поле, направления к рого переносятся параллельно по любому пути (т. е. К. п. допускает абсолютный параллелизм). Геодезические линии К. п. распадаются… … Математическая энциклопедия

Фазовое пространство — Двумерное фазовое пространство динамической системы (её развитие имеет вид расходящейся спирали) Фазовое пространство в математике и физике … Википедия

Трёхмерное пространство — Трёхмерная метрика пространства … Википедия

Одномерное пространство — геометрическая модель материального мира, в которой положение точки возможно охарактеризовать всего одним числом.[1] Также одномерным пространством считается n мерное пространство, где n=1. Геометрия одномерного пространства Единственным… … Википедия

Источник