Что такое двумерная случайная величина
Двумерные случайные величины
| Главная > Учебные материалы > Математика: Двумерные случайные величины | ||
 | ||
 | ||
| 1.Двумерная случайная величина. 2.Плотность вероятности двумерной случайной величины. | ||
1.Двумерная случайная величина.
Функция распределения одной случайной величины не может описать все многообразие природных и, в том числе, экономических процессов и явлений. Для описания этих процессов используются двумерные и многомерные случайные величины. В данной главе остановимся на двумерных случайных величинах.
Двумерной случайной величиной называется функция вероятного события, наступившего в результате принятия величинами х и y случайных значений.
X и Y случайные величины, которые могут быть как дискретными, так и непрерывными.
Двумерную случайную величину можно интерпретировать как случайно взятую точку на плоскости Оxy, где x и y координаты этой точки.(Рис.1) Т.е. функция распределения F (x,y) есть вероятность попадания случайной точки в квадрант с вершиной в точке А(x,y), лежащей левее и ниже этой точки.
Для дискретной случайной величины функция распределения имеет следующий вид:
где вероятность суммируется для всех x i i Рис.1
Свойства функции распределения двумерной случайной величины.
1.Функция 0 ≤ F(x,y) ≤ 1, т.е. величина неотрицательная меньше 1.
2.Функция F(x,y) есть возрастающая функция по каждому из аргументов.
3.Функция распределения F(x,y) = 0, если хотя бы один из аргументов x или y стремится к минус бесконечности.
4.Функция F(x,y) равна функции от одного аргумента F(x) (F(y)), если y (x) стремится к бесконечности.
5. Функция F(x,y) равна 1, если оба аргумента стремятся к плюс бесконечности.
Геометрический смысл функции распределения есть поверхность на координатной плоскости Оxy.(Рис.2) Значение функции равно вероятности попадания случайной величины в область, рассчитанную по формуле:
Формула рассчета вероятности, состоящая из 4-х слагаемых, объясняется тем, что вероятность равна вероятности попадания случайной величины в бесконечный квадрант, исходящий из точки В, минус квадрант в точках А и С и плюс бесконечный квадрант в точке D, т.к. квадрант в точке D был вычтен дважды.
2.Плотность вероятности двумерной случайной величины.
Как известно, случайная величина имеет плотность вероятности, если она непрерывна. Говоря о случайных величинах, двумерная случайная величина называется непрерывной, если ее функция распределения является непрерывной функцией. И существует вторая смешанная производная F » xy (x,y), которая и является плотностью вероятности двумерной случайной величины.
Т.е. плотность вероятности это вторая смешанная производная от функции распределения двумерной случайной величины:
В общем виде плотность вероятности двумерной случайной величины выражается следующей формулой:
Если случайные величины подчинены нормальному закону распределения и не коррелированы (r = 0 ), то формула плотности вероятности примет вид:
Вероятность попадания непрерывной двумерной случайной величины в область D равна:
Функция распределения непрерывной двумерной случайной величины имеет вид:
Пример 1
Двумерная дискретная случайная величина
Ранее мы разобрали примеры решений задач для одномерной дискретной случайной величины. Но бывает, что результат испытания описывается не одной, а несколькими случайными величинами (случайным вектором).
Система двух случайных величин: теория
Двумерная ДСВ задается законом распределения (обычно представленным в виде таблицы распределения):
По нему можно найти одномерные законы распределения (составляющих):
$$P(X=x_i, Y=y_k)=P(X=x_i)\cdot P(Y=y_k),$$
Если случайные величины зависимы, для них можно выписать условные законы распределения (для независимых они совпадают с безусловными законами):
Далее вы найдете разные примеры задач с полным решением, где используются дискретные двумерные случайные величины (системы случайных величин).
Примеры решений
Задача 2. Два баскетболиста по два раза бросают мяч в корзину. При каждом броске вероятность попадания для первого баскетболиста 0,6, для второго – 0,7. Случайная величина X – число попаданий первым баскетболистом по кольцу. Случайная величина Y – суммарное число попаданий обоими баскетболистами. Построить таблицу распределения случайного вектора (X,Y). Найти характеристики вектора (X,Y). Зависимы или независимы случайные величины X и Y.
Задача 3. Слово РОССИЯ разрезано по буквам. Случайным образом вынимаем две буквы, тогда X – количество гласных среди них, затем вынимаем еще две буквы и Y – количество гласных во второй паре. Составить закон распределения системы случайных величин X, Y.
Задача 6. Бросаются две одинаковые игральные кости. Случайная величина X равна 1, если сумма выпавших чисел четна, и равна 0 в противном случае. Случайная величина Y равна 1, если произведение выпавших чисел четно, и 0 в противном случае. Описать закон распределения случайного вектора (X,Y). Найти D[X], D[Y] и cov[X,Y].
Задача 8. Для заданного закона распределения вероятностей двухмерной случайной величины (Х, Y):
Y\X 2 5
8 0,15 0,10
10 0,22 0,23
12 0,10 0,20
Найти коэффициент корреляции между величинами Х и Y.
Задача 9. Задана дискретная двумерная случайная величина (X,Y).
А) найти безусловные законы распределения составляющих;
Б) построить регрессию случайной величины Y на X;
В) построить регрессию случайной величины X на Y;
Г) найти коэффициент ковариации;
Д) найти коэффициент корреляции.
20 30 40 50 70
3 0,01 0,01 0,02 0,02 0,01
4 0,04 0,3 0,06 0,03 0,01
5 0,02 0,03 0,06 0,07 0,05
9 0,05 0,03 0,04 0,02 0,03
10 0,03 0,02 0,01 0,01 0,02
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
ДВУМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Двумерной называют случайную величину (Х, Y), возможные значения которой есть пары чисел (х, у). Составляющие Х и Y, рассматриваемые одновременно, образуют систему двух случайных величин.
Двумерную величину геометрически можно истолковать как случайную точку М(Х, Y) на плоскости хОу, либо как случайный вектор 
Функция распределения двумерной случайной величины (Х, Y) определяется соотношением F(x; y) = P(Xх1 х2 … хi …
б) для функции нескольких случайных аргументов Y = j(Х1, Х2,…, Хn)

где Кij – корреляционный момент для случайных величин Хi и Xj , а через 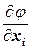
Если случайные величины взаимно не коррелированны, то 
17.1. Дискретная случайная величина имеет ряд распределения:
| x |  |  | 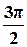 | 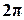 |  | |
| р | 0,1 | 0,2 | 0,1 | 0,2 | 0,3 | 0,1 |
Найти закон распределения функции z = sinx, вычислить M[Z] и D[Z].
17.2. Непрерывная случайная величина Х имеет плотность вероятности f(x). Выразить функцию распределения и плотность вероятности случайной величины Z = x 2 через функцию и плотность распределения Х.
17.3. Независимые случайные величины Х и Y распределены показательно с параметрами a и b соответственно a ¹ b. Найти плотность вероятности случайной величины Z = X + Y.
17.4. Система состоит из двух независимых элементов, соединенных последовательно в смысле надежности. Время безотказной работы каждого из элементов имеет показательное распределение с параметрами a1 и a2 соответственно. Найти функцию распределения времени безотказной работы системы.
17.5. Система состоит из двух независимых элементов, соединенных параллельно в смысле надежности. Время безотказной работы каждого из элементов имеет показательное распределение с параметрами a1 и a2 соответственно. Найти функцию распределения времени безотказной работы системы.
17.6. Непрерывная случайная величина имеет плотность 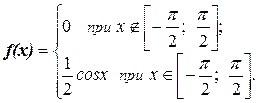
17.7. Две независимые случайные величины Х и Y имеют следующие законы распределения:
| х | y | |||||
| р | 0,2 | 0,5 | 0,3 | р | 0,4 | 0,6 |
Найти закон распределения случайной величины Z = X–2Y и проверить свойства математических ожиданий и дисперсией M[Z] = M[X]–2M[Y], D[Z] = D[X]+4D[Y].
17.9. Начальная фаза j малых свободных колебаний груза на пружине связана с начальным смещение Х, начальной скоростью v и свободной круговой частотой колебаний w формулой 



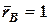

 |


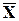


 |
 |
Указание. 
17.13. Пусть Х – непрерывная случайная величина с плотностью f(x). Выразить плотность вероятности функции z = aX+b (a > 0) через f(x).
17.14. Две независимые случайные величины Х и Y имеют следующие законы распределения:
| х | –4 | y | |||||
| р | 0,2 | 0,6 | 0,2 | р | 0,5 | 0,2 | 0,3 |
Найти закон распределения случайной величины Z = 2X–Y и проверить свойства математических ожиданий и дисперсией M[Z] = 2M[X]–M[Y], D[Z] = 4D[X]+D[Y].
17.15. Колебательная система состоит из груза с массой m = 1 кг и пружины с жесткостью k = 4 Н/м. Она выводится из состояния равновесия случайным смещением Х0, распределенным равномерно на отрезке [–0,1 м; 0,1 м] и случайным Р0 = mv0, математическое ожидание которого 

Указание. Амплитуда свободных колебаний связана с начальными условиями соотношением 
17.16. При измерении стороны квадрата линейкой, цена деления которой равно 2D, допускается погрешность округления. Пусть длина стороны квадрата равна а. Найти плотность вероятности случайной величины S – результата вычисления площади квадрата. Вычислить математическое ожидание и дисперсию S и сравнить полученные точные значения с приближенными, определенными по методу линеаризации.
Указание. Результат измерения Х есть случайная величина, равномерно распределенная на отрезке [а–D; а+D].
17.17. По сторонам прямого угла xОy концами скользит линейка АВ длины l, занимая случайное положение, причем все значения абсциссы X её конца А на оси Ох в пределах от 0 до l одинаково вероятны. Найти математическое ожидание расстояния R от начала координат до линейки.
Закон больших чисел
Под законом больших чисел понимается ряд теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
Рассмотрим вспомогательные теоремы: лемму и неравенство Чебышева, с помощью которых доказывается закон больших чисел в форме Чебышева.
Лемма Чебышева. Если случайная величина Х принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числа А верно неравенство


Неравенство Чебышева. Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо неравенство


Для некоторых случайных величин неравенство Чебышева записывается так:
a) для случайной величины X, имеющей биномиальный закон распределения с математическим ожиданием 


б) для частости 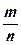


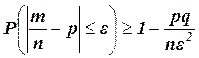
Теорема Чебышева. Если дисперсии n независимых случайных величин X1 , X2 , …, Xn ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий a1 , a2 , …, an , т.е.

Следствие. Если независимые случайные величины X1 , X2 , …, Xn имеют одинаковые математические ожидания, равные а, а их дисперсии ограничены одной и той же постоянной С, то

18.1. Среднее число вызовов, поступающих в течение часа на станцию скорой помощи, равно 30. Оценить вероятность того, что в течение часа число вызовов: а) превысит 40; б) не превысит 50.
18.2. Фонд заработной платы учреждения составляет 200 тыс. руб., а вероятность того, что зарплата случайно взятого сотрудника не превысит 1000 рублей, равна 0,6. Оценить численность персонала учреждения.
18.4. Вероятность своевременной доставки почтового отправления адресату равна 0,98. Оценить с помощью неравенства Чебышева вероятность того, что число несвоевременно доставленных среди 1000 почтовых отравлений находится в границах от 10 до 30 (включительно). Уточнить вероятность того же события с помощью интегральной теоремы Муавра-Лапласа.
18.5. Дисперсия отдельного измерения некоторой величины не превосходит 2. Сколько надо провести измерений величины, чтобы с вероятностью, не меньшей 0,95, гарантировать отклонение средней арифметической этих измерений от истинного значения величины не более чем на 0,1 (по абсолютной величине)?
18.6. На основании длительных наблюдений за спортивными достижениями легкоатлета составлена следующая таблица его результатов в беге на 100 м:
| Время, показанное спортсменом, в сек. | 10,5 | 11,5 | |||
| Вероятность | 0,1 | 0,3 | 0,5 | 0,05 | 0,05 |
С помощью леммы Чебышева оценить вероятность того, что легкоатлет на стометровке покажет время хуже 12 секунд.
18.7. Даны 50 независимых неотрицательных случайных величин Х1, Х2, …, Х50 с математическими ожиданиями М[Хi] = 0,5 и дисперсиями D[Xi] = 0,5 (i = 1, 2, …, 50). С помощью неравенства Чебышева оценить вероятность того, что средняя арифметическая этих случайных величин не превзойдет величины, равной 1.
18.8. По данным переписи населения в среднем 90% семей имеют холодильники. С помощью неравенства Чебышева оценить вероятность того, что из 1000 семей доля семей, имеющих холодильник, будет отличаться от вероятности этого события не более чем на 0,04 (по абсолютной величине).
18.9. Опрос показал, что адресная реклама в среднем в каждом пятидесятом случае приводит к тому, что потенциальный покупатель приобретает рекламируемый товар. С помощью неравенства Чебышева найти границы, в которых будет находиться число сделанных по рекламе заказов, если всего разослано 10000 рекламных листков.
18.10. Продолжительность горения электролампочки является случайной величиной, дисперсия которой не превышает 8100. Пользуясь теоремой Чебышева, оценить наибольшее отклонение средней арифметической продолжительности горения 4000 электролампочек от средней арифметической их математических ожиданий, если результат необходимо гарантировать с вероятностью, не меньшей 0,9.
18.11. Практика показывает, что 7% накладных, проходящих проверку в бухгалтерии, оказываются неправильно оформленными. Используя неравенство Чебышева, оценить вероятность того, из 500 накладных доля правильно оформленных окажется от 0,91 до 0,95.
18.12. Для определения среднего веса пакета со стиральным порошком в партии из 100 коробок было взято на выборку по одному пакету из каждой коробки. Оценить вероятность того, что средний вес отобранных 100 пакетов отличается от среднего веса пакета во всей партии не более чем на 10 г (по абсолютной величине), если известно, что среднее квадратическое отклонение веса пакета в каждой коробке меньше 18 г.
3. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Основы выборочного метода
xi – значения признака (случайной величины Х);
N и n – объемы генеральной и выборочной совокупностей;
Ni и ni – число элементов генеральной и выборочной совокупностей со значением признака хi;
Таблица 1. Расчет характеристик генеральной и выборочной совокупностей.
| Наименование характеристики | Генеральная Совокупность | Выборка |
| Средняя |  |  |
| Дисперсия |  |  |
| Доля |  |  |
Важнейшей задачей выборочного метода является оценка параметров (характеристик) генеральной совокупности по данным выборки.
Таблица 2. Оценка параметров генеральной совокупности












