Что такое дружественные числа

Дружественные числа

Дру́жественные чи́сла — два различных натуральных числа, для которых сумма всех собственных делителей первого числа равна второму числу и наоборот, сумма всех собственных делителей второго числа равна первому числу. Иногда частным случаем дружественных чисел считаются совершенные числа: каждое совершенное число дружественно себе. Большого значения для теории чисел эти пары не имеют, но являются любопытным элементом занимательной математики.

Содержание

История

Дружественные числа были открыты последователями Пифагора, которые, однако, знали только одну пару дружественных чисел — 220 и 284.

Формулу для нахождения некоторых пар дружественных чисел предложил примерно в 850 году арабский астроном и математик Сабит ибн Курра (826—901). Его формула позволила найти две новые пары дружественных чисел. Много столетий спустя Эйлер нашёл ещё 65 пар дружественных чисел. Одна из них — 17296 и 18416. Но общего способа нахождения таких пар нет до сих пор.

Неизвестно, конечно или бесконечно количество пар дружественных чисел. На сентябрь 2007 года известно 11994387 пар дружественных чисел. [1] Все они состоят из чисел одной чётности. Существует ли чётно-нечётная пара дружественных чисел, неизвестно. Также неизвестно, существуют ли взаимно простые дружественные числа, но если такая пара дружественных чисел существует, то их произведение должно быть больше .

Примеры

Ниже приведены все пары дружественных чисел, меньших 100 000.

Пары дружественных чисел образуют последовательность:

220, 284, 1184, 1210, 2620, 2924, 5020, 5564, 6232, 6368, … (последовательность A063990 в OEIS)

Способы построения

Формула Сабита

Если для натурального числа 1″ border=»0″ /> все три числа:

, , ,

являются простыми, то числа и образуют пару дружественных чисел. Эта формула даёт пары (220, 284), (17296, 18416) и (9363584, 9437056) соответственно для , но больше никаких пар дружественных чисел для не существует. Кроме того, многие дружественные числа, например (6232, 6368), не могут быть получены по этой формуле.

Метод Вальтера Боро

Если для пары дружественных чисел вида и числа и являются простыми, причём не делится на , то при всех тех натуральных , при которых оба числа и просты, числа и — дружественные.

См. также

Примечания

Ссылки

Полезное

Смотреть что такое «Дружественные числа» в других словарях:

ДРУЖЕСТВЕННЫЕ ЧИСЛА — два натуральных числа, каждое из которых равно сумме правильных делителей другого (т. е. делителей, меньших этого числа). Напр., 284 и 220 … Большой Энциклопедический словарь

ДРУЖЕСТВЕННЫЕ ЧИСЛА — ДРУЖЕСТВЕННЫЕ ЧИСЛА, два натуральных числа, каждое из которых равно сумме правильных делителей другого (т. е. делителей, меньших этого числа). Напр., 284 и 220 … Энциклопедический словарь

Дружественные числа — пара натуральных чисел, каждое из которых равно сумме всех собственных (или правильных) делителей другого, т. е. делителей, отличных от самого числа. Д. ч. 284 и 220, имеющие соответствующую сумму делителей 1+2+4+5+10+11+20+22+44+55+110 … Большая советская энциклопедия

ДРУЖЕСТВЕННЫЕ ЧИСЛА — пара натуральных чисел, каждое из к рых равно сумме собственных делителей другого, т. е. делителей, отличных от самого числа. Определение Д. ч. имеется уже в Началах Евклида, а также в трудах Платона. Древним грекам была известна одна пара Д. ч … Математическая энциклопедия

Числа Армстронга — Самовлюблённое число, или совершенный цифровой инвариант (англ. pluperfect digital invariant, PPDI) или число Армстронга натуральное число, которое в данной системе счисления равно сумме своих цифр, возведённых в степень, равную… … Википедия

Избыточные числа — Избыточное число положительное целое число n, сумма положительных собственных делителей (отличных от n) которого превышает n. Любое натуральное число относится к одному из трёх классов: избыточные числа, совершенные числа, недостаточные… … Википедия

Рецепт Вальтера Боро — Дружественные числа два натуральных числа, для которых сумма всех делителей первого числа (кроме него самого) равна второму числу и сумма всех делителей второго числа (кроме него самого) равна первому числу. Иногда частным случаем дружественных… … Википедия

МАТЕМАТИКИ ИСТОРИЯ — Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом… … Энциклопедия Кольера

Совершенное число — (др. греч. ἀριθμὸς τέλειος) натуральное число, равное сумме всех своих собственных делителей (т. е. всех положительных делителей, отличных от самого числа). По мере того как натуральные числа возрастают, совершенные числа встречаются… … Википедия

Число Армстронга — Самовлюблённое число, или совершенный цифровой инвариант (англ. pluperfect digital invariant, PPDI или число Армстронга натуральное число, которое в данной системе счисления равно сумме своих цифр, возведённых в степень, равную количеству его… … Википедия

Источник

Что такое дружественные числа

Дружественные числа — два различных натуральных числа, для которых сумма всех собственных делителей первого числа равна второму числу и наоборот, сумма всех собственных делителей второго числа равна первому числу. Иногда частным случаем дружественных чисел считаются совершенные числа: каждое совершенное число дружественно себе. Большого значения для теории чисел эти пары не имеют, но являются любопытным элементом занимательной математики.

Дружественные числа были открыты последователями Пифагора, которые, однако, знали только одну пару дружественных чисел — 220 и 284.

История

Формулу для нахождения некоторых пар дружественных чисел предложил примерно в 850 году арабский астроном и математик Сабит ибн Курра (826—901). Его формула позволила найти две новые пары дружественных чисел. Много столетий спустя Эйлер нашёл ещё 65 пар дружественных чисел. Одна из них — 17296 и 18416. Но общего способа нахождения таких пар нет до сих пор.

Неизвестно, конечно или бесконечно количество пар дружественных чисел. На сентябрь 2007 года известно 11994387 пар дружественных чисел. [1] Все они состоят из чисел одной чётности. Существует ли чётно-нечётная пара дружественных чисел, неизвестно. Также неизвестно, существуют ли взаимно простые дружественные числа, но если такая пара дружественных чисел существует, то их произведение должно быть больше .

Примеры

Ниже приведены все пары дружественных чисел, меньших 100 000.

1. 220 и 284 (Пифагор, около 500 до н. э.)

2. 1184 и 1210 (Паганини, 1860)

Пары дружественных чисел образуют последовательность:

220, 284, 1184, 1210, 2620, 2924, 5020, 5564, 6232, 6368, …

Способы построения

Формула Сабита

Если для натурального числа 1″ src=»http://upload.wikimedia.org/wikipedia/ru/math/e/b/3/eb380f3b2439960f7727e82712b46659.png» /> все три числа:

, , ,

являются простыми, то числа и образуют пару дружественных чисел. Эта формула даёт пары (220, 284), (17296, 18416) и (9363584, 9437056) соответственно для , но больше никаких пар дружественных чисел для не существует. Кроме того, многие дружественные числа, например (6232, 6368), не могут быть получены по этой формуле.

Метод Вальтера Боро

Если для пары дружественных чисел вида и числа и являются простыми, причём не делится на , то при всех тех натуральных , при которых оба числа и просты, числа и — дружественные.

Источник

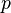
Дружественные числа

Дру́жественные чи́сла — два натуральных числа́, для которых сумма всех делителей первого числа́ (кроме него самого) равна второму числу и сумма всех делителей второго числа́ (кроме него самого) равна первому числу. Иногда частным случаем дружественных чисел считаются совершенные чи́сла: каждое совершенное число дружественно себе. Обычно же, говоря о дружественных числах, имеют в виду пары из двух разных чисел.

Дружественные числа были открыты последователями Пифагора. Правда пифагорейцы знали только одну пару дружественных чисел — 220 и 284. Только спустя много столетий Эйлер нашёл ещё 65 пар дружественных чисел. Одна из них — 17296 и 18416. Но общего способа нахождения таких пар нет до сих пор.

Формулу, дающую 3 пары дружественных чисел, открыл около 850 арабский астроном и математик Табит ибн Кура ( 826 — 901 ): если

, , ,

где 1>» /> — натуральное число, а — простые числа, то и — пара дружественных чисел. Эта формула даёт пары (220, 284), (17296, 18416) и (9363584, 9437056) соответственно для , но больше никаких пар дружественных чисел для . Кроме того, многие дружественные числа, например (6232, 6368), не могут быть получены по этой формуле S02

На ноябрь 2006 известно 11 446 960 пар дружественых чисел. Все они состоят из двух чётных или двух нечётных чисел. Есть ли чётно-нечётная пара дружественных чисел, неизвестно. Также неизвестно, существуют ли взаимно простые дружественные числа, но если такая пара дружественных чисел существует, их произведение должно быть больше .

Краткая таблица дружественных чисел

Ниже приведены все пары дружественных чисел, меньших 100 000.

Пары дружественных чисел образуют последовательность:
220, 284, 1184, 1210, 2620, 2924, 5020, 5564, 6232, 6368, … (последовательность A063990 в OEIS)

Внешние ссылки

См. также

be-x-old:Прыхільныя лікі br:Niver karantezus ca:Nombres amics da:Venskabstal gl:Números amigos he:מספרים ידידים hu:Barátságos számok is:Vingjarnlegar tölur la:Numeri amicabiles lmo:Nümar amiis lt:Draugiškasis skaičius nl:Bevriende getallen no:Vennskapstall pl:Liczby zaprzyjaźnione sl:Prijateljsko število sv:Vänskapliga tal th:จำนวนเชิงมิตร

Источник

Дружественные числа

Всего получено оценок: 141.

Всего получено оценок: 141.

Математика полна интересных загадок и не всегда понятных закономерностей. Математики древности считали, что можно всю вселенную изучить с помощью чисел, нужно только найти правильные закономерности, как показывает история – они оказались правы. Одной из интересных математических закономерностей являются дружественные числа, о которых и пойдет речь сегодня.

Что такое дружественное число?

Вспомним, что любое число имеет делители, то есть числа, на которые число поделиться нацело. Если у одного числа сумма всех делителей равна второму числу, а у второго числа сумма всех делителей равна первому, то такие числа называются дружественными.

Название закономерности пошло от Пифагора. Когда у древнего математика спросили, кто есть друг, он ответил, что для него друг – человек, повторяющий его самого. В качестве примера Пифагор привел два числа 220 и 284. А нашедшие закономерность ученики назвали числа дружественными друг другу.

Пример дружественных чисел

Рассмотрим наиболее простой пример дружественных чисел, приведенный еще Пифагором.

Делители числа 220: 1;2;4;5;10;11;20;22;44;55;110

Делители числа 284: 1;2;4;71;142

Если просуммируем все делители первого числа, то получится 1+2+4+5+10+11+20+22+44+55+110=284.

А теперь просуммируем делители числа 284: 1+2+4+71+142 = 220 – так и выглядит в математике эффект дружественных чисел.

Обратите внимание на то, что само число не считается делителем. Но при этом любое число можно поделить на само себя и получить в результате 1. А вот 1 считается делителем любого числа.

Сколько всего дружественных чисел?

Открывателем первой пары дружественных чисел был Пифагор. Эта пара наименьшая, ближе к началу числовой прямой таких чисел нет. После Пифагора ни один математик не мог открыть следующую пару чисел целых 15 веков, то есть полтора тысячелетия.

Третью пару нашел Ране Декарт в 1638 году, а через 100 лет Эйлер излагает 5 различных методов выявления дружественных чисел и преподносит их 59 пар!

С изобретением метода выявления дружественных чисел, пары стали находить все чаще и чаще. На 2019 год найдено больше 1 миллиарда дружественных чисел и пары продолжают находить. Интересно, что до сих пор математики не выяснили, является ли число дружественных пар конечным, или их бесконечно много.

Что мы узнали?

Мы поговорили о дружественных числах. Узнали, что это такое и поговорили об истории открытия математической зависимости. Сказали, сколько дружественных чисел открыто на данный момент.

Источник

Дружественные номера

оглавление

Примеры

Свойства и нерешенные проблемы

Ранние упоминания и приговор Сабиту ибн Курре

Пифагор впервые упоминается около 500 г. до н.э. Дружественные числа 220 и 284. Когда его спросили, что за друг, он ответил: «Тот, кто отличается от меня, например 220 и 284».

И аль-Фариси, и Ибн аль-Банна использовали фразу из Сабита ибн Курры :

Примеры

Предложение Леонарда Эйлера

Леонард Эйлер обобщил теорему Табита:

В 1946 году Эскотт опубликовал полный список из 390 дружественных пар чисел, которые были известны до 1943 года.

В 2007 году было известно, что дружными являются почти 12 миллионов пар чисел.

В мае 2018 года было известно 1 222 206 716 пар чисел.

Считается, что существует бесконечное количество дружественных чисел, но никаких доказательств пока нет.

Теорема Вальтера Борхо

Более удобные числа можно найти с помощью теоремы Уолтера Борхо :

С помощью этой теоремы Борхо нашел еще 10 455 дружественных чисел.

Обычные пары дружественных чисел

Первые числа из самых маленьких обычных дружественных пар чисел:

Если дружественная пара чисел не является правильной, то это неправильная дружественная пара чисел (или экзотическая, дружественная пара чисел ).

Пара близнецов, которые дружат

Первые пары близнецов, которые подружились, следующие:

обобщение

Связанные классы чисел

Квази-дружественные числа

Первые квази-дружественные пары чисел:

Общительные числа

Представляет собой цепочку (конечную последовательность) более двух целых чисел перед, каждое из которых сумма собственных делителей предшествующего числа и первого числа является суммой собственных делителей последнего числа, она называется (англ. Of social цифры общительные числа ). В настоящее время (по состоянию на ноябрь 2017 г.) известны цепочки порядка (длины) 4, 5, 6, 8, 9 и 28.

В ноябре 2017 года было известно 5410 таких сетей.

Под аликвотными последовательностями (цепочками содержимого) подразумеваются те последовательности, в которых сумма собственного делителя последующего элемента равна последующему члену. Таким образом, общительные числа образуют периодические аликвотные последовательности.

Источник