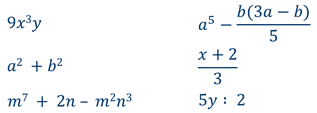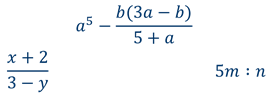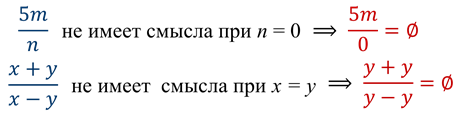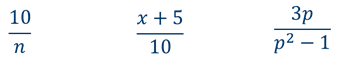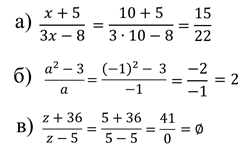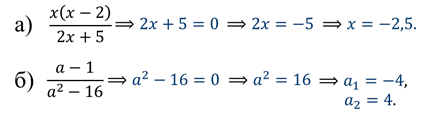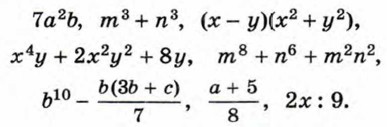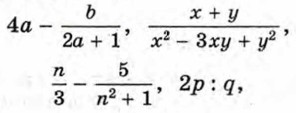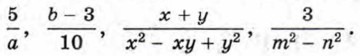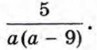Что такое дробные выражения 8 класс алгебра

Рациональные выражения

Урок 1. Алгебра 8 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Рациональные выражения»

На этом уроке мы вспомним, какие выражения называют целыми и дробными. Познакомимся с рациональными выражениями. Узнаем, какие значения называют допустимыми. А также научимся находить допустимые значения выражения.

Вы уже знакомы с целыми и дробными выражениями. Давайте вспомним их определения.

Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.

В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.

Целые и дробные выражения называют рациональными выражениями.

Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.

Напомним, что целые выражения имеют смысл при любых значениях переменных. Чтобы найти значение целого выражения, нужно подставить указанное значение переменной и выполнить все действия.

Дробное выражение при некоторых значениях переменных может не иметь смысла.

Чтобы найти значение рационального выражения, надо:

1) подставить числовое значение переменной в данное выражение;

2) выполнить все действия.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

Множество всех допустимых значений переменных называется областью допустимых значений (коротко ОДЗ) или областью определения выражения.

Как вы уже знаете, выражение вида называется дробью.

Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.

Найдите значение дроби.

Найдите допустимые значения переменной в выражениях:

Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.

В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.

Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.

Чтобы найти значение рационального выражения, надо:

1) Подставить числовое значение переменной в данное выражение;

2) Выполнить все действия.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

Множество всех допустимых значений переменных называется областью допустимых значений или областью определения выражения.

Источник

Алгебра. 8 класс

Целые выражения – это такие выражения, которые состоят из чисел и переменных с помощью действий сложения, вычитания, умножения и деления на число, отличное от нуля.

Дробные выражения – это выражения, которые помимо действий сложения, вычитания, умножения и деления на число, отличное от нуля, содержат деление на выражение с переменными.

Целые и дробные выражения вместе называют рациональными выражениями.

Дробь – это выражение вида .

Целое выражение имеет смысл при любых значениях входящих в него переменных, потому что действия для нахождения значения целого выражения, всегда возможны.

Дробное выражение при некоторых значениях переменной может не иметь смысла.

• не имеет смысла при x = 0.
• не имеет смысла при x = y.

Дробные выражения имеют смысл при любых значениях входящих в них переменных, кроме тех, что обращают знаменатель в нуль.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями.

Рациональная дробь – это дробь, числитель и знаменатель которой многочлены.

Примеры

В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.

Чтобы найти допустимые значения переменных в дроби, необходимо:

• Приравнять знаменатель, содержащий переменные, к нулю.
• Решить полученное уравнение. Корни этого уравнения будут являться теми значениями переменных, которые обращают знаменатель в нуль.
• Исключить эти значения из всех действительных чисел.

Пример 1.
Найти допустимые значения переменной в дроби .

1) x(x + 1) = 0
2) x = 0 или x + 1 = 0
x = 0 или x = –1.
Корни уравнения 0 и – 1.
3) Допустимыми значениями x являются все числа, кроме 0 и –1.

Пример 2.
Найти значения x, при которых дробь равна нулю.

, когда x 2 – 1 = 0 и x + 1 ≠ 0.
1) x 2 – 1 = 0
2) (x – 1)(x + 1) = 0
x = ±1
3) x + 1 ≠ 0
x ≠ –1.
при x = 1.

Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.

Источник

Что такое дробные выражения 8 класс алгебра

В курсе алгебры 7 класса мы занимались преобразованиями целых выражений, т. е. выражений, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения

В отличие от них выражения

помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.

Целые и дробные выражения называют рациональными выражениями.

Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.

Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение не имеет смысла

при а = 0. При всех остальных значениях а это выражение имеет

смысл. Выражение имеет смысл при тех значениях х и у, x ≠ y.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

Выражение вида называется, как известно, дробью.

Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.

Примерами рациональных дробей служат дроби

В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.

Пример 1. Найдем допустимые значения переменной в дроби

Это уравнение имеет два корня: 0 и 9. Следовательно, допустимыми значениями переменной а являются все числа, кроме 0 и 9.

Дробь равна нулю тогда и только тогда, когда a = 0 и b ≠ 0.

2. Основное свойство дроби. Сокращение дробей

Мы знаем, что для обыкновенных дробей выполняется следующее свойство: если числитель и знаменатель дроби умножить на одно и то же натуральное число, то значение дроби не изменится. Иначе говоря, при любых натуральных значениях а, b и с верно paвенство

Докажем, что это равенство верно не только при натуральных, но и при любых других значениях а, b и с, при которых знаменатель отличен от нуля, т. е. при b ≠ О и с ≠ О.

Пусть Тогда по определению частного а = bm. Умножим обе части этого равенства на с :

На основании сочетательного и переместительного свойств умножения имеем:

Так как bс ≠ 0, то по определению частного

Мы показали, что для любых числовых значений переменных b и с, где b ≠ О и с ≠ 0, верно равенство

Равенство (1) сохраняет силу и в том случае, когда под буквами а, b и с понимают многочлены, причем b и с — ненулевые многочлены, т. е. многочлены, не равные тождественно нулю.

Равенство (1) выражает основное свойство рациональной дроби:

если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Это равенство верно при всех допустимых значениях переменных. Такие равенства будем называть тождествами. Ранее тождествами мы называли равенства, верные при всех значениях переменных. Теперь мы расширяем понятие тождества.

Определение. Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Основное свойство рациональной дроби позволяет выполнять приведение дроби к новому знаменателю и сокращение дробей. Приведем примеры.

Пример 1. Приведем дробь к знаменателю

Множитель называют дополнительным множителем к числителю и знаменателю дроби

Пример 2. Приведем дробь к знаменателю

Для этого числитель и знаменатель данной дроби умножим на -1:

если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному.

Пример 3. Сократим дробь

Разложим числитель и знаменатель дроби на множители:

Сократим полученную дробь на общий множитель a + 3:

Пример 4. Построим график функции

Графиком функции является прямая, а графиком функции но с «выколотой» точкой (4 ; 4) (рис. 1.)

Источник

Рациональные выражения

В курсе алгебры 7 класса мы занимались преобразованиями целых выражений, т. е. выражений, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения

В отличие от них выражения

помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.

Целые и дробные выражения называют рациональными выражениями.

Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.

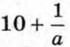
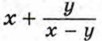
Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение не имеет смысла при а = 0. При всех остальных значениях а это выражение имеет смысл. Выражение имеет смысл при тех значениях х и у, когда х ≠ у.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

Выражение вида 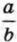называется, как известно, дробью.

Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.

Примерами рациональных дробей служат дроби

В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.

ИСААК НЬЮТОН (1643—1727) — английский физик, механик, математик и астроном. Сформулировал основные законы классической механики, открыл закон всемирного тяготения, разработал, независимо от Лейбница, основы математического анализа.

Пример 1. Найдём допустимые значения переменной в дроби

Это уравнение имеет два корня: 0 и 9. Следовательно, допустимыми значениями переменной а являются все числа, кроме 0 и 9.

Пример 2. При каком значении х значение дроби 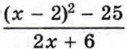равно нулю?

Источник

Урок по алгебре в 8 классе на тему: «Дроби. Дробные выражения. Рациональные выражения. Допустимые значения переменных».

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

МБОУ «Нововикринская СОШ».

Автор учитель математики Казумбекова Кистаман Магомедовна.

Урок по алгебре в 8 классе на тему: «Дроби. Дробные выражения. Рациональные выражения. Допустимые значения переменных».

Цель: добиться усвоения учащимися содержания понятий: целое выражение, дробное выражение, рациональное выражение, рациональное дробь, допустимые значения переменной в выражении; сформировать у учащихся умения выделять названные виды выражений среди предложенных выражений с переменными, а также выполнять действия, которые имеют целью нахождение ОДЗ дробного выражения.

Тип урока: усвоение знаний, умений и навыков.

Наглядность и оборудование: опорный конспект «Дробные выражения. Рациональные выражения».

I. Организационный этап

Вступительное слово учителя

· Особенности изучения алгебры в 8 классе;

· организация учебного процесса;

Учитель проверяет летнее домашнее задание (если такое было задано).

С целью осознания учащимися необходимости изучения вопроса о видах рациональных выражений предлагаем учащимся задание:

Какой из выражений: х2, х + 2ху, , лишний? Почему?

После обсуждения с учащимися результатов выполнения предложенного задания формируется мнение: в 7 классе был изучен вопрос о виды, свойства и способы преобразования выражений, не содержит деления на переменную (целые выражения); в 8 классе пришло время изучить виды, свойства и способы преобразований выражений, содержащих деление на переменную(дробные выражения), а также обобщить знания учащихся о видах выражений и логическую связь между ними. Этот вывод и является основной дидактической целью изучения раздела.

@ целях успешного восприятия учащимися учебного материала урока перед изучением новой темы следует активизировать знания учащихся о алгоритмы выполнения действий с рациональными числами, способы преобразования целых рациональных выражений и способы решения линейных уравнений и уравнений, сводящихся к линейным (изученные в 7 классе).

Выполнение устных упражнений

1. Найдите значения выражений:

2. Вычислите:
; ; ; ; ; ; 19 · 0,1; 7 : 0,1; ; .

5. Представьте выражения в виде произведения:

6. Преобразуйте выражения в многочлен стандартного вида:

План изучения нового материала

2. Дробные выражения.

3. Рациональные выражения.

4. Рациональный дробь.

5. Допустимые значения переменных в выражении (ОДЗ).

Дробные выражения. Рациональные выражения

1. Целые выражения состоят из чисел, букв и степеней и действий сложения, вычитания, умножения, возведения в степень и деления, кроме деления на переменную.

!Любое целое выражение можно представить в виде многочлена.

2. Дробные выражения обязательно содержащие действие деления на выражение с переменной (переменными), а также могут содержать все действия, которые есть в целом выражении.

3. Целые выражения вместе с дробными выражениями называют рациональными выражениями.

Пример. ; ; — рациональные дроби.

!Для рационального дроби допустимые значения переменной определяются из условия В ≠ 0 (знаменатель не должен равняться 0).

Итак, ОДЗ переменной а в выражении можно записать так:

6. Рациональный дробь равна 0, тогда и только тогда, когда А = 0 и В ≠ 0 (или )

Чтобы найти значение переменной, при котором рациональный дробь равна 0, надо:

а) найти ОДЗ дроби (из условия В ≠ 0);

б) приравнять числитель к нулю (А = 0) и найти соответствующие значения переменных;

в) из значений, полученных в п. б) исключить те, что не входящие в ОДЗ (см. п. а.).

Пример. При каком значении переменной дробь равна нулю?

@ Изучения материала урока начинается с повторения видов целых выражений, которые изучали ученики в 7 классе (одночлен, многочлены), и обобщение представлений учащихся об их структуру и свойства (все целые выражения содержат 5 арифметических действий, кроме деления на выражение с переменными, и могут быть представлены в виде многочлена).

Далее формируется представление учащихся о содержании понятия рационального дроби как особого случая дробного выражения и о содержании понятия допустимого значения переменной в выражении и области допустимых значений переменной (ОДЗ) в выражении (при этом можно опираться на приобретенные учащимися в 7 классе знания о содержании понятия области определения функции).

Выполнение устных упражнений

1. Какие из выражений являются целыми; дробными? Какие из выражений являются дробями; рациональными дробями?

а) ; б) ; в) ; г) ; д) ; е) .

3. При каких значениях переменной выражение не имеет смысла? Назовите допустимые значения переменной в выражении:

а) ; б) ; в) ; г) .

4. Какие из приведенных равенств является тождественностями?
а) ; б) ; в) .

Выполнение письменных упражнений

@ Для реализации дидактической цели на этом уроке следует решить задачи следующего содержания:

1. Среди представленных выражений с переменными выбрать: целые, дробные выражения, рациональные дроби.

1) Какие из выражений являются целыми; дробными? Какие из выражений являются дробями; рациональными дробями?

а) ; б) ; в) ; г) ; д) ; е) .

а) целыми выражениями; б) дробными выражениями.

2. Нахождение значения дробного выражения при данных значениях переменных.

1) Найдите значение выражения:

г) при b = 3;

д) при x = ;

есть) при в = 1,5.

2) Чему равно значение дроби при:

3. Нахождение допустимых значений переменных в выражении.

1) Укажите допустимые значения переменной в выражении:

а) ; б) ; в) ; г) .

2) Найдите допустимые значения переменной в выражении:

а) ; б) ; в) .

4. Составление выражений с переменными по условию задачи.

Автомобиль проехал 195 км за? ч. Запишите в виде выражения скорость автомобиля. Найдите значение этого выражения при t = 3. Выполнение упражнений на повторение: арифметические действия с обыкновенными дробями (сокращение, сравнение, сложение, вычитание, разложение целых выражений на множители с применением различных способов.

1) Преобразуйте в многочлен:

2) Разложите многочлен на множители:

3) Разложите на множители:

1) Какие выражения называют целыми? Приведите примеры.

2) Какие выражения называют дробными? Приведите примеры.

1. Изучить определения понятий, рассмотренных на уроке.

2. Решить упражнения на: классификацию рациональных выражений, нахождение ОДЗ выражений, вычисление значений выражений с переменными, числовых выражений, содержащих обыкновенные дроби, решение целых уравнений.

Источник