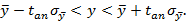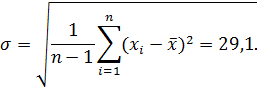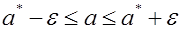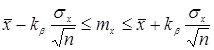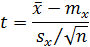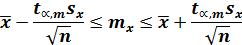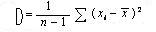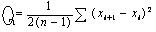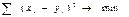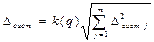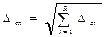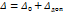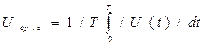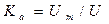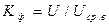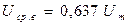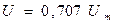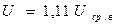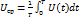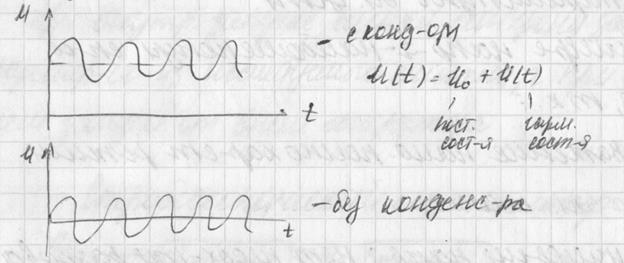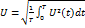Что такое доверительная вероятность измерений
Доверительная вероятность и доверительный интервал.
Вероятность того, что истинное значение измеряемой величины лежит внутри некоторого интервала, называется доверительной вероятностью, или коэффициентом надежности,а сам интервал — доверительным интервалом.
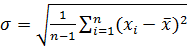
на так называемый коэффициент Стьюдента. Коэффициенты Стьюдента 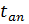
| Число измерений n | Доверительная вероятность y | ||
| 0,67 | 0,90 | 0,95 | 0,99 |
| 2,0 | 6,3 | 12,7 | 63,7 |
| 1,3 | 2,4 | 3,2 | 5,8 |
| 1,2 | 2,1 | 2,8 | 4,6 |
| 1,2 | 2,0 | 2,6 | 4,0 |
| 1,1 | 1,8 | 2,3 | 3,3 |
| 1,0 | 1,7 | 2,0 | 2,6 |
Окончательно, для измеряемой величины y при заданной доверительной вероятности y и числе измерений n получается условие
Величину 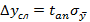
Пример: см. лекцию №5 – ряд чисел.
При числе измерений – 45 и доверительной вероятности – 0,95 получим, что коэффициент Стьюдента приблизительно равен 2,15. Тогда доверительный интервал для данного ряда измерений равен 62,6.
Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором:
— неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;
— неправильная запись результата наблюдений, значений отдельных мер использованного набора, например, гирь;
— хаотические изменения параметров напряжения, питающего средства измерения, например, его амплитуды или частоты.
Доверительный интервал и доверительная вероятность



Для подавляющего большинства простых измерений достаточно хорошо выполняется так называемый нормальный закон случайных погрешностей (закон Гаусса), выведенный из следующих эмпирических положений.
1) погрешности измерений могут принимать непрерывный ряд значений;
2) при большом числе измерений погрешности одинаковой величины, но разного знака встречаются одинаково часто,
3) чем больше величина случайной погрешности, тем меньше вероятность ее появления.

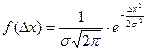
где 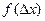


Величина σ не является случайной величиной и характеризует процесс измерений. Если условия измерений не изменяются, то σ остается постоянной величиной. Квадрат этой величины называют дисперсией измерений. Чем меньше дисперсия, тем меньше разброс отдельных значений и тем выше точность измерений.
Точное значение средней квадратичной ошибки σ, как и истинное значение измеряемой величины, неизвестно. Существует так называемая статистическая оценка этого параметра, в соответствии с которой средняя квадратичная ошибка равняется средней квадратичной ошибке среднего арифметического 
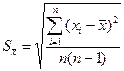
где 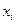
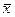
Чем больше число измерений, тем меньше 
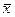

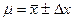
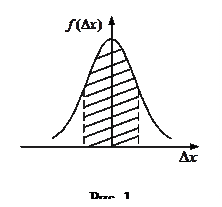
Интервал значений от 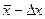
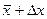

Все это справедливо для достаточно большого числа измерений, когда 
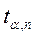


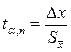
Функция распределения табулирована (табл.1). Значение коэффициента Стьюдента находится на пересечении строки, соответствующей числу измерений n, и столбца, соответствующего доверительной вероятности α
Таблица 1.
| n | α | n | α | ||||
| 0,8 | 0,9 | 0,95 | 0,98 | 0,8 | 0,9 | 0,95 | 0,98 |
| 1,9 | 2,9 | 4,3 | 7,0 | 1,5 | 2,0 | 2,6 | 3,4 |
| 1,6 | 2,4 | 3,2 | 4,5 | 1,4 | 1,9 | 2,4 | 3,1 |
| 1,5 | 2,1 | 2,8 | 3,7 | 1,4 | 1,9 | 2,4 | 3,9 |
Пользуясь данными таблицы, можно:
1) определить доверительный интервал, задаваясь определенной вероятностью;
2) выбрать доверительный интервал и определить доверительную вероятность.
При косвенных измерениях среднюю квадратичную ошибку среднего арифметического значения функции 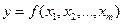
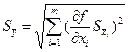
Доверительный интервал и доверительная вероятность определяются так же, как и в случае прямых измерений.
Доверительные интервалы и доверительная вероятность
Точечные оценки имеют тот недостаток, что по ним нельзя судить о точности полученных оценок. Поэтому возникает задача определения на основании выборочных значений такого интервала, который покрывал бы неизвестной значение параметра с заданной вероятностью.
В отличие от точечной оценки, интервальная оценка позволяет получить вероятностную характеристику точности оцениваемого параметра.
Выборочные параметры являются случайными величинами, их отклонения от генеральных (т.е. погрешности их определения) также будут случайными. Оценка этих отклонений носит вероятностный характер – можно лишь указать вероятность той или иной погрешности. Для этого в математической статистике пользуются доверительными интервалами и доверительными вероятностями.
Доверительный интервал – интервал, который с заданной вероятностью накроет неизвестное значение оцениваемого параметра распределения.
Доверительная вероятность – вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным.
Оценивание с помощью доверительного интервала – способ оценки, при котором с заданной доверительной вероятностью устанавливают границы доверительного интервала.
Пусть для генерального параметра a получена из опыта несмещенная оценка a*. Нужно оценить возможную при этом ошибку. Назначим достаточно большую вероятность β – такую, что событие с этой вероятностью можно считать практически достоверным, и найдем такое значение ε для которого

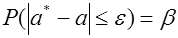
называемой уровнем значимости или риском. Уровень значимости часто выражают в процентах. Иначе формулу ( (5.8.1* ) можно интерпретировать как вероятность того, что истинное значение параметра а лежит в пределах
Вероятность β называется доверительной вероятностью, доверительным уровнем или надежностью, т.к. она характеризует надежность полученной оценки.
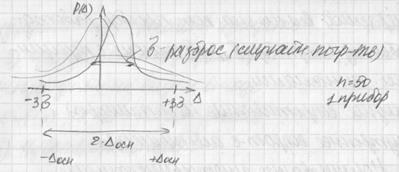
Интервал 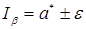
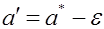
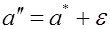
При этом отметим следующее. Ранее мы рассматривали вероятность попадания случайной величины на заданный (неслучайный) интервал. В данном случае дело обстоит иначе: величина ане случайна, зато случаен интервал I b . Случайно его положение на числовой прямой, определяемое его центром а * , случайна и длина интервала 2 e, так как величина e вычисляется, как правило, по опытным данным, т.е. по результатам эксперимента. Поэтому в рассматриваемом случае удобно толковать интервал I как вероятность того, что случайный интервал I b накроет величину а.
Величина доверительного интервала зависит от доверительной вероятности, с которой гарантируется нахождение параметра внутри доверительного интервала: чем больше величина β, тем больше и ε (т.е. с чем большей вероятностью мы хотим гарантировать полученный результат, тем в большем интервале он должен находиться).
Увеличение числа опытов проявляется в сокращении доверительного интервала при постоянной доверительной вероятности или в повышении доверительной вероятности при сохранении доверительного интервала.
ППри построении доверительного интервала решается задача об абсолютном отклонении:
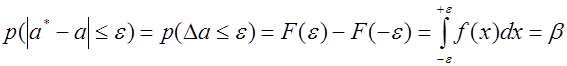
Таким образом, если известен закон распределения оценки a*, то задача определения доверительного интервала решается довольно просто.
Рассмотрим построение доверительного интервала для математического ожидания нормально распределенной случайной величины с известным генеральным стандартом σх.
Понятие генерального стандарта тесно связано с понятием точности прибора. Класс точности прибора – это выраженная в процентах относительная предельная погрешность измерения величины, равной пределу измерения прибора. В измерительной технике в большинстве отраслей промышленности под предельной погрешностью понимается величина, равная двум среднеквадратическим отклонениям
Пусть имеется выборка объема n значений случайной величины. Оценкой mx является среднее выборки:
Для построения доверительного интервала необходимо знать распределение этой оценки. Для выборок из генеральной совокупности, распределенной нормально можно показать, что 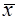
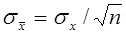
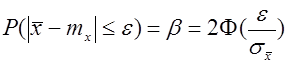
Задавшись доверительной вероятностью, определим по таблице значение функции Лапласа 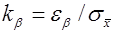
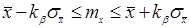
Из оценки видно, что уменьшение доверительного интервала обратно пропорционально квадратному корню из числа наблюдений. Следовательно, если надо уменьшить возможную ошибку в два раза надо увеличить число наблюдений в 4 раза.
Если закон распределения оценки не известен, то в математической статистике применяют обычно два метода:
1) приближенный – при n более 50 заменяют неизвестные параметры их оценками;
2) от случайной величины a * переходят к другой случайной величине, закон распределения которой не зависит от оцениваемого параметра а, а зависит только от объема выборки n и от вида распределения величины Х. Такого рода величины наиболее подробно изучены для нормального закона. В качестве доверительных границ берут симметричные квантили
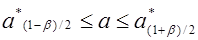
Если выразить через р,
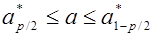
На практике, как правило, число измерений конечно и не превышает 10…30. При малом числе измерений фактическая дисперсия 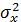
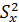
t – случайная величина, имеющая распределение, отличное от нормального, зависящее от числа степеней свободы(t – распределение или распределение Стьюдента). При больших значениях n распределение Стьюдента приближается к стандартному нормальному распределению. И, по аналогии, получаем построение доверительного интервала
Дата добавления: 2020-12-22 ; просмотров: 716 ; Мы поможем в написании вашей работы!
Доверительная вероятность. Доверительный интервал.
Δr – доверительный интервал
Интервал значений случайной величины внутри которого с заданной вероятностью находится истинное значение измеряемой величины, называется доверительны интервалом, а соответствующая ей вероятность – доверительной вероятностью (Pд)
В соответствии со стандартом, принимают 4 градации доверительной вероятности
| Рд | 0.9 | 0.95 | 0.975 | 0.99 |
| q | 0.1 | 0.05 | 0.025 | 0.01 |
q – уровень значимости результата.
0,9;0,1 – для оценочных расчетов
0,95;0,05 – для технически расчетов
0,975 – для точных технических расчетов
0,99 – для особо ответственных расчетов
19. Статистические методы исключения грубых промахов.
Методика применяется к многократным измерениям
Оценка грубых промахов реш. методом мат. статистики.
Суть метода: выдвигается нулевая гипотеза, что сомнительных результат принадлежит к совокупности измерений, а затем пользуясь статистическими критериями опровергают данную гипотезу, и результат отбрасывается.
Методы подбора критериев:
1) Критерий позволяет отбросить результат резко отличающийся от среднего арифметического

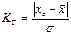
ZГ(n,q) = f(q,n)– теор. знач. критер. Греббса
q – уровень значимости
КГ>ZГ – результат отбрасывается
Формулу f(q,n) придумал Гребс для больших n, Шарле и Шавене для малых
2) Критерий позволяет отбросить результат резко отличающийся от соседних результатов


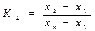
Если КΔ>ZΔ, то результат отбрасывается
20. Статистические методы исключения систематических погрешностей.
Есть случайные и систематические составляющие. Сначала надо определить есть ли систематическая составляющая
Критерий для оценки наличия систематической прогрессирующей погрешности (критерий Аббе)
Но это всё определяется не точно на 100%, а с некоторой доверительной вероятностью
Метод наименьших квадратов (исключение систематической составляющей)
Нужно, чтобы сумма квадратов разности была минимальной
21. Методика оценки погрешности при прямых измерениях с однократным наблюдением.
Для оценки точности при однократных измерениях надо иметь информацию об измерительном средстве, о методе измерения, об условиях измерения и об опыте оператора.
Расчёт погрешности на основе допустимых предельных погрешностей, без учёта разбиения погрешности на случайную и систематическую составляющие.
В основе методики – принцип наихудшего случая, т.е. что погрешность носит систематический характер и имеет один знак.
Методика даёт завышенный, но надёжный результат с вероятностью ≈ 1
Расчёт погрешности с учётом систематической и случайной составляющей
K – коэффициент, зависящий от уровня значимости результата и числа n.
n – число измерений
r – число интервалов
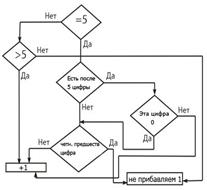
23. Правила округлений результатов измерений.
1) Погрешность результатов измерений указывается 2-мя значащими цифрами, если первая из них 1 или 2 и одной цифрой в остальных случаях.
2) Результат измерения округляют до того же десятичного знака, кот. оканчивается округленное значение абс. погрешности.
24. Средства измерений. Их классификация.
Средства измерений – техническое устройство предназначенное для измерений, имеющее нормированные метрологические характеристики воспроизвод. и хранящее ед. физ. вел, размер кот. принимается неизменным в теч. известного интервала времени.
1.по метролог. назначению
-метролог.(для работы метролог. служб)
2.по конструктивному исполнению
Мера – средство измерения, предназначенное для хранения и воспроизведения размера физ. вел.
Измерительный преобразователь – средство измерения, предназначенное для получения значения измеряемой величины в сигнал, удобный для передачи, хранения, обработки.
Он может быть отдельным прибором, тогда это датчик, но чаще он встроен в измерительный прибор
Измерительный прибор – средство измерения, предназначенное для измерения в заданном диапазоне, имеющее нормированные метролог. характеристики.
Измерительные системы – совокупность средств измерений и вычислительных средств, объединённых в единую систему.
3.по уровню автоматизации
ГОСТ дел. все приборы на 20 групп
М – измерит. мощности
У – измерит. усилители
Ц – комбинированные приборы
25. Основные метрологические характеристики электро-радиоизмерительных приборов.
Метрологическая хар-ка – это свойство средства измерения, влияющая на погрешность измерения.
1)Погрешность измеряемого средства
2)Диапазон показаний и измерений
Диапазон измерений – часть диапазона показаний, где обеспечивается нормированная точность.
3)Предел измерений – наим. и наиб. значение диапазона измерений
4)Градуированная характеристика – зависимость измерения показаний от измеряемой величины.
5)Чувствительность измерит. прибора- отношение измеренного сигнала на выходе к вызывающему его входному сигналу.
6)Разрешающая способность – min изменение входного сигнала, кот. различимо по показанию прибора
7)Быстродействие – число измерений в ед. времени
8)Внутреннее сопротивление (для приборов подключённых последовательно)
9)Входное сопротивление прибора (для приборов подключённых ||)
Может быть активным и реактивным
10)Вариация показаний – разница, показаний при плавном подходе к измеряемой точке при изменении измеряемой вел (Гистерезис). Характерно для динамических измерений
11)Мощность потребляемая от измерительной цепи
Она должна стремиться к 0.
26. Нормирование инструментальной погрешности
Нормировать можно в формах:
Основная и дополнительная погрешности нормируются отдельно
Типовые метрологические характеристики:
Обычно нормирование производится первой партии выпускаемых приборов (испытание на точность)
Измерение производятся в нормальных условиях
Измерения повторить для точек диапазона и некоторых точек в диапазоне.
Дополнительная погрешность измеряется так же, как и основная, но измеряются условия измерения (по каждому параметру измеряется отдельно)
27. Классы точности средств измерений.
Класс точности прибора- это основная метрологическая характеристика.
Класс точности количественно выражается в форме предела допустимой абс., относит. или приведенной погрешности.
Для радиоизмерит. приборов класс точности выражается пределом относит. или приведенной погрешности. Формулу для расчета погрешности приводят в паспорте на прибор. Используются одночленные формулы (погрешность имеет аддитивную составляющую) и двучленные (аддитивная составл. + мультипликативная)
28. Измерение напряжения и других параметров электрической цепи. Измеряемые значения переменного напряжения.
Напряжения и токи могут быть постоянными и переменными. При измерении постоянного напряжения прибор будет указывать на его действительное значение. При измерении переменного напряжения в зависимости от применяемого прибора для измерений может быть получена одна из следующих величин:
-амплитудное значение переменного напряжения,
-среднеквадратичное значение (действительное значение).
Мгновенное значение напряжения переменного тока является функцией времени и определяется следующей формулой:
Где:
ω- круговая частота,
Среднее значение напряжения определяется по формуле:
Для симметричного синусоидального переменного (гармонического) напряжения это значение будет равно нулю. Поэтому для оценки гармонического переменного напряжения эта характеристика не применяется. Она может быть применена для выделения постоянной составляющей негармонического переменного напряжения.
Средневыпрямленное значение напряжения определяется по формуле:
Выпрямление может быть однополупериодное и двухполупериодное. При однополупериодном выпрямлении в формулу ( 3 ) надо добавить коэффициент 0,5.
Среднеквадратичное значение напряжения определяется по формуле:
ния называют также действующим значением переменного напряжения или тока.
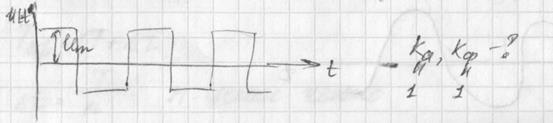
Амплитудное, средневыпрямленное и среднеквадратичное значения напряжения связаны между собой коэффициентами амплитуды и формы.
Для гармонического напряжения Ка = 1,41, а Кф =1,11. То есть различные значения напряжения для гармонического сигнала связаны соотношениями:
29. Приборы для измерения напряжения и других параметров электрической цепи.
Измерение напряжения – наиболее популярный способ измерения так как :
1) Напряжение наиболее полно характеризует режим работы электрической схемы
2) При измерении напряжения не необходимости разрыва электрической цепи
3) Измеряя напряжение, косвенным методом можно измерить другие параметры (I,R)
Токи и напряжение могут быть постоянными и переменными. Когда напряжение постоянное, то прибор показывает его действующее значение, когда переменное – прибор может измерять разные значения. В этом случае надо знать какой прибор как работает
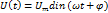
Характеристики переменного напряжения :
1) Амплитудное значение
2) Среднее значение
4) Действующее значение среднеквадратичное
Для гармонического сигнала Uср в = 0,637 Um
Для оценки формы сигнала:
Коэффициент амплитуды : Ка = Um / U =1,41
Коэффициент формы : Кф = U/ Uср в = 1,11
Классификация приборов для измерения напряжения
По виду измеряемого параметра приборы могут быть:
-измерители ёмкости, индуктивности
Если прибор измеряет несколько параметров он называется мультиметром
Все измеряющие приборы
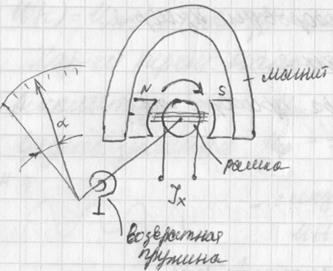
Электромагнитные приборы относятся к приборам непосредственной оценки. Обычно в таких приборах электрическая энергия преобразуется в механическую энергии. (?в част.? Во вращательное движение стрелочного механизма)
Они строятся по следующим измерительным схемам: машинно-электрическая, электромагнитная, электростатичесая, электродинамическая, магнитноэлектрическая
Высокая точность, высокая чувствительность (класс 0,1; 0,5)
Все остальные измеряемые системы более грубые
Используется для точных механических приборов
Недостатки: Большое потребление энергии от источника
Электростатические системы используются для высокочастотных измерений (используется конденсатор)
Электродинамические системы потребляют много энергии, для измерителей мощности, счётчиков электрической энергии
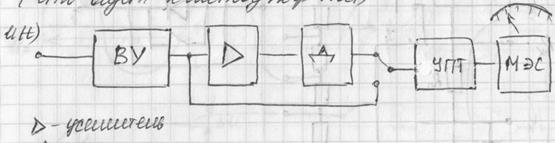
Электронноаналоговые приборы – используются те же принципы как и в электромеханических
Основной недостаток электрических систем – большое ….
Потребление мощности от измеряемой цепи, что ведет к методической погрешности
Треугольник-усилитель переменного напряжения
УПТ-усилитель постоянного тока
Достоинство: за счет усилителей данный прибор не отнимает энергию от измеряемой цепи. Имеет высокую чувствительность и точность. В основном используется для измерения малых величин.
Цифровые приборы:
ЦОУ-цифровое отсчетное устройство
30. Осциллографы. Назначение и классификация осциллографов.
Для измерения параметров динамических сигналов используют специальные приборы. Для детерминированных сигналов используют осциллографы, для случайных сигналов –измерители параметров случайных сигналов. (Измерение математического ожидания, дисперсии, среднего квадратичного отклонения, корреляционных характеристик и др.).
Электронный осциллограф предназначен для визуального отображения формы и приближенного измерения параметров периодических сигналов сложной формы.
Наряду с тестерами, цифровыми вольтметрами и импульсными генераторами осциллографы являются наиболее распространенными измерительными приборами и очень широко применяются на всех стадиях проектирования, производства и обслуживания ЭВМ.
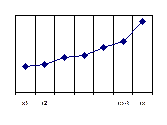
Осциллограф позволяет получить на экране электронно-лучевой трубки график одного или нескольких периодов входного сигнала в координатах «время – напряжение», т.е. график функции y=f(t). Пример такого графика показан на рис.
1. Универсальные О. 100МГц
2. Стробоскопические О. – Они используются для измерения высокочастотных сигналов, либо кратковременных повторений сигналов до 10МГц работ.
3. Запоминающие О. для исследования однократных, редко повторяющихся процессов.
4. Специальные О. – О. Целевого назначения, снятие видеосигнала; для переходных процессов.
2) многоканальные (2,4…)
Осциллографы делятся по исполнению:
1) аналоговые на ЭЛТ
2) цифровые с использованием матричных экранов
3) виртуальные приборы
31. Назначение и классификация измерительных генераторов.
Измерительные генераторы подразделяются на несколько групп (см. рис. 2.1).
Наиболее распространенными являются генераторы звуковой частоты ГЗ, высокой частоты Г4, прямоугольных импульсов Г5, качающейся частоты Г2.
Источник сигналов разнообразных форм и частот, предназначенные для регулирования, настройки и измерений в электронных схемах.
Они должны обладать:
1) возможностью регулировки выходных параметров
2) высокую стабильность
3) стандартные средства связи с др. измерительными устройствами
В зависимости от формы сигнала, генераторы делятся:
— генератор сигналов произвольной формы
— генератор случайных сигналов
— генератор стандартной частоты
По принципу пострения:
Практические рекомендации по работе с измерительными генераторами сводятся к следующему:
а) перед подключением генератора к нагрузке следует убедиться, что её сопротивление не меньше, чем минимально-допустимое по «Техническое описанию»,
б) соединять выход генератора с нагрузкой следует только входящими в комплект коаксиальными радиочастотными кабелями,
в) генераторы импульсов обеспечивают гарантированную по «Техническому описанию» форму только при работе на согласованную нагрузку.
г) прежде чем устанавливать длительность импульса и его задержку, необходимо приближенно вычислить длительность периода».
32. Измерение частоты и интервалов времени.
ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования.
Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем.
Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор.
ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: