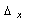Что такое доверительная погрешность

Научная электронная библиотека

Сибагатуллина А. М., Мазуркин П. М.,

2.6. Обработка результатов измерений

Обработка прямых измерений. Для характеристики большинства приборов часто используют понятие приведенной погрешности, равной абсолютной погрешности в процентах диапазона шкалы измерений. По приведенной погрешности приборы разделяются на классы точности. Класс точности указан на панели прибора.

Наибольшая инструментальная погрешность измеряется по формуле:

, (2.1)

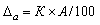
где К – класс точности, А – наибольшее значение шкалы прибора.

Инструментальную погрешность невозможно уменьшить статистической обработкой отсчетов.

При наличии случайных погрешностей наблюдаемые значения измеряемой величины при многократных измерениях случайным образом рассеяны относительно ее истинного значения. В этом случае действительное значение находят как наиболее вероятное из серии отсчетов, а погрешность характеризуют шириной интервала, который с заданной вероятностью показывает истинное значение [44].

Наилучшей оценкой истинного значения величины Х является выборочное среднее значение

, (2.2)

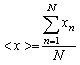
где 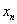– отсчет величины Х, – число отсчетов.

Для оценки разброса отсчетов при измерении используется выборочное среднее квадратическое отклонение отсчетов

. (2.3)

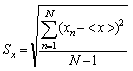
Выборочное среднее является случайной величиной и его разброс относительно истинного значения измеряемой величины оценивается выборочным средним квадратическим отклонением среднего значения

. (2.4)

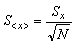
Доверительным интервалом называется интервал 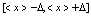, который с заданной степенью достоверности включает в себя истинное значение измеряемой величины.

Доверительной вероятностью (надежностью) результата серии наблюдений называется вероятность 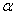, с которой доверительный интервал включает истинное значение измеряемой величины.

Случайную составляющую погрешности принято выражать как полуширину доверительного интервала. Случайная составляющая погрешности многократных измерений

, (2.5)

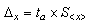
где 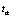– безразмерный коэффициент доверия (коэффициент Стьюдента).

Чем больше доверительная вероятность, тем надежнее оценка интервала и, вместе с тем, шире его границы.

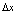
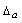
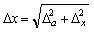
Полная абсолютная погрешность прямых измерений равна квадратической сумме ее составляющих: инструментальной – и случайной –

. (2.6)

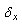
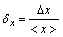
Полная относительная погрешность прямых измерений равна отношению полной абсолютной погрешности к выборочному среднему значению

. (2.7)

Обработка косвенных измерений [44]. Расчет погрешностей косвенных измерений осуществляется по алгоритму, использующему сложение абсолютных величин погрешностей.

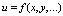
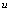
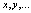
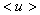
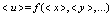
Пусть – функциональная зависимость между измеряемой величиной и величинами , значения которых найдены прямыми измерениями. Действительное значение определяется как:

. (2.8)

Вычисляем относительные погрешности аргументов. Затем определяем абсолютную и относительную погрешности функции

(2.9)

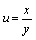
— для относительной погрешности

; (2.10)

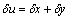
— для абсолютной погрешности

. (2.11)

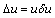
Оценка токсического действия тестируемой пробы воды. Оценка токсического действия тестируемой пробы воды делается на основании достоверности различий между показателями прироста численности клеток водорослей в контроле и в опыте. При этом вычисляют [14]:

– средние арифметические величины прироста численности клеток – X_i и X (в контроле и опыте);

– среднее квадратичное отклонение по формуле 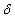(2.3);

– ошибку среднего арифметического (X):

– Td – критерий достоверности различий двух величин:

; (2.12)

, (2.13)

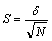
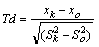
где x_k и x_о – сравниваемые средние величины (в контроле и опыте),

Sk 2 и So 2 – квадраты ошибок средних в контроле и опыте.

Td рассчитывают для каждой тестируемой пробы и сравнивают с табличной величиной Tst – стандартным значением критерия Стьюдента. В нашем случае для его определения принимаем уровень значимости р = 0,05 (95%) и степень свободы = (n1 + n2 – 2), т. е. (3 + 3 – 2) = 4. Tst при степени свободы 4 равно 2,78.

Если Td ≥ Tst, то различие между контролем и опытом достоверно – тестируемая вода загрязнена.

Источник

Большая Энциклопедия Нефти и Газа

Доверительная погрешность

Тем не менее очень часто доверительные погрешности рассчитывают, вводя ничем не обоснованное предположение о том, что вид закона распределения погрешностей будто бы точно известен. [3]

Тем не менее очень часто доверительные погрешности рассчитывают, вводя ничем не обоснованное предположение о том, что вид закона распределения погрешностей будто бы точно известен. [5]

Задаваясь определенными значениями доверительной вероятности, находят доверительную погрешность результата измерений и доверительный интервал для среднего квадратического отклонения. [6]

Увеличивать число наблюдений целесообразно до тех пор, пока доверительная погрешность измерения не будет определяться только систематической погрешностью. [7]

Когда число уравнений в системе равно количеству искомых параметров, последние, а также доверительные погрешности измерения этих параметров, находят методами косвенных измерений. С увеличением размерности условных уравнений, когда они линейны или линеаризованы, а результаты измерений равноточны и некоррелированы, используют МНК. Если погрешности измерений представляют нестационарный случайный процесс с известными характеристиками, например, известна функция ае ( I), то обработку данных и результатов измерений выполняют методом максимального правдоподобия. [9]

Если погрешности результатов измерений ограничиваются интервалами, верхняя и нижняя границы которых с заданной вероятностью включают погрешность результата измерений, то эти погрешности называются доверительными погрешностями. Доверительные погрешности характеризуются поставленными перед ними знаками или одним из этих знаков, если знаки распространяются только на одни положительные или отрицательные значения погрешностей. [14]

Qm) непрерывна вместе со своими производными первого и второго порядков в некоторой окрестности средних арифметических рядов измерений аргументов, и результаты прямых измерений аргументов распределены нормально, то по мере уменьшения их относительных средних квадратических отклонений закон распределения результата XQ косвенного измерения асимптотически приближается к нормальному. Поэтому для определения доверительной погрешности можно воспользоваться интегральной функцией нормированного нормального распределения, если число измерений велико. [15]

Источник

Категории статей

Двадцать второй год – взгляд из будущего

А ведь наше настоящее, для людей, живших сто лет назад, было будущим. Далее

Дыхание картошки

Овощи продолжают жизненный цикл даже после сбора урожая. Какие процессы идут в картошке? Далее

Грибы против пластика

Ученые проводят исследования по разложению пластика с помощью микроорганизмов и грибов. Далее

Ученые ставят диагноз планете

Cтолько углекислого газа, как сейчас, в атмосфере не было последние 2 млн лет, метана и закиси азота — 800 тыс. лет. Далее

Природный регулятор температуры колибри

Учитывая огромную скорость и частоту крыльев, птицы должны нагреваться до температур, несовместимых с жизнью. Далее

Популярные статьи

Польза и вред инфракрасного обогревателя (324011)

Среди электрических обогревателей, которые мы используем в быту, наиболее популярными сейчас становятся инфракрасные нагреватели. Они очень широко рекламируются в Интернете и в газетах. Говорят, что они намного эффективнее масляных радиаторов и тепловентиляторов. Меньше потребляют энергии, не сжигают кислород и т.д. Главное – они совершенно не вредные, никакого отрицательного воздействия на организм человека не оказывают. Далее

Почему горячая вода замерзает быстрее, чем холодная? (210365)

Это действительно так, хотя звучит невероятно, т.к в процессе замерзания предварительно нагретая вода должна пройти температуру холодной воды. Парадокс известен в мире, как «Эффект Мпембы». Далее

Вредно ли разогревать пищу в микроволновке? (199321)

Контролируйте температуру приготовления мяса! (181602)

При приготовлении сырого мяса, особенно, домашней птицы, рыбы и яиц необходимо помнить, что только нагревание до надлежащей температуры убивают вредные бактерии. Далее

451 градус по Фаренгейту, температура возгорания бумаги? (167620)

451 градус по Фаренгейту. Это название знаменитой книги Рэя Брэдбери. На языке оригинала звучит так: ‘Fahrenheit 451: The Temperature at which Book Paper Catches Fire, and Burns’. Действительно ли при этой температуре начинают гореть книги? Далее

Основные разделы

Вызывает ли доверие «доверительная» погрешность образцовых СИ?

Подобно основному вопросу философии «До какой степени познаваем мир?», метрология ставит вопрос «До какой степени измеряем мир?, т.е. на сколько точны наши оценки того или иного явления?». В приземленном, бытовом варианте это значит, что, используя какой-то измерительный прибор, мы хотим знать, до какой степени мы можем ему доверять.

Ближе к нашей термометрической тематике. Возьмем рабочий термометр сопротивления. Для рабочих термометров определен допуск, т.е. фактически допустимая погрешность Δ, равная отклонению показаний от стандартной зависимости НСХ. Поэтому критерий годности и разделение на классы не вызывает трудностей. Если термометр в допуске заявленного класса (с учетом неопределенности измерений), то он годен. Его можно подключать к вторичному прибору со стандартной НСХ и погрешность считываемых показаний будет в пределах допуска.

Сложнее обстоит дело с определением погрешности и сортировкой по разрядам образцовых термометров. Их градуировка индивидуальная. Номинальной характеристики для них нет. Чем же отличаются термометры например второго и третьего разряда? Согласно поверочной схеме – доверительной погрешностью.

Привожу выдержку из нового варианта текста поверочной схемы.

2.2.7 В качестве образцовых средств измерений 3-го разряда применяют меры температуры (аппаратуру для реализации реперных точек температурной шкалы, калибраторы температуры), платиновые термометры сопротивления, стеклянные, кварцевые, термоэлектрические термометры и другие, соответствующие по своим метрологическим характеристикам требованиям, предъявляемым к образцовым средствам измерений 3-го разряда.
2.2.8 Доверительные погрешности образцовых средств измерений 3 го разряда при доверительной вероятности 0,95 составляют от 0,02 до 17 °C при линейной зависимости от значения измеряемой величины. (красным здесь и далее выделена возможная опечатка, или ошибка, или вообще не понятная автору вещь)
2.2.9 Образцовые средства измерений 3-го разряда применяют для поверки рабочих средств измерений методом непосредственного сличения в термостате или методом прямых измерений в мерах температуры.

Дополним это информацией непосредственно из графической части схемы (часть 2)

Термометры (2разряд 0-1085 °С; δ = 0,01-0,1 °C) – (передача δ_м =0,003-0,4 °C) – (3 разряд 0-1085 °С; δ = 0,02-2,0 °C)

Меры температуры (2разряд 0-1085 °С; δ = 0,01-0,1 °C) – (передача δ_м =0,008-0,03 °C) – (3 разряд 0-1085 °С; δ = 0,05-0,5 °C)

Образцовые платинородий-платиновые термоэлектрические преобразователи (2разряд 300 ÷ 1200 °С; δ = 0,35-1 °C) – (передача δ_м =0,05-0,1 °C) – (3 разряд 0-1085 °С; δ = 0,35-1 °C )

Образцовые платинородиевые термоэлектрические преобразователи (2разряд 600 ÷ 1800 °С; δ = 0,8-4 °C) – (передача δ_м =0,05-0,1 °C) – (3 разряд 600-1800 °С; δ = 0,8-4 °C )

Итак, основной метрологической характеристикой образцовых СИ является доверительная погрешность. Что такое доверительная погрешность образцовых средств измерений при доверительной вероятности 0,95? Как она рассчитывается при поверке и может ли она быть достаточным критерием для классификации СИ по разрядам? Начнем с того, что в стандартах на образцовые термопары доверительная погрешность вообще не рассчитывается. Стандарт на образцовые термометры ГОСТ Р 8.571-98 вводит расчет доверительной погрешности как СКО среднего арифметического из трех измерений в реперной точке, приведенное к интервальной оценке с помощью коэффициента Стьюдента. В низкотемпературной области в формулу включена также инструментальная добавка от погрешности измерительной аппаратуры. Можно ли считать, что такая оценка точности характеризует сам термометр? Скорее она характеризует процесс измерения (в основном воспроизводимость температуры реперной точки). Без сомнения, если применить расчет расширенной неопределенности, включающий все возможные влияющие факторы, то мы получим более полную оценку точности результата измерения. Однако, что касается свойств термометра, то даже в такой оценке будет задействована только кратковременная стабильность сопротивления в течение трех измерительных циклов. А ведь она может быть достаточно хорошей как для образцовых, так и для рабочих ТС. Поэтому, следуя данной методике поверки практически из любого ТС можно сделать образцовый термометр, измеряя его сопротивление на прецизионной установке. Получается, что критерий доверительной погрешности не может применяться для разделения термометров и термопар на разряды.

Какая характеристика является определяющей и крайне желательной для образцового СИ при условии его индивидуальной градуировки? Если спросить специалистов поверочных центров то ответ будет: стабильность его индивидуальной градуировочной зависимости за межповерочный интервал в условиях ежедневного термоциклирования. Три цикла градуировки, выполняемые при поверке, не могут быть гарантией сохранения стабильности характеристики в течение года!

Все, что сказано выше кажется очевидным. Почему же никаких изменений в направлении нормирования характеристик образцовых СИ не происходит? Стандарты на технические требования и поверку образцовых СИ будут пересматриваться в ближайшее время. Хочется уже сейчас внести предварительные предложения для разработчиков новых редакций.
1) Нормировать в тех. требованиях стабильность термометра как минимум за 50 циклов охлаждение-нагрев рабочем диапазоне.
2) Нормировать долговременный дрейф характеристики как минимум за 100 ч. выдержки при верхнем пределе температур.
3) При поверке взять за основу расчет расширенной неопределенности результата с формированием полного бюджета входящих стандартных неопределенностей.
4) В бюджет включать стандартную неопределенность, характеризующую дрейф характеристики СИ за межповерочный интервал, определенный по данным предыдущей поверки.
В этом случае расширенная неопределенность будет характеризовать точность конкретного термометра и может быть выбрана как критерий классификации термометров по разрядам в поверочной схеме.
Я предвижу, что многие образцовые термометры сопротивления по этому критерию будут браковаться. Особенно ТС, изготовленные на основе рабочих ЧЭ. С одной стороны это удобно, иметь вибропрочный термометр повышенной точности для использования в термостатах для градуировки рабочих ТС. С другой стороны, конструкция ЧЭ (как правило, это спираль в каналах, заполненных оксидом алюминия) не выдерживает длительные тепловые циклы, и термометр сильно дрейфует. Производство образцовых ТС из рабочих ЧЭ не оптимальный вариант. Фирмы-производители таких СИ должны работать над новой конструкцией ЧЭ.

Недавно в каталоге одной иностранной фирмы я видела целую серию термометров повышенной точности на разные диапазоны температур и с разными защитными корпусами. Метрологические характеристики, нормируемые для таких ТС две: долговременная стабильность сопротивления (за 100 ч) и стабильность при циклическом изменении температуры (50 циклов). Фирма также приводит неопределенность поверки ТС, но уже не как характеристику термометра, а скорее как характеристику своего собственного конкретного оборудования. Для некоторых видов ТС приводится комбинированная оценка – стабильность плюс неопределенность поверки.

Образцовые термометры и термопары используются в каждой поверочной лаборатории для передачи размера единицы температуры рабочим СИ. Излишне говорить, что от их качества зависит точность измерения температуры в научных исследованиях, в быту, на энергетических узлах учета, на производстве, в том числе на особо важных объектах, атомных станциях, реакторах и т.д. Вопрос о точности образцовых СИ, их применении и поверке является важным для всех нас.

Приглашаю специалистов и всех посетителей сайта к дискуссии по поводу качества образцовых СИ и нормирования их характеристик. Все Ваши мнения, замечания, статьи по этой теме будут незамедлительно публиковаться на сайте.

Гл. редактор сайта Моисеева Наталия Павловна

Источник

Неопределенность измерений в метрологии

Определения погрешности и неопределенности измерений.

История возникновения термина «неопределенность измерений».

Термины используемые при расчете неопределенности.

Соотношение терминов теории неопределенности с терминами классической теории точности (в скобках):

Подробно о типах определённости и их расчётах рассказано в статье «Понятие и типы неопределенностей. ГОСТ 34100.3-2017»

Оценка результата измерений в терминах «погрешность измерений».

Рис.1. Диапазон возможных значений при погрешности

Оценка результата измерений в терминах «неопределенность измерений».

Рис.2. Диапазон возможных значений при неопределенности

Рис.3. Интервал значений при расчете неопределенности

Расчёт неопределённости с применением приборов.

В следующей статье «Расчет неопределенности результатов измерений | пример для люксметра «еЛайт»» мы рассмотрим практический пример как вручную вычислить неопределенность измерений освещенности, используя люксметр-пульсметр-яркомер еЛайт02. В некоторых современных приборах такой расчёт неопределённости уже осуществляется автоматически, как, например, в самом доступном люксметре с поверкой еЛайт-мини.

Рис.4. Профессиональный измеритель освещённости еЛайт01 с функцией автоматического расчёта неопределённости измерений.

Рис.5. Термоанемометр-гигрометр-барометр ЭкоТерма Максима 01 с функцией автоматического расчёта неопределённости измерений.

Выводы.

Отличие понятия «погрешности» от «неопределенности»:

Понравился материал? Поделитесь им в соцсетях:

Источник

Оценка погрешностей результатов измерений

Оценка погрешностей результатов измерений

Погрешности измерений и их типы

Любые измерения всегда производятся с какими-то погрешностями, связанными с ограниченной точностью измерительных приборов, неправильным выбором, и погрешностью метода измерений, физиологией экспериментатора, особенностями измеряемых объектов, изменением условий измерения и т. д. Поэтому в задачу измерения входит нахождение не только самой величины, но и погрешности измерения, т. е. интервала, в котором вероятнее всего находится истинное значение измеряемой величины. Например, при измерении отрезка времени t секундомером с ценой деления 0,2 с можно сказать, что истинное значение его находится в интервале от с до с. Таким образом, измеряемая величина всегда содержит в себе некоторую погрешность , где и X – соответственно истинное и измеренное значения исследуемой величины. Величина называется абсолютной погрешностью (ошибкой) измерения, а выражение , характеризующее точность измерения, называется относительной погрешностью.

Вполне естественно стремление экспериментатора произвести всякое измерение с наибольшей достижимой точностью, однако такой подход не всегда целесообразен. Чем точнее мы хотим измерить ту ил иную величину, тем сложнее приборы мы должны использовать, тем больше времени потребуют эти измерения. Поэтому точность окончательного результата должна соответствовать цели проводимого эксперимента. Теория погрешностей дает рекомендации, как следует вести измерения и как обрабатывать результаты, чтобы величина погрешности была минимальной.

Все возникающие при измерениях погрешности обычно разделяют на три типа – систематические, случайные и промахи, или грубые ошибки.

Систематические погрешности обусловлены ограниченной точностью изготовления приборов (приборные погрешности), недостатками выбранного метода измерений, неточностью расчетной формулы, неправильной установкой прибора и т. д. Таким образом, систематические погрешности вызываются факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений. Величина этой погрешности систематически повторяется либо изменяется по определенному закону. Некоторые систематические ошибки могут быть исключены (на практике этого всегда легко добиться) путем изменения метода измерений, введение поправок к показаниям приборов, учета постоянного влияния внешних факторов.

Хотя систематическая (приборная) погрешность при повторных измерениях дает отклонение измеряемой величины от истинного значения в одну сторону, мы никогда не знаем в какую именно. Поэтому приборная погрешность записывается с двойным знаком

Случайные погрешности вызываются большим числом случайных причин (изменением температуры, давления, сотрясения здания и т. д.), действия которых на каждое измерение различно и не может быть заранее учтено. Случайные погрешности происходят также из-за несовершенства органов чувств экспериментатора. К случайным погрешностям относятся и погрешности обусловленные свойствами измеряемого объекта.

Исключить случайны погрешности отдельных измерений невозможно, но можно уменьшить влияние этих погрешностей на окончательный результат путем проведения многократных измерений. Если случайная погрешность окажется значительно меньше приборной (систематической), то нет смысла дальше уменьшать величину случайной погрешности за счет увеличения числа измерений. Если же случайная погрешность больше приборной, то число измерений следует увеличить, чтобы уменьшить значение случайной погрешности и сделать ее меньше или одного порядка с погрешностью прибора.

2. Оценка систематической (приборной) погрешности

При прямых измерениях значение измеряемой величины отсчитывается непосредственно по шкале измерительного прибора. Ошибка в отсчете может достигать нескольких десятых долей деления шкалы. Обычно при таких измерениях величину систематической погрешности считают равной половине цены деления шкалы измерительного прибора. Например, при измерении штангенциркулем с ценой деления 0,05 мм величина приборной погрешности измерения принимают равной 0,025 мм.

Цифровые измерительные приборы дают значение измеряемых ими величин с погрешностью, равной значению одной единицы последнего разряда на шкале прибора. Так, если цифровой вольтметр показывает значение20,45 мВ, то абсолютная погрешность при измерении равна мВ.

Систематические погрешности возникают и при использовании постоянных величин, определяемых из таблиц. В подобных случаях погрешность принимается равной половине последнего значащего разряда. Например, если в таблице значение плотности стали дается величиной, равной 7,9∙103 кг/м3, то абсолютная погрешность в этом случае равна кг/м3.

Некоторые особенности в расчете приборных погрешностей электроизмерительных приборов будут рассмотрены ниже.

При определении систематической (приборной) погрешности косвенных измерений функциональной величины используется формула

, (1)

где — приборные ошибки прямых измерений величины , — частные производные функции по переменной .

В качестве примера, получим формулу для расчета систематической погрешности при измерении объема цилиндра. Формула вычисления объема цилиндра имеет вид

.

Частные производные по переменным d и h будут равны

, .

Таким образом, формула для определения абсолютной систематической погрешности при измерении объема цилиндра в соответствии с имеет следующий вид

,

где и приборные ошибки при измерении диаметра и высоты цилиндра

3. Оценка случайной погрешности.

Доверительный интервал и доверительная вероятность

Для подавляющего большинства простых измерений достаточно хорошо выполняется так называемый нормальный закон случайных погрешностей (закон Гаусса), выведенный из следующих эмпирических положений.

1) погрешности измерений могут принимать непрерывный ряд значений;

2) при большом числе измерений погрешности одинаковой величины, но разного знака встречаются одинаково часто,

3) чем больше величина случайной погрешности, тем меньше вероятность ее появления.

График нормального закона распределения Гаусса представлен на рис.1. Уравнение кривой имеет вид

, (2)

где — функция распределения случайных ошибок (погрешностей), характеризующая вероятность появления ошибки , σ – средняя квадратичная ошибка.

Величина σ не является случайной величиной и характеризует процесс измерений. Если условия измерений не изменяются, то σ остается постоянной величиной. Квадрат этой величины называют дисперсией измерений. Чем меньше дисперсия, тем меньше разброс отдельных значений и тем выше точность измерений.

Точное значение средней квадратичной ошибки σ, как и истинное значение измеряемой величины, неизвестно. Существует так называемая статистическая оценка этого параметра, в соответствии с которой средняя квадратичная ошибка равняется средней квадратичной ошибке среднего арифметического . Величина которой определяется по формуле

, (3)

где — результат i-го измерения; — среднее арифметическое полученных значений; n – число измерений.

Чем больше число измерений, тем меньше и тем больше оно приближается к σ. Если истинное значение измеряемой величины μ, ее среднее арифметическое значение, полученное в результате измерений , а случайная абсолютная погрешность , то результат измерений запишется в виде .

Интервал значений от до , в который попадает истинное значение измеряемой величины μ, называется доверительным интервалом. Поскольку является случайной величиной, то истинное значение попадает в доверительный интервал с вероятностью α, которая называется доверительной вероятностью, или надежностью измерений. Эта величина численно равна площади заштрихованной криволинейной трапеции. (см. рис.)

Все это справедливо для достаточно большого числа измерений, когда близка к σ. Для отыскания доверительного интервала и доверительной вероятности при небольшом числе измерений, с которым мы имеем дело в ходе выполнения лабораторных работ, используется распределение вероятностей Стьюдента. Это распределение вероятностей случайной величины , называемой коэффициентом Стьюдента, дает значение доверительного интервала в долях средней квадратичной ошибки среднего арифметического .

. (4)

Распределение вероятностей этой величины не зависит от σ2, а существенно зависит от числа опытов n. С увеличением числа опытов nраспределение Стьюдента стремится к распределению Гаусса.

Функция распределения табулирована (табл.1). Значение коэффициента Стьюдента находится на пересечении строки, соответствующей числу измерений n, и столбца, соответствующего доверительной вероятности α

Источник