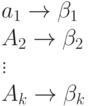Что такое длина кодовых слов

Информационные технологии

Неравномерное кодирование. Средняя длина кодирования

В приведенных выше примерах кодирования все кодовые слова имели одинаковую длину. Однако это не является обязательным требованием. Более того, если вероятности появления сообщений заметно отличаются друг от друга, то сообщения с большой вероятностью появления лучше кодировать короткими словами, а более длинными словами кодировать редкие сообщений. В результате кодовый текст при определенных условиях станет в среднем короче.

Наиболее экономным является код с наименьшей средней длиной 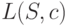. Сравним на примерах экономичность различных способов кодирования одного и того же источника.

Пусть источник содержит 4 сообщения с вероятностями . Эти сообщения можно закодировать кодовыми словами постоянной длины, состоящими из двух знаков, в алфавите в соответствии с кодовой таблицей.

	00
	01
A_3	10
A_4	11

Очевидно, что для представления (передачи) любой последовательности в среднем потребуется 2 знака на одно сообщение. Сравним эффективность такого кодирования с описанным выше кодированием словами переменной длины. Кодовая таблица для данного случая может иметь следующий вид.

	0
	1
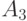	10
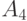	11

В этой таблице, в отличие от предыдущей, наиболее частые сообщения и кодируются одним двоичным знаком. Для последнего варианта кодирования имеем

в то время как для равномерного кода средняя длина (она совпадает с общей длиной кодовых слов). Из рассмотренного примера видно, что кодирование сообщений словами различной длины может дать суще-ственное (почти в два раза) увеличение экономичности кодирования.

Необходимо отметить, что неоднозначность декодирования слова появилась несмотря на то, что условие однозначности декодирования знаков (инъективность кодового отображения) выполняется.

Решение данной проблемы заключается в том, чтобы иметь возможность в любом кодовом тексте выделять отдельные кодовые слова без использования специальных разделительных знаков. Иначе говоря, необходимо, чтобы код удовлетворял следующему требованию: всякая последовательность кодовых знаков может быть единственным образом разбита на кодовые слова. Коды, для которых последнее требование выполнено, называются однозначно декодируемыми (иногда их называют кодами без запятой).

Рассмотрим код (схему алфавитного кодирования) , заданный кодовой таблицей

и различные слова, составленные из элементарных кодов.

Определение. Код называется однозначно декодируемым, если

Если таблица кодов содержит одинаковые кодовые слова, то есть если

то код заведомо не является однозначно декодируемым (схема не является разделимой). Такие коды далее не рассматриваются.

Префиксные коды

Наиболее простыми и часто используемыми кодами без специального разделителя кодовых слов являются так называемые префиксные коды [29].

Теорема 1. Префиксный код является однозначно декодируемым.

Множество кодовых слов можно графически изобразить как поддерево словарного дерева (рис.6.5). Для этого из всего словарного дерева следует показать только вершины, соответствующие кодовым словам, и пути, ведущие от этих вершин к корню дерева. Такое поддерево называют деревом кода или кодовым деревом.

Замечание. Свойство префиксности является достаточным, но не является необходимым для однозначной декодируемости.

Если код префиксный, то, читая кодовую запись подряд от начала, мы всегда сможем разобраться, где кончается одно кодовое слово и начинается следующее. Если, например, в кодовой записи встретилось кодовое обозначение 110, то разночтений быть не может, так как в силу префиксности наш код не содержит кодовых обозначений 1, 11 или, скажем, 1101. Именно так обстояло дело для рассмотренного выше кода, который очевидно является префиксным.

Источник

Основы кодирования

Дата добавления: 2013-12-23 ; просмотров: 5174 ; Нарушение авторских прав

Связь и кодирование. Равномерные и неравномерные коды. Проблемы декодирования, условие Фано. Количество и объем информации. Избыточность кода.

Связь и кодирование. Появление технических средств связи повлекло за собой создание методов кодирования сообщений. Передача информации по техническим каналам связи оказалась возможной лишь для сообщений, представленных в строго определенном виде – в закодированном. Основной задачей теории и практики кодирования становится разработка методов преобразования информации, удовлетворяющих современным техническим средствам ее передачи.

Еще в древности люди умели передавать сигналы на расстояние с помощью огня. Однако считается, что современные очертания связь приобрела с появлением оптического телеграфа, изобретенного К. Шаппом (1791 г.). Решающим этапом в процессе развития связи явилось изобретение С. Морзе телеграфного аппарата (1837 г.), а затем и азбуки Морзе. Это изобретение актуально до сих пор, так как оно основано на двоичном кодировании, которое просто смоделировать физически: «1» – есть электрический ток, «0» – нет тока.

Дальнейшее усовершенствование телеграфного аппарата, а также прокладка межконтинентальных кабелей завершились появлением коммерческого телеграфа и сертификацией международного телеграфного кода. Там, где невозможно было использовать провода, по-прежнему оказались необходимы оптические средства связи, такие как международный флажковый код, изобретенный капитаном Ф. Марьятом (1817 г.), а также семафоры и светофоры, до сих пор применяющиеся на железных дорогах. Изобретение радио Поповым и Маркони избавило связь от проводов. А с изобретением телевидения (1935 г.) развитие средств связи временно стабилизируется.

Теория кодирования всё это время развивается с двух направлений. Первое – это создание двоичных кодов с особыми свойствами, полезными с технической точки зрения. К ним можно отнести циклические и одношаговые коды Ж. Бодо (1889 г.), помехоустойчивые коды ван Дуурена (1937 г.) и код Р. Хемминга (1950 г.), позволяющий обнаруживать и исправлять некоторые ошибки, возникающие при передаче сообщений. Второе – это обеспечение криптографической надежности сообщений, особенно актуальное в годы Второй мировой войны. Занимаясь решением этой задачи, Клод Шеннон (1948 г.) и создал теорию (количества) информации. В серии работ он рассмотрел вопросы оптимального кодирования, а также передачи информации при наличии помех.

Получившие свое начало в области связи методы кодирования обретают особую актуальность с появлением вычислительных машин. Любая информация в компьютере представлена в закодированном виде, причем многообразие ее носителей (оперативная память, магнитные диски, дисплей и т. д.) предполагают разнообразие информационных кодов. Кроме того, важнейшей задачей теории кодирования становится проблема сжатия информации с целью ее хранения, восстановления в случае отказов, и увеличения скорости передачи на расстояние.

Итак, перейдем к основным понятиям теории кодирования.

Кодированиембудем считать процесс отображения одного набора знаков в другой, а кодом – множество образов при этом отображении.

При кодировании используются два алфавита: исходный A = <a₁, a₂,…,a_N> и кодовый B = <b₁, b₂,…,b_M>. Обычно N > M. Кодирование заключается в записи символов исходного алфавита А с помощью символов кодового алфавита В. Каждому символу алфавита А ставится в соответствие некоторая последовательность символов алфавита В, называемая кодом или кодовым словом. Число символов в кодовом слове называется длиной кодового слова. Коды бывают двух типов: равномерные – когда длина всех кодовых слов (или их разрядность) одинакова, и неравномерные – когда кодовые слова имеют разную длину.

Равномерные кодыхарактеризуются минимальной разрядностью кодовых слов, которая рассчитывается по формуле

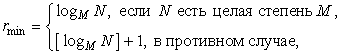(3.1)

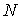
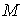
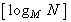
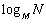
где – объем исходного алфавита А;

– объем кодового алфавита В;

означает целую часть числа .

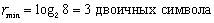
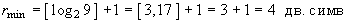
Рассмотрим эти формулы для случая двоичного кодирования (т. е. при М = 2). Минимальная разрядность равномерного кода для алфавита объемом 8 символов будет равна . А для 9-бук-венного алфавита .

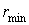
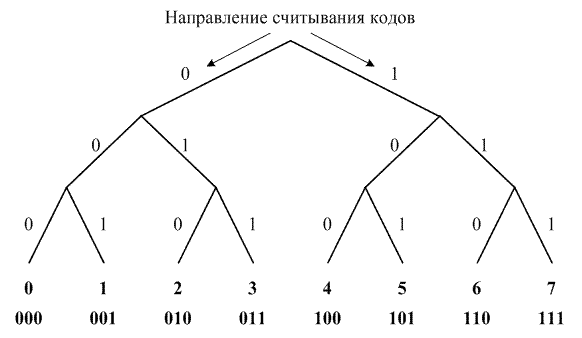
Нетрудно заметить, что есть целое число. В большинстве случаев за счет округления числа H(A) до целого, что порождает избыточность кода, о которой будет сказано далее.

Рис. 3.1. Равномерное двоичное кодирование путем построения дерева

Если кодовый алфавит состоит из двух символов В = <0, 1>, то, как уже отмечалось, такое кодирование называется двоичным. Двоичный равномерный код легко получить путем построения двоичного дерева. Пусть исходный алфавит A = <0, 1, 2, 3, 4, 5, 6, 7>насчитывает 8 символов, тогда двоичное дерево для кодирования его символов будет иметь вид, представленный на рис. 3.1. Код каждого символа исходного алфавита считывается с дерева, двигаясь от корня к листьям, и состоит из 3 символов кодового.

По формуле (3.3) можно найти количество информации, содержащееся в кодовом слове: 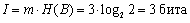. Мы видим, что двоичный код содержит столько бит информации, сколько нулей и единиц в нем содержится.

Результаты рассмотренных двух способов кодирования совпадают, если обозначать ветви кодового дерева слева направо в соответствии с порядком букв в алфавите B.

Декодирование сообщений, составленных в равномерном коде, не представляет сложности. Достаточно считывать символы сообщения группами по r символов и сопоставлять их с таблицей кодов.

Неравномерные кодыхарактеризуются средней длиной кодового слова

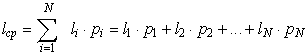(3.2)

– объем исходного алфавита.

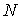
Например, если алфавит А = <a, b, c, d, e> с вероятностями появления символов в сообщениях (p_a = 0,5; p_b = 0,2; p_c = 0,1; p_d = 0,15; p_e = 0,05) закодирован двоичным неравномерным кодом (a – 0; b – 10; c – 1110; d – 110; e – 1111), то средняя длина кодового слова для такого алфавита будет

.

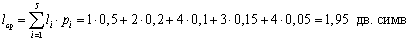
Таким образом, средняя длина кодового слова есть сумма длин всех кодовых слов, взятых с весом, равным вероятности появления кодируемого символа.

В отличие от равномерного кода, при котором декодирование не представляет проблемы, неравномерный код требует специальных мер для обеспечения правильного и однозначного декодирования сообщений. Простейший способ – ввести разделитель между отдельными кодовыми словами, зарезервировав для этого либо один символ кодового алфавита, либо кодовую последовательность. Однако это ведет к увеличению нагрузки на канал связи, так как сообщение увеличивается по объему. На практике разделимые неравномерные коды строятся на основе соблюдения условия Фано, или принципа префиксности.

Условие Фано. Для того чтобы неравномерный код был однозначно и правильно декодируем, достаточно при его построении обеспечить выполнение следующего условия: никакое кодовое слово не должно быть началом никакого другого кодового слова.

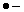
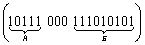
Приведем пример применения разделителя. Так, в азбуке Морзе символ А имеет код ( ), символ Б – (). В современных средствах связи символы азбуки Морзе представлены своими двоичными эквивалентами () – 1; ( –) – 111. Пауза между точками и тире обозначается нулем. Разделитель между буквами – три нуля (000). Так сообщение АБ ()() будет иметь вид

.

Мы видим, что разделитель позволяет надежно отличать один символ от другого.

Несмотря на сложности декодирования, следует подчеркнуть, что применение неравномерных кодов позволяет добиться того, что средняя длина кодового слова 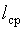будет меньше, чем минимальная разрядность при кодировании того же алфавита равномерным кодом. Это дает преимущество неравномерному коду с точки зрения избыточности.

Источник

Основные методы кодирования данных (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6

Пример. 3 Код из примера 1 не является разделимым, поскольку кодовое слово 010010 может быть декодируемо двумя способами: a3a3 или a2a1a2.

Побуквенный код называется префиксным, если в его множестве кодовых слов ни одно слово не является началом другого, т. е. элементарный код одной буквы не является префиксом элементарного кода другой буквы.

Пример 4. Код из примера 1 не является префиксным, поскольку элементарный код буквы a2 является префиксом элементарного кода буквы a3.

Утверждение. Префиксный код является разделимым.

Заметим, что разделимый код может быть не префиксным.

Приведем основные теоремы побуквенного кодирования.

Теорема (Крафт). Для того, чтобы существовал побуквенный двоичный префиксный код с длинами кодовых слов L1,…,Ln необходимо и достаточно, чтобы

.

Доказательство. Докажем необходимость. Пусть существует префиксный код с длинами L1,…,Ln. Рассмотрим полное двоичное дерево. Каждая вершина закодирована последовательностью нулей и единиц (как показано на рисунке).

Рисунок 2 Полное двоичное дерево с помеченными вершинами

В этом дереве выделим вершины, соответствующие кодовым словам. Тогда любые два поддерева, соответствующие кодовым вершинам дерева, не пересекаются, т. к. код префиксный. У i-того поддерева на r-том уровне – 2r—Li вершин. Всего вершин в поддереве 2r. Тогда, , .

Докажем достаточность утверждения. Пусть существует набор длин кодовых слов такой, что . Рассмотрим полное двоичное дерево с помеченными вершинами. Пусть длины кодовых слов упорядочены по возрастанию L1≤ L2≤ … ≤ Ln. Выберем в двоичном дереве вершину V1 на уровне L1. Уберем поддерево с корнем в вершине V1. В оставшемся дереве возьмем вершину V2 на уровне L2 и удалим поддерево с корнем в этой вершине и т. д. Последовательности, соответствующие вершинам V1, V2,…, Vn образуют префиксный код. Теорема доказана.

Пример 6. Построить префиксный код с длинами L1=1, L2=2, L3=2 для алфавита A=<a1,a2,a3>. Проверим неравенство Крафта для набора длин

.

Неравенство выполняется и, следовательно, префиксный код с таким набором длин кодовых слов существует. Рассмотрим полное двоичное дерево с 23 помеченными вершинами и выберем вершины дерева, как описано выше. Тогда элементарные коды могут быть такими: a1 ®0, a2®10, a3 ®11.

Рисунок 3 Построение префиксного кода с заданными длинами

Процесс декодирования выглядит следующим образом. Просматриваем полученное сообщение, двигаясь по дереву. Если попадем в кодовую вершину, то выдаем соответствующую букву и возвращаемся в корень дерева и т. д.

Теорема (МакМиллан). Для того чтобы существовал побуквенный двоичный разделимый код с длинами кодовых слов L1,…,Ln , необходимо и достаточно, чтобы .

Доказательство. Покажем достаточность. По теореме Крафта существует префиксный код с длинами L1,…,Ln, и он является разделимым.

Докажем необходимость утверждения. Рассмотрим тождество

Положим . Тогда тождество можно переписать следующим образом

,

где , – число всевозможных представлений числа j в виде суммы . Сопоставим каждому представлению числа j в виде суммы последовательность нулей и единиц длины j по следующему правилу

,

где bs – элементарный код длины s. Тогда различным представлениям числа j будут соответствовать различные кодовые слова, поскольку код является разделимым. Таким образом, и . Используя предельный переход получим при . Теорема доказана.

Пример 7. Азбука Морзе – это схема алфавитного кодирования

A®01, B®1000, C®1010, D®100, E®0, F®0010, G®110, H®0000, I®00, J®0111, K®101, L®0100, M®11, N®10, O®111, P®0110, Q®1101, R®010, S®000, T®1, U®001, V®0001, W®011, X®1001, Y®1011, Z®1100.

Неравенство МакМиллана для азбуки Морзе не выполнено, поскольку

Следовательно, этот код не является разделимым. На самом деле в азбуке Морзе имеются дополнительные элементы – паузы между буквами (и словами), которые позволяют декодировать сообщение. Эти дополнительные элементы определены неформально, поэтому прием и передача сообщений (особенно с высокой скоростью) является некоторым искусством, а не простой технической процедурой.

5. оптимальное ПОБУКВЕННОЕ кодирование

5.1 Основные понятия

При кодировании сообщений считается, что символы сообщения порождаются некоторым источником информации. Источник считается заданным полностью, если дано вероятностное описание процесса появления сообщений на выходе источника. Это означает, что в любой момент времени определена вероятность порождения источником любой последовательности символов Р(x1x2x3. xL), L≥1. Такой источник называется дискретным вероятностным источником.

Для другого класса источников (марковских) существует статистическая взаимосвязь между порождаемыми символами. В дальнейшем мы будем рассматривать кодирование стационарных (с неизменным распределением вероятностей) бернуллиевских дискретных источников без памяти.

Пусть имеется дискретный вероятностный источник без памяти, порождающий символы алфавита А=<a1,…,an> с вероятностями , . Основной характеристикой источника является энтропия, которая представляет собой среднее значение количества информации в сообщении источника и определяется выражением (для двоичного случая)

.

Энтропия характеризует меру неопределенности выбора для данного источника.

Пример. Если А=<a1,a2>, p1=0, p2 =1, т. е. источник может породить только символ a2, то неопределенности нет, энтропия H(p1,p2)=0.

Источник с равновероятными символами А=<a1,a2>, p1 =1/2, p2 =1/2, будет иметь максимальную энтропию H(p1,p2)=1.

Величина называется энтропией на символ последовательности длины L, где AL — множество всех последовательностей длины L в алфавите A, x=(x1,x2. xL) — последовательность L букв дискретного cтационарного источника. Обозначим через предел энтропии HL при L® ¥ . Эту величину называют предельной энтропией источника. Показано, что для стационарного бернуллиевского источника

.

Для практических применений важно, чтобы коды сообщений имели по возможности наименьшую длину. Основной характеристикой неравномерного кода является количество символов, затрачиваемых на кодирование одного сообщения. Пусть имеется разделимый побуквенный код для источника, порождающего символы алфавита А=<a1,…,an> с вероятностями pi =P(ai), состоящий из n кодовых слов с длинами L1,…,Ln в алфавите <0,1>. Средней длиной кодового слова называется величина , которая показывает среднее число кодовых букв на одну букву источника.

Пример. Пусть имеются два источника с одним и тем же алфавитом А=<a1,a2,a3> и разными вероятностными распределениями P1=<1>, P2=<1>, которые кодируются одним и тем же кодом

.

Средняя длина кодового слова для разных источников будет различной

Побуквенный разделимый код называется оптимальным, если средняя длина кодового слова минимальна среди всех побуквенных разделимых кодов для данного распределения вероятностей символов.

Избыточностью кода называется разность между средней длиной кодового слова и предельной энтропией источника сообщений

Избыточность кода является показателем качества кода, оптимальный код обладает минимальной избыточностью. Задача эффективного неискажающего сжатия заключается в построении кодов с наименьшей избыточностью, у которых средняя длина кодового слова близка к энтропии источника. К таким кодам относятся классические коды Хаффмана, Шеннона, Фано, Гилберта-Мура и арифметический код.

Взаимосвязь между средней длиной кодового слова и энтропией дискретного вероятностного источника при побуквенном кодировании выражает следующая теорема.

Теорема 1 (Шеннон). Для источника с алфавитом А=<a1,…,an> и вероятностями pi =P(ai), и любого разделимого побуквенного кода средняя длина кодового слова всегда не меньше энтропии

и можно построить разделимый побуквенный код, у которого средняя длина кодового слова превосходит энтропию не больше, чем на единицу:

Lcp 0 можно выбрать достаточно большое L, чтобы величина Lcp удовлетворяла неравенствам:

,

и левое неравенство для Lcp никогда не нарушается для разделимого кода.

Приведем некоторые свойства, которыми обладает любой оптимальный побуквенный код.

Доказательство (от противного): Пусть есть i и j, что Li>Lj при pi>pj. Тогда

т. е. если поменяем местами Li и Lj, то получим код, имеющий меньшую среднюю длину кодового слова, что противоречит с оптимальности кода. Лемма 1 доказана.

Лемма 2 Пусть – схема оптимального префиксного кодирования для распределения вероятностей Р, . Тогда среди элементарных кодов, имеющих максимальную длину, существуют два, которые различаются только в последнем разряде.

Доказательство. Покажем, что в оптимальной схеме кодирования всегда найдется два кодовых слова максимальной длины. Предположим обратное. Пусть кодовое слово максимальной длины одно и имеет вид , . Тогда длина любого элементарного кода не больше длины b, т. е. , . Поскольку схема кодирования префиксная, то кодовые слова не являются префиксом b. С другой стороны, b не является префиксом кодовых слов . Таким образом, новая схема кодирования также является префиксной, причем с меньшей средней длиной кодового слова , что противоречит оптимальности исходной схемы кодирования. Пусть теперь два кодовых слова и максимальной длины отличаются не в последнем разряде, т. е. , , , . Причем , не являются префиксами для других кодовых слов и наоборот. Тогда новая схема также является префиксной, причем , что противоречит оптимальности исходной схемы кодирования. Лемма 2 доказана.

5.2 Оптимальный код Хаффмана

Метод оптимального побуквенного кодирования был разработан в 1952 г. Д. Хаффманом. Оптимальный код Хаффмана обладает минимальной средней длиной кодового слова среди всех побуквенных кодов для данного источника с алфавитом А=<a1,…,an> и вероятностями pi =P(ai).

Рассмотрим алгоритм построения оптимального кода Хаффмана, который основывается на утверждениях лемм предыдущего параграфа.

Здесь символы источника уже упорядочены в соответствии с их вероятностями. Будем складывать две наименьшие вероятности и включать суммарную вероятность на соответствующее место в упорядоченном списке вероятностей до тех пор, пока в списке не останется два символа. Тогда закодируем эти два символа 0 и 1. Далее кодовые слова достраиваются, как показано на рисунке 4.

Источник