Что такое длина деления шкалы

Длина деления шкалы

2.8. Длина деления шкалы

По title=»ГСИ. Метрология. Основные термины и определения»

Смотреть что такое «Длина деления шкалы» в других словарях:

длина деления шкалы — Расстояние между осями (или центрами) двух соседних отметок шкалы, измеренное вдоль воображаемой линии, проходящей через середины самых коротких отметок шкалы. [РМГ 29 99] EN scale spacing length of a scale division distance between two… … Справочник технического переводчика

длина деления шкалы — skalės padalos ilgis statusas T sritis Standartizacija ir metrologija apibrėžtis Atstumas tarp dviejų gretimų skalės žymių, išmatuotas išilgai įsivaizduojamos linijos, einančios per trumpiausių žymių centrus. atitikmenys: angl. scale spacing;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

длина деления шкалы — skalės padalos ilgis statusas T sritis Standartizacija ir metrologija apibrėžtis Atstumas tarp dviejų gretimų žymių, išmatuotas išilgai tos pačios linijos kaip ir skalės ilgio atveju. atitikmenys: angl. scale spacing; scale spacing length of a… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

длина деления шкалы — skalės padalos ilgis statusas T sritis fizika atitikmenys: angl. scale spacing vok. Abstand der Teilungsmarken, m; Teilstrichabstand, m rus. длина деления шкалы, f pranc. longueur d’une division d’échelle, f … Fizikos terminų žodynas

длина — 3.1 длина (length) l: Наибольший линейный размер лицевой грани измеряемого образца. Источник: ГОСТ Р ЕН 822 2008: Изделия теплоизоляционные, применяемые в строительстве. Методы измерения длины и ширины … Словарь-справочник терминов нормативно-технической документации

Деления и делительная машина — Для практики наблюдательных наук правильные и точные Д., как линейные, так и угловые, представляют предмет первостепенной важности. Глаз или осязание дает нам лишь возможность судить о равенстве двух промежутков, когда они наложены или надлежащим … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

ДЕЛЕНИЕ ШКАЛЫ — отрезок шкалы между двумя соседними градуировочными отметками на аналоговой шкале. Д. ш. используется как единица счета для выражения показаний. При этом принимается во внимание, что индикаторная метка (указатель) начиная от нулевой отметки… … Энциклопедический словарь по психологии и педагогике

ГОСТ 29329-92: Весы для статического взвешивания. Общие технические требования — Терминология ГОСТ 29329 92: Весы для статического взвешивания. Общие технические требования оригинал документа: (Электронные весы) Термин «Электронные весы» применим к настольным весам Определения термина из разных документов: (Электронные весы)… … Словарь-справочник терминов нормативно-технической документации

Шкала средства измерений — Для термина «Шкала» см. другие значения. Шкала (лат. scala лестница) часть показывающего устройства средства измерений … Википедия

Abstand der Teilungsmarken — skalės padalos ilgis statusas T sritis Standartizacija ir metrologija apibrėžtis Atstumas tarp dviejų gretimų skalės žymių, išmatuotas išilgai įsivaizduojamos linijos, einančios per trumpiausių žymių centrus. atitikmenys: angl. scale spacing;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Источник

Шкала измерений — типы, предел, виды

Шкала измерений – это совокупность значений, позволяющих количественно или качественно отобразить свойства объекта измерений. Разнообразные проявления (количественные или качественные) любого свойства образуют множества, отображения элементов которых на упорядоченное множество чисел или в более общем случае условных знаков образуют шкалы измерения этих свойств. Шкала измерений количественного свойства является шкалой физической величины. Шкала физической величины — это упорядоченная последовательность значений ФВ, принятая по соглашению на основании результатов точных измерений.

Виды шкал измерений

В практической деятельности необходимо проводить измерения различных величин, характеризующих свойства тел, веществ, явлений и процессов. Некоторые свойства измерительных шкал в метрологии проявляются только качественно, другие — количественно.

Шкала – упорядоченный числовой или символьный ряд значений, отражающий допустимые вариации значений измеряемой величины.

В соответствии с логической структурой проявления свойств различают пять основных видов шкал измерений: шкалы наименований, шкалы порядка, шкалы интервалов, шкалы отношений, абсолютные шкалы.

Элементы шкалы

Интервал деления шкалы (деление шкалы) — расстояние между осями симметрии двух рядом лежащих штрихов (выражается в линейных или в угловых единицах)

ШКАЛЫ ИЗМЕРЕНИЙ

Шкала наименований – это качественная, а не количественная шкала, она не содержит нуля и единиц измерений (напр., шкала цветов).

Такие шкалы используется для классификации объектов, свойства которых проявляются только в отношении эквивалентности (совпадения или несовпадения). Эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида не являются шкалами ФВ. В шкалах наименований оценивание осуществляется с использованием органов чувств человека, наиболее адекватен результат, выбранный большинством экспертов. Поскольку данные шкалы характеризуются только отношениями эквивалентности, то в них отсутствуют понятия нуля, «больше или меньше» и единицы измерения.

Шкала порядка – характеризует значение измеряемой величины в баллах (напр., шкала землетрясений; силы ветра и др.).

Она является монотонно изменяющейся и позволяет установить отношения «больше — меньше» между величинами, характеризующими это свойство. Нуль существует или не существует, но принципиально невозможно ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нельзя судить, во сколько раз больше или меньше конкретные проявления свойства.

Шкала интервалов – имеет условное нулевое значение, а интервалы устанавливают по согласованию (напр., шкала времени, шкала длины).

Данные шкалы являются дальнейшим развитием шкал порядка. Шкала состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. К таким шкалам относится летоисчисление, температурные шкалы.

Шкала отношений – имеет естественное нулевое значение, а единица измерений устанавливается по согласованию, в зависимости от требования точности измерения (напр., шкала веса).

С формальной точки зрения эта шкала является шкалой интервалов с естественным началом отсчета. К значениям, полученным по шкале отношений, применимы все арифметические действия, что имеет большое значение при измерении ФВ.

Дата добавления: 2014-02-04; 15002; Опубликованный материал нарушает авторские права? | Защита персональных данных |

Не нашли то, что искали? Воспользуйтесь поиском:

Виды шкал средств измерений

Шкала порядка (рангов)

Если свойство данного эмпирического объекта проявляет себя в отношении эквивалентности и порядка по возрастанию или убыванию количественного проявления свойства, то для него может быть построена шкала порядка. Она является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство. В шкалах порядка существует или не существует нуль, но принципиально нельзя ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нет возможности судить во сколько раз больше или меньше конкретные проявления свойства.

В случаях, когда уровень познания явления не позволяет точно установить отношения, существующие между величинами данной характеристики, либо применение удобно и достаточно для практики, используют условные (эмпирические) шкалы порядка. Условная шкала — это шкала ФВ, исходные значения которой выражены в условных единицах. Пример шкалы порядка — шкала вязкости Энглера, 12-бальная шкала Бофорта для силы морского ветра.

Рисунок — Пример шкалы порядка (шкала Бофорта)

Широкое распространение получили шкалы измерений порядка с нанесенными на них реперными точками. К таким шкалам, например, относится шкала Мооса для определения твердости минералов, которая содержит 10 опорных (реперных) минералов с различными условными числами твердости: тальк – 1; гипс – 2; кальций – 3; флюорит – 4; апатит – 5; ортоклаз – 6; кварц – 7; топаз – 8; корунд – 9; алмаз – 10. Отнесение минерала к той или иной градации твердости осуществляется на основании эксперимента, который состоит в том, что испытуемый материал царапается опорным. Если после царапанья испытуемого минерала кварцем (7) на нем остается след, а после ортоклаза (6) — не остается, то твердость испытуемого материала составляет более 6, но менее 7. Более точного ответа в этом случае дать невозможно,

В условных шкалах одинаковым интервалам между размерами данной величины не соответствуют одинаковые размерности чисел, отображающих размеры. С помощью этих чисел можно найти вероятности, моды, медианы, квантили, однако их нельзя использовать для суммирования, умножения и других математических операция. Определение значения величин при помощи шкал порядка нельзя считать измерением, так как на этих шкалах не могут быть введены единицы измерения. Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным, о чем свидетельствует рассмотренный пример.

Свойства шкал

Неравномерная шкала омметра

Шкала интервалов (разностей)

Эти шкалы измерений в метрологии являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. Пример шкалы интервалов — летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.

Рисунок – Пример шкалы интервалов (Температурные шкалы Цельсия и Фаренгейта)

На шкале интервалов определены действия сложения и вычитания интервалов. Действительно, по шкале времени интервалы можно суммировать или вычитать и сравнивать, во сколько раз один интервал больше другого, но складывать даты каких-либо событий просто бессмысленно.

Задать шкалу практически можно двумя путями. При первом из них выбираются два значения Qо и Q1, величины, которые относительно просто реализованы физически. Эти значения называются опорными точками, или основными реперами, а интервал (Q1

Рисунок – Пример шкалы отношений

При втором пути задания шкалы единица воспроизводится непосредственно как интервал, его некоторая доля или некоторое число интервалов размеров данной величины, а начало отсчета выбирают каждый раз по-разному в зависимости от конкретных условий изучаемого явления. Пример такого подхода — шкала времени, в которой 1с = 9192631770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. За начало отсчета принимается начало изучаемого явления.

Шкала отношений

Шкала отношений описывает свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода — аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода — пропорциональные). Пример шкалы отношений — шкала массы (второго рода), термодинамической температуры (первого рода).

В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений, установленная по соглашению. С формальной точки зрения этот вид шкал измерений является шкалой интервалов с естественным началом отсчета. К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерений физических величин.

Рисунок – Пример абсолютной шкалы (шкала температур Кельвина)

Шкалы отношений — самые совершенные. Они описываются уравнением Q = q, где Q — ФВ, для которой строится шкала, — ее единица измерения, q — числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q2 = q1/.

Литература

Абсолютные шкалы

Абсолютные шкалы — это шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначное определение единицы измерения и не зависящие от принятой системы единиц измерения. Примером абсолютной шкалы могут стать шкалы с относительным величинам: коэффициенту усиления, ослабления и др. Для образования многих производных единиц в системе СИ используются безразмерные и счетные единицы абсолютных шкал.

Отметим, что шкалы наименований и порядка называют неметрическими (концептуальными), а шкалы интервалов и отношений — метрическими (материальными). Метрические и абсолютные шкалы относятся к разряду линейных. Практическая реализация шкал измерений в метрологии осуществляется путем стандартизации как самих шкал и единиц измерений, так и, в необходимых случаях, способов и условий их однозначного воспроизведения.

Изготовление измерительной шкалы своими руками

Видео о том, как самостоятельно сделать шкалу стрелочного прибора на примере изготовления шкалы амперметра.

Источник

Эксплуатационные характеристики средств измерений

В России, как и во многих странах, работающих в системе СИ, для средств измерения, выпускаемых серийно, приняты равномерные (линейные) шкалы, статические характеристики которых строятся по уравнениям прямой линии

, (2.10)

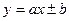
Если прямая линия проходит через начало координат, т.е. коэффициент b=0, уравнение (2.10) примет вид:

. (2.11)

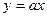
Рисунок 2.13 – Графики статических характеристик равномерных шкал СИ

Градуировочные характеристики таких шкал будут равны соответственно

, (2.12)

. (2.13)

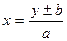
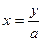
Линейные шкалы очень удобно настраивать по длине (изменяя коэффициент a) и нулевой отметке (изменяя коэффициент b).

Исключения отклонения от линейности, допускаются в отношении средств измерения расхода и количества жидких веществ, для которых применяются квадратические зависимости между входом и выходом:

(2.14)

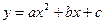
При нулевых значениях коэффициентов b и c соответственно имеем

. (2.15)

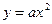
И, соответственно, градуировочные характеристики будут иметь вид

, (2.16)

, (2.17)

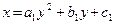
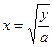
откуда следует, что и шкала и градуировочная характеристика средства измерения в этом случае будут неравномерными.

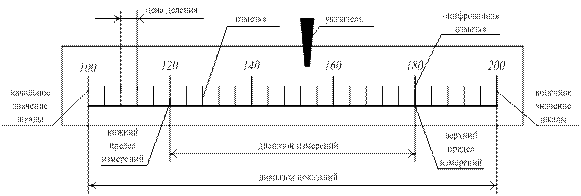
На примере равномерной шкалы, приведенной на рисунке 2.14, проиллюстрируем основные понятия, также относящиеся к эксплуатационным характеристикам средства измерения.

Рисунок 2.14 – Вид равномерной шкалы СИ

Пример — Для медицинского термометра начальным значением шкалы является 34,3 °С.

Пример — Для медицинского термометра конечным значением шкалы является 42 °С.

Значения величины, ограничивающие диапазон измерений снизу и сверху (слева и справа), называют соответственно нижним пределом или верхним пределом измерений.

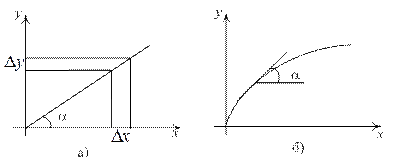
Графическое представление данного термина дано на рисунке 2.15,а.

а) линейная шкала, б) нелинейная шкала

Рисунок 2.15 – К определению чувствительности средства измерения

Различают абсолютную и относительную чувствительность.

Абсолютная чувствительность определяется формулой:

. (2.18)

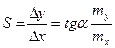
Относительная чувствительность по входу:

, (2.19)

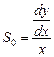
Если шкала неравномерная, то переходят к производным и чувствительность определяется как тангенс угла наклона касательной к статической характеристике в точке измерения (рисунок 2.16,б):

, (2.20)

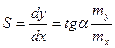
Величина, обратная чувствительности, называется постоянной средства измерения и вычисляется по формуле:

. (2.21)

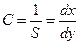
Иногда эту величину называют передаточным отношением и обозначают значком i (для технических приборов), в виде словесной формулы это выражается как

.

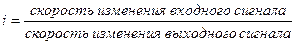
Чувствительность прибора, построенного по последовательной схеме преобразования, определяется произведением чувствительностей каждого звена, входящего в структурную схему. Для структурной схемы, изображенной на рисунке 2.8, можно записать

,

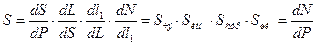
Чувствительность средства измерения имеет размерность, зависящую от характера измеряемой величины. Она может быть и безразмерной, если преобразуется однородная величина (ток в ток, длина в длину и т.д.).

Пример — Если самое незначительное изменение массы, которое вызывает перемещение стрелки весов, составляет 10 мг, то порог чувствительности весов равен 10 мг.

На практике применяются также термины: реагирование и порог реагирования, подвижность средства измерений и порог подвижности, срабатывание и порог срабатывания. Иногда применяют термин пороговая чувствительность. Это свидетельствует о том, что терминология для выражения понятий, связанных со свойствами средства измерений реагировать на малые изменения измеряемых величин, еще не устоялась. В целях упорядочения терминологии эти термины следует рассматривать как синонимы и не применять их.

Исходя из указанного определения, различают временное разрешение и пространственное разрешение.

Пример — Зона нечувствительности у судовой радиолокационной установки, зависящая от размеров судна и высоты антенны радиолокационной установки над судовыми надстройками.

Источник

Шкалы, координаты

Для определения размера какой-либо величины (длина, вес, температура и т.д.) мы используем измерительные приборы и инструменты со шкалами для отображения результата.

Шкала – это расположенный в определенной последовательности ряд отметок, которые соответствуют числовому значению измеряемой величины.

Например, в школьном курсе математики и геометрии для измерения длины геометрического объекта, в частности отрезка, используется линейка (рисунок 1).

Рисунок 1. Измерительная линейка.

Из урока Измерение величин вы уже знаете, что такое единица измерения, а их соотношения можете посмотреть в справочном разделе.

Деления шкалы – это равные части, на которые она разбита. Каждое деление шкалы обозначается отметками (черточками).

Нулевая отметка шкалы – это отметка, которая соответствует нулевому значению измеряемой нами величины.

Цена деления шкалы – это величина значения одного деления шкалы. То есть, это величина значения между двумя соседними отметками на шкале.

Как мы видим на рисунке 1, деления, обозначенные большими черточками, пронумерованы, и значение каждого такого деления равно 1 см. В этом легко убедиться, если найти разницу между значениями каждого из соседних делений: 1-0=1, 2-1=3, …, 9-8=1, 10-9=1.
Но каждое из больших делений разделено девятью маленькими черточками на 10 делений. Мы знаем, что в 1 см содержится 10 мм, поэтому разделив эти 10 мм на 10 делений, мы получим цену деления линейки, равную 1 мм.

Цена деления может отличаться не только у разных же измерительных приборов, но и у одних и тех же.

Рисунок 2 Цена деления шкалы

Например, на рисунке 2 изображены два термометра. Как вы думаете, они показывают одинаковую температуру, или нет?

Давайте посмотрим, так ли это? На левом термометре разница между двумя соседними пронумерованными отметками равна 10°C: 10-0=10, 20-10=10, и т.д. На правом же термометре эта разница равняется уже 20°C: 20-0=20, 40-20=20, и т.д. На обоих термометрах маленькие черточки делят одно большое пронумерованное деление на 10 частей. Разделив разницу между значениями пронумерованных отметок (10 и 20 соответственно) на количество делений между ними (10), мы получим цену деления каждого из термометров:

Итак, оба термометра показывают 20°C и еще два деления. Но на левом термометре это означает 20°C и еще два раза по 1°C, то есть, 20+2=22°C, а на правом – 20°C и еще два раза по 2°C, то есть, 20+4=24°C.

Координатный луч, единичный отрезок, координаты точки

Различные прямые линии со шкалами играют важную роль в школьной математике. Сейчас я познакомлю вас с одной из них.

Нарисуем точку O и проведем от нее направо луч. Обозначим направление луча стрелкой.

Рис. 3. Луч с началом в точке O

Рис. 4. Луч с равными отрезками

Поставим возле начала луча (точки O ) число 0 (нуль). Возле второго конца отрезка OP (возле точки P ) поставим число 1 (один). Таким образом мы обозначаем, что длина отрезка OP равна 1 (единице).

Аналогичным образом вы можете легко найти числа, соответствующей каждой поставленной нами на луче точке.

Рис. 5. Луч с отрезками и цифрами

Покажу еще раз на примере точки S :

так как RS=OP (по условиям построения данных отрезков),

подставив известные нам значения длины отрезков OR и OP, получим:

Значит, точке S на нашем лучу соответствует число 3.

Оставим на луче только числовые значения, а все буквы кроме O отбросим. В итоге у нас получился вот такой луч с отрезками и числами, которые соответствуют концам этих отрезков.

Рис. 6. Координатный луч

Глядя на рисунок 6, легко заметить, что отрезки, лежащие на луче, это не что иное, как нанесенная на луч шкала. Действительно, смотрите сами.

Точка O с соответствующим ей числом 0 (нуль) называется точка отсчета, что аналогично нулевой отметке шкалы. Обычно этой буквой всегда помечают в рисунках точку отсчета.

Единичный отрезок – это отрезок, длина которого принята нами за единицу длины и равна 1(единице). Точке, обозначающей правый конец единичного отрезка, соответствует число 1.

Координатный луч – это луч с отмеченным на нем единичным отрезком, точкой начала отсчета, которой соответствует число 0 (нуль), и указанным направлением отсчета.
Координатный луч еще называют числовой луч.

Координатный луч — это не что иное, как бесконечная шкала.

Длина единичного отрезка может быть любой. Она выбирается каждый раз отдельно и при ее выборе ориентируются на то, чтобы на рисунке поместились все необходимые в данный момент числа. Например, на рисунке 7-а длина единичного отрезка составляет 5 см, а на рисунке 7-б всего 1 см.

Рис. 7. Разные варианты единичного отрезка

Как вы заметили из предыдущего рисунка, для разметки луча отрезками можно вместо кружочков использовать штрихи везде, кроме точки O (начала отсчета). Кружочки рисуют поверх этих штрихов тогда, когда необходимо отметить на числовом луче какое-то натуральное число. В этом случае мы дополнительно обозначаем его заглавной (большой) буквой латинского алфавита (смотрите рисунок 8).

Координатный луч служит для наглядного отображения и сравнения чисел натурального ряда.

Действительно, длина каждого отрезка числового луча отличается от длины предыдущего на единицу, точно так же, как и каждый элемент числового ряда отличается от предыдущего.

Координата точки числового луча – это число, которое соответствует поставленной на числовом луче точке.

Рис. 8. Координаты точек

Точке A соответствует число 5 координатного луча, точке B – число 8, точке C – число 13. Запишем полученные координаты точек: A ( 5 ), B ( 8 ), C ( 13 ).

В отдельных случаях для обозначения на координатном луче больших натуральных чисел, допускается не отображать на рисунке точку отсчета и единичный отрезок, показывая только тот участок луча, на котором расположены данные числа.

Рис. 9. Большие числа на координатном луче.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.2 / 5. Количество оценок: 9

Источник