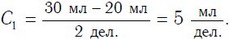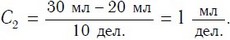Длина деления шкалы

2.8. Длина деления шкалы

По title=»ГСИ. Метрология. Основные термины и определения»

Смотреть что такое «Длина деления шкалы» в других словарях:

длина деления шкалы — Расстояние между осями (или центрами) двух соседних отметок шкалы, измеренное вдоль воображаемой линии, проходящей через середины самых коротких отметок шкалы. [РМГ 29 99] EN scale spacing length of a scale division distance between two… … Справочник технического переводчика

длина деления шкалы — skalės padalos ilgis statusas T sritis Standartizacija ir metrologija apibrėžtis Atstumas tarp dviejų gretimų skalės žymių, išmatuotas išilgai įsivaizduojamos linijos, einančios per trumpiausių žymių centrus. atitikmenys: angl. scale spacing;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

длина деления шкалы — skalės padalos ilgis statusas T sritis Standartizacija ir metrologija apibrėžtis Atstumas tarp dviejų gretimų žymių, išmatuotas išilgai tos pačios linijos kaip ir skalės ilgio atveju. atitikmenys: angl. scale spacing; scale spacing length of a… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

длина деления шкалы — skalės padalos ilgis statusas T sritis fizika atitikmenys: angl. scale spacing vok. Abstand der Teilungsmarken, m; Teilstrichabstand, m rus. длина деления шкалы, f pranc. longueur d’une division d’échelle, f … Fizikos terminų žodynas

длина — 3.1 длина (length) l: Наибольший линейный размер лицевой грани измеряемого образца. Источник: ГОСТ Р ЕН 822 2008: Изделия теплоизоляционные, применяемые в строительстве. Методы измерения длины и ширины … Словарь-справочник терминов нормативно-технической документации

Деления и делительная машина — Для практики наблюдательных наук правильные и точные Д., как линейные, так и угловые, представляют предмет первостепенной важности. Глаз или осязание дает нам лишь возможность судить о равенстве двух промежутков, когда они наложены или надлежащим … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

ДЕЛЕНИЕ ШКАЛЫ — отрезок шкалы между двумя соседними градуировочными отметками на аналоговой шкале. Д. ш. используется как единица счета для выражения показаний. При этом принимается во внимание, что индикаторная метка (указатель) начиная от нулевой отметки… … Энциклопедический словарь по психологии и педагогике

ГОСТ 29329-92: Весы для статического взвешивания. Общие технические требования — Терминология ГОСТ 29329 92: Весы для статического взвешивания. Общие технические требования оригинал документа: (Электронные весы) Термин «Электронные весы» применим к настольным весам Определения термина из разных документов: (Электронные весы)… … Словарь-справочник терминов нормативно-технической документации

Шкала средства измерений — Для термина «Шкала» см. другие значения. Шкала (лат. scala лестница) часть показывающего устройства средства измерений … Википедия

Abstand der Teilungsmarken — skalės padalos ilgis statusas T sritis Standartizacija ir metrologija apibrėžtis Atstumas tarp dviejų gretimų skalės žymių, išmatuotas išilgai įsivaizduojamos linijos, einančios per trumpiausių žymių centrus. atitikmenys: angl. scale spacing;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Источник

ЧИТАТЬ КНИГУ ОНЛАЙН: Метрология, стандартизация и сертификация: конспект лекций

НАСТРОЙКИ.

СОДЕРЖАНИЕ.

СОДЕРЖАНИЕ

А. С. Якорева, В. А. Бисерова, Н. В. Демидова

Метрология, стандартизация и сертификация: конспект лекций

ЛЕКЦИЯ № 1. Метрология

1. Предмет и задачи метрологии

С течением мировой истории человеку приходилось измерять различные вещи, взвешивать продукты, отсчитывать время. Для этой цели понадобилось создать целую систему различных измерений, необходимую для вычисления объема, веса, длины, времени и т. п. Данные подобных измерений помогают освоить количественную характеристику окружающего мира. Крайне важна роль подобных измерений при развитии цивилизации. Сегодня никакая отрасль народного хозяйства не могла бы правильно и продуктивно функционировать без применения своей системы измерений. Ведь именно с помощью этих измерений происходит формирование и управление различными технологическими процессами, а также контролирование качества выпускаемой продукции. Подобные измерения нужны для самых различных потребностей в процессе развития научно—технического прогресса: и для учета материальных ресурсов и планирования, и для нужд внутренней и внешней торговли, и для проверки качества выпускаемой продукции, и для повышения уровня защиты труда любого работающего человека. Несмотря на многообразие природных явлений и продуктов материального мира, для их измерения существует такая же многообразная система измерений, основанных на очень существенном моменте – сравнении полученной величины с другой, ей подобной, которая однажды была принята за единицу. При таком подходе физическая величина расценивается как некоторое число принятых для нее единиц, или, говоря иначе, таким образом получается ее значение. Существует наука, систематизирующая и изучающая подобные единицы измерения, – метрология. Как правило, под метрологией подразумевается наука об измерениях, о существующих средствах и методах, помогающих соблюсти принцип их единства, а также о способах достижения требуемой точности.

Происхождение самого термина «метрология» возводя! к двум греческим словам: metron, что переводится как «мера», и logos – «учение». Бурное развитие метрологии пришлось на конец XX в. Оно неразрывно связано с развитием новых технологий. До этого метрология была лишь описательным научным предметом. Следует отметить и особое участие в создании этой дисциплины Д. И. Менделеева, которому подевалось вплотную заниматься метрологией с 1892 по 1907 гг… когда он руководил этой отраслью российской науки. Таким образом, можно сказать, что метрология изучает:

1) методы и средства для учета продукции по следующим показателям: длине, массе, объему, расходу и мощности;

2) измерения физических величин и технических параметров, а также свойств и состава веществ;

3) измерения для контроля и регулирования технологических процессов.

Выделяют несколько основных направлений метрологии:

1) общая теория измерений;

2) системы единиц физических величин;

3) методы и средства измерений;

4) методы определения точности измерений;

5) основы обеспечения единства измерений, а также основы единообразия средств измерения;

6) эталоны и образцовые средства измерений;

7) методы передачи размеров единиц от образцов средств измерения и от эталонов рабочим средствам измерения. Важным понятием в науке метрологии является единство измерений, под которым подразумевают такие измерения при которых итоговые данные получаются в узаконенных единицах, в то время как погрешности данных измерений получены с заданной вероятностью. Необходимость существования единства измерений вызвана возможностью сопоставления результатов различных измерений, которые были проведены в различных районах, в различные временные отрезки, а также с применением разнообразных методов и средств измерения.

Следует различать также объекты метрологии:

1) единицы измерения величин;

2) средства измерений;

3) методики, используемые для выполнения измерений и т. д.

Метрология включает в себя: во—первых, общие правила, нормы и требования, во—вторых, вопросы, нуждающиеся в государственном регламентировании и контроле. И здесь речь идет о:

1) физических величинах, их единицах, а также об их измерениях;

2) принципах и методах измерений и о средствах измерительной техники;

3) погрешностях средств измерений, методах и средствах обработки результатов измерений с целью исключения погрешностей;

4) обеспечении единства измерений, эталонах, образцах;

5) государственной метрологической службе;

6) методике поверочных схем;

7) рабочих средствах измерений.

В связи с этим задачами метрологии становятся: усовершенствование эталонов, разработка новых методов точных измерений, обеспечение единства и необходимой точности измерений.

Очень важным фактором правильного понимания дисциплины и науки метрология служат использующиеся в ней термины и понятия. Надо сказать, что, их правильная формулировка и толкование имеют первостепенное значение, так как восприятие каждого человека индивидуально и многие, даже общепринятые термины, понятия и определения он трактует по—своему, используя свой жизненный опыт и следуя своим инстинктам, своему жизненному кредо. А для метрологии очень важно толковать термины однозначно для всех, поскольку такой подход дает возможность оптимально и целиком понимать какое— либо жизненное явление. Для этого был создан специальный стандарт на терминологию, утвержденный на государственном уровне. Поскольку Россия на сегодняшний момент воспринимает себя частью мировой экономической системы, постоянно идет работа над унификацией терминов и понятий, создается международный стандарт. Это, безусловно, помогает облегчить процесс взаимовыгодного сотрудничества с высокоразвитыми зарубежными странами и партнерами. Итак, в метро логии используются следующие величины и их определения:

1) физическая величина, представляющая собой общее свойство в отношении качества большого количества физических объектов, но индивидуальное для каждого в смысле количественного выражения;

2) единица физической величины, что подразумевает под собой физическую величину, которой по условию присвоено числовое значение, равное единице;

3) измерение физических величин, под которым имеется в виду количественная и качественная оценка физического объекта с помощью средств измерения;

4) средство измерения, представляющее собой техническое средство, имеющее нормированные метрологические характеристики. К ним относятся измерительный прибор, мера, измерительная система, измерительный преобразователь, совокупность измерительных систем;

5) измерительный прибор представляет собой средство измерений, вырабатывающее информационный сигнал в такой форме, которая была бы понятна для непосредственного восприятия наблюдателем;

6) мера – также средство измерений, воспроизводящее физическую величину заданного размера. Например, если прибор аттестован как средство измерений, его шкала с оцифрованными отметками является мерой;

7) измерительная система, воспринимаемая как совокупность средств измерений, которые соединяются друг с другом посредством каналов передачи информации для выполнения одной или нескольких функций;

8) измерительный преобразователь – также средство измерений, которое производит информационный измерительный сигнал в форме, удобной для хранения, просмотра и трансляции по каналам связи, но не доступной для непосредственного восприятия;

9) принцип измерений как совокупность физических явлений, на которых базируются

Источник

Шкала измерительного прибора, цена деления шкалы

Шкала — плоская или цилиндрическая поверхность, относительно которой движется стрелка, на которой нанесены деления.

Иногда шкала у прибора всего одна, а иногда их несколько, при этом индикатором измерений служит всего одна стрелка. Давайте же разберемся, что это за шкалы, и как ими пользоваться, чтобы ничего не напутать.

Для начала отметим, что шкалы эти бывают разными. Во-первых, более распространенными являются именованные шкалы, то есть шкалы, на которых деления проградуированы соответствующими единицами измеряемых величин, это градуированные шкалы.

Во-вторых, встречаются условные шкалы. Если прибор имеет несколько переключаемых пределов измерений, то шкала будет наверняка условной, и одни и те же деления будут иметь разные значения в каждом из установленных пользователем пределов.

Для того, чтобы по условной шкале прибора определить точно значение измеряемой в данный момент величины, необходимо, зная цену деления, количество делений до того места, куда отклонилась, и где остановилась в данный момент стрелка, умножить на цену деления.

Если цена деления не ясна, то ее можно легко найти, для этого берется разность между двумя известными значениями на шкале, и делится на количество делений между этими значениями. Например, известно, что красная шкала имеет ширину 10 вольт, а количество делений 50, значит цена деления для красной шкалы составляет 200 мВ.

Если на шкале есть отметка ноль, то шкала называется нулевой. Если нуля нет, то шкала называется безнулевой. Что касается нулевых шкал, то они, в свою очередь, подразделяются на односторонние и двухсторонние. На фото выше можно видеть сразу семь нулевых шкал.

У односторонних ноль размещен в самом начале шкалы (как на рисунке, головка вольтметра с односторонней шкалой), а у двухсторонних — по центру или между конечной и начальной отметками. Так, в зависимости от расположения нуля, двухсторонние шкалы подразделяются на несимметричные и симметричные.

Симметричная шкала ноль имеет по центру, несимметричная — не по центру шкалы. Если шкала безнулевая, то крайние отметки обозначают верхний и нижний пределы измерений. На фото выше изображен миллиамперметр с симметричной двухсторонней шкалой, цена деления составляет 50 мкА, поскольку 0,5 мА / 10 = 0,05 мА или 50 мкА.

В зависимости от характера связи угловых и линейных расстояний между двумя соседними делениями шкалы с измеряемыми величинами, шкалы бывают неравномерными, равномерными, логарифмическими, степенными и т. д. Для более точных измерений предпочтительней равномерные шкалы.

Когда отношение ширины самого широкого деления к самому узкому не более 1,3 при неизменной цене деления, шкалу уже можно считать равномерной.

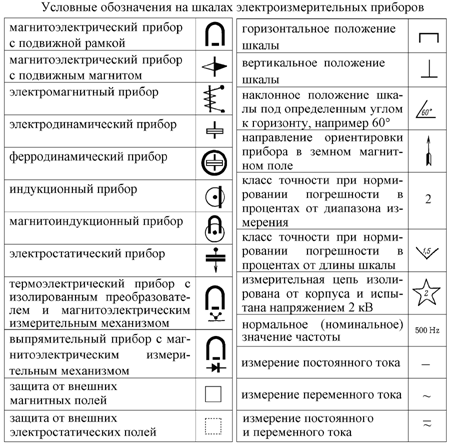
На лицевой стороне измерительного прибора, недалеко от шкалы, как правило, размещены необходимые маркировки: единица величины измерения, ГОСТ, класс точности прибора, число фаз и род тока, категория защищенности данного измерительного прибора от внешних электрических и магнитных полей, условия эксплуатации, рабочее положение, предельное напряжение прочности изоляции измерительных цепей (на фото — в звездочке «2», значит 2 кВ), номинальная частота тока, если отличается от промышленных 50 Гц, например 500 Гц, положение относительно Земли, тип, система прибора, год выпуска, заводской номер, и прочие важные параметры.

В этой таблице приведены расшифровки основных обозначений, которые можно встретить на шкалах. Надеемся, что эта краткая статья поможет вам научиться правильно проводить измерения при помощи стрелочных измерительных приборов.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Шкалы, координаты

Для определения размера какой-либо величины (длина, вес, температура и т.д.) мы используем измерительные приборы и инструменты со шкалами для отображения результата.

Шкала – это расположенный в определенной последовательности ряд отметок, которые соответствуют числовому значению измеряемой величины.

Например, в школьном курсе математики и геометрии для измерения длины геометрического объекта, в частности отрезка, используется линейка (рисунок 1).

Рисунок 1. Измерительная линейка.

Из урока Измерение величин вы уже знаете, что такое единица измерения, а их соотношения можете посмотреть в справочном разделе.

Деления шкалы – это равные части, на которые она разбита. Каждое деление шкалы обозначается отметками (черточками).

Нулевая отметка шкалы – это отметка, которая соответствует нулевому значению измеряемой нами величины.

Цена деления шкалы – это величина значения одного деления шкалы. То есть, это величина значения между двумя соседними отметками на шкале.

Как мы видим на рисунке 1, деления, обозначенные большими черточками, пронумерованы, и значение каждого такого деления равно 1 см. В этом легко убедиться, если найти разницу между значениями каждого из соседних делений: 1-0=1, 2-1=3, …, 9-8=1, 10-9=1.
Но каждое из больших делений разделено девятью маленькими черточками на 10 делений. Мы знаем, что в 1 см содержится 10 мм, поэтому разделив эти 10 мм на 10 делений, мы получим цену деления линейки, равную 1 мм.

Цена деления может отличаться не только у разных же измерительных приборов, но и у одних и тех же.

Рисунок 2 Цена деления шкалы

Например, на рисунке 2 изображены два термометра. Как вы думаете, они показывают одинаковую температуру, или нет?

Давайте посмотрим, так ли это? На левом термометре разница между двумя соседними пронумерованными отметками равна 10°C: 10-0=10, 20-10=10, и т.д. На правом же термометре эта разница равняется уже 20°C: 20-0=20, 40-20=20, и т.д. На обоих термометрах маленькие черточки делят одно большое пронумерованное деление на 10 частей. Разделив разницу между значениями пронумерованных отметок (10 и 20 соответственно) на количество делений между ними (10), мы получим цену деления каждого из термометров:

Итак, оба термометра показывают 20°C и еще два деления. Но на левом термометре это означает 20°C и еще два раза по 1°C, то есть, 20+2=22°C, а на правом – 20°C и еще два раза по 2°C, то есть, 20+4=24°C.

Координатный луч, единичный отрезок, координаты точки

Различные прямые линии со шкалами играют важную роль в школьной математике. Сейчас я познакомлю вас с одной из них.

Нарисуем точку O и проведем от нее направо луч. Обозначим направление луча стрелкой.

Рис. 3. Луч с началом в точке O

Рис. 4. Луч с равными отрезками

Поставим возле начала луча (точки O ) число 0 (нуль). Возле второго конца отрезка OP (возле точки P ) поставим число 1 (один). Таким образом мы обозначаем, что длина отрезка OP равна 1 (единице).

Аналогичным образом вы можете легко найти числа, соответствующей каждой поставленной нами на луче точке.

Рис. 5. Луч с отрезками и цифрами

Покажу еще раз на примере точки S :

так как RS=OP (по условиям построения данных отрезков),

подставив известные нам значения длины отрезков OR и OP, получим:

Значит, точке S на нашем лучу соответствует число 3.

Оставим на луче только числовые значения, а все буквы кроме O отбросим. В итоге у нас получился вот такой луч с отрезками и числами, которые соответствуют концам этих отрезков.

Рис. 6. Координатный луч

Глядя на рисунок 6, легко заметить, что отрезки, лежащие на луче, это не что иное, как нанесенная на луч шкала. Действительно, смотрите сами.

Точка O с соответствующим ей числом 0 (нуль) называется точка отсчета, что аналогично нулевой отметке шкалы. Обычно этой буквой всегда помечают в рисунках точку отсчета.

Единичный отрезок – это отрезок, длина которого принята нами за единицу длины и равна 1(единице). Точке, обозначающей правый конец единичного отрезка, соответствует число 1.

Координатный луч – это луч с отмеченным на нем единичным отрезком, точкой начала отсчета, которой соответствует число 0 (нуль), и указанным направлением отсчета.
Координатный луч еще называют числовой луч.

Координатный луч — это не что иное, как бесконечная шкала.

Длина единичного отрезка может быть любой. Она выбирается каждый раз отдельно и при ее выборе ориентируются на то, чтобы на рисунке поместились все необходимые в данный момент числа. Например, на рисунке 7-а длина единичного отрезка составляет 5 см, а на рисунке 7-б всего 1 см.

Рис. 7. Разные варианты единичного отрезка

Как вы заметили из предыдущего рисунка, для разметки луча отрезками можно вместо кружочков использовать штрихи везде, кроме точки O (начала отсчета). Кружочки рисуют поверх этих штрихов тогда, когда необходимо отметить на числовом луче какое-то натуральное число. В этом случае мы дополнительно обозначаем его заглавной (большой) буквой латинского алфавита (смотрите рисунок 8).

Координатный луч служит для наглядного отображения и сравнения чисел натурального ряда.

Действительно, длина каждого отрезка числового луча отличается от длины предыдущего на единицу, точно так же, как и каждый элемент числового ряда отличается от предыдущего.

Координата точки числового луча – это число, которое соответствует поставленной на числовом луче точке.

Рис. 8. Координаты точек

Точке A соответствует число 5 координатного луча, точке B – число 8, точке C – число 13. Запишем полученные координаты точек: A ( 5 ), B ( 8 ), C ( 13 ).

В отдельных случаях для обозначения на координатном луче больших натуральных чисел, допускается не отображать на рисунке точку отсчета и единичный отрезок, показывая только тот участок луча, на котором расположены данные числа.

Рис. 9. Большие числа на координатном луче.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.2 / 5. Количество оценок: 9

Источник

§ 7. Измерительные приборы. Цена деления. Точность измерений

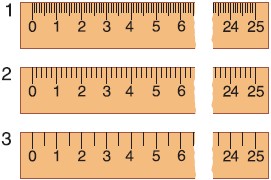
На рисунке 39 изображены три линейки с одинаковыми верхними пределами (25 см). Но эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 1, менее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала цену деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.

Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.

C₁ = 1 см : 10 дел = 0,1 см/дел

C₂ = 1 см : 5 дел = 0,2 см/дел

C₃ = 1 см : 2 дел = 0,5 см/дел

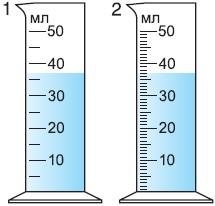
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 40). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2:

Измерим один и тот же объем мензуркой 1 и мензуркой 2. Исходя из показаний шкалы объем воды в мензурке 1:

V = 35 мл.

Из показаний шкалы мензурки 2:

V = 37 мл.

Понятно, что точнее измерен объем воды мензуркой 2, цена де- ления которой меньше (1 мл/дел

Источник