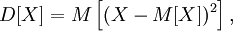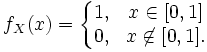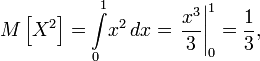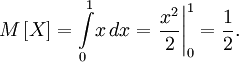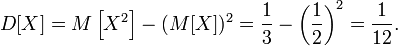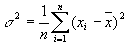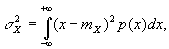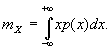Что такое дисперсия в метрологии
Дисперсия измерений
Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, т. е. её отклонения от математического ожидания. Обозначается D[X] в русской литературе и 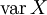
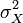
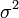
Содержание
Определение
Пусть 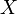
Замечания
Свойства дисперсии
Пример
Пусть случайная величина 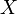
См. также
Полезное
Смотреть что такое «Дисперсия измерений» в других словарях:
ДИСПЕРСИЯ — (variance) Мера разброса данных. Дисперсия множества из N членов находится путем сложения квадратов их отклонений от среднего значения и деления на N. Поэтому, если членами являются хi при i = 1, 2. N, a их средним является m, дисперсия… … Экономический словарь
Дисперсия — * дысперсія * dispersion 1. Рассеяние; разброс; вариация (см.). 2. Теоретико вероятностное понятие, характеризующее меру отклонения случайной величины от ее математического ожидания. В биометрической практике используется выборочная дисперсия s2 … Генетика. Энциклопедический словарь
дисперсия — 2.25 дисперсия: Среднее значение квадратов отклонения случайной переменной от ее среднего, которое оценивают по среднему квадрату. Источник … Словарь-справочник терминов нормативно-технической документации
дисперсия (случайной переменной величины или распределения вероятностей) — 3.21 дисперсия (случайной переменной величины или распределения вероятностей) (variance): Центральный момент 2 го порядка. Примечание Дисперсия случайной переменной величины может быть также определена как математическое ожидание квадрата… … Словарь-справочник терминов нормативно-технической документации
Дисперсия звука — зависимость фазовой скорости монохроматических звуковых волн от частоты. Д. з. является причиной изменения формы звуковой волны (звукового импульса) при распространении его в среде. Различают Д. з., обусловленную физическими свойствами… … Большая советская энциклопедия
ДИСПЕРСИЯ — (от лат. dispersus рассеянный, рассыпанный) стат. величина, характеризующая степень разброса количественных измерений индивидуальных участников статистической выборки (случайных величин) относительно среднего значения для этой выборки … Профессиональное образование. Словарь
дисперсия — величина, характеризующая степень разброса количественных измерений индивидуальных участников статистической выборки (случайных величин) относительно среднего значения для этой выборки … Словарь экономических терминов
ГОСТ Р 8.580-2001: Государственная система обеспечения единства измерений. Определение и применение показателей прецизионности методов испытаний нефтепродуктов — Терминология ГОСТ Р 8.580 2001: Государственная система обеспечения единства измерений. Определение и применение показателей прецизионности методов испытаний нефтепродуктов оригинал документа: 2.19.1 воспроизводимость результатов испытаний:… … Словарь-справочник терминов нормативно-технической документации
ГОСТ Р ИСО 11222-2006: Качество воздуха. Оценка неопределенности измерений характеристик качества воздуха, полученных усреднением по времени — Терминология ГОСТ Р ИСО 11222 2006: Качество воздуха. Оценка неопределенности измерений характеристик качества воздуха, полученных усреднением по времени оригинал документа: 3.6 влияющая величина (influence quantity): Величина, не являющаяся… … Словарь-справочник терминов нормативно-технической документации
Дисперсия
Полезное
Смотреть что такое «Дисперсия» в других словарях:
дисперсия — Рассеяние чего нибудь. В математике дисперсия определяет отклонение величин от среднего значения. Дисперсия белого света приводит к его разложению на составляющие. Дисперсия звука является причиной его расплывания. Рассеяние хранимых данных по… … Справочник технического переводчика
ДИСПЕРСИЯ — (от латинского dispersio рассеяние) волн, зависимость скорости распространения волн в веществе от длины волны (частоты). Дисперсия определяется физическими свойствами той среды, в которой распространяются волны. Например, в вакууме… … Современная энциклопедия
ДИСПЕРСИЯ — (variance) Мера разброса данных. Дисперсия множества из N членов находится путем сложения квадратов их отклонений от среднего значения и деления на N. Поэтому, если членами являются хi при i = 1, 2. N, a их средним является m, дисперсия… … Экономический словарь
Дисперсия — (от латинского dispersio рассеяние) волн, зависимость скорости распространения волн в веществе от длины волны (частоты). Дисперсия определяется физическими свойствами той среды, в которой распространяются волны. Например, в вакууме… … Иллюстрированный энциклопедический словарь
ДИСПЕРСИЯ — (от лат. dispersio рассеяние) в математической статистике и теории вероятностей мера рассеивания (отклонения от среднего). В статистике дисперсия есть среднее арифметическое из квадратов отклонений наблюденных значений (x1, x2. xn) случайной… … Большой Энциклопедический словарь
Дисперсия — в теории вероятностей наиболее употребительная мера отклонения от среднего (мера рассеяния). По английски: Dispersion Синонимы: Статистическая дисперсия Синонимы английские: Statistical dispersion См. также: Выборочные совокупности Финансовый… … Финансовый словарь
ДИСПЕРСИЯ — [лат. dispersus рассеянный, рассыпанный] 1) рассеяние; 2) хим., физ. раздробление вещества на очень малые частицы. Д. света разложение белого света с помощью призмы в спектр; 3) мат. отклонение от среднего. Словарь иностранных слов. Комлев Н.Г.,… … Словарь иностранных слов русского языка
дисперсия — (варианса) показатель разброса данных, соответственный среднему квадрату отклонения этих данных от средней арифметической. Равна квадрату стандартного отклонения. Словарь практического психолога. М.: АСТ, Харвест. С. Ю. Головин. 1998 … Большая психологическая энциклопедия
дисперсия — рассеяние, разброс Словарь русских синонимов. дисперсия сущ., кол во синонимов: 6 • нанодисперсия (1) • … Словарь синонимов
Дисперсия — [variance] характеристика рассеивания значений случайной величины, измеряемая квадратом их отклонений от среднего значения (обозначается d2). Различается Д. теоретического (непрерывного или дискретного) и эмпирического (также непрерывного и… … Экономико-математический словарь
Дисперсия — * дысперсія * dispersion 1. Рассеяние; разброс; вариация (см.). 2. Теоретико вероятностное понятие, характеризующее меру отклонения случайной величины от ее математического ожидания. В биометрической практике используется выборочная дисперсия s2 … Генетика. Энциклопедический словарь
Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Расчет дисперсии в Excel
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Стандартное отклонение
Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.
Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.
Стандартное отклонение обозначается буквой σ (греческая буква сигма).
Стандартное отклонение также называется:
Использование и интерпретация величины среднеквадратического отклонения
Стандартное отклонение используется:
Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.
| День 1 | День 2 | День 3 | День 4 | |
|---|---|---|---|---|
| Пред.А | 19 | 21 | 19 | 21 |
| Пред.Б | 15 | 26 | 15 | 24 |
В обеих компаниях среднее количество товара составляет 20 единиц:
Однако, глядя на цифры, можно заметить:
Если рассчитать стандартное отклонение каждой компании, оно покажет, что
Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения
Разница между формулами S и σ («n» и «n–1»)
Состоит в том, что мы анализируем — всю выборку или только её часть:
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:
Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
3. Каждую полученную разницу возвести в квадрат:
4. Сделать сумму полученных значений:
5. Поделить на размер выборки (т.е. на n):
6. Найти квадратный корень:
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Дисперсия и стандартное отклонение
Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).
Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:
Ещё расчёт дисперсии можно сделать по этой формуле:
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.
Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Стандартное отклонение в excel
Вычисление стандартного отклонения с «n – 1» в знаменателе (случай выборки из генеральной совокупности):
1. Занесите все данные в документ Excel.
2. Выберите поле, в котором вы хотите отобразить результат.
3. Введите в этом поле «=СТАНДОТКЛОНА(«
4. Выделите поля, где находятся данные, потом закройте скобки.
5. Нажмите Ввод (Enter).
В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.
Коэффициент вариации
Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.
Стандартное отклонение делится на среднее и умножается на 100%.
Можно классифицировать вариабельность выборки по коэффициенту вариации:
ДИСПЕРСИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
DX=E(X-EX) 2 =
DX = 
2. Если X — случайная величина, распределенная по нормальному закону с плотностью
f(x) =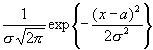
где а, σ — параметры распределения, то Д. с. в. в этом случае равна:
DX =
(см. Плотность распределения вероятностен). Выборочные оценки Д. с. в. широко используются во всех геол. дисциплинах, опирающихся па количественные характеристики. Аналогами Д. с. в. являются распространенные в литологии коэффициенты сортировки.
Полезное
Смотреть что такое «ДИСПЕРСИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ» в других словарях:
Дисперсия случайной величины — У этого термина существуют и другие значения, см. Дисперсия. Дисперсия случайной величины мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается в русской литературе и (англ. variance)… … Википедия
дисперсия (случайной величины) — 1.22. дисперсия (случайной величины) Математическое ожидание квадрата центрированной случайной величины Источник: ГОСТ Р 50779.10 2000: Статистические методы. Вероятн … Словарь-справочник терминов нормативно-технической документации
Дисперсия случайной величины — 1.18. Дисперсия случайной величины s2 s2= E [(X E(X))2] Источник: ГОСТ 15895 77: Статистические методы управления качеством продукции. Термины и определения … Словарь-справочник терминов нормативно-технической документации
дисперсия (случайной переменной величины или распределения вероятностей) — 3.21 дисперсия (случайной переменной величины или распределения вероятностей) (variance): Центральный момент 2 го порядка. Примечание Дисперсия случайной переменной величины может быть также определена как математическое ожидание квадрата… … Словарь-справочник терминов нормативно-технической документации
Моменты случайной величины — Момент случайной величины числовая характеристика распределения данной случайной величины. Содержание 1 Определения 2 Замечания … Википедия
ДИСПЕРСИЯ — (от лат. dispersio рассеяние) в математической статистике и теории вероятностей мера рассеивания (отклонения от среднего). В статистике дисперсия есть среднее арифметическое из квадратов отклонений наблюденных значений (x1, x2. xn) случайной… … Большой Энциклопедический словарь
дисперсия — 2.25 дисперсия: Среднее значение квадратов отклонения случайной переменной от ее среднего, которое оценивают по среднему квадрату. Источник … Словарь-справочник терминов нормативно-технической документации